结构力学位移法实验教学装置开发及教学实践

江守燕， 金 蓉， 杨海霞， 孙立国

（1.河海大学力学与工程科学学院，南京 211100；2.大连海事大学交通运输工程学院，辽宁 大连 116026）

0 引 言

结构力学是力学、土木、港航等专业本科生的主要学科基础课程之一，本课程的任务是在理论力学和材料力学等课程的基础上进一步掌握平面杆件结构分析的基本概念、基本原理和基本方法，了解各类结构的力学性能，为学习有关专业课程以及进行结构设计和科学研究打好力学基础，培养学生结构分析与计算等方面的能力，这门课程是力学理论与工程实践紧密联系的桥梁和纽带。

力法和位移法是求解超静定结构的2 种经典方法，也是结构力学教学中的重点和难点内容。力法的重点是“力”，关于力的分析方法在静定结构的计算中学生已经比较熟悉；位移法的重点是“位移”，根据变形位移确定内力的分析方法对学生来说属于比较新的和陌生的知识。位移法的基本思路、基本系和基本未知量的确定等都比力法难以理解，是结构力学最重要和最难理解的内容［1］。位移法基本系高度抽象，不但可以说是“无中生有”，而且结点位移和荷载分别单独作用于基本系的状态与原有结构中荷载引起内力和变形（包括节点位移）的概念相冲突。由于位移法的“难”，导致很多学生在没有理解位移法基本原理的情况下，难以基于位移法的基本原理进行结构的概念分析［2］。然而，结构分析的核心概念和方法是教学过程中应该着重强调的［3-5］，而不应该仅仅强调求解问题的技巧。朱少云［6］探讨了建立位移法方程的2 种方式，即典型方程法和平衡方程法，并讨论了位移法典型方程的取舍对结构力学教学的影响；崔玉红等［7］指出，经典的位移法规律是一次加约束和一次拆约束的计算过程；杨迪雄［8］系统介绍了位移法的发展历程及对结构现代发展所起的作用；田振国［9］对比了超静定结构求解的几种方法，包括力法、位移法、力矩分配法等，对几种方法的理论基础、未知量、特点、适用条件和适用问题等进行了探讨。

结构力学是一门与工程实际紧密联系的课程，但在结构力学理论教学中，存在不见“结构”的问题［10-11］。实践教学环节在理工科课程教学中的重要性已成共识，并已成为教学体系的重要环节［12-15］。尽管结构力学课程教学基本要求中没有实验要求，但是河海大学结构力学课程结合人才培养的实际需要，于2003 年在国内率先开设结构静、动力学实验，通过实验教学和课外实践活动，激发学生的学习兴趣，提高学生动手能力和研究问题能力。实验室还为学生创新实践提供场地和条件，通过举办和参加各类力学和结构设计竞赛、指导大学生课外创新实践等活动，培养富有创新精神和具有创新能力的人才。在近来的结构力学教学中，又研制了结构力学位移法基本原理的演示装置和实验装置，将课堂理论教学与实验教学有机融合。

1 位移法基本原理演示装置

固定支座、铰支座、滑移支座是结构力学中3 种常见的支座类型，为了直观地展示这3 种支座形式以及不同支座对杆件变形的限制作用，设计并加工了2 种超静定刚架，一种为三端固定的超静定三杆刚架（见图1），另一种为考虑不同支座形式的超静定三杆刚架（见图2）。演示装置的主要部件包括刚臂、刚臂转动顶推装置、加载装置以及刚臂锁定旋钮。杆件的材质为橡胶棒，杆截面为方形，截面尺寸为2 cm ×2 cm。在荷载作用下杆件能够呈现肉眼可见的变形，加深学生对杆件变形规律的认知。该装置已用于课堂实验教学（见图3），可分别演示位移法原结构和基本系的变形过程。

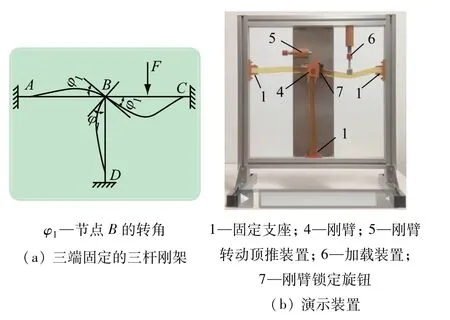
图1 三端固定的三杆刚架及演示装置

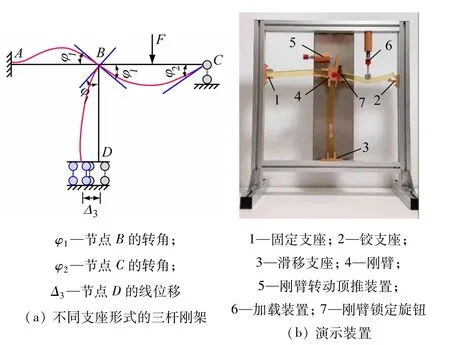
图2 不同支座形式的三杆刚架及演示装置

图3 演示装置用于课堂教学

原结构变形演示过程包括以下步骤：①旋转刚臂转动顶推装置的旋钮，使得刚臂转动顶推装置远离刚臂；②旋转刚臂锁定旋钮，使其处于“放松”状态；③通过旋转加载装置上的旋钮，在BC端杆上施加荷载F。学生可直观地看到由施加在BC端杆上的荷载所引起的杆件变形，BC端杆的变形带动刚节点B的转动，在刚节点B转动过程中，与刚节点B相连的BA端杆以及BC端杆也同步发生变形，加载结束后的最终变形如图1（a）所示。在原结构中“转动”和“荷载”同时存在，无法分离。

基本系变形演示过程包括以下步骤：①旋转加载装置上的旋钮，使其处于“卸荷”状态；②旋转刚臂锁定旋钮，使其处于“放松”状态；③旋转刚臂转动顶推装置的旋钮，顶推刚臂发生转动，当刚臂转动到φ1时，旋转刚臂锁定旋钮，锁定刚臂，刚臂便不再转动；④旋转加载装置上的旋钮，在BC端杆上施加荷载，可以观察到荷载只引起BC端杆的变形，刚节点B不再转动。通过这样一个演示过程，展示位移法基本系可以仅有转动，也可以仅有荷载，还可以先有转动再有荷载，基本系中可以把引起结构变形的原因——“荷载”和“节点转动”分开来考虑。

研制的演示装置可以定性地展示结构的变形状态，辅助位移法基本原理的讲解，让学生可以看到“结构”，看到“结构变形”，看到“刚臂”，看到“基本系”及其在外荷载和节点位移单独作用下的2 个状态，将抽象的位移法基本系形象化、直观化。

2 位移法基本原理实验装置

研制的位移法基本原理演示装置可以定性、直观地展示结构的变形，但无法定量地给出结构的变形、内力数值，为此还研制了与演示装置相配套的实验装置［16］。该实验可以加深学生对结构力学位移法概念及求解方法的理解，实验中还涉及半桥自补偿的电阻应变测试技术，有利于提高学生对电测法的应用能力，在应变与弯矩转化方法的应用上又涉及材料力学。

如图4 所示，该实验装置可以精确地测试结构变形、内力。与1 节中演示装置不同，该实验装置增加了百分表，测量刚臂转角。刚臂顶部外伸段与百分表相连，如图4（b）所示。刚臂顶部外伸段长度Lc=70mm，百分表示数为Di，刚臂实际转角φ1可通过下式计算：

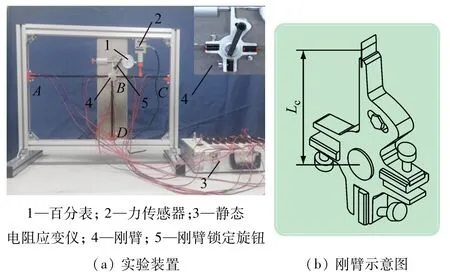
图4 位移法基本原理实验装置

加载装置与力传感器相连可测得所施加荷载的大小。通过变换支座形式，可组装成不同的结构形式。杆件截面为矩形，材质为有机玻璃或弹簧钢（无肉眼可见的变形）。杆件上粘贴了若干应变片，通过静态电阻应变仪测量各杆端应变ε，可通过下式计算每根杆件的杆端弯矩

式中：E为杆件的弹性模量；b为矩形杆件截面的宽度；h为截面的高度。在实验过程中，可通过该实验装置再现原结构和基本系的变形过程，并测出具体数值。将原结构的变形和内力数值与基本系的变形和内力数值进行比较，理论上原结构和基本系的内力和变形应该完全一致，但实验测试时会存在误差，学生可以从中分析误差产生的原因。

具体的实验步骤包括：

（1）测量杆件的弹性模量E，各杆件的有效长度lBA、lBC和lBD，杆件截面的宽度b和高度h。以如图1（a）所示的三端固定超静定刚架为例，杆件材质为有机玻璃，杆件的弹性模量E=3.35 GPa，杆件的有效长度lBA=32 cm、lBC=lBD=20 cm，杆件截面的宽度b=12 mm、高度h=8 mm。

（2）旋转刚臂锁定旋钮，“放松”刚臂。通过加载装置施加竖向集中荷载作用于BC端杆上，荷载F通过力显示器读出，这里取F=6 N（本实验装置可供学生在5 ～10 N范围内自主施加荷载大小）。读取此时D1，通过静态电阻应变仪，测出原结构的杆端应变εAB1、εBA1、εBC1、εCB1、εBD1、εDB1。通过式（2）计算出每根杆件的杆端弯矩MAB1、MBA1、MBC1、MCB1、MBD1、MDB1，相关数据填入实验记录表（见表1）中，并画出原结构在集中荷载下的弯矩图。

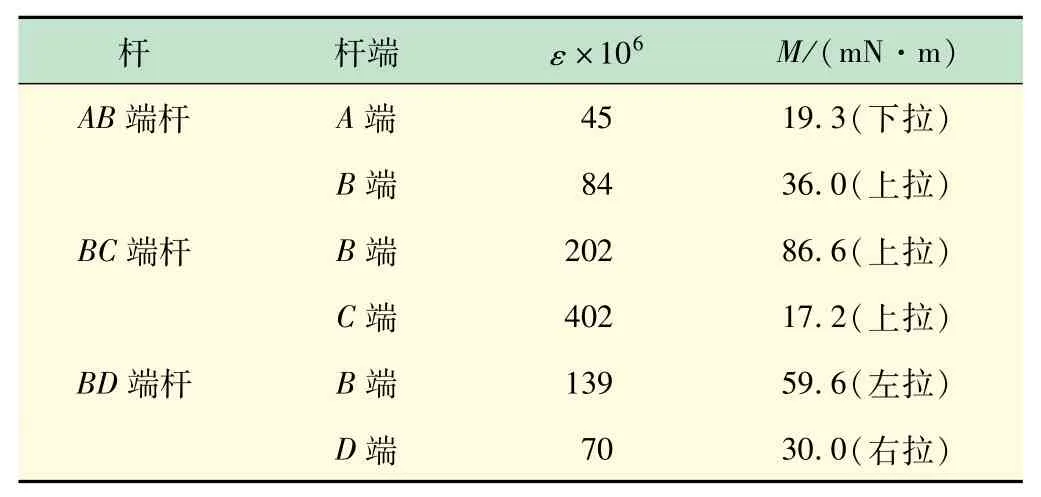
表1 原结构各杆端应变和弯矩

（3）旋转刚臂锁定旋钮，“放松”刚臂，然后旋转刚臂转动顶推装置的旋钮，顶推刚臂发生转角φ1，即使百分表指针指到步骤（2）的示数D1。通过静态电阻应变仪测量各杆端应变根据测得的各杆端应变，通过式（2）计算出每根杆件的杆端弯矩，相关数据填入实验记录表（见表2）中，并画出弯矩图。

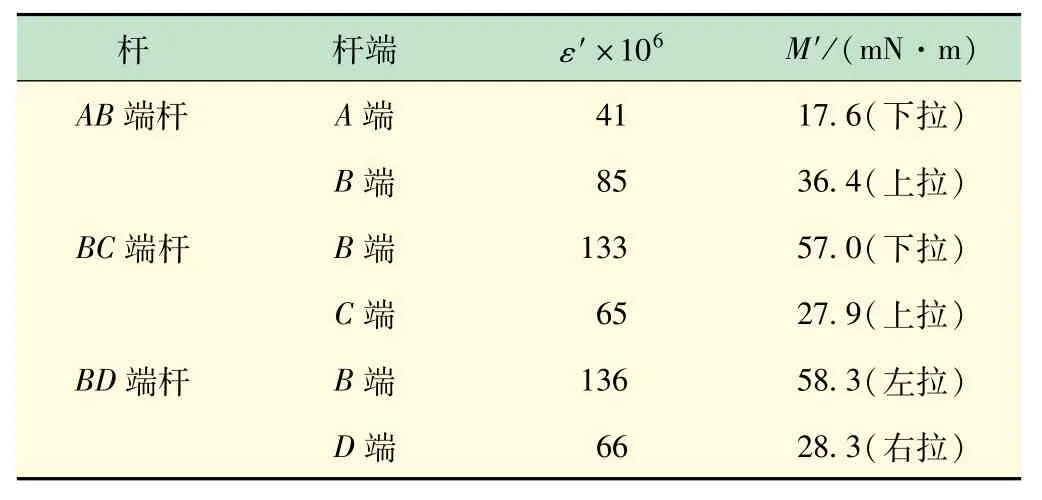
表2 节点位移单独作用下各杆端应变和弯矩

（4）旋转刚臂转动顶推装置的旋钮，使刚节点B转角归零，然后旋转刚臂锁定旋钮，“锁定”刚臂，施加与步骤（2）相同的竖向集中荷载，如F=6 N。通过静态电阻应变仪，测出杆件的杆端应变。根据式（2）计算出每根杆件的杆端弯矩，相关数据填入实验记录表（见表3）中，并画出弯矩图。

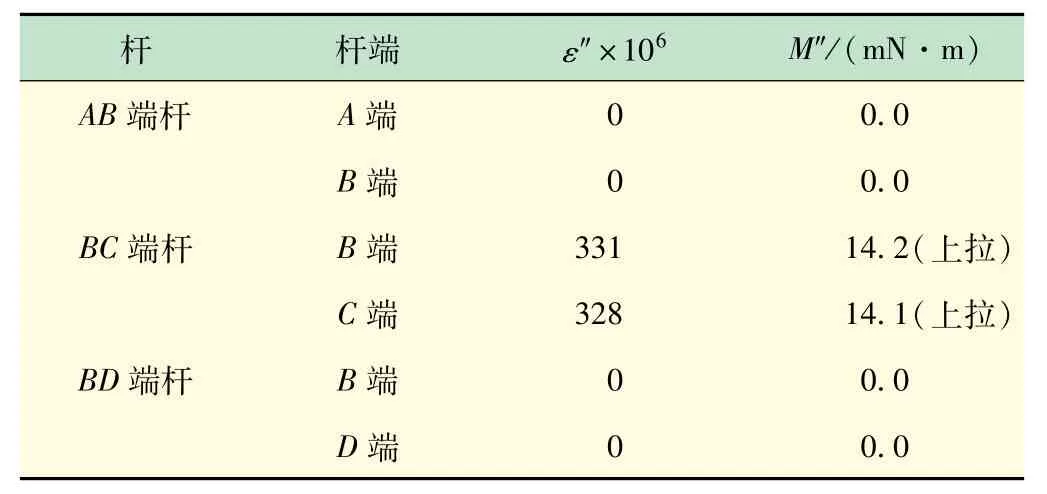
表3 外荷载单独作用下各杆端应变和弯矩

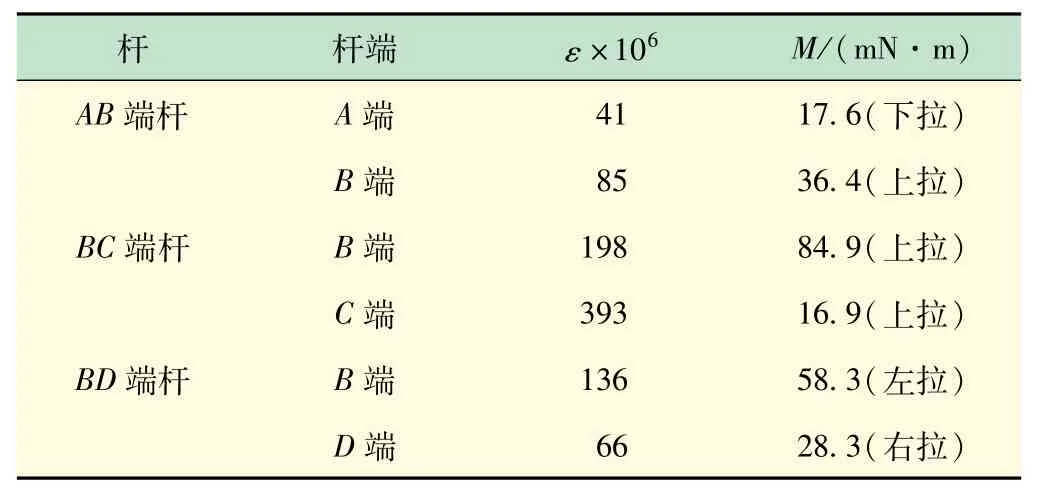
表4 基本系各杆端应变和弯矩

（6）比较步骤（2）、（5）所得的杆端应变和弯矩，分析实验结果并撰写实验报告。

3 位移法基本原理教学设计

位移法基本原理是结构力学课程的重点，也是最难点，概念抽象。结合研制的演示装置和实验装置，采用课堂讲授、问题探讨、动画演示以及装置演示的方式加深学生对该知识点的理解。

以如图5（a）所示的超静定三杆刚架为例，该刚架为6 次超静定结构，采用力法计算时可以取如图5（b）所示的基本系，含有6 个基本未知量F1，F2，…，F6。对于高次超静定结构，采用力法计算时基本未知量多，方程求解繁琐，因此有必要寻找新的计算方法，即位移法。位移法的概念和思想不仅适用于杆件结构的分析，还可以推广到实体结构，是现代计算力学分析方法——有限元法的基础。

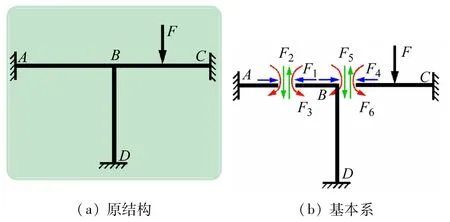
图5 力法计算高次超静定结构

3.1 位移法基本思路

仍以三杆刚架为例，在不计杆件轴向变形的情况下，刚节点B只有角位移而没有线位移，根据位移协调条件，与B点相连的BA端杆、BC端杆以及BD端杆的刚节点B转角相等，都是φ1。在课堂上讨论原超静定刚架结构在荷载作用下与单跨梁在杆端位移和外荷载共同作用下内力和变形状态的联系，如图6 所示。

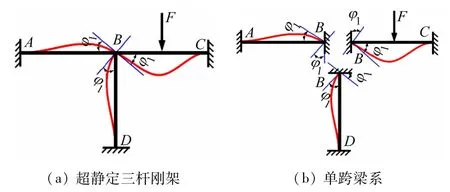
图6 超静定三杆刚架及对应的单跨梁系

若刚节点B的转角φ1求出，则各个杆件的内力能够求出吗？这时原超静定刚架可以看作单跨超静定梁系受杆端位移和杆上荷载共同作用。如果φ1已知，单跨梁的杆端内力就可以用已经学习的转角位移方程来确定。因此，问题转化成如何求φ1。

3.2 位移法基本原理

位移法基本原理十分抽象，学生难以理解，讲解过程中穿插动画演示、课堂讨论、装置演示等环节，并与力法的基本概念相联系，强调力法与位移法的对偶性。

仍以超静定三杆刚架为例，重点阐述位移法基本系（见图7）形成的关键思想。构造的基本系应该是可以计算的，而且在基本系上可以把引起结构内力和变形的因素分开来考虑。讲解过程中一方面与力法基本系的构造思想联系起来，另一方面通过前述演示装置演示原结构和基本系的变形过程，并演示刚臂的“放松”和“锁住”效果，让看不见摸不着的“刚臂”变得形象化、可视化，加深学生的理解。然后，通过比较位移法基本系与原结构的差别，得出刚臂上的附加约束反力FR1=0 这个条件，并根据叠加原理，得出位移法基本方程，如下所示：

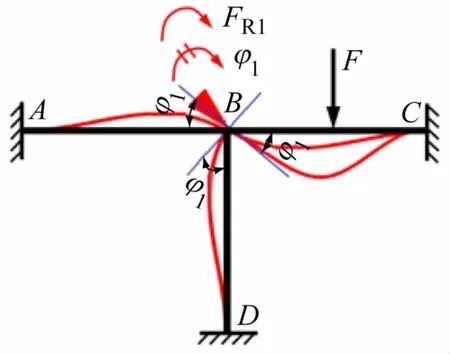
图7 位移法基本系

式中：k11为系数项，表示基本系仅受φ1=1 单独作用时附加约束1 处的约束反力；FR1F为自由项，表示基本系仅受外荷载作用时附加约束1 处的约束反力。此时，超静定结构求解的静力平衡条件和位移协调条件均已满足。

3.3 课堂讨论及课外研究设计

（1）请多个学生按照自己的构思操作演示装置，并讨论结构（原结构或基本系）在不同因素作用下的变形状态。

（2）讨论图2（a）中φ1、φ2和Δ3是否均应作为位移法基本未知量。通过课堂讨论，加深学生对独立的位移法基本未知量的理解。同时，要求学生列出此算例的位移法基本方程，求出位移法基本未知量并作弯矩图。

（3）成立课外研究兴趣小组，到实验室利用位移法基本原理的实验装置做实验，并记录实验数据，进行误差分析，提交实验报告。

4 结 语

位移法基本原理为结构力学课程的最重点和难点，通过自主开发的演示装置和实验装置，将理论教学与实验教学相联系，让看不见摸不着的抽象理论形象化、直观化，有效解决了“结构”力学学习中不见“结构”的问题。详细介绍了研制的演示装置和实验装置，演示装置和实验装置均可再现位移法超静定原结构和基本系的变形过程。加深了学生对2 种状态的理解：一是节点位移和荷载分别单独作用于基本系的状态，二是原结构中荷载引起内力和变形的状态。最后，阐述了理论与实验融合的位移法基本原理的具体教学方法。

通过研制的2 个实验装置将抽象的位移法基本系形象化、直观化，加深了学生对位移法基本原理的理解，强化了理论与实践的融合。