基于M估计强混合重尾序列结构变点的鲁棒检验
朱 玲,金 浩,乔宝明
(1.西安科技大学a理学院;b计算机科学与技术学院,西安 710054;2.重庆移通学院 公共大数据安全技术重庆市重点实验室,重庆 401420)
0 引言
自20 世纪20 年代以来,变点问题一直是国内外学者研究的热点,变点检测在经济、金融、工业等领域均有着重要的应用,尤其是对位置参数的统计推断研究引起了国内外学者的广泛关注。目前,对位置参数的统计推断研究主要从数据残差序列、变点数量、统计量、估计方法、抽样方法等方面展开。在残差序列方面,对于独立正态分布序列,Sen 和Srivastava(1975)[1]、Worsley(2012)[2]较早使用极大似然估计方法对相似的独立正态序列位置参数变点进行递归检验,但此类检验方法的功效不足。随后,Hawkins(2012)[3]分别利用贝叶斯和最大似然比两种方法研究了结构变点,得到了原假设下的渐近分布。
上述变点研究只考虑了时间序列独立或属于高斯分布的情况,然而,对于具有尖峰重尾特点的经济和金融数据,传统的研究方法可能不再适用。如高奎(2020)[4]结合金融数据的特点,对尖峰重尾序列的位置参数变点进行统计推断,发现当尾部分布显著偏离正态分布时,基于最小二乘估计的累积和检验的经验水平会出现严重扭曲。金浩等(2022)[5]研究了动态序列下的时变方差相依序列位置结构变点的比值型检验。针对具有尖峰重尾特点的序列,Robert等(2006)[6]提出了一种基于LAD的稳健KPSS检验,证明了在重尾情况下LAD 显著优于基于最小二乘估计的KPSS检验。随后,MacKinnon等(2021)[7]讨论了无限方差高阶自回归在M估计下的检验,并证明了在原假设下渐近分布是一个布朗桥,进一步拓展了M估计的研究。然而,累积和检验方法仍然需要对长期方差进行估计,而长期方差形式复杂,极大地增加了估计的难度。为了解决这个难题,Horvath 等(2008)[8]提出了比值型检验统计量,并探讨了采用其他比值型检验统计量进行研究的可行性。大量研究表明,比值型检验统计量对于需要估计长期方差的变点检验较为适用。
为获得更精确的临界值,针对序列的强混合性,常用的方法是通过重抽样方法逼近统计量的渐近分布。Bertail(1994)[9]研究了残差为独立同分布序列的重抽样性质。针对序列的特点,MacKinnon 等(2021)[7]介绍了Wild Bootstrap抽样方法,并根据不同核函数研究其逼近的有效性。Paparoditis 和Dimitris(2003)[10]指出,对于强混合序列,简单的重抽样方法存在较大的不足,而Block Bootstrap抽样方法可最大程度地保留原始序列的相依性,从而使得检验统计量不会因序列强相依性而出现经验势值偏低的现象。因此,本文从序列的强混合性特点、统计量及其鲁棒性检验三个方面考虑,选择Block Bootstrap抽样方法,基于M估计构建强混合重尾序列下的比值型检验统计量,以达到有效检测位置参数结构变点的目的。
1 假设与检验统计量构造
假定序列y1,y2,…,yn最多存在一个变点,其基本模型为:
其中,μ1、μ2是固定但未知的水平位置结构参数,s*是变点位置,εt是随机误差项,I{⋅}是示性函数,[·]表示向上取整。
若时间序列y1,y2,…,yn满足式(1),则考虑位置参数变点的检验问题。设原假设下不存在位置参数变点,即:
H0:μ1=μ2=μ
而备择假设下最多存在一个变点,变点时刻s*∊(0,1),即:
为保证检验的渐近有效性,对新息过程{εt} 和M估计函数ψM(∙)提出如下假设:
假设1:{εt} 是严平稳α-混合序列,对于某些有限的χ>0,χ'>0,存在常数C(χ,χ')>0 满足:
其中,α(h)(h=0,1,…)是α-混合系数。
假设2:{εt} 的分布F位于稳定吸收域中,其尾部指数κ∊(0,2],当κ>1 时,有E(εt)=0;当κ≤1 时,{εt} 是一个对称分布。
假设3:随机变量ψM(εt)满足如下假设:
(1)E(ψM(εt))=0;
(3)0<|E(ψ'M(εt))|<+∞,且对某些β>1有E|ψ'M(εt)|β<+∞;
M估计是稳健统计中最基本的方法,由Huber在1954年对极大似然估计加以推广而来。在考虑比值型检验统计量前,先给出参数M估计的定义。选定一个在R上的非负凸函数ρ,令:
其中,ρ是损失函数,有ρ'=ψM。为了方便统计量的构建,以ψM函数的形式重新表示式(3):
其中,θ̂为θ的M估计。
M 估计是一个大框架,包括经典的最小二乘估计、标准的Huber 函数、最小绝对偏差估计、截尾函数估计等。由于累积和统计量需要对长期方差进行估计,而该估计较为困难,因此,为了避免该缺陷,本文在Horvath 等(2008)[11]、Pestova 和Pesta(2018)[12]检验思想的启发下,提出基于M估计的比值型检验。统计量定义如下:
其中,μ̂(ψM)是对据数据y1,y2,…,yn进行M 估计得到的位置参数估计值;类似地,μ̂1(ψM)和μ̂2(ψM)分别是对y1,y2,…,y[ns]和y[ns]+1,y[ns]+2,…,yn进行M 估计得到的位置参数估计值。
2 检验统计量的相关性质及证明
2.1 检验统计量的渐近分布
为得到检验统计量在原假设下的渐近分布,先给出M估计相合性的引理。
引理1:如果假设1 至假设3 成立,那么在原假设H0下,有:
其中,B(⋅)表示一般的布朗运动。
证明:首先定义凸函数ρ,其表示为:
其中,u=n12(μ-μ̂(ψM))。对Zn(u)在u=0 附近进行一阶泰勒展开,有:

结合式(6)和式(7),本文重写式(5),得到:
利用导数的性质计算式(8)的最小值。令:
本文得到原假设下参数基于M估计的一致性,其可表示为:
引理1得证。(μ-μ̂1(ψM))和(μ-μ̂2(ψM))的证明过程与之类似,本文不再赘述。
定理1:假设yt由式(1)生成,若原假设H0和假设1至假设3成立,则当n→+∞时,有:
证明:假设μ=0,有:
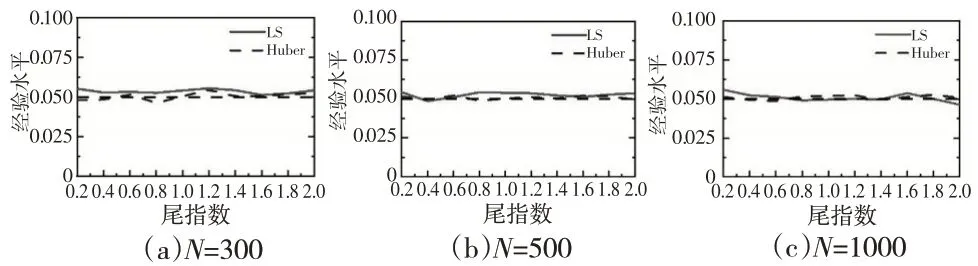
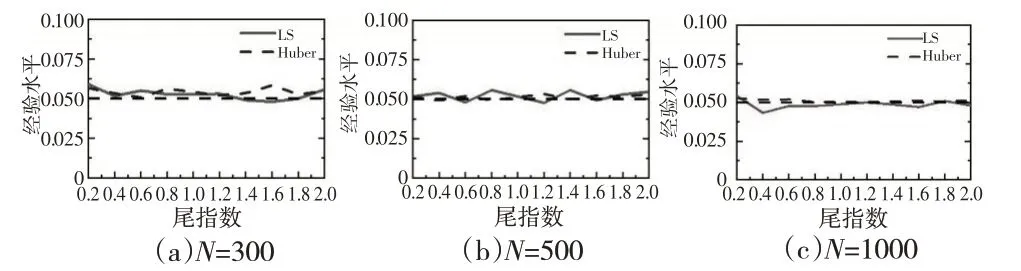
其中,B(s)(0 在满足假设1 至假设3 的条件下,结合Huskova 和Marusiakova(2012)[13]的研究中的引理4.3 和引理4.4,本文定义Ξn的分子为Λ1: 其中,ψM(ε̂t)=ψM(εt+μ-μ̂(ψM)) 。重新构造基于M估计的残差形式为: 利用微分中值定理、引理1关于参数u的全覆盖定理和ψ'M(εt)的中心极限定理,有: 因此,本文得到分子的渐近分布形式是一个布朗运动,即: 类似地,定义Ξn的分母为Λ2: 进一步区分分母的两个部分,分别用Λ21和Λ22表示: 与分子的证明类似,在满足中心极限定理的条件下,对应分母第一部分的渐近分布形式为: 同理,得到分母第二部分的渐近分布形式为: 结合式(10)至式(12),得到原假设下检验统计量的渐近分布,即当n→∞时,有: 定理1得证。 引理2:如果假设1 至假设3 成立,那么在原假设H1下,有: (1)当i=1,2 时,μ̂(ψM)-μi=Op(1); (2)当s*≠s时或者(1)成立; (3)当s*=s时,n12(μ̂1(ψM)-μ1) 和n12(μ̂1(ψM)-μ2)有与引理1相同的渐近分布。 证明:以引理2 中的第(1)条为例,与引理1 的证明思想类似,先定义备择假设下的凸函数ρ,零变点时刻为s*,则有: 利用反证法,先假设u=(μ-μ̂(ψM))=op(1)。为了证明的方便,定义Zn(u)=Z1n(u)+Z2n(u),具体可表示为: 固定Z2n(u) ,使得Z1n(u) 达到最小,且对Z1n(u)(式(14))在u=0 处进行一阶泰勒展开,有: 当满足u=(μ-μ̂(ψM))=op(1)时,Z1n(u)达到最小。而在备择假设下,参数估计的一致性还要求Z2n(u)同时达到最小。因此,利用相同的思想,对Z2n(u)(式(15))在u=0处进行泰勒展开,有: 并且满足: 此时,备择假设下参数估计的一致性与式(16)和式(17)矛盾,所以u=(μ-μ̂(ψM))=op(1) 只能使Z1n(u) 或者Z2n(u)其中一个达到最小,不能使Zn(u)的两个部分同时达到最小,与反证法中的原假设矛盾。因此,在备择假设下,参数估计是不一致的。同理,μ̂1(ψM)和μ̂2(ψM)各自的有偏估计证明与之类似,本文不再赘述,且最终对参数估计的分类如引理2中的第(2)条和第(3)条所示。引理2得证。 定理2:假设yt由式(1)生成,若备择假设H1和假设1至假设4成立,则有Ξn=Ξn(s*)。当n→∞时,有: 证明:受变点的影响,备择假设下检验统计量的发散性证明需要考虑三种情况:(1)s>s*;(2)s 当s>s*时,用μ1表示基于观察数据y1,y2,…,y[ns*]的位置参数,用μ2表示基于观察数据y[ns*]+1,y[ns*]+2,…,yn的位置参数。在备择假设下,结合引理2,具体考虑μ̂(ψM)-μ1=Op(1),μ̂(ψM)-μ2=op(1)的情况,其中,μ̂(ψM)是参数μ的M估计值。令Ξn的分子为Γ1: 式(18)中的第二项起决定性作用。 当s>s*时,变点在前半部分,分母的第一项受变点影响,而分母的第二项与原假设相同,且对应分母的第二项的发散速度为n12,只需将分母的第一部分重写为: 进一步考虑μ̂1(ψM)-μ1=Op(1) ,μ̂1(ψM)-μ2=Op(1) ,μ̂2(ψM)-μ2=op(1)的情况: 因此,结合式(19)和式(20)可知,分母的第一部分的发散速度为n。最后,结合式(18)至式(20)可得: 综上,统计量Ξn=Op(1) 。当s 定理2得证。 从理论角度分析,检验统计量在原假设下的渐近分布的显式形式是布朗运动的泛函,但其十分复杂,不能有效确定临界值。因此,选择一个科学的方法确定临界值意义重大。不失一般性,本文考虑重抽样方法中较为合适的Block Bootstrap抽样方法。后文将分别用经验水平和经验势体现原假设和备择假设下的检验功效。具体步骤如下: 步骤1:基于观测值y1,y2,…,yn计算M估计μ̂(ψM)。 步骤2:计算残差ε̂t=yt-μ̂(ψM),t=1,2,…,n。 步骤4:选择正整数m(m 定理3:如果定理1成立,且m→∞,m/n→0,那么当n→∞时,有: 证明:定理3的证明与定理1的证明类似,只需要补充证明Block Bootstrap 样本下参数估计的一致性即可。首先,有与式(9)相同的定义: 其次,需要证明Block Bootstrap 样本中残差部分和的收敛性。定义[hs]=[[Ls]/m],得到: 最后,当得到与引理1 相同的前提后,构造类似的凸函数ρ。同理,可得到与引理1相似的结论,有: 样本前半段和后半段子样本对应参数估计的一致性证明过程与之类似,本文不再赘述。 定理3证毕。 本文通过蒙特卡洛数值仿真来阐明基于Block Bootstrap抽样的比值型检验在结构变点研究中的有效性。大量文献认为m=Cn13是较为合适的,本文沿用该思想,定义C=5,在数值模拟中进行具体研究。设定基于M 估计的比值型检验统计量Ξn(s)包含的损失函数为ψM(x)=x,x∊R,表示经典的最小二乘估计(LS);ψM(x)=xΙ{|x|≤K}+Ksgn(x)Ι{|x|>K},x∊R ,表示标准的Huber 函数,K=1.345。进一步,设定数据yt的生成过程为: 其中,{εt} 是一个强混合序列。为了分析不同相依程度下检验统计量的检测效果,本文主要考虑两种情况:(1){εt}是一个AR(1)过程,εt=βεt-1+ηt,其中,{ηt} 是独立同分布的重尾序列;(2){εt} 是一个AR(1)-AR(1)过程,εt=βεt-1+ηt且ηt=θηt+ξt,其中,{ξt} 是独立同分布重尾序列。尾指数κ∊{0.2,0.4,0.6,0.8,1.2,1.4,1.6,1.8,2.0}。不失一般性,设定β=-0.6,θ=0.6,跳跃幅度∆∊{0.5,1,1.5},变点位置s*∊{0.3,0.5,0.7} ,显 著 性 水 平α=0.05 ,样 本 量N∊{300,500,1000},循环3000次。 图1表示在弱相依情况下最小二乘估计和Huber函数估计对应的经验水平,横轴表示尾指数,纵轴表示检验统计量在原假设下的经验水平,其中实线代表基于最小二乘估计(LS)的拒绝概率,虚线代表基于Huber函数估计(Huber)的拒绝概率。根据观察,图1展示的最小二乘估计和Huber 函数估计对应的经验水平都在5%的水平附近波动,在弱相依情况下,能够较好地支持原假设。 图1 比值型检验在H0 下的经验水平,εt ~AR(1) 图2表示在强相依情况下,最小二乘估计出现轻微扭曲,但该扭曲在可接受范围内,且随着尾指数和样本容量的增加,扭曲程度逐渐减小。而Huber函数估计的经验水平仍然在5%的水平附近波动,说明Huber 函数估计较最小二乘估计能更好地支持原假设。同样,随着样本量N的增大,经验水平波动程度减小。因此,在原假设下,基于Block Bootstrap 抽样的Huber 函数估计统计量能有效控制强混合重尾序列的经验水平。 图2 比值型检验在H0 下的经验水平,εt ~AR(1)-AR(1) 图3表示在弱相依情况下最小二乘估计和Huber函数估计对应的经验水平,横轴表示尾指数,纵轴表示检验统计量在备择假设下的经验水平,其中低灰度的实线、虚线、点线分别代表变点位置在0.3、0.5 和0.7 处基于最小二乘估计(LS)的拒绝概率,高灰度的代表基于Huber函数估计(Huber)的拒绝概率。基于M估计的比值型检验统计量在备择假设下的经验水平受样本量、跳跃幅度、变点时刻、尾指数等因素的影响。 图3 比值型检验在H1 下的经验势,εt ~AR(1),s*=0.3,0.5,0.7 不难发现,经验势具备以下特点:(1)经验势随着样本容量N的增加而增加,且逐渐趋于1。(2)跳跃幅度∆的增加使得经验势也相应增加。(3)当变点位置s*=0.5 时,LS的经验势略大于变点位置为s*=0.3,0.7 时对应的经验势。这说明,变点时刻越接近样本中心,LS 的经验势越大,也越易检测;而当变点位置在前端和后端时,经验势有所下降,虽两者相差不大,但检测效果均有一定的降低,该结果与已有结果相似。(4)Huber 函数估计下统计量的经验势随着变点时刻的靠后而变大,尤其当变点时刻s*=0.7时,经验势达到最大,这是因为变点时刻越靠后,统计量发散得越快。本文发现上述特征与定理2 的结论一致。(5)经验势随着尾指数增加而增加。 图4 表示在强相依情况下,最小二乘估计和Huber 函数估计对应的经验势。 图4 比值型检验在H1 下的经验势,εt ~AR(1)-AR(1), s*=0.3,0.5,0.7 图4中展现的规律与图3基本类似,但需要注意的是,在强相依情况下,LS 的经验势明显低于弱相依情况下的经验势,这是因为序列的强关联性导致统计量过于保守,无法有效拒绝原假设。并且,在强相依情况下,当跳跃幅度∆=0.5 时,统计量在Huber函数估计和最小二乘估计下的经验势均较小,但Huber 经验势略高;而当跳跃幅度∆=1,1.5 时,Huber 经验势随之显著增加,且在尾部较重的情况下拒绝概率仍比LS经验势高。说明当跳跃幅度较小时,经验势主要由跳跃幅度控制;但当跳跃幅度较大时,统计量对应的尾部异常值在Huber 函数估计下的经验势中起主导作用。而受强相依情况的影响,经验势随着尾指数增加的程度与弱相依情况下的程度不同。当κ≤0.8时,LS的经验势不超过0.1,这说明基于最小二乘估计的比值型检验对重尾序列的位置参数变点检测几乎是失效的;当κ>0.8 时,随着尾指数的增加,LS 的经验势随之增加;尤其是当κ>1.6 时,LS 的经验势增加幅度较为显著。当0.6<κ≤1.4 时,Huber的经验势明显高于LS的经验势;而当1.4<κ≤1.8 时,Huber的经验势和LS的经验势相差不大。 结合图3 和图4 不难发现,虽然在近高斯过程下,LS的经验势略高于Huber的经验势,但这种情况会随着样本量和跳跃幅度的增加而消失。即使在不同尾指数和相依程度下,估计方法也各有优势,但对于强混合重尾序列,尤其是在异常值较多的情况下,最小二乘估计不再适用,而以Huber函数估计为例的M估计将更有效。 本文通过一组财经数据对所提方法在实际应用中的可行性进行说明。采用2020年10月15日至2022年8月3日共370 个交易日的港币对人民币汇率数据进行实证分析,数据来源于https://www.chinamoney.com.cn/chinese/bkccpr/。港币对人民币汇率标准化后的数据为yt,如图5所示。 图5 港币对人民币汇率标准化后的数据(2020年10月15日至2022年8月3日) 从图5中可以发现,数据yt在水平方向存在明显的结构变化,将数据yt代入检验统计量,得到Ξn=1.0083。由数值模拟可知,利用Block Bootstrap 抽样方法确定的临界值Ξ0.05=0.8466。因此,在显著性水平α=0.05 的条件下,Ξn>Ξα,应当拒绝不存在变点的原假设。利用Pestova 和Pesta(2018)[11]的研究中的变点估计思想,选择Huber 函数估计对变点时刻进行估计,得到s*=0.8297。根据变点位置,汇率在2022年1月13日发生突变,整个样本序列被分为[1,306]和[307,370]两段,并计算得到前半段样本的水平位置参数估为-0.3588,后半段样本的水平位置参数为1.7154,其跳跃幅度大约为2。究其原因,2022年国家根据国内实体经济运行情况选择降准和降息,即中美货币政策脱钩,人民币承压贬值,因此相应港币对人民币汇率上升。 本文提出基于M 估计的比值型统计量来检验强混合重尾序列位置参数结构变点。首先,在基于最小二乘估计的累积和统计量对强混合重尾序列位置参数变点进行检验的基础上,将尾指数拓展到(0,2],并构造基于M 估计的比值型统计量,从而避免了长期方差估计的问题;其次,不同于传统最小二乘估计下统计量的渐近分布是列维分布泛函,基于M估计的比值型统计量在原假设下的渐近分布是布朗运动的泛函,并证明了备择假设下统计量的一致性;最后,考虑到序列的强混合性,利用Block Bootstrap 抽样方法来逼近极限分布以获得更为精确的临界值,从而实现对重尾序列位置参数变点的检验。数值模拟和实证分析结果表明,在重尾情况下,本文给出的基于M估计的检验方法是检测强混合序列位置参数变点的有效工具。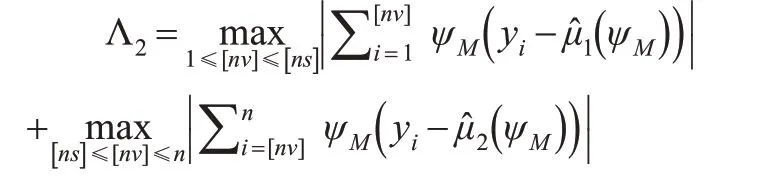



2.2 检验统计量的有限样本性质

3 数值模拟


4 实证分析

5 结束语

