中国全要素生产率增长率的效应识别及收敛性检验
钟世川,梁经伟
(1.广东金融学院 经济贸易学院,广州 510521;2.常州大学 吴敬琏经济学院,江苏 常州 213164)
0 引言
中国经济进入新常态以来,经济增速由高速增长转向中高速增长,经济增长目标也由追求经济速度转向高质量发展。然而,地区经济增长却呈现路径背离的双向分化态势:一些地区增速依然可观,而另一些地区增速却显著放缓或呈现相对衰退的边缘性倾向[1]。地区这种经济增长不平衡和分化态势愈加复杂,其背后的根源在于全要素生产率(TFP)增长率的“推力”与高速经济增长率的“拉力”不匹配。从2008 年国际金融危机开始,全球需求低迷就加剧了我国长期积累的经济结构和体制问题,导致TFP增长率持续下滑,进而使整体经济处于减速期,而欠发达地区增长率严重下行更成为我国整体经济的切肤之痛,尤其是一些地区的TFP出现了负增长,将降低我国经济中长期的增长水平。有关文献研究表明,伴随人口红利的消失,我国TFP 在“十四五”时期将会下降至1.7%[2]。伴随区域发展战略的演进,TFP 增长率全面放缓,区域分布形态由单极化向双峰演进,动态演化呈现低流动性和强持久性,落后地区赶超先进地区难度增大[3]。因此,新时代如何提高TFP增长率成为推动区域协调发展的关键。
不管是新古典增长理论,还是内生经济增长理论,均认为经济增长的核心在于提高TFP,并且将其视为区域经济发展不平衡的重要原因[4—6]。这些研究主要在中性技术进步假设下使用索洛余值法[7]、随机前沿法[8]、数据包络分析法[9]等对TFP 增长率进行测算和分解,忽视了技术进步非中性条件下TFP 增长率的核算及分解效应[10]。也有研究从TFP收敛性视角去揭示地区经济增长差距[11—14],但我国区域TFP收敛性的研究存在较大分歧。
综上,现有关于TFP增长率的测算方法及收敛性研究较为丰富,但中国实际TFP发展到底如何?整体TFP增长率是否存在阶段性特征?各区域TFP 增长率内部结构是否存在差异?各区域TFP 增长率变动是否存在收敛性?诸多问题值得深入研究。为此,本文的边际贡献有:第一,基于两类增强型技术进步生产函数构建TFP 增长率的测算方法,并深入剖析TFP 增长率的分解效应;第二,利用1978—2020年我国31个省份的GDP数据检验TFP增长率及分解效应的收敛性。
1 研究设计
1.1 TFP增长率的分解效应
本文用包含两类增强型技术进步的生产函数分析TFP增长率的分解效应,具体形式如下:
其中,θ∊(0,1)反映生产过程中资本投入与劳动投入之间的分配参数,ρ=(1-e)e是资本投入与劳动投入之间的替代参数,e∊(0,∞)是资本投入与劳动投入之间的替代弹性。
根据Hicks(1932)对技术进步方向∆t的定义,利用式(1)可得:
其中,任意变量x的变化率为x̂=ẋ/x。
根据式(2)可得:若∆=0 或e=1,则技术进步为中性。在e>1 时,若Â>B̂,有∆>0,则技术进步导致劳动边际增长率小于资本边际产出增长率,即技术进步偏向资本;若Â
将式(1)两边取对数,并在e=1 处进行二阶泰勒展开,经整理,有:
将式(3)两边分别对时间t求导,经整理,得到经济增长率的表达式为:
在规模报酬不变时,经济系统中经济增长率减去各生产要素对经济增长的贡献率便是TFP 增长率。根据式(4),有:
将式(2)代入式(5),经整理,得到TFP 增长率的分解效应:
由式(6)可知,TFP 增长率是资本增强型技术进步指数、劳动增长型技术进步指数、技术进步方向和及要素投入结构的复合函数,即TFP增长率可以分解为以下四种效应:
第一,资本增强型技术进步变化效应(T1=θÂt):由于0<θ<1,因此当资本增强型技术进步增长率Ât>0 时,TFP 增长率将上升,即T1 对TFP 增长率有促进作用。当Ât<0 时,结论相反。
第二,劳动增强型技术进步变化效应(T2=(1-θ)B̂t):由于0<θ<1,当劳动增强型技术进步增长率B̂t>0 时,T2对TFP增长率有促进作用。当B̂t<0 时,结论相反。
第三,技术进步偏向变化效应(T3=θ(1 -θ)ζt∆t):在ζt>0 情况下,当技术进步偏向劳动时,TFP增长率将下降,即T3 对TFP增长率有抑制作用;当技术进步偏向资本时,TFP 增长率将上升,即T3 对TFP 增长率有促进作用。在ζt<0 情况下,结论相反。

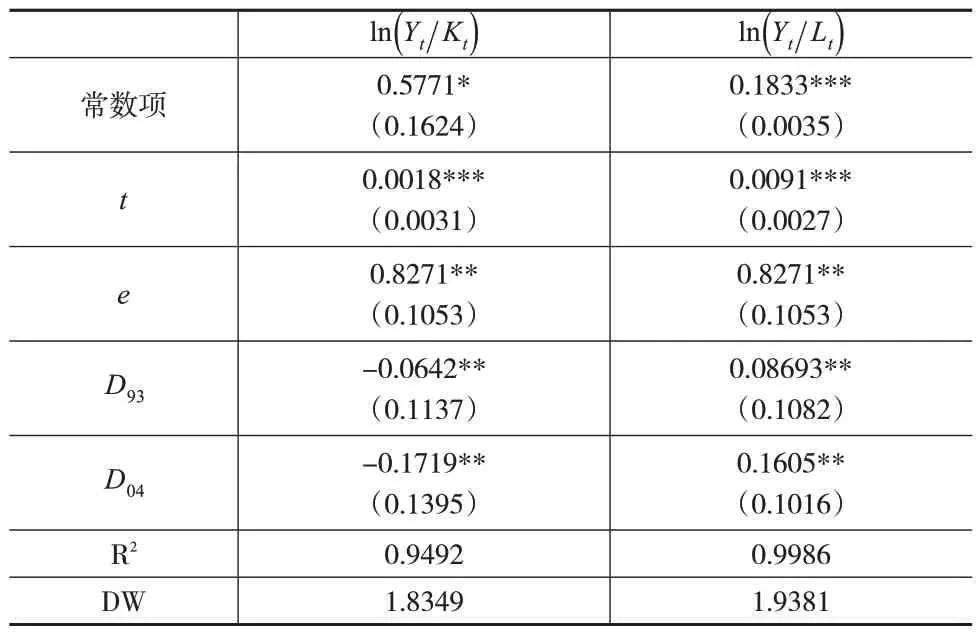
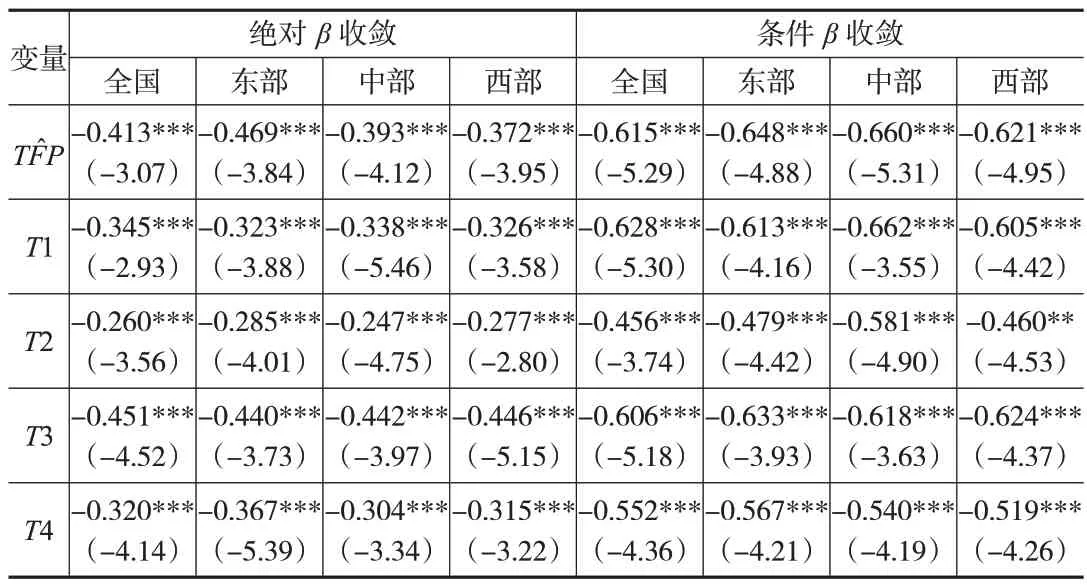
第四,要素投入结构变化效应ζt(K̂t-L̂t)):(1)当ζt>0 且e>1时,若K̂t>L̂t,则TFP增长率将上升,即T4 对TFP 增长率有促进作用;若K̂t 1.2.1 要素替代弹性的估计模型 要分析现实经济发展过程中TFP增长率变化及特征,就需先测算式(1)中的要素替代弹性。根据式(1),要素的边际产出等于相应的报酬,即MPK=rt和MPL=wt,整理得到如下表达式: 根据式(7)和式(8),可得要素增强型技术进步增长率的表达式为: 其中,e≠0。 鉴于式(7)与式(8)中的At和Bt不可观测,为得其估计值,本文假设At=A0eλKt+εKt和Bt=B0eλLt+εLt(λK和λL分别为资本和劳动增强型技术进步的平均增长率,εK和εL为随机冲击;假设初始年份A0=B0=1),将其分别代入式(7)和式(8)中,然后分别取对数,则有: 方程组式(10)中的随机冲击εK和εL可能存在同期相关性,此时需要用带约束的系统估计方法对方程组式(10)进行估计。为便于表述,将式(10)简写为: 鉴于本文采用1978—2020 年的数据进行实证检验,而在2004 年我国第一次进行全国经济普查后,国家统计局对1993—2004 年的GDP 序列数据进行了调整及修订,故设两个虚拟变量D93和D04来反映: 将上述虚拟变量纳入式(10)中,有: 1.2.2 TFP增长率的收敛性模型设定 (1)σ收敛。本文利用标准差来考察TFP增长率的σ收敛性。如果TFP增长率的标准差随时间缩小,则存在σ收敛;否则,不存在σ收敛。具体公式为: 其中,TF̂Pit为i地区t年的全要素生产率增长率。 (2)β收敛。一般包括绝对β收敛和条件β收敛,其对应的模型分别设定为式(14)和式(15): 其中,ϒit为i地区t年TFP 增长率或其分解效应;T为样本周期;X为控制变量,主要包括进出口贸易额占GDP 的比重、外商直接投资FDI 占GDP 的比重、经济发展水平(人均GDP)、研究与试验发展经费支出占GDP 的比重等;ε为随机扰动项。根据绝对β收敛和条件β收敛的系数可以计算出相应收敛速度v,即 本文选取1978—2020年中国31个省份(不含港澳台)的数据作为样本,其中将重庆的数据并入四川,所选取的指标数据均来自《新中国六十年统计资料汇编》和国家统计局官网。具体指标包括:(1)总产出Y,用各地区GDP来表示,鉴于每年公布的GDP为名义GDP,本文利用地区生产总值指数对其缩减,得到各地区不变价实际GDP(2000年=1000)。(2)劳动力投入L,用各地区全社会从业人员来表示。(3)资本投入K,利用雷钦礼(2013)[15]的研究中的永续盘存法计算各地区的资本存量来表示。(4)劳动报酬率w和资本报酬率r,首先,整理各地区收入法GDP核算中的固定资产折旧、生产税净额、劳动者报酬和营业盈余4项指标,并利用地区生产总值指数对这4项指标进行缩减得到其实际值(2000 年=1000);然后,假设生产税净额按资本和劳动比例分摊,则劳动所得=劳动者报酬+营业盈余×劳动者报酬/(固定资产折旧+生产税净额+劳动者报酬),资本所得=固定资产折旧+生产税净额+营业盈余×(固定资产折旧+生产税净额)/(固定资产折旧+生产税净额+劳动者报酬);最后,劳动报酬率=劳动所得/劳动力投入,资本报酬率=资本所得/资本投入。其中,全国及东、中、西部地区①东部地区包括北京、天津、河北、辽宁、上海、江苏、浙江、福建、山东、广东和海南;中部地区包括山西、吉林、黑龙江、安徽、河南、湖北和湖南;西部地区包括内蒙古、广西、重庆、四川、贵州、云南、西藏、陕西、甘肃、青海、宁夏和新疆。各指标数据均是各地区相应指标数据处理后的加总。 本文使用带约束的似不相关回归方法估计式(12),其结果如表1所示。在样本期内,中国资本投入与劳动投入之间的替代弹性值为0.8271,显著小于1,表明两种要素之间呈互补关系。 表1 方程组式(12)的估计结果 根据表1,可以计算出第二、三列的要素分配参数均值为θ=0.3482。利用式(2)和式(9),可以得到表2中全国技术进步偏向值:1979—2020 年,大多数年份全国技术进步偏向资本,∆t平均值为0.0203。以1993 年和2004年的数据调整为划分依据,将全国样本期划分为三个阶段(见下页表3):第一阶段是1979—1992年,第二阶段是1993—2003年,第三阶段是2004—2020年。在这三个阶段中,全国技术进步整体偏向资本,但第二阶段最为突出,∆t达到0.0262,是整个样本期均值的1.29 倍;第三阶段比整个样本期均值低0.14%。分区域来看(见表3),东、中、西部地区在这三个阶段中技术进步也均偏向资本;在第一阶段,东部地区技术进步偏向资本的程度是西部地区的9.19倍;在第二阶段,东、中、西部地区技术进步偏向资本的程度均明显提高,但东部地区是中西部地区的1.99 倍;在第三阶段,中部地区技术进步偏向资本的程度持续上升至0.0822,而东部地区却下降至0.0740。 表2 1979—2020年全国技术进步偏向值 表3 TFP增长率、要素投入变化与技术进步方向的阶段划分 根据下页图1,在样本期内,除2009年、2012年和2015年之外,全国TFP 增长率均为正,平均值为3.70%。分区域看,东中部地区TFP 的年均增长率超过全国平均水平,分别超出0.80%和0.27%;而西部地区TFP 的年均增长率比全国平均水平低1.98%。分阶段看(见表3),全国TFP增长率明显下降,第三阶段仅为第一阶段的53.32%。在三个阶段中,东、中、西部地区TFP 增长率也明显下降;与第一阶段相比,东、中、西部地区TFP增长率在第三阶段分别下降了0.0162、0.0439 和0.0712,由此可得,西部地区TFP 增长率下降最快,其下降速度是东部地区的4.39 倍、是中部地区的1.62倍。在第三阶段,东部地区TFP增长率仍高出全国平均水平,而中西部地区TFP增长率低于全国平均水平,且西部地区TFP增长率为负(-0.0108)。 图1 全国TFP增长率及分解效应 根据式(6),结合样本数据分析得到大部分年份ζt>0,易知全国技术进步方向与TFP 增长率方向大致一致,表明目前我国技术进步偏向资本有利于促进TFP增长率提高;而本文所得的要素替代弹性介于(0,1),故要素投入结构变化方向与TFP增长率方向相反,表明目前我国要素投入结构抑制了TFP 增长率。同时,从表3 可知,全国各阶段要素投入结构变化的值均大于技术进步偏向资本的值,两者差距从第一阶段的0.0461 增加到第三阶段的0.0690,暗示要素错配是我国TFP增长率持续下滑的主要原因之一。 根据图1,从全国层面看,2004 年资本增强型技术进步变化效应(-0.4175)和劳动增强型技术进步变化效应(0.2693)波动较为明显;受2008 年国际金融危机的冲击,2009年资本增强型技术进步变化效应(0.3823)、劳动增强型技术进步变化效应(-0.3197)以及技术进步偏向变化效应(-0.2734)波动较为明显。由表4 可知,在样本期内,资本增强型技术进步变化效应的均值为-0.0185,劳动增强型技术进步变化效应的均值为0.0261,技术进步偏向变化效应的均值为-0.0044,要素投入结构变化效应的均值为-0.0038。同时,结合图1和表4可知,在样本期内,技术进步偏向变化效应与TFP增长率的走势大致一致,但劳动增强型技术进步变化效应对TFP增长率影响最大。 表4 分区域TFP增长率的分解效应 根据表4,分区域看TFP 增长率的分解效应:1979—2020 年,东、中、西部地区资本增强型技术进步变化效应和要素投入结构变化效应均为负,其中,中部地区资本增强型技术进步变化效应最为突出(-0.0317),东部地区要素投入结构效应最为突出(-0.0273)。而东、中、西部地区劳动增强型技术进步变化效应和技术进步偏向变化效应均为正,其中,中部地区劳动增强型技术进步变化效应最为突出(0.0346),东部地区技术进步偏向变化效应最为突出(0.0249)。 根据表5,分阶段看TFP增长率的分解效应:在全国层面上,第三阶段资本增强型技术进步变化效应最为突出(-0.0389),第一阶段和第二阶段劳动增强型技术进步变化效应最为突出(分别为0.0257 和0.0421)。在分区域层面上,与第一阶段相比,第三阶段,东部地区资本增强型技术进步变化效应、劳动增强型技术进步变化效应和要素投入结构变化效应分别下降了0.0050、0.0214和0.0083,而技术进步偏向变化效应却增加了0.0234;第三阶段,中西部地区的资本增强型技术进步变化效应、劳动增强型技术进步变化效应和要素投入结构变化效应下降较为明显,但中部地区的技术进步偏向变化效应上升较为明显。 表5 分阶段TFP增长率的分解效应 根据式(13)考察全国及东、中、西部地区TFP 增长率的σ收敛性,结果如下页图2 所示。从总体上看,在样本期内全国及东、中、西部地区TFP 增长率的σ收敛并不显著,且存在一定的波动性。从局部上看,1999年前东、中、西部地区与全国TFP 增长率的标准差走势大致一致,但1999 年后西部地区与全国TFP 增长率的标准差走势较为接近。 图2 TFP增长率的σ收敛性检验结果 为了分析TFP增长率的β收敛性,本文采用固定效应模型对式(14)和式(15)进行估计,其结果如下页表6 所示。全国及东、中、西部地区TFP增长率、资本增强型技术进步变化效应、劳动增强型技术进步变化效应、技术进步偏向变化效应和要素投入结构变化效应均存在显著的绝对β收敛和条件β收敛,说明我国TFP增长率较低区域有向TFP增长率较高区域追赶的趋势,但最终稳态发展水平与不同区域的特定条件有关。从TFP 增长率的分解效应来看,全国及中西部地区技术进步偏向变化效应、东部地区TFP增长率呈现更为明显的绝对β收敛;全国及中部地区资本增强型技术进步变化效应、东部地区技术进步偏向变化效应呈现更为明显的条件β收敛。 表6 TFP增长率的β 收敛性检验结果 将表6中的估计系数转换成收敛速度作进一步分析:首先,从全国来看,TFP增长率、资本增强型技术进步变化效应、劳动增强型技术进步变化效应、技术进步偏向变化效应以及要素投入结构变化效应的绝对β收敛速度分别为1.27%、1.01%、7.17%、1.42%和9.18%,条件β收敛速度分别为2.27%、2.45%、1.45%、2.22%和1.91%。由此可以看出,全国要素投入结构变化效应的绝对β收敛速度最快,且资本增强型技术进步变化效应的条件β收敛速度最快。其次,从区域绝对β收敛速度来看,东部地区TFP增长率、劳动增强型技术进步变化效应和要素投入结构变化效应领先,西部地区技术进步偏向变化效应领先,中部地区资本增强型技术进步变化效应领先。最后,从区域条件β收敛速度来看,东部地区技术进步偏向变化效应和要素投入结构变化效应领先,中部地区TFP增长率、资本增强型技术进步变化效应和劳动增强型技术进步变化效应领先。 本文利用包含两类增强型技术进步的生产函数将全要素生产率增长率分解为资本增强型技术进步变化效应、要素投入结构变化效应、劳动增强型技术进步变化效应以及技术进步偏向变化效应。在此基础上,利用1978—2020 年中国省级数据进行实证检验,结果表明:第一,中国资本投入与劳动投入之间呈互补关系,样本期内技术进步大致偏向资本且在1993—2003 年最为突出。第二,全国TFP增长率明显下降,东中部地区TFP的年均增长率超过全国平均水平,而西部地区却低于全国平均水平。第三,在分解效应上,全国技术进步偏向变化效应与TFP 增长率的走势大致一致,但劳动增强型技术进步变化效应对TFP 增长率影响最大。第四,在收敛性上,全国及东、中、西部地区TFP增长率不存在σ收敛,但存在显著的绝对β收敛和条件β收敛。1.2 模型设定
1.3 数据说明及处理
2 实证分析
2.1 中国全要素生产率增长率的区域差异性分析

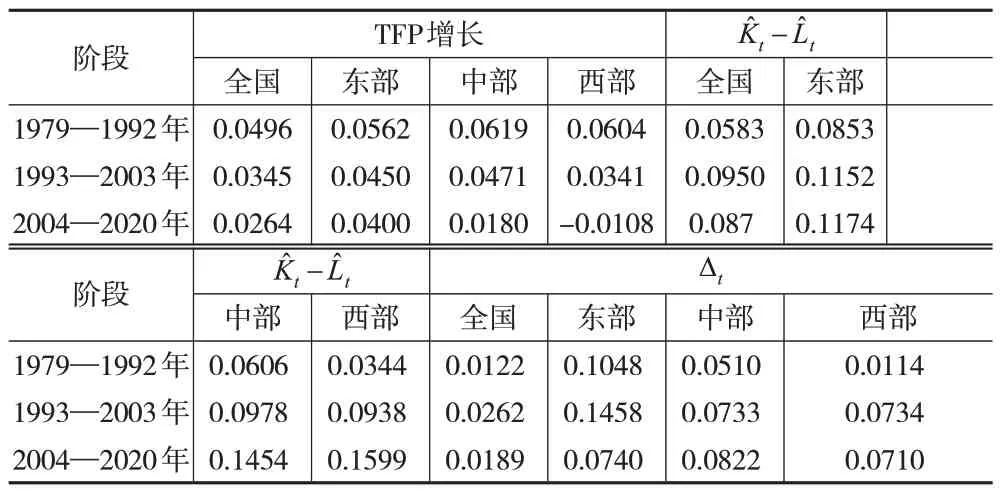
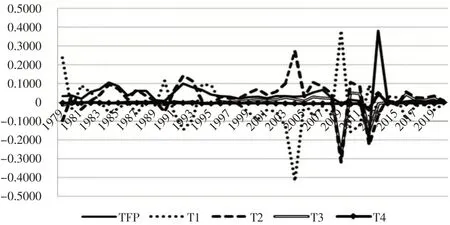
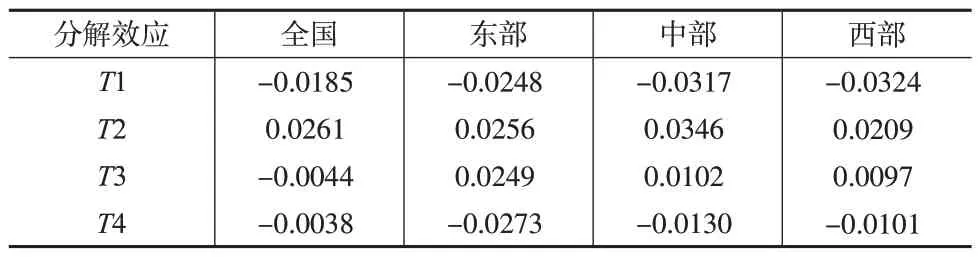

2.2 全要素生产率增长率的收敛性分析

3 结论

