一类折叠Gamma分布的尖峰厚尾性质及应用

陈明光，王源昌

（云南师范大学 数学学院，昆明 650500）

0 引言

尖峰厚尾性是许多数据具有的分布特点，如金融资产收益率、保险损失数据等。以参数方法拟合此类数据主要有两种方式：一种是单一分布拟合，即以单一分布来描述数据的分布特征[1—3]；另一种是构造分段函数，即针对数据的不同阶段分别采用相应分布拟合数据，最后综合构造最终分布。后者包括拼接分布法和组合分布法，两者都以多个分布拟合数据，但又有明显区别：拼接分布法不限分布个数，不关心各阶段分布间的连续性和可导性，最后所得分布往往是各阶段分布的碎片组合[4]；组合分布法一般采用两个分布，且在关注拟合效果的同时，通过设置阈值使最后构造的分布处处连续和可导。显然，组合分布法相比拼接分布法更有优势。如Luckstead 和Devadoss（2017）[5]构造双帕累托尾部对数正态分布拟合美国城市规模数据，效果良好。

Corry 和Ananda（2005）[6]首次提出组合分布思想并建立了固定权重的组合分布模型，其后，Preda 和Ciumara（2006）[7]、Corry（2009）[8]进行了扩展，又经Scollnik（2007）[9]、Nadarajah和Bakar（2014）[10]发展出权重可变且连续的组合分布模型，其在实际研究中已被广泛应用。王明高和孟生旺（2014,2017）[11,12]以不同分布组合构建三种组合分布并拟合了保险损失数据和巨灾损失数据；徐天群等（2009）[13]以Laplace 分布和Gumbel 分布构建组合分布来拟合深证成指收益率；王永茂和杨晓婷（2014）[14]构建了LogGED-GPD 组合分布来拟合全球洪水巨灾损失。

尽管组合分布的研究得到不断推进和扩展，但其阈值求解难度始终阻碍着某些组合分布的构造。那么，组合分布是否能以局部分布的峰值点为阈值点？又是否可采用单一分布构造组合分布？基于以上思考，考虑某些数据的尖峰厚尾特征，本文采用Gamma 分布构造组合分布。Gamma 分布的峰度系数是关于形状参数α的函数，本文希望组合分布能继承此特点，使之具有显著的尖峰厚尾特征。因此本文以α>1 时Gamma 分布的极值点作为阈值点，通过折叠、平移和伸缩变换构造完整的组合分布，如此可解决阈值点难求的问题。同时，扩展Gamma 分布的应用范围，使得新分布可应用于实数范围内的数据。

1 构造新分布——折叠Gamma分布

Gamma 分布是基于Gamma 函数的正向分布，含有形状参数α和尺度参数λ，可记为Ga(α,λ)。当参数α>1时，Gamma 分布的密度函数在处取极大值，即此处密度函数的导数值为零。本文基于Gamma分布的这一性质构造折叠Gamma分布。

1.1 折叠Gamma分布的构造

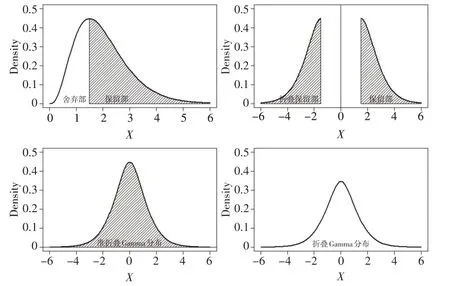
图1 折叠Gamma分布的构造过程

由图1可知，保留部与折叠保留部的函数解析式为：

准折叠Gamma 分布右半部和左半部的函数解析式为：

为了满足分布的正则性，令Gamma 分布舍弃部的积分为k，最终可得：

借助k对p1*(x)和p*2(x)进行同比例压缩，使其定义域内的积分均为1/2即可,即有：

定理1：若随机变量X服从折叠Gamma分布，则其密度函数具有如下形式：

证明：由式（2）易证折叠Gamma分布的密度函数为式（3）。

本文成功基于Gamma 分布构造了折叠Gamma 分布，折叠Gamma 分布不仅在实数域内任意点可导，满足非负性和正则性，而且适用于研究实数范围的数据。

1.2 折叠Gamma分布的基本性质

1.2.1 对称性

由图1可知，折叠Gamma分布显然关于x=0 对称，故其任意奇数阶矩为零，即：

其中，k为奇数。同时，分布的对称性表明其偏度系数始终为零。

1.2.2 尖峰厚尾性

本文将证明折叠Gamma分布的峰度系数是参数α的函数，且分布往往具有尖峰厚尾特征。

定理2：对于折叠Gamma分布，其方差存在，且为：

证明：结合分布的对称性和式（2）有：

即有：

定理3：折叠Gamma 分布的峰度系数存在，且为参数α的函数。

定理3 表明折叠Gamma 分布的峰度系数为参数α的函数。本文将以数值模拟的方式证明：参数α在较大范围内的分布具有尖峰厚尾性。具体过程为：在（1，80）这一范围内生成1000 个均匀分布随机数，然后将其从小到大排序并依次代入式（4）计算相应峰度系数值，结果如下页图2所示。

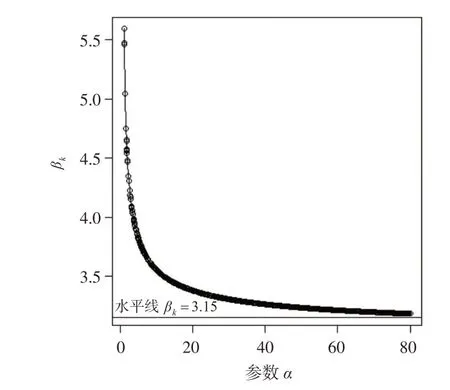
图2 折叠Gamma分布峰度变化

由图2 可知，随着参数α的增加，折叠Gamma 分布峰度系数的衰减速度越来越慢，直至趋于零；当α达到80时，峰度系数依然在3.15以上。由此可知，折叠Gamma分布的峰度系数在参数α的常用范围内大于正态分布的峰度系数，具有明显的尖峰厚尾性。

2 参数估计

2.1 矩估计

对折叠Gamma分布而言，需要估计参数α和λ，且分布的各奇数阶矩为零，因而需要采用其二阶矩和四阶矩构建方程。设样本二阶、四阶原点矩分别为A2、A4，由定理2和定理3可知，折叠Gamma分布的矩估计方程如下：

设θ=(α,λ)，在Newton-Raphson 算法下，θ矩估计的第t+1次迭代式为：

其中，J(θ)为Jacobi矩阵，S(θ)为梯度向量，且有：

2.2 极大似然估计

由于折叠Gamma 分布的密度函数含有Γ(α,α-1)项，导致其对参数α的导数过于复杂，因而在极大似然估计中仍采用Newton-Raphson 算法迭代出参数α和λ的近似估计结果。

设θ=(α,λ)，在Newton-Raphson 算法下，θ极大似然估计的第t+1次迭代式为：

其中，H(θ)为Hessian 矩阵，S(θ)为梯度向量。且有：

本文讨论了折叠Gamma分布在Newton-Raphson算法下的矩估计和极大似然估计，给出了相应估计的迭代式。

3 数值模拟

本文将以数值模拟证明有关折叠Gamma分布参数估计方法的有效性，表明可将其用于实际数据的研究。在Newton-Raphson 算法下以相邻两次迭代结果之差的绝对值小于105作为迭代结束条件。

3.1 随机数的生成

折叠Gamma 分布可在实数域内完整取值，故本文以第二类舍选法生成理论随机数。同时本文以α=4，λ=2为真值，在样本量为200、500、1000、2000、5000、10000、20000和50000时分别生成折叠Gamma分布随机数。

3.2 模拟参数估计

本文以相同随机数生成方法生成8组随机数，分别作为样本数据对折叠Gamma分布进行矩估计（MME）和极大似然估计（MLE），估计结果见下页表1。

表1 模拟数据在Newton-Raphson算法下的估计结果

由表1 可知，随着样本量的增加，整体而言矩估计下参数α和λ的绝对误差（AE）随样本量增大呈减小趋势。在极大似然估计中，参数α估计的绝对误差随样本量增加的变化趋势不稳定，但整体依然较小；参数λ估计的绝对误差总体呈减小趋势且都在0.1以下。总体而言，在Newton-Raphson算法下，矩估计和极大似然估计中参数α和λ的估计结果随着样本量增加逐渐趋于真值，表明估计结果较为可靠。

3.3 模拟参数估计平均结果

除了单组估计外，本文还用多组随机数进行参数估计，以估计的平均结果考察两种方法的可靠性。因而，本文在各样本量下用50 组随机数进行参数估计，并计算参数的估计结果、绝对误差和均方误差（MSE），结果见表2。

表2 模拟数据在Newton-Raphson算法下的平均估计结果（50组）

由表2 可知，与单组估计相似，矩估计和极大似然估计中参数α和λ的绝对误差总体依然随样本量增大呈减小趋势。总体而言，参数α估计的均方误差随样本量增大而减小，且α的均方误差在极大似然估计下更小；参数λ估计的均方误差随样本量增大而减小，且在极大似然估计下更小。因而，随着样本量增大，参数估计的均方误差趋于减小，同时，极大似然估计下的均方误差总体小于矩估计，即极大似然估计结果相对更为可靠。

4 基于现实金融资产收益率的实证对比分析

本文以沪深300指数收益率为例，将折叠Gamma分布用于实际金融收益率数据的拟合，并与正态分布对比，检验其效果是否确实优于正态分布。本文对折叠Gamma分布进行矩估计和极大似然估计，由于在正态分布下两种估计的参数估计结果相同，因而未对其加以区分，统一用Normal 表示。同时，算法迭代结束条件与数值模拟时相同。

选取2017 年12 月14 日 至2022 年6 月28 日沪 深300指数收益率数据作为实证研究数据，为了剔除新冠肺炎疫情这一突发事件的影响，本文剔除了2020 年1 月3 日至6月4日的100个交易日数据，整体共有1000个交易日的收益率数据。整体数据分布如图3所示。

图3 沪深300指数收益率频率分布直方图

由图3可知，沪深300指数收益率主要集中在（-3，3），对称性较强。经计算，其峰度系数为5.09，大于正态分布的峰度系数，且Anscombe-Glynn 峰度检验的P 值远小于0.01，即峰度系数显著大于3，数据具有显著的尖峰厚尾性。故以此数据检验折叠Gamma分布对尖峰厚尾数据的拟合效果是合适的。

4.1 参数估计与数据拟合

以所选数据为样本，折叠Gamma 分布和正态分布的参数估计结果及相应AIC和BIC的计算结果见表3。

表3 沪深300指数收益率参数估计结果

由表3可知，对于折叠Gamma分布，在矩估计下，参数α和λ的估计值都介于1 到2 之间。在极大似然估计下，参数α只有在样本量为800 时为8.669，其余各组均接近6；参数λ只有在样本量为500时为4.492，其余各组均在2到3之间。在正态分布的估计中，参数μ都处于0附近，参数σ2则在1.5左右，具有比标准正态分布更“矮胖”的分布形态。

同时，表3 呈现了各拟合分布下的AIC 和BIC 值。对于折叠Gamma 分布和正态分布，两种估计下折叠Gamma分布的AIC和BIC值整体小于正态分布，因而可认为折叠Gamma分布的数据拟合效果优于正态分布。对于折叠正态分布的两种估计方法，除了n=200 以外，其余各组数据矩估计的AIC和BIC值都明显小于极大似然估计，因而随着样本量增大，矩估计下的分布更适合拟合数据。

为了更加直观地认识折叠Gamma 分布对沪深300 指数收益率的拟合情况，本文绘制了两种分布对数据的拟合图，如图4所示。

图4 沪深300指数拟合效果

图4 呈现了两种分布对各组样本数据的拟合效果。对于折叠Gamma分布，随着样本量增大，矩估计下的分布与数据的吻合程度逐渐提高，对数据的拟合效果变好；而极大似然估计的拟合效果在各组数据中差异不大。同时，在各拟合图中，矩估计的拟合分布相对于极大似然估计具有更明显的尖峰特性，极大似然估计的拟合分布相对平滑。相对于正态分布而言，矩估计和极大似然估计下的折叠Gamma 分布明显都更具有拟合优势，拟合分布与数据的契合度更高。这与AIC和BIC判别结果一致。

4.2 沪深300指数收益率预测

本文基于沪深300 指数收益率各数据样本量下的已有估计分布对2022 年6 月29 日至8 月31 日的沪深300 指数收益率进行预测。先以第二类舍选法在已有估计分布下生成与预测部分数量相同的随机数作为预测收益率，比较相应时段的实际收益率与随机数的分布差异，以此衡量各估计分布的预测效果。实际收益率与预测随机数分布情况如图5所示。

图5 沪深300指数实际收益率与预测随机数盒型图

图5 呈现了实际收益率与递增数据样本量下各分布下预测随机数的分布情况。在各样本量下，正态分布预测随机数与实际收益率的分布差异最大，折叠Gamma 分布矩估计和极大似然估计预测随机数的分布与实际收益率相对更接近，但两者对比则随样本量递增表现不一。这表明两种估计下折叠Gamma分布的预测效果虽然会随样本量递增而变化，但总体上优于正态分布，即折叠Gamma分布的预测效果相对更好。

为了量化各组预测随机数与实际收益率的分布差异，本文以各组随机数与收益率分布的JS 距离作为判别依据，计算结果如表4所示。

表4 沪深300指数预测随机数与实际收益率的JS距离

由表4 可知，在各数据样本量下，正态预测随机数与实际收益率的JS 距离最大，折叠Gamma 分布两种估计下预测随机数与实际收益率的JS 距离相对更小，且全局而言依然小于正态预测随机数与实际收益率的JS距离的最小值。这进一步表明折叠Gamma分布的预测效果优于正态分布。

5 结论

本文从考虑分布的尖峰厚尾特征出发，鉴于Gamma分布的峰度系数可由参数α控制，以Gamma 分布为基础构造一种新分布，使其在继承Gamma 分布峰度系数特征的同时弥补Gamma分布只能应用于正向数据的缺陷。基于以上考虑，本文由Gamma 分布成功构造了满足以上特征的新分布，将其命名为折叠Gamma 分布。折叠Gamma分布的构造在采用组合分布构造思想的同时还避免了阈值求解难题。在成功构造分布的基础上，本文简单讨论了分布的性质，并在Newton-Raphson 算法下给出了分布的矩估计和极大似然估计，接着以数值模拟实验证明了估计的可行性，最后以沪深300指数收益率数据进行实证对比分析，表明折叠Gamma 分布相比于正态分布更适合拟合具有尖峰厚尾特征的数据。

本文构造了一种新的、具有尖峰厚尾特征的对称分布，为研究具有此种特征的数据，特别是金融数据的分布特征提供了一个新的分布选择。另外，本文构造的折叠Gamma分布在继承Gamma分布特征的同时扩展了Gamma分布的应用范围，将Gamma 分布的左偏特性扩展到折叠Gamma分布的对称性，使之能移植到实数范围的数据。

由于折叠Gamma分布的密度函数含有关于参数α的上不完全Gamma 函数，因而本文未能得到分布参数的确切估计量，也未能挖掘分布及其估计量更多的统计性质。因此，在进一步的研究中，探寻并描述折叠Gamma分布更多优良的统计性质是一个重要的研究方向。