基于新权重函数的MIX-GARCH-L模型及其应用

2024-05-15 06:48杨炜明

统计与决策 2024年8期

杨炜明，刘涛，王琴

（1.重庆工商大学a.数学与统计学院；b.长江上游经济研究中心，重庆 400067；2.重庆对外经贸学院大数据与智能工程学院，重庆 401520）

0 引言

在各种金融数据分析中，基于高频数据信息和历史信息来预测未来波动率已成为一个重要的研究方向，在金融市场分析中，波动率分析的主要目的在于预测金融市场的波动性。已有对于波动率的研究主要有两类：一类是利用最新的低频数据变量，并采用参数模型来测量和预测波动率[1,2]；另一类是利用非参数或者半参数估计方法，通过分析高频交易数据对波动率进行度量和预测[3—5]。以上方法虽都能较好地度量波动率的某些结构特征，但也存在各自的不足之处，主要原因在于上述模型都是基于同一数据频率来进行相关分析，限制了高频变量的选取，并且低频的参数估计方法没有充分利用高频数据中的有效信息，从而影响波动率预测的精确性。

已有研究更侧重于从低频经济数据中提炼信息，而不太考虑日间或日内高频交易数据的应用[1—9]。然而，日内高频交易数据蕴含了丰富的有效信息，对于短期波动率预测具有重要价值。此外，这类模型在权重分配上通常只考虑数据的时间顺序，也就是假设过往时期的低频变量以相同的方式影响波动率。这种假设在考虑外生低频数据变量的长期效应时可能适用，但并不适用于从日内高频交易数据中提炼信息。不适用的主要原因是：在不同交易日的高频交易过程中，数据的权重可能会随着市场条件和交易策略的变化而变化。为了更好地利用日内高频交易数据，本文引入更有效的权重函数，以便准确反映高频交易数据在波动率预测中的实际价值，从而更有效地从日内高频交易数据中提取有价值的信息，为短期波动率的预测提供更准确的依据。

1 模型构建

1.1 新权重函数构建

本文构建一种新权重函数，使各高频交易数据所获得的权重差异不仅取决于其取值大小，而且受到与其相邻数据差异的影响。具体来说，当某一数据的取值越大时，其与其他数据之间的差异也会越大，进而导致各高频交易数据之间的权重差异扩大。这意味着高频交易数据对未来波动率的冲击效果将更加显著。这种设定有助于更加准确地预测市场波动，尤其是短期内的波动情况。通过对各高频交易数据赋予恰当的权重，可以更好地揭示其内在的联系和影响，为投资者和交易者提供更有价值的参考信息。考虑到某些高频交易序列中会包含高频数据的实时波动、交易特征及其冲击效果，本文在参考王江涛等（2021）[10]提出的权重函数的础上进行改进，提出采用以下形式的权重函数来提炼高频数据：

其中，xi,j/m为某种高频时间序列在每个时间节点上的取值，比如高频资产收益率、高频股票交易量等。因为在实际情况中xi,j/m会出现小于0的情况，所以在分析时对xi,j/m取绝对值，从而保证权重的非负性。

新构建的权重函数w(j,λ)具有以下特征：（1）新权重函数在形式上与传统权重函数有一定相似之处，但新权重函数的参数以及分布形式都由样本数据决定；（2）只要选取合适的高频交易时间序列xi,j/m作为自变量，就可以使高频数据被赋予的权重与其未来波动率产生的冲击效果相符；（3）如果xi,j/m是除高频收益率之外其他的高频时间序列，那么在用新构建的权重函数w(j,λ)提炼高频数据信息时，就能同时利用多种高频时间序列，从而使数据中的有效信息得到充分利用。

1.2 构建MIX-GARCH-L模型

为充分提炼高频交易数据中的有效信息来预测未来波动率，仿照普通MIDAS方法和GARCH-MIDAS模型，在传统GARCH模型的基础上引入新权重函数来构建模型：

其中：μt表示日间收益率，σt为日间收益率的条件标准差，μi,j/m为日内高频收益时间序列；xi,j/m为高频交易过程中伴随高频收益时间序列μi,j/m产生的某种高频时间序列；独立同分布的误差项εt满足E(εt)=0,D(εt)=1；ϑ、α、β为模型的未知参数，和一般GARCH、GARCH-MIDAS模型一样，设定模型参数为非负常数；p、q为模型的滞后阶数，在实际中可以通过样本数据和AIC、BIC等信息准测来确定。新波动率模型通过构建的新权重函数w(j,λ)将两种高频数据xi,j/m、μi,j/m与低频数据μt相结合，从而利用多种混频数据信息来度量和预测未来波动率。

虽然以往研究也考虑将日内高频收益率应用于波动率模型，但往往以等权重的方式融合高频收益率，未能充分利用高频数据信息。本文提出的MIX-GARCH-L 模型在以往只能使用一种高频数据的基础上，引入其他高频数据，可进一步提取高频数据中的有效信息。而在高频交易过程中，会产生多种高频数据信息，如高频收益率、高频成交量以及其他高频时间序列等，这些都属于选择项。将新构建的权重函数w(j,λ)用于提炼高频收益率中有用的信息；为了避免伴随序列xi,j/m和日内高频时间序列μi,j/m中的信息重合，并考虑波动率相关指标以及日常交易中投资者决策行为等影响因素，本文选取高频成交量序列作为伴随序列xi,j/m。

2 参数估计

由于MIX-GARCH-L模型拥有全新的模型形式，因此需要重新研究新模型中的参数估计问题。本文参照普通GARCH 模型中的参数估计流程，对MIX-GARCH-L 模型采用拟极大似然估计法来实现对模型参数的准确估计，设定MIX-GARCH-L模型的对数似然密度函数为：

则MIX-GARCH模型的拟极大似然函数为：

其中，σt2为模型的条件方差，θ=(u,α1,α2,…,αp,β1,β2,…,βq,λ)为参数向量，令θ0为θ的真实参数L(θ),U代表整个参数向量空间。MIX-GARCH-L 模型的拟极大似然函数从形式上看和普通的GARCH模型的似然函数类似，但由于σt2内具有复杂的参数结构，因此使得MIX-GARCH-L模型的参数估计理论分析变得十分困难。

带有未知参数，在这种情况下使得矩阵Α0、Β0的形式会更加复杂，无法给出具体的渐近协方差形式，对定理结果的使用将会造成一定阻碍，故本文计划借鉴Buhlmann（1997）[11]提出的Service-Bootstrap 方法来计算渐近协方差。在数据生成机制保持不变的条件下，Service-Bootstrap方法能够利用误差项的独立同分布特性，通过迭代来获得协方差矩阵的准确估计。

3 数值模拟

为了验证参数估计的实际效果，本文构建模拟数据并采用Service-Bootstrap 方法进行检验，采用两组不同的模拟数据来进行实证检验。第一组模拟数据的产生机制如下：

第二组模拟数据的产生机制为：

3.1 参数估计结果分析

数值模拟中分别设定n=300，n=500，n=1000，以及n=2000，采用梯度下降法，应用R语言编程设计实现参数的估计，其中，BIAS代表数值模拟的估计量与真实值之间的偏差，SE为用Service-Bootstrap方法算出的模型参数估计量的标准误差，SD表示估计量标准离差，CP 表示在95%的置信水平下数值模拟的覆盖率，参数估计结果如表1所示。

表1 当误差项服从正态分布时参数的估计结果

下页表2给出了当误差项η2t服从t(10)时数值模拟的参数估计结果，首行表示收益率条件方差模型的参数真实值，其他行表示在不同试验次数n下各指标的取值。从表2数值模拟的结果可知：ω、α、β在不同实验次数n下的最大偏差绝对值分别为0.095%、0.093%、0.183%，最小偏差绝对值分别为0.011%、0.018%、0.022%。故可证明本文使用的Service-Bootstrap方法依旧能准确有效地估计出模型真实参数，即使在样本量n=300 的情况下依然有效。数值模拟中的SD值和SE值同样也都比较接近，因此可以证明上文中渐近协方差的表达式以及估计协方差的Service-Bootstrap 方法都是准确有效的，并且CP 结果显示数值模拟在95%的置信水平下覆盖率基本上都在95%以上，说明参数估计的理论分析结果合理。

表2 当误差项服从t分布时参数的估计结果

3.2 对照组分析

为进一步比较新权重函数和其他权重函数在检验参数估计效果上的区别，本文在上述两组不同模拟数据的基础上，赋予模拟数据新权重函数w(j,λ)、指数Almon 权重函数以及Beta权重函数来进行参数估计，对比在误差项满足不同分布及使用不同权重函数的情况下的参数估计效果。本次实验中参数估计方法使用Service-Bootstrap 方法，试验次数n设置为100。

在表3 的第一组模拟数据中，误差项ε1t服从均值为0、方差为0.02的正态分布，在赋予三种不同权重函数的情况下，发现本文提出的新权重函数w(j,λ)在估计模拟数据的参数时，其SE 和SD 值均小于指数Almon 函数和Beta函数，预测效果为三种权重函数中最优的。在指数Almon权重和Beta 权重的比较中发现，当估计相同参数时，指数Almon权重函数的误差值比Beta权重的误差值更小，说明指数Almon 权重函数相比于Beta 权重函数而言更适合误差项服从正态分布的参数估计情况。

表3 当误差项服从正态分布时，不同权重函数下的参数估计结果

在表4 的第二组模拟数据中，当其误差项η2t服从t(10)时，数值模拟在三种不同权重函数下的参数估计结果显示，本文提出的新权重函数w(j,λ)在估计模拟数据的参数时，其SE 值和SD 值都小于指数Almon 函数和Beta 函数，预测效果同样为三种权重函数中最优的。在新权重函数和指数Almon 权重函数下，截距项α的SE 值均为最小的，参数ω的SE 值居中，参数β的SE 值最大。而在Beta 权重函数中，参数ω的SE 值最小，参数α的SE居中，参数β的SE 值最大。通过对比发现，新权重函数相较于其余两种权重函数，其参考估计结果均较优、误差更小。

表4 当误差项服从t分布时，不同权重函数下的参数估计结果

4 实例应用

本文选取上证综合指数2018年1月2日到2022年1月2日共计974个交易日的数据，因使用上证综合指数每日的涨幅来代替日收益率会导致误差过大，故仿照高频数据的处理方法，以每天收盘指数的对数值减去上一天收盘指数的对数值作为当天的日收益率，结果如图1所示。

4.1 基准模型

本文运用标准GARCH 模型、GARCH-RV 模型、GARCH-M 模型，以及所提出的MIX-GARCH-L 模型，对上证综合指数的实际交易数据进行分析。通过对比不同模型在波动率分析和预测方面的实际表现，以验证MIX-GARCH-L模型的预测精度。

其中，标准GARCH模型以GARCH(1,1)模型作为基准模型，GARCH(1,1)模型的表达式为其中，α1,β1≥0,α1+β1<1。在GARCH-RV 模型中，以作为已实现波动率RV，即采用相等权重来提炼第t个交易日中高频收益率数据中的有效信息；GARCH-M模型基于MIDAS方法给高频数据分配不同的权重，以此来提炼高频数据的有效信息，从而进行上证指数波动率分析。之所以引入GARCH-RV模型，是为了与GARCH-M模型和本文提出的MIX-GARCH-L模型进行比较，GARCH-M模型与MIX-GARCH-L 模型提取高频数据中的有效信息的方式类似，用其余的模型进行比较无法说明MIX-GARCH-L模型的信息提炼度更好，预测效果更优。

4.2 检验结果分析

本文选用上证综合指数2018 年1 月2 日至2022 年1月2日的高频交易样本，共计974个交易日，每个交易日每隔60分钟进行一次数据采样。采用常规的高频数据处理方法，通过计算每天的对数收盘价与前一天对数收盘价的差值，得出当天的日收益率。为得到上证综合指数收益率的预测结果，本文先选取前874个交易日的高频数据来估计模型的参数，并据此来预测最后100 个交易日的波动率。各模型基于前874个交易日数据的参数估计结果为：

标准GARCH模型：

GARCH-RV模型：

GARCH-M模型：

MIX-GARCH-L模型：

在上述参数估计结果中，所有模型的滞后阶数都是利用参数估计的显著性以及似然比统计量来确定的，模型公式下对应括号内的数值为参数估计量的标准误差。对比上述三种模型的参数估计结果可发现，标准GARCH 模型、GARCH-RV模型、GARCH-M模型以及MIX-GARCH-L模型的参数估计结果均在5%的水平上显著。在上述四种模型中，GARCH-M模型的系数标准误差最小，MIX-GARCH-L模型其次，标准GARCH 模型的标准误差相对最大，GARCH-RV 模型与标准GARCH 模型在系数α1上的标准误差比较接近，但GARCH-RV模型β1系数的标准误差相较于标准GARCH 模型更小。而GARCH-M 模型和MIX-GARCH-L模型的参数标准误差差距较小，GARCH-M模型的系数标准误差相对更小。

将上述模型的波动率预测值与真实值进行对比分析，以验证模型的预测表现。本文以标准GARCH模型作为波动率的真实水平，则其余模型的波动率表现如表5所示。

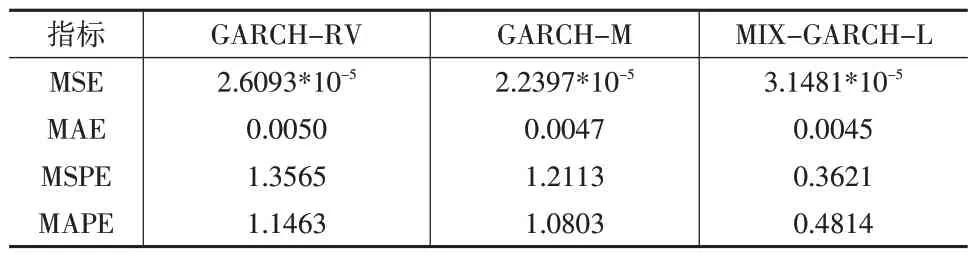
表5 三种模型预测波动率结果

5 结论

本文在波动率模型的基础上，根据高频数据交易特征引入一种新权重函数，并构建了一种新模型——MIX-GARCH-L 模型。该模型能有效提炼高频交易数据中的有效信息，准确、稳健地预测出波动率。基于数值模拟以及实例应用得出以下结论：第一，本文提出的新权重函数能够更高效地提炼数据中的有效信息，并与相关低频数据变量结合，相比仅利用同频数据信息，能更准确、更稳健地度量和预测波动率。因此，在研究与波动率相关的其他问题时，如风险防控、资产风险评估等，可考虑应用这种新权重函数。第二，传统的权重赋予方法在度量和预测波动率时，并不能有效提炼出高频数据中的信息。相比之下，根据交易特征（如高频交易量或其他伴生的高频交易信息）来分配权重的新权重函数，能更有效地提炼出高频数据中的有效信息。在此基础上构建的MIX-GARCH-L 模型也能更准确地预测波动率。第三，新权重函数的引入使得MIX-GARCH-L模型具有了新的模型形式和参数结构，但拟极大似然估计方法仍能准确估计出新模型的参数，并且参数估计量也满足一致性、渐近正态性等定理，从而保证了模型的可靠性和稳定性。

本文提出的新权重函数为高频交易数据提供了一种全新的数据提炼方法，进一步丰富了分析混频交易数据的手段。同时，基于这种新权重函数构建的MIX-GARCH-L模型也为研究波动率提供了更多的可能性。参照本文的方法，在处理涉及高频数据的问题时，如果同时拥有低频和高频数据，那么可以优先考虑使用新权重函数来提炼高频数据中的有效信息，解决数据频率不匹配的问题。除了在波动率模型中的应用，新权重函数在混频数据回归等模型中也有广泛的应用前景。