广义导数及其在极值问题中的应用
阮诗佺, 于小珊, 于 野
(1.厦门大学 数学科学学院,福建 厦门 361005; 2.厦门大学 管理学院,福建 厦门 361005)
0 引 言
通过等价关系进行等价分类,将复杂的问题转化为简单问题,是十分重要的数学方法.例如,同一数域上同型矩阵之间的相抵关系、同阶方阵之间的相似关系与合同关系等,都是矩阵之间的等价关系.这些矩阵的等价关系和标准形理论贯穿了整个高等代数的始终[1-2].
微积分中的同阶无穷小和等价无穷小在极限理论和计算中有着重要的作用[3-5].本文将等价思想应用到无穷小理论当中,证明同阶无穷小与等价无穷小是函数之间的两种等价关系,并将它们应用于解决具体的函数极值问题.
导数是微积分的核心内容之一,是研究函数理论的重要工具,比如微分中值定理的应用[6-7],求函数的单调性与极值问题等等[8-9].不仅如此,它还广泛应用于其它各个学科之中,比如高等代数的多项式理论中关于重因式的判定等.通过与等价无穷小相结合,可以更好地发挥导数的作用.众所周知,洛必达法则是求函数极限的最重要工具之一,而通过与等价无穷小相结合,利用简单的函数替代复杂的函数,可以大大简化其求极限的过程.例如下面的例子(其中首尾两个等号利用等价无穷小,中间两个等号利用洛必达法则):
虽然导数理论已经相当完善,但是对于求具体函数的导数,一般来说是比较困难的,比如求多重复合函数的高阶导数等.因此,应用导数方法求函数的极值问题,微积分教材中只介绍了第一充分性定理与第二充分性定理,它们只涉及低阶导数(一阶与二阶).并且,上述两个充分性定理的应用具有较大的局限性.比如,第一充分性定理需要判定函数在某一个点局部导数值的符号,而第二充分性定理仅适用于一阶导数为0,但是二阶导数非0的情形.对于更一般的情形,如何判断函数的极值是一个自然而然产生的问题.
具体说来,如果f′(x0)=0,但是无法确定f(x)在x0点局部的导数值的符号,那么无法使用第一充分性定理来判断x0是否为f(x)的极值点;如果f′(x0)=f″(x0)=0,那么无法根据第二充分性定理来判断x0是否为f(x)的极值点.当第一充分性定理与第二充分性定理的条件都不满足的情况下,如何解决函数极值问题?一般考虑用泰勒公式来处理.有下列结论:设函数f(x)在x0处有n阶导数,且
f′(x0)=f″(x0)=…=f(n-1)(x0)=0,f(n)(x0)≠0,
则当n为奇数时,x0不是f(x)的极值点;当n为偶数时,x0是f(x)的极值点,此时,若f(n)(x0)>0,则x0是f(x)的极小值点,若f(n)(x0)<0,则x0是f(x)的极大值点.
上述泰勒公式解决极值问题的方法理论意义大于实际意义,主要原因是对于一般函数求n阶导数是比较困难的,特别是对于复合函数求n阶导数.本文的出发点即是为了解决这一难题.通过引入广义导数与导数指标的概念,利用它们给出判断函数极值的充分必要条件,并利用等价无穷小的思想,来提供简便的算法.最后,通过实例说明,当第一充分性定理与第二充分定理的条件都不满足的情况下,本文的方法能够给出极值问题的判定.
本文的结构如下:第1节中给出等价关系的严格定义,并证明等价无穷小与同阶无穷小都是等价关系.第2节引入广义导数的概念,研究它的基本性质,揭示它与高阶导数之间的关系,并利用等价无穷小的方法来提供广义导数的简便计算方法.在第3节中,通过广义导数,引入导数指标的概念,给出它的等价刻画,并证明导数指标可以作为同阶无穷小的完全不变量,即两个函数是同阶无穷小当且仅当它们的导数指标相等.第4节提供了函数极值问题判定的一个充分必要条件.证明了函数在一个点处取极值当且仅当它的导数指标为偶数,并利用广义导数的符号给出极大值与极小值的判定方法.通过例子说明,当第一充分性定理与第二充分性定理的条件都不满足的情况下,本文的判别方法依然有效.
1 等价关系
定义1设S是一个集合,T是S×S的子集.则称T定义了S的一个二元关系,记为~.具体说来,对于任意(x,y)∈S×S,若(x,y)∈T,则称x和y有关系,记为x~y;若(x,y)∉T,则称x和y没有关系.
注 设T定义了集合S的一个二元关系,则对于任意的x,y∈S,或者它们有关系,或者没有关系,两者必居其一且只居其一.
定义2集合S的一个二元关系“~”称为S的一个等价关系,如果满足:
(i) 反身性:对于任意的x∈S,有x~x;
(ii) 对称性:对于任意的x,y∈S,若x~y,则y~x;
(iii) 传递性:对于任意的x,y,z∈S,若x~y,y~z,则x~z.
通过等价关系,可以将集合S中的元素进行分类,互相等价的元素构成一个等价类,它们将集合S划分成互不相交的子集合的并.对S进行等价分类的意义在于,将对集合S的研究转化为对S的子集合(等价类)的研究,化大为小;进一步,掌握每个等价类中的代表元,将对等价类的研究转化成对代表元的研究.寻找等价关系下的完全不变量,通过不变量来区分不同的等价类,是等价关系研究过程中的一个重要课题.
下面回顾实数域上的函数之间的同阶无穷小与等价无穷小的概念,并证明它们都是等价关系.以下所有的函数都是指实数域上的函数.
定义3如果函数f(x)当x→x0时的极限为0,则称f(x)为当x→x0时的无穷小.
定义4设f(x),g(x)都是当x→x0时的无穷小.
命题1同阶无穷小与等价无穷小都是等价关系.
证显然,同阶无穷小与等价无穷小分别定义了实数域上函数之间的两种二元关系.下面只证明同阶无穷小是等价关系,关于等价无穷小的证明类似.为此需要分别验证反身性、对称性与传递性.
设f(x),g(x),h(x)均为当x→x0时的无穷小.
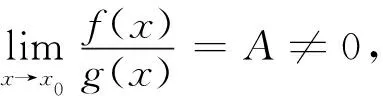
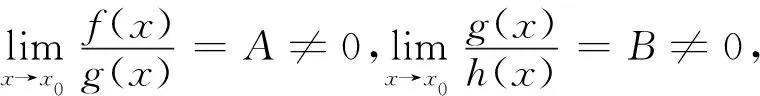
即f(x)≈h(x).
2 广义导数
本节将经典的导数概念进行推广,定义广义导数,研究它的基本性质,建立它与经典的高阶导数之间的联系,并通过等价无穷小的思想给出广义导数的简单计算方法.
从现在开始,总假定x0是函数f(x)定义域中的点,并且f(x)在x0点连续.
定义5设n是正整数,x0是函数f(x)定义域中的点.若极限

根据定义,当n=1时,广义1-导数即为经典的导数,因此,广义n-导数是经典导数定义的推广.
命题2假设存在正整数n,使得f(x)在x0点的广义n-导数存在,则f(x)在x0点连续且可导.
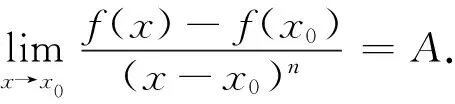
从而
这说明f(x)在x0点连续.
下面证明f(x)在x0点可导.当n=1时,显然f′(x0)=A.当n>1时,
从而f(x)在x0可导.
命题3若f(x)在x0点的n阶导数存在且连续,且f(k)(x0)=0(1≤k 证由假设,可以连续使用洛必达法则,从而得到 例1设f(x)=xn,则 (i) 在x0=0点,f(x)的广义m-导数为 证(i) 可由定义直接得到. 下面证明(ii).根据定义,有 命题4设f(x)与g(x)在x0点处存在广义n-导数,则 证(i) 根据定义与极限性质可知 从上面的命题可以看出,广义n-导数与通常的n阶导数具有密切的联系,理论上可以通过高阶导数来计算广义n-导数.但是,通常情况下,要计算n阶导数是一件很困难的事情,特别是对复合函数计算高阶导数.下面利用等价无穷小的思想来给出广义n-导数的一种简单计算方法. 证由假设 解当x→0时,有等价无穷小f(x)~x2·sinx·arctanx~x4.因此,根据定理1和例1可以得到 利用广义导数,本节引入导数指标的概念,证明导数指标是同阶无穷小这一等价关系的完全不变量,即两个无穷小函数是同阶无穷小的充分必要条件是它们的导数指标相等. 证根据定义直接验证即可. 一般地,关于导数指标,有如下等价刻画,它在后续的研究中起到至关重要的作用. 命题5设函数f(x)是当x→x0时的无穷小,则DI(f,x0)=n当且仅当 f(x)=(x-x0)n·g(x), 再证充分性.由条件可知,对于任意的正整数m 当m=n时, 当m 故DI(f,x0)=n. 从命题5可以看出,若f(x)为实数域上的多项式,则它在x0点的导数指标恰好等于f(x)中一次因式x-x0的重数.因此,导数指标可以看成是因式重数的推广. 命题6设函数f(x)与g(x)在x0点的导数指标存在,则 DI(f·g,x0)=DI(f,x0)+DI(g,x0). 证设DI(f,x0)=m,DI(g,x0)=n.则由命题5知 f(x)=(x-x0)m·f1(x),g(x)=(x-x0)n·g1(x), f(x)·g(x)=(x-x0)m+n·f1(x)·g1(x). DI(f·g,x0)=m+n=DI(f,x0)+DI(g,x0). 下面的定理说明,导数指标是同阶无穷小的完全不变量. 定理2设函数f(x)与g(x)是当x→x0时的无穷小,则f(x)与g(x)是同阶无穷小当且仅当DI(f,x0)=DI(g,x0). 证设DI(f,x0)=m,DI(g,x0)=n.由命题5知 f(x)=(x-x0)m·f1(x),g(x)=(x-x0)n·g1(x), 由于等价无穷小是特殊的同阶无穷小,显然有如下推论. 推论1设f(x)与g(x)都是当x→x0时的等价无穷小,则DI(f,x0)=DI(g,x0). 下面的命题揭示了导数指标与高阶导数之间的关系. 命题7设f(x)在x0点具有n阶连续导数,则DI(f,x0)=n当且仅当f(k)(x0)=0 (1≤k 证先证必要性.设DI(f,x0)=n,则由命题5 f(x)=(x-x0)n·g(x), 当1≤k 再证充分性.对于任意的1≤k≤n,通过连续利用洛必达求导法则可得 导数在函数极值中具有重要的应用.利用导数判断函数极值的主要方法包括第一充分性定理与第二充分性定理,但是两个充分性定理的应用具有较大的局限性.第一充分性定理需要判定函数在某一个点的局部导数值的符号,而第二充分性定理仅适用于在一阶导数为0,但是二阶导数非0的情形.对于更一般的情形,目前仍然没有行之有效的方法.本节将通过导数指标给出判断函数在某一点取极值的一个充分必要条件. 注意到上述两个充分性定理判别法都只需要考虑导函数在某一点局部取值的符号,而不需要精确求出导数值.因此,通过等价无穷小的方法,将复杂函数转化为简单函数(如幂函数),通过广义导数的符号来给出极大值与极小值的判定方法. 证考虑f(x)在x0点带有佩亚诺余项的泰勒公式 根据假设,f(x)在x0点的导数指标DI(f,x0)=n,所以由命题3可知, 并且 下面根据n的奇偶性展开讨论. (i) 若n为奇数,则当x0-δ 例4设f(x)=(x-1)x2(x+1),则由命题5可知,DI(f,±1)=1,DI(f,0)=2.因此,根据定理3,x=±1不是f(x)的极值点,而x=0是f(x)的极值点. 最后,通过一个例子说明,当第一充分性定理与第二充分性定理的条件都不满足时,导数指标判定方法(定理3)仍然可以适用. 例5判断f(x)=ex2·sinx·arctanx-1在x=0处是否取极值? 解当x→0 时,有如下等价无穷小关系: f(x)~x2·sinx·arctanx~x4. 记g(x)=x4.根据推论1与例3,有DI(f,0)=DI(g,0)=4.因此,由定理3知,x=0是f(x)的极值点. 注 (i) 根据第一充分性定理,无法判断例3中函数是否取极值. 事实上,令h(x)=x2·sinx·arctanx,则 易知h(0)=0.但是当x<0时,无法判断g′(x)的符号.由于f′(x)=eh(x)·h′(x)与h′(x)在任意一点处具有相同符号.故无法根据第一充分性定理判断x=0是否为f(x)的极值点. (ii) 根据第二充分性定理,也无法判断例3中函数是否取极值. 事实上,根据Leibnitz求导法则可知,h″(x)的每一项至少含有因式x,sinx或者arctanx,因此容易得到h″(0)=0.由于 f″(x)=eh(x)·h″(x)+eh(x)·(h′(x))2, 从而由h′(0)=0=h″(0)可知,f″(0)=0.故第二充分性定理也无法确定x=0是否为f(x)的极值点. 首先将经典的导数概念进行推广,定义了广义导数,并利用等价无穷小给出广义导数的简单计算方法.其次,引入了导数指标的概念,证明了两个函数在某一点处是同阶无穷小当且仅当它们在该点处导数指标相等.特别地,等价无穷小具有相同的导数指标.最后,得出函数在某一点处取极值当且仅当导数指标为偶数的结论,并且可以根据广义导数的符号来判定极大值与极小值.因此,通过广义导数与导数指标,可以有效解决函数极值问题.进一步,通过例子说明,当第一充分性定理与第二充分性定理的条件都不满足的情况下,导数指标判断方法依然有效. 致谢作者非常感谢相关文献对本文的启发以及审稿专家提出的宝贵意见.



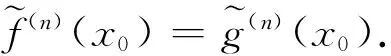

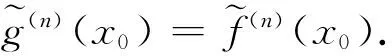

3 导数指标






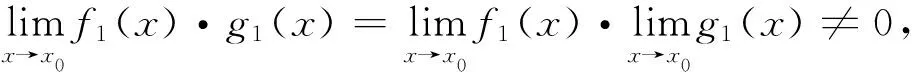

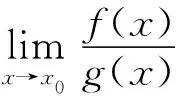



4 导数指标在极值问题中的应用




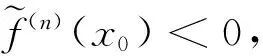

5 结 论

