复合振动筛筛分煤颗粒的离散元模拟研究

杨华瑞，马学东，赵轩瑾，王晓川，宋梅雪

(辽宁科技大学 机械工程与自动化学院，辽宁 鞍山 114013)

筛分是煤炭加工过程不可缺少的环节，振动筛被广泛应用在煤炭等散体物料的粒度分离加工领域[1，2]。目前市面上应用的传统振动筛按照振动方式主要分为直线、椭圆和圆振动筛，且技术比较成熟，其中直线振动筛应用最广[3，4]。然而学者们对于振动筛的研究一直在持续，并不断进行着创新探索。为了改善物料在筛面上的分布，解决物料堆积问题，1972年，BURSTLEIN[5]基于物料运动理论，首次提出了等厚筛，DONG等[6]使用离散元法模拟了香蕉筛的筛选过程，并研究了工艺参数对筛选性能的影响；王书林[7]等提出了异频双幅振动筛设想，即在入料端采用高频大振幅振动，出料端采用低频小振幅振动，其用意是减少振动筛入料端物料的堆积，使料层变薄变均匀，使混合颗粒体系的接触力链变弱，强化不同尺度的混合颗粒的分层；NING等[8]对摆动振动筛的颗粒分层和透筛能力进行了DEM模拟研究，发现与线性振动筛相比，摆动振动筛可以进一步获得更高的筛分效率和处理能力。上述强化筛分效果方案主要思路为变厚料层为薄料层，减小料层上部颗粒对下部颗粒的压力，使料层下部颗粒获得更大的运动，以便使混合颗粒产生更好的分层，但这种处理方式是以减少处理量为前提的；且对料层力链的破坏方式仅限于在从入料端到出料端的竖直平面内，在筛面的宽度方向对料层力链的破坏缺乏有效手段和方法。

物料筛分一般会经历入料、松散、分层、出料四个过程，物料的松散程度和分层效果直接影响着筛分的质量，传统振动筛只能给物料水平方向和竖直方向的激振力，而在筛面宽度方向并没有激振力的作用，因此物料在筛面宽度方向的运动趋势较小，物料的松散程度和分层效果还有待提高[9-11]。法国数学家Lissajous在1857年提出了振动合成理论[12]，即两个相互垂直的简谐振动可以合成为复杂的复合振动。本研究打破传统振动筛的振动方式，提出了复合振动筛，并基于Lissajous振动合成理论和空隙填充效应分析了复合振动筛的合理性；使用离散元法探究了复合振动筛在物料松散分层、筛分效率、筛分处理能力方面的优势。

1 方案设计及数理模型

1.1 方案设计

为了方便研究，以筛面长度方向为x，竖直方向为y，筛面宽度方向为z，建立全文统一的三维空间坐标系。工业上应用最早的是直线振动筛，后来为了改善物料在筛面上的运动，提高筛分效率，学者们相继提出了椭圆振动筛和圆振动筛。直线、椭圆、圆振动筛的工作方式分别如图1(a)(b)(c)所示。

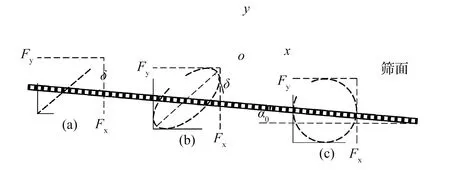
图1 传统振动筛振动方式示意Fig.1 Traditional vibrating screen vibration mode

由图1可知，传统振动筛的振动方式可以分解出沿x和y方向的激振力Fx和Fy，因此在筛面长度方向和竖直方向上对物料有松散的作用；而在z方向并没有激振力的作用，物料在筛面宽度方向上运动趋势较小，物料内部的松散效果不理想，当筛面物料较厚时，物料松散程度和分层效果还有待提高。

物料受到的激振力数量越多，物料越活跃，松散程度也就越大，分层效果越好，物料的筛分质量也就越好。基于此，如果在x和y方向激振力存在的前提下，再给物料一个沿z方向的激振力，用于物料在筛面宽度方向进行松散。在激振力的作用下，筛面会发生横向移动，筛面横向运动过程中，筛面通过摩擦力和筛丝与物料的碰撞将这个横向激振力传递给物料，使物料在筛面宽度方向上的运动趋势更大，物料内部的碰撞会更加剧烈，物料群的松散程度和分层效果会得到提高，进而提高筛分效率。除此之外，由于物料更加松散，物料在筛面的流动性也会增加，有利于排料，提高振动筛的处理能力。

1.2 数学模型

根据Lissajous振动合成理论，两个相互垂直的直线简谐振动可以在两个直线振动所构成的平面内合成复合振动，且当两个直线简谐振动的频率比或相位差不同时，可以合成不同的振动曲线[13]。

式中，S1、S2为直线简谐振动；f为振动频率；t为时间；φ为简谐振动相位。

无论是直线振动、椭圆振动还是圆振动，若按照Lissajous振动合成理论，都可以看成由两个相互垂直的直线简谐振动合成的。如图2(a)所示，当f1∶f2=1∶1时，若φ1-φ2=0则合成为倾斜的简谐直线振动；若φ1-φ2=π/2，且A1≠A2时则合成椭圆振动；若φ1-φ2=π/4，且A1=A2时则合成圆振动。当f1∶f2=2∶1时则可合成形状更为复杂的复合振动。若将图2(a)中f1∶f2=2∶1、φ1-φ2=0的复合振动图形呈一定角度放置筛面上，如图2(b)所示，筛面按照复合振动曲线运动，复合振动曲线可以分解出沿xyz三个方向的激振力Fx、Fy、Fz，则筛面呈现出较为复杂的运动状态，物料受到的激振力也更为复杂；单物料颗粒在复合振动筛上的受力如图3所示，由图1分析可知，单物料颗粒在传统振动筛上的受力不存在Fz。相比于传统振动筛，复合振动筛增加了激振力Fz，物料在筛面宽度方向受到一个激振力的作用，物料体系的整体松散程度势必会提高，从而促进物料在筛面上分层和运输。

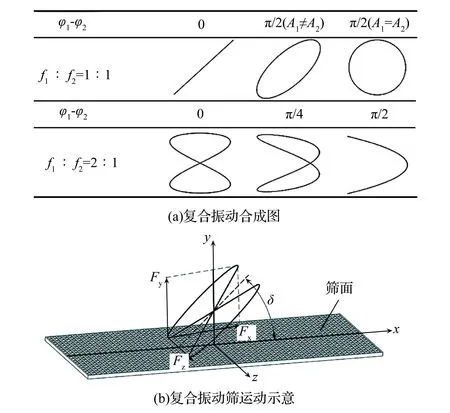
图2 复合振动曲线Fig.2 Composite vibration curve

根据Lissajous振动合成理论，给筛面添加两个相互垂直的直线简谐振动，如图4(a)所示，其中S1(频率为2f、振幅为A1)与x轴夹角为δ，S2(频率为f、振幅为A2)沿z轴方向，则S1和S2在其所构成的平面合成复合振动曲线S，复合振动S的频率为f，S1方向的振幅为A1，在S2方向的振幅为A2。

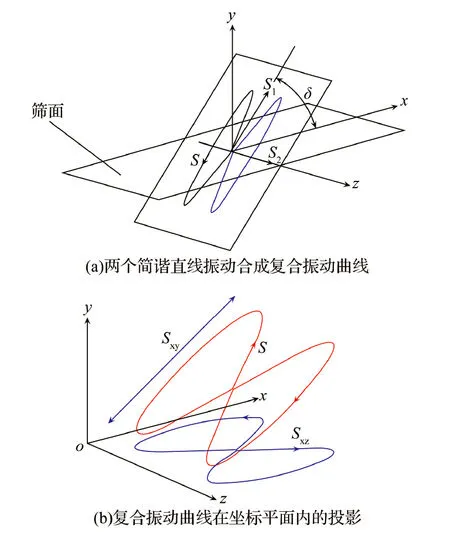
图4 复合振动曲线合成与分解效应Fig.4 Composite vibration curve synthesis and decomposition effect

如图4(b)所示，若将复合振动曲线向xoy平面和xoz平面做投影，可以得到两个分振动Sxy(频率为2f、振幅为A1)和Sxz(频率为f)。Sxy可以给物料提供一个y方向的激振力和一个x方向的激振力，y方向的激振力主要负责物料在竖直方向的松散，x方向的激振力主要负责物料向排料口运动；Sxy是筛分工作的主运动，负责物料的抛掷，其筛分原理与直线振动筛相同。Sxz是一条扭转闭合的振动曲线，可以给物料提供一个z方向的激振力和一个x方向的激振力，z方向的激振力主要负责物料在筛面宽度方向的松散，这是复合振动筛的特有之处。由于Sxz的存在物料会在筛箱内发生搅动，增大物料的松散程度，促进物料在筛面发生分层。

筛箱在xyz三个坐标轴方向上的位移曲线如图5所示，可以看出，在x方向的频率为2f，振幅为A1cosδ，在y方向的频率为2f，振幅为A1sinδ，在z方向的频率为f，振幅为A2。

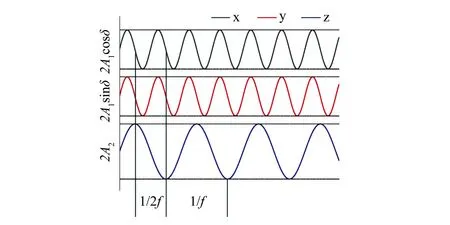
图5 复合振动曲线在xyz三个坐标轴的位移曲线Fig.5 Displacement curves of composite vibration curves in xyz three coordinate axes

1.3 物理模型

离散元模拟(DEM)将颗粒体系离散为单独的个体单元，依据颗粒材料性质的不同，使用不同的接触模型，基于牛顿第二定律进行运算。接触模型是DEM进行模拟计算的基础，模型选择的正确与否直接决定了模拟计算的可靠性，本研究使用Hertz-Mindlin(on-slip)软球接触模型[14]进行运算。颗粒在运动过程中受到重力、切向力距、法向力距和摩擦力的多重作用。由此可推知第i个颗粒的运动方程为[15]：

式中，mi为颗粒的质量，kg；Ii为颗粒所受的转动惯量，kg·m2；Vi为颗粒速度，m/s；ωi为颗粒角速度，rad/s；ri为颗粒半径尺寸，mm；Fg为重力，N；Ff为摩擦力，N；Fn，ij为颗粒所受的法向力，N；Ft，ij为颗粒所受的切向力，N；Tt，ij为颗粒所受的切向力距，N·m；Tr，ij为颗粒所受的法向力矩，N·m。

建立简单的振动筛仿真模型，由颗粒工厂、筛箱、筛网、计算域组成，如图6所示。

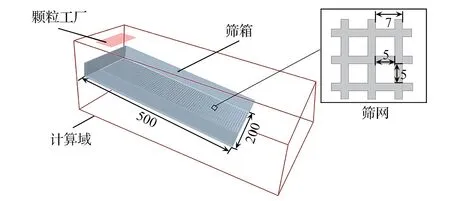
图6 振动筛仿真几何模型(mm)Fig.6 Geometric model for vibrating screen simulation

2 DEM模拟

2.1 仿真参数设置

使用煤颗粒为研究对象，筛面材料为钢，材料的物理参数和接触参数见表1[16]，总仿真时间为10 s。由于椭圆振动的长轴振幅与短轴振幅不同，且椭圆振动筛工作时长轴方向对筛分工作起决定性作用，故使用长轴方向振幅来表征椭圆振动的振幅，且长轴振幅和短轴振幅比为2∶1[17]。并且使用球型颗粒和非球型进行模拟运算取得的筛分效果并无明显区别[18]，考虑到运算成本比和时间成本，使用球型颗粒进行模拟运算。颗粒由颗粒工厂随机生成，具体数值见表2。

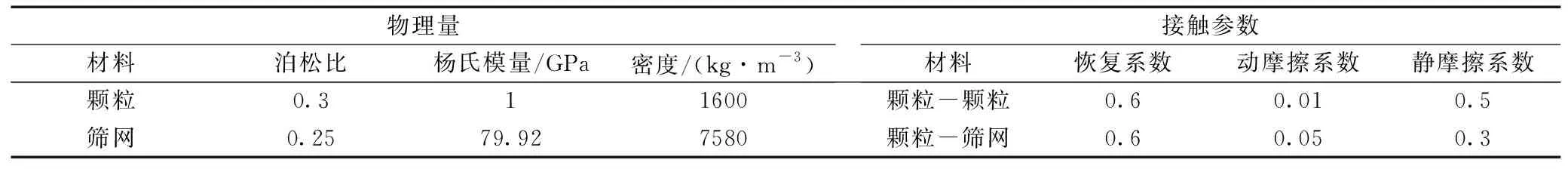
表1 材料特性Table 1 Material properties

表2 仿真参数设置Table 2 Simulation parameters

2.2 DEM仿真结果分析

将图2(a)中频率比为2∶1的三种不同相位差的复合振动曲线仿真结果进行对比，如图7所示。从图7中可以看出使用相位差为0°和相位差为45°的复合振动进行筛分时，颗粒在筛面上都能取得较好的分层效果，而颗粒在相位差为90°的复合振动筛上的分层效果并不理想。这是因为相位差为0°和45°的复合振动曲线形状相似，两者在xoz平面内的投影形状均为图4(b)所示的扭转闭合的振动曲线，可以使物料在筛箱内发生搅动；而相位差为90°的复合振动曲线在xoz平面内的投影为往复弯曲的振动曲线，无法形成扭转闭合的振动曲线。因此采用相位差为0°的复合振动筛与传统振动筛进行对比。

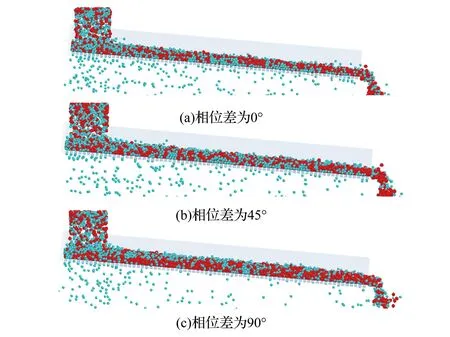
注：试验条件为f =18 Hz、A=2 mm、δ=45°、α0=5°图7 不同相位差的复合曲线筛分效果对比Fig.7 Comparison of sieving effect of composite curves with different phase differences

由图5可知筛体在z轴方向的运动为简谐直线振动，为了观察颗粒在筛面上的分布和运动情况，使用速度矢量图表征颗粒的运动，如图8(a)所示。颗粒在z轴激振力的作用下，先向左前方再向右前方交替运动，且颗粒在筛面上分布均匀。图8(b)为1～5 s颗粒在z轴方向偏离初始位置的位移曲线，可以看出颗粒在初始位置0刻度线上下波动。由图8可知颗粒在复合振动下能够在筛面上正常运动，因此复合振动的筛分的方案具有可行性。

图8 颗粒在复合振动筛筛面上的运动Fig.8 Movement of particles on the screen surface of a composite vibrating screen

截取仿真中间时刻t=5 s时的仿真图片，如图9所示，红色颗粒的粒径大于筛孔直径，蓝色颗粒的粒径小于筛孔直径。图9展示了复合、椭圆、圆、直线振动筛的筛分效果以及同一位置的局部放大情况。9图(a)中，大部分小颗粒位于料层的中下方，大颗粒位于料层的中上方，颗粒在筛面上发生了明显的分层现象，只有小部分区域没有形成有效的分层。与筛面接触的颗粒以小颗粒为主，有利于小颗粒穿透筛网完成筛分工作，从图9中筛网下方的颗粒数量也能看出，复合振动筛筛网下方颗粒的密集程度明显大于其他三种振动筛，由此也可以说明复合振动筛的透筛率更高。反观图9(b)(c)(d)三种传统振动筛，在筛面上呈现出大小颗粒混杂的状态，不利于小颗粒穿透筛网。

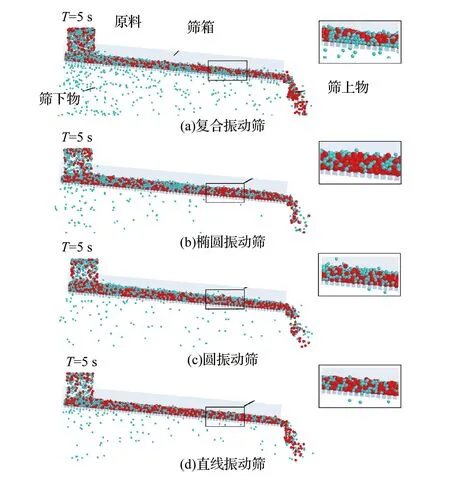
注：振动参数均为f=18 Hz、A=2 mm、δ=45°、α0=5°图9 筛分效果Fig.9 Screening effect diagram

复合振动由于存在沿z轴方向的分振动，会给颗粒一个沿z轴的力。提取整个仿真过程中颗粒在z轴方向的受力，如图10(a)所示，可以看出复合振动下颗粒在z轴方向的受力远远大于其他三种振动，且力的方向呈周期性变化；传统振动筛的三种振动模式下，颗粒也会产生沿z轴方向的力，但是这个力不是由筛网提供的，而是由于颗粒之间的不规则碰撞产生的沿z轴方向的切向力；因为由碰撞产生的力较小，对颗粒体系的影响较小，所以在宏观上体现不出明显效果，即没有形成有效地分层。

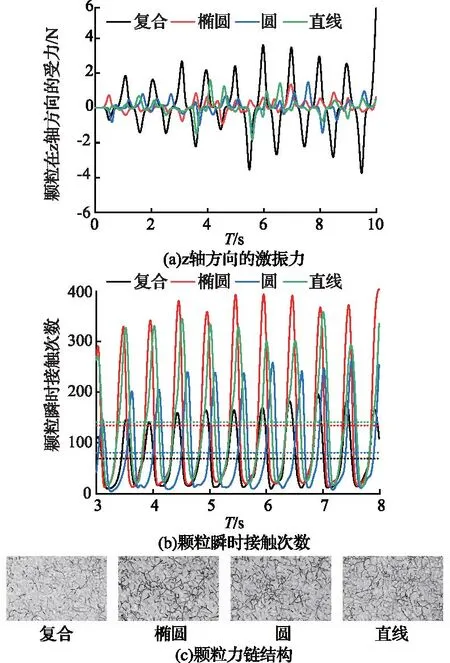
注：试验条件为f=18 Hz、A=2 mm、δ=45°、α0=5°图10 试验数据分析Fig.10 Experimental data analysis

为了量化颗粒体系的松散程度，引入颗粒之间的接触次数，颗粒与颗粒的接触次数越少，说明颗粒之间的空隙越大，颗粒体系的松散程度越大；反之，内部颗粒自由活动的空间越小，松散程度越小。提取仿真过程中3～8 s颗粒的瞬时平均接触次数，如图10(b)所示，复合、椭圆、圆和直线振动分别为68.96、134.22、80.67、140.77。复合振动筛筛面上颗粒的瞬时接触次数低于其他三种传统振动筛。

提取相同时刻(T=5 s)的颗粒间力链结构，如图10(c)所示，图中黑色和灰色短键代表颗粒间法向接触力的大小，短键颜色越深，法相接触力越大，相互连接后形成强力链；短键颜色越浅，法相接触力越小，相互连接后形成弱力链[19，20]。强力链越多说明颗粒内部越稳定，抵抗外部干扰的能力越强，颗粒更容易表现出固体性质，流动性弱；强力链越少，颗粒之间相互作用越弱，颗粒更容易表现出流体性质，流动性强。从图中可以看出，颗粒在复合振动筛上形成的力链绝大多数为弱力链。

通过以上分析可知，复合振动筛相比于传统振动筛增加了一个沿z轴方向的激振力Fz，则颗粒在复合振动筛筛面的会受到Fx、Fy、Fz三个激振力的作用，颗粒受力更加复杂，内部碰撞更加剧烈，可有效打破颗粒之间的力链结构，使颗粒体系松散程度增大，自由活动空间更大，有利于形成分层，增加小颗粒的透筛率，提高筛分效率。

为了探究不同振动参数(频率、振幅和振动方向角)对复合振动筛筛分效果的影响，对每个参数进行了单因素试验，并且在相同的参数条件下设置了传统振动筛对比试验。探讨了四种振动筛在不同振动参数下的筛分效率和运输处理量(处理量用颗粒在x方向的速度表征)，其中筛分效率的计算由公式(4)得出。筛分质量使用筛分效率η来衡量，η也就越大，说明筛分质量越高。η定义为[21]：

式中，α、θ、β分别为原料、筛上物和筛下物中粒径小于筛孔直径的物料含量，%。

各种变量取值见表3，试验结果如图11所示。由图11可以看出，当频率处于18～19.5 Hz，振动方向角处于30°～35°，振幅处于2～3 mm，复合振动筛的筛分效率高于直线振动筛、圆振动筛、椭圆振动筛的筛分效率；在不同振动参数下复合振动筛颗粒在x轴方向的输送物料的速度均高于直线振动筛、圆振动筛、椭圆振动筛的输送物料速度。因此，相比于传统振动筛，复合振动筛在筛分效率和物料处理量两方面都具有较大优势。

表3 振动参数单因素实验Table 3 Single factor experiment table of vibration parameters

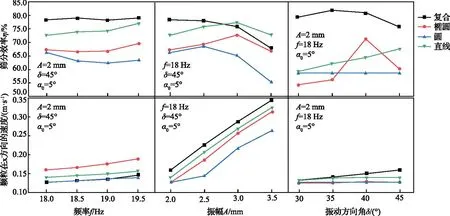
图11 振动参数对筛分效果的影响Fig.11 Influence of vibration parameters on screening effect

3 结 论

1)将复合振动分别向xoy平面和xoz平面做投影可以得到两个分振动，其中xoy平面的分振动为直线简谐振动，负责物料的抛掷运输，其工作原理与直线振动筛相同；xoz平面内的分振动主要负责物料在筛面宽度方向上进行松散，提高颗粒体系的松散程度，强化分层效果。

2)离散元模拟验证表明，相对于传统振动筛，复合振动筛可以给物料提供沿筛面宽度方向的激振力，物料受到沿xyz三个方向激振力的作用，受力更加多样化，松散程度大，分层效果好，筛分效率高。

3)相比于传统振动筛，复合振动筛在筛分效率和物料处理量两方面都具有较大优势。

4)复合振动筛对力链结构的破坏能力强于传统振动筛，有利于混合颗粒体系的松散，在含水物料和厚料层物料筛分中具有较大优势。