圆管带式输送机桁架结构轻量化设计

周利东，展翼飞，袁 媛，闫永杰，刘 源，张鼎益，陈振鲁

(1.太原科技大学 机械工程学院，山西 太原 030024；2.太重集团向明智能装备股份有限公司，山西 太原 030032)

随着高效绿色发展不断深入，长距离、大运量和更加复杂灵活的线路布置成为圆管带式输送机发展趋势[1]。桁架和支腿是圆管带式输送机的主要承载结构，约占总成本的三分之一，而长距离和大运量意味着数目和成本进一步增加。然而，对于圆管带式输送机桁架结构的型材选择，技术人员常参照已有案例设计，导致结构过重，造成钢材浪费。因此，在满足圆管带式输送机长距离、大运量等功能需求的同时如何尽可能地降低钢结构成本，成为设计时不得不面临的难题。为符合绿色发展的要求，对圆管带式输送机桁架结构进行轻量化设计十分必要。

针对圆管带式输送机桁架结构的轻量化设计，已有广泛的研究。Horak[2]提出了一种圆管带式输送机托辊窗板的改进方法，在分析了传统槽形带式输送机和管状带式输送机托辊的布置特点之后，提出了一种倒“U”型截面的窗板。随后，提出了一种三角形桁架，较典型的矩形截面桁架更节省钢材[3]。在杆件截面优化方面，樊涛[4，5]等利用APDL语言实现桁架模型的参数化分析，并基于满应力优化准则，以结构质量为优化目标，以杆件截面面积为设计变量对桁架各杆件进行优化；LIU[6]用Ansys软件分析得到了一段圆管带式输送机桁架梁结构的等效应力图和轴力图；吴炳胜、周明峰[7，8]等利用Ansys Workbench仿真平台对圆管带式输送机桁架进行有限元分析，并使用优化工具箱对杆件截面进行优化；宋俨轩[9]等在Ansys Workbench仿真平台中对一段桁架应力最大杆件截面进行响应曲面分析和目标驱动优化分析，对截面角钢进行尺寸结构优化。

已有的研究大部分采用了Ansys Workbench对圆管带式输送机桁架结构[10]进行静态有限元分析，并对杆件截面进行了优化。传统研究大部分并未分析桁架的荷载组合，所以得到的结果是桁架在单一工况下的有限元结果；且基于DoE实验设计理论分析和设计优化过程研究得较少。本文将圆管带式输送机桁架作为一种工业建筑结构，在进行静态分析时，基于建筑结构荷载的有关规范对承受的荷载进行计算和组合；同时对桁架不同类型的杆件截面尺寸进行优化设计时，基于DoE实验设计理论优化设计[11]流程和效率。

1 桁架结构的静态分析

1.1 荷载分析

圆管带式输送机常安装于户外[12]，其桁架结构除了承受输送物料的重量外，还承受风载、雪载及温度作用。这些荷载往往多种同时作用于结构，导致荷载情况多种多样。因此，在桁架静态分析之前，必须对荷载进行分析和组合。圆管带式输送机桁架结构是一种典型的工业建筑结构[13]，其荷载可以参考工程结构荷载与可靠度设计原理[14]及有关规范进行计算与组合。建筑结构的荷载可分为三类：永久荷载、可变荷载、偶然荷载。对于圆管带式输送机桁架结构而言，永久荷载包括桁架自重+托辊重量+输送带重量+物料重量；可变荷载包括桁架两侧走台的楼面活荷载、风荷载、雪荷载及温度作用；偶然荷载包括地震作用等。

荷载基本组合的效应设计值Sd，可从式(1)和(2)算得的组合效应设计值中，取最不利荷载组合进行确定[15]。由可变荷载控制的效应设计值，应按式(1)计算：

由永久荷载控制的效应设计值为：

式中，γGj为第j个永久荷载的分项系数；γQi为第i个可变荷载的分项系数；γLi为第i个可变荷载考虑设计使用年限的调整系数，其中γL1为主导可变荷载Q1考虑设计使用年限的调整系数；SGjk为按第j个永久荷载标准值Gjk计算的荷载效应值；SQik为按第i个可变荷载标准值Qik计算的荷载效应值，其中SQ1k为诸可变荷载效应中起控制作用者；ψci为第i个可变荷载Qi的组合值系数；m为参与组合的永久荷载数；n为参与组合的可变荷载数。

荷载偶然组合的效应设计值Sd可按下列规定采用：用于承载能力极限状态计算的效应设计值，应按式(3)计算：

式中，SAd为按偶然荷载标准值Ad计算的荷载效应值；ψf1为第1个可变荷载的频遇值系数；ψqi为第i个可变荷载的准永久值系数。

用于偶然事件发生后受损结构整体稳固性验算的效应设计值，应按式(4)计算：

应注意的是，组合中的设计值仅适用于荷载与荷载效应为线性的情况。

1.2 模型建立及荷载施加

由于桁架结构的荷载组合复杂多样，导致杆件内力计算量巨大，常采用电算。在本文中，首先通过Ansys workbench对桁架梁进行静力学分析。该桁架跨度为30.4 m，属于整机结构中跨度最长的一段桁架(除尾部栈桥结构外)，相对位置如图1(a)所示。与普通桁架不同的是，圆管带式输送机桁架节间的断面为窗板，横向剖面如图1(b)所示。桁架高为1.35 m，中间节间距为1.5 m，截面宽度为0.65 m，桁架的纵向示意如图2所示。初步选用的杆件型材及材料属性如下：弦杆为L100×8，B8；斜杆(斜横腹)为L70×5；型钢材料为Q235-A；弹性模量E=2.06×105N/mm2；泊松比μ=0.30；质量密度ρ=7850 kg/m3。此外窗板厚度为5 mm。

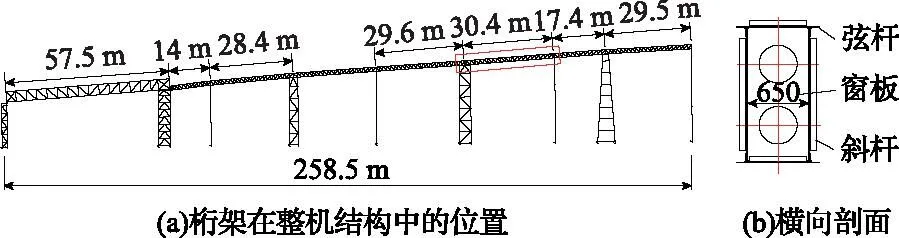
图1 桁架在整机结构中的位置及桁架结构横向剖面(m)Fig.1 Position of the truss in the structure of the whole machine and transverse section of the truss

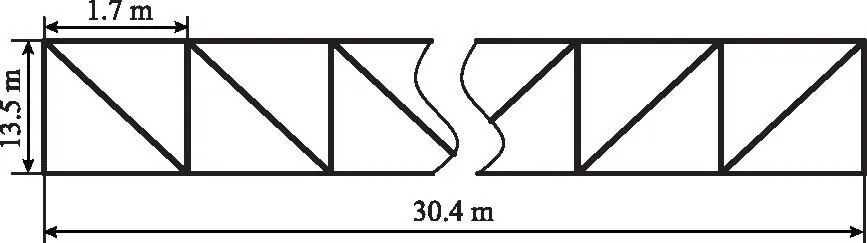
图2 桁架结构纵向示意Fig.2 Longitudinal schematic diagram of the truss structure

计算桁架内力时，通常假定荷载作用线通过桁架的节点[16]，所以本文将各类型荷载均以节点荷载的形式施加于桁架节点之上，荷载施加情况如下：恒载为2.5 kN/m；活载为2.5 kN/m2；风载为0.4 kN/m2；雪载为0.4 kN/m2。另外，本文采用桁架一端固定，一端铰接的约束方式，桁架的有限元模型如图3所示。

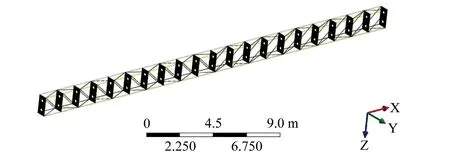
图3 桁架的有限元模型Fig.3 Finite element model of the truss

1.3 分析结果

根据荷载分析和圆管带式输送机常见的荷载可知，桁架应有如下荷载基本组合：①1.2恒载+1.4活载；②1.2恒载+1.4雪载；③1.2恒载+1.4风载；④1.35恒载+1.4×0.8活载+1.4×0.6风载；⑤1.35恒载+1.4×0.8活载+1.4×0.6雪载；⑥1.2恒载+1.4×0.9活载+1.4×0.9风载；⑦1.2恒载+1.4×0.9活载+1.4×0.9雪载。

通过Ansys的计算得到，桁架的最不利荷载组合应为组合④，桁架的等效应力和位移如图4、图5所示。从图中可以看出，各类型杆件的最大组合内力和最大变形分别位于中部下弦杆、两端斜杆位置处，因此这几处杆件最危险，优化设计时需重点考虑。

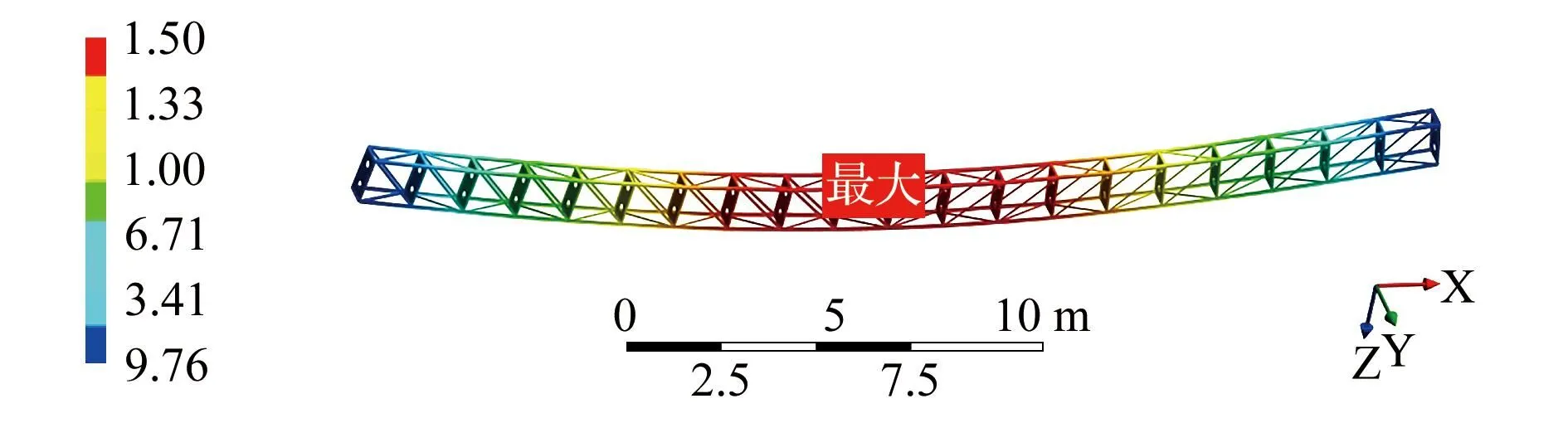
图4 桁架最不利荷载组合下的等效应力(MPa)Fig.4 Equivalent stress diagram for the most unfavourable loading combination of the trusses

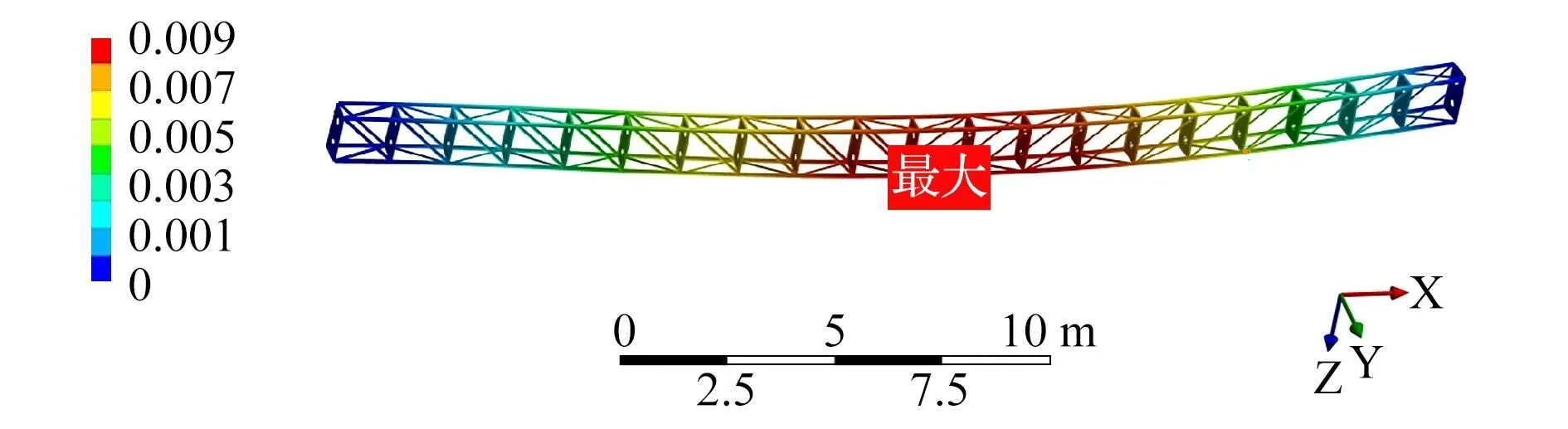
图5 桁架最不利荷载组合下的位移(mm)Fig.5 Displacement of the truss under the most unfavourable load combination

另外，通过3D3S软件计算统计弦杆、斜杆(斜横腹)这两种杆件的应力比发现，应力比小于0.5的杆件数量总计接近50%。同时，跨中应力最大值为149.8 MPa，位移最大值为9.3 mm，小于规范[17]要求的许用应力和挠度(L/400，L为桁架跨度)。说明该桁架型材截面使用不充分，存在优化空间。其中，各类型杆件应力比统计见表1。

表1 应力比小于0.5的杆件数量占比Table 1 Percentage of number of bars with stress ratios less than 0.5

2 基于DoE的桁架结构多目标优化分析

DoE-实验设计(Design of Experiments)[18]是研究正确的设计实验计划和分析实验数据的理论和方法，其本质是运用数学方法，科学合理地安排实验方案，可以在保证实验可靠性的基础上大大降低实验的规模和时间。桁架结构在轻量化设计时受强度、刚度等因素制约，属于多目标优化的范畴。采用DoE方法进行数据处理和优化设计，可提高计算效率，优化设计过程[16]。

2.1 确定设计变量、约束及目标函数

结合1.3的分析结果，选取桁架弦杆、斜杆(斜横腹)的宽度和厚度以及窗板的厚度作为设计变量，如图6所示；以弦杆中部的位移和最大等效应力作为约束条件；以弦杆、斜杆和竖杆的质量最小作为目标函数。由此可得桁架轻量化的数学模型，见式(5)。

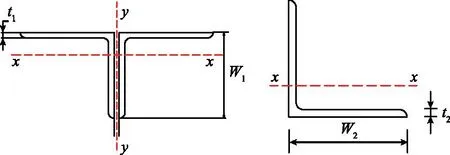
图6 各类型杆件截面的设计变量Fig.6 Design variables for each type of bar section

式(5)中，W1、t1、M1分别为弦杆双角钢的宽度、厚度和质量；W2、t2、M2分别为斜杆(斜横腹)角钢的宽度、厚度和质量；t3、M3分别为窗板的厚度和质量；σmax为最大等效应力值；wmax为最大变形量。其中宽度和厚度的单位均为m，质量的单位为kg。

2.2 参数相关性分析

在DoE实验中，参数关联性分析通过研究输入参数对输出参数的敏感性，可以筛选出主要控制参数和次要控制参数，即筛选出对优化目标敏感度更高的设计变量。可以节省实验成本。如图7所示，为选取的输入参数对输出参数敏感性分析。

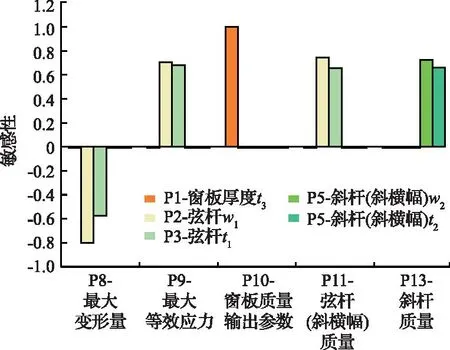
图7 设计参数敏感性Fig.7 Sensitivity of the design parameters

从图7中可以看出，弦杆角钢截面的宽度W1和厚度t1对最大变形量和最大组合应力的敏感性相关值超过了0.5或接近0.5，说明其影响力较大。对弦杆、斜杆(斜横腹)和窗板的质量影响较大的分别是其截面的宽度和厚度。

2.3 响应面模型的构造及分析

在DoE实验中常使用近似模型中的响应面方法，通过数量较少的特征样本点仿真计算拟合出连续的响应曲面。合适的响应面模型可显著提升后续寻优计算的有效性，也可以较为准确地反映出输入与输出参数之间的关系[19]。

首先，基于前文参数相关性分析得到的输入参数与输出参数的分析结果，及响应面模型的精确度和优化计算的效率的综合考虑下，选用拉丁超立方体抽样方法生成设计点，利用Ansys workbench中的Response Surface Optimization模块制定仿真计算方案。生成的样本设计点见表2。

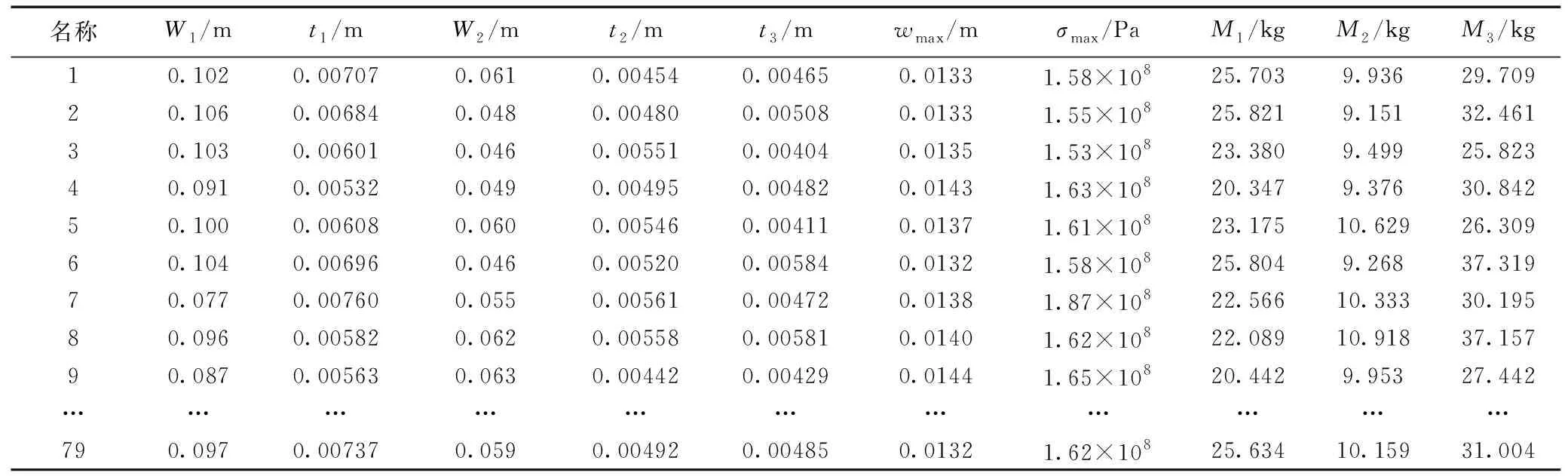
表2 实验样本设计点Table 2 Design points of the samples

为了使采样点具有分布均匀性，采用拉丁超立方抽样方法；该方法在设定的集合内随机采取一个样本点，能够有效避免样本点的坍塌现象，同时具有较强的空间填充能力和不可重复性，在拟合二阶或高阶非线性的性能方面较强。

拉丁超立方抽样可描述为在N维向量空间中抽取Q个0到1之间的均匀样本数据，分别采用N×Q的矩阵A、B来存储样本坐标。以桁架型材截面的6个设计变量(W1、t1、W2、t2、t3)作为输入变量；对应的，以最大变形量wmax、最大等效应力σmax、弦杆质量M1、斜杆(斜横腹)质量M2、窗板质量M3作为响应值。设置样本类型为CCD，生成样本数为79，通过计算求解，获得样本数据及对应的响应值见表2。

接着，考虑本文研究问题的特点和样本空间的规模，采用具有稳健性高、模型精度高及可避免噪音点干扰等优点的非参数回归方法，实现对输出量的响应面拟合，建立响应面模型如图8所示。

图8 响应面模型Fig.8 Response surface model

图9 设计变量对目标函数的灵敏度Fig.9 Sensitivity of design variables to the objective function

2.4 多目标优化

本文选用多目标遗传算法(MOGA)优化方案，MOGA是基于受控精英概念的流行NSGA-Ⅱ(非支配排序遗传算法Ⅱ)的变体。该方案支持多个目标和约束，具有良好的全局搜索功能，且不需要复杂的辅助信息就可以进行求解等优点。通过Ansys Workbench中的Response Surface Optimization模块生成MOGA算法优化方案，初始样本数为4000，每次迭代的样本数为800，最大允许帕累托百分比为70，最大迭代次数为20，得到3个候选样本。

通过对优化得到的3组候选点进行有限元计算，将计算结果与优化解进行对比，得到的误差很小，在工程应用中可忽略不计，见表3。

表3 优化候选点验证Table 3 Validation of the optimized candidate points

从3个样本候选点中选出最合适的一个，对设计变量圆整以便对应型钢的型号，与优化前进行对比，见表4。从表4中可以看出，桁架结构优化后，总体质量减轻了1611.224 kg，较现有桁架减轻32.8%；另外，虽然最大组合应力和最大位移量有所增加，但仍在强度和刚度允许范围内；同时各杆件应力比小于0.5的数量占比下降了16.25%，说明杆件截面较优化前使用更加充分。

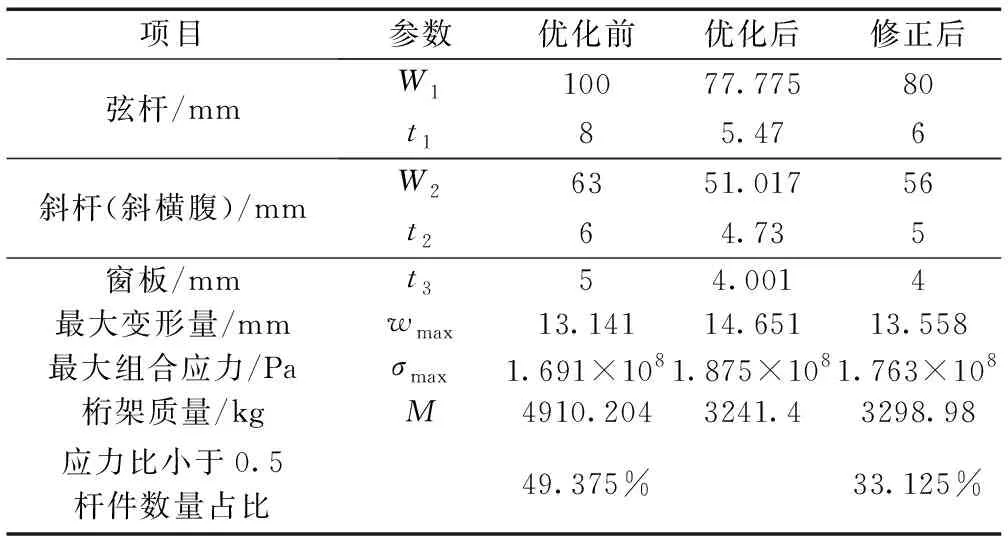
表4 桁架结构优化前后结果对比Table 4 Comparison of results before and after the truss structure optimization

3 结 论

1)基于建筑结构的有关规范，准确分析了圆管带式输送机桁架结构承受的荷载组合情况；并在3D3S软件中对其进行静态分析，正确地得到了桁架杆件最大组合内力的分布情况。

2)基于DoE实验方法对桁架各类型杆件截面进行优化研究，实现了桁架结构整体轻量化。通过拉丁超立方抽样和非参数回归方法建立了响应面模型，能够准确且合理地描述输入与输出参数之间的关系，为优化计算奠定基础；通过多目标遗传算法进行优化计算，优化后，桁架整体质量减轻32.8%，同时各杆件各应力比均有所提高，杆件截面使用更加充分。然而，实际的角钢截面尺寸是离散的序列值；因此，有必要将桁架主要型材的截面作为离散变量，采用离散变量优化算法对桁架进行轻量化研究，使优化结果更具有应用价值。