弛张筛面动态特性数值模拟及参数优化

武继达，刘初升，王振乾，江海深，邹梦麒，邱文强



弛张筛面动态特性数值模拟及参数优化

武继达1，刘初升1，王振乾1，江海深2，邹梦麒1，邱文强1

(1. 中国矿业大学 机电工程学院，江苏 徐州，221116；2. 中国矿业大学 化工学院，江苏 徐州，221116)

针对弛张筛筛面破损问题，考虑筛面的装配形式和工况条件，建立实际安装状态下的筛面有限元分析模型，分析工作条件下筛面不同位置的变形及应力分布；将响应面法与优化技术相结合，以安装半径和弯折角度为设计变量，通过中心复合试验设计，构建反映筛面设计参数与筛面应力关系的二阶响应面近似模型，分析各设计变量对筛面工作应力的影响规律；结合目标规划优化方法和NSGA-Ⅱ遗传算法对响应面近似模型进行寻优，获得筛面最佳几何参数。研究结果表明：筛面剪切应力主要分布在弯折区域中心部位；优化后，当弯折半径为22.5 mm，弯折角度为150°时，筛面剪切应力取得最小值，并较初始值降低12.6%。

筛面；数值模拟；试验设计；响应面法；子模型；参数优化

近年来，随着煤炭产业政策的调整和大气污染防治的需要，动力煤的洗选比例不断提高，洗选下限不断降低[1−3]。弛张筛作为一种新型筛分设备，以其筛分效率高、不易堵塞、适用于细黏湿物料等特点被广泛应用于潮湿细粒煤炭的深度干法筛分领域[4−6]。聚氨酯筛面是弛张筛的重要工作部件，筛面的可靠性对于弛张筛的工作连续性具有重要意义。由于弛张筛筛面工作时需反复承受高频挠曲变形，受力复杂，故其寿命往往比一般振动筛筛面的低。因此，有必要对聚氨酯筛面进行分析和改进设计，在满足工作要求的情况下，尽量降低其工作应力，提高使用寿命。目前，针对弛张筛筛面的研究主要集中在筛面运动特性分析及工艺参数优化，针对其工作条件下的力学分析较少。彭利平等[6]基于细长压杆模型，通过理论和实验相结合的方法，分析了弛张筛面大挠度非线性变形特性；翟宏新等[7−8]系统地考虑弛张筛的结构、工艺、动力学和运动学参数，提出以综合评价指数作为优化目标，提高了弛张筛的运行效率；董海林等[10]从改变筛面约束的角度出发，提出了一种半圆式支撑横梁结构，以降低筛面的平均等效应力；王新文等[11]基于有限元静力学分析，对比了螺栓配合式和卡槽嵌入式2种固定方式对筛面应力分布的影响。但上述研究仅针对平直筛面进行仿真分析，未考虑到筛面的实际安装特点，模型不能完全反映筛面的实际变形及受力情况。本文作者针对筛面安装特点，改进筛面有限元分析模型，对比分析筛面不同区域的运动特性，结合参数化建模和响应面设计理论，建立筛面设计参数与性能参数之间的近似模型，并利用遗传算法对设计参数进行寻优，以期降低筛面工作应力，提高筛面使用寿命。

1 筛面有限元模型

1.1 筛面安装特点及建模

由于弛张筛工作原理的特殊性，筛面运动形式与一般振动筛有较大区别，借助于弹性筛面的弛张挠曲，弛张筛可以依靠较小的筛体运动实现较大的筛面振幅[12]。换言之，筛面与筛体运动并不一致，为防止被筛分物料沿筛面与筛体侧面的间隙漏下，弛张筛筛面在与筛体侧面接触的部分往往以一定半径向上弯折若干角度，如图1所示。实际运行表明，该设计对聚氨酯筛面工作性能以及工作寿命都有一定的影响。

1—聚氨酯筛面；2—筛面安装梁；3—筛面弯折区域；4—筛体侧板。

根据聚氨酯筛面实际尺寸，利用三维建模软件Creo建立筛面模型，考虑到筛面的几何对称性，选取筛面实际外形的一半进行建模，模型长×宽×高为880 mm×310 mm×4 mm，筛孔长×宽为13 mm× 13 mm，筛面两侧及与侧板接触部分各自留有宽度为40~50 mm的盲板。为更好地贴合实际，利用Creo“骨架折弯”功能模拟筛面与侧板接触部分的弯曲情况，折弯后的张弛筛筛面模型如图2所示。为便于后续优化，折弯的弯折角度和半径均进行参数化处理。初始弯折角度=120°，弯曲半径=30 mm。建模完成后，利用与有限元分析软件AWB DS(ANSYS workbench design simulation)的接口，将模型导入并进行后续有限元分析。

图2 弛张筛筛面三维模型

1.2 确定材料参数

弛张筛筛面采用聚氨酯弹性体材料制成，属于不可压缩的超弹性材料，其物理特征如下：在较小的应力作用下可以产生较大的变形。对于这类材料，在大变形条件下，通常不定义弹性模量，而是利用本构模型描述其应力−应变本构关系。常用的超弹性体本构模型主要有Mooney-Rivlin模型、Neo-Hookean模型、Ogden模型、Yeoh模型、Peng-Landel模型等。本文采用两自由度的Mooney-Rivlin模型模拟筛面材料，当拉应变不超过100%，压应变不超过30%时，此模型可以很好地描述超弹性体材料的力学性能。Mooney-Rivlin模型的两参数表达式为

式中：为应变能密度；10和01均为材料常数；1和2分别为一阶和二阶应变不变量，是主拉伸比的函数，且满足如下关系：

为确定Mooney-Rivlin模型的材料常数，通常可采用硬度指标经验公式[13]计算，聚氨酯筛面弹性模量与邵氏硬度的关系可近似表示为

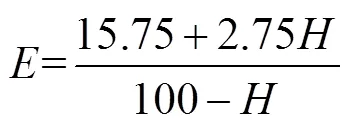
利用硬度计测量实际聚氨酯筛面硬度，多次测量后取平均值，得到聚氨酯筛面邵氏硬度=88.6，代入式(3)得聚氨酯材料弹性模量为18.09 MPa。参考文献[9]中的方法，令=2(10+01)，且≈3，01=0.2510，则可以分别计算出仿真所需Mooney-Rivlin模型的材料常数10=2.412 MPa，01=0.603 MPa。

1.3 网格划分及边界条件

基于参数化的三维模型和本文1.2节中计算所得的材料本构模型参数，利用ANSYS Workbench建立筛面有限元分析模型，采用扫略法划分网格，共划分134 905个单元，250 297个节点，如图3所示。

工作过程中，弛张筛筛面载荷可分为物料自重引起的均布载荷和被抛掷物料对筛面产生的冲击载荷。本文参考文献[14]和[15]中的处理方式，将筛面载荷等效于施加于筛面表面的正压力。单片筛面承受的正压力为

为模拟实际工作过程中的工况，在筛面两端分别施加水平方向的正弦位移激励1和2，定义主筛体与浮动筛框振幅均为6 mm，并考虑到筛面松弛安装，最终位移激励形式为

式中：为工作时间。

约束其他方向上的自由度，为便于计算收敛，开启惯性释放，将位移激励分为100个子步施加。

图3 弛张筛筛面的有限元模型网格划分

2 筛面的变形和应力结果分析

2.1 筛面整体变形分析

对筛面模型进行有限元计算，获得筛面模型的最大变形时刻的变形云图，如图4所示。由图4可以看出：在筛面两端施加6 mm的位移激励后，筛面产生明显的挠曲变形。中点区域最大变形量为38.824 mm，且挠曲程度由中间向两侧逐渐递减。与此同时，筛孔尺寸发生变化，平行于位移方向上的筛孔受到挤压弯曲，弯曲变形量在孔的中心达到最大值；在垂直于位移的方向上筛孔被拉长。这种周期性的变形有利于破坏细粒物料的黏附，实现筛面的自清理，保护筛面的通透性。

图4 筛面的变形云图

筛面挠度是衡量弛张筛工作能力的重要指标之一。根据文献[15−17]中的筛面变形公式，筛面中点挠度的理论计算公式为

式中：为筛面中点挠度；为筛面参与运动的长度；为固定梁与浮动梁横梁间距。

将筛面有限元模型的几何参数代入式(5)，得到筛面中点最大挠度的理论值为max=36.986 mm。

结合图4中的仿真结果可知筛面中点最大挠度理论值与仿真值的相对误差为4.7%，小于5%，说明有限元模型简化合理，网格划分的精度满足计算要求，边界条件设置符合筛面实际工况，最终变形计算结果是可信的。

式(5)仅计算了筛面中点的最大挠度，而由图4可以看出：筛面实际工作条件中各个位置挠度并不完全一致。为此，利用单元路径映射功能，分别提取筛面1−2，1−2和1−2这3处位置的挠度，其中1−2处为筛面弯折的圆弧中点，1−2和1−2在距离上关于1−2对称，映射路径具体位置如图5所示。筛面不同位置的挠度−位置曲线如图6所示。从图6可以看出：筛面挠度关于筛面几何中心线呈对称分布，筛面弯折部分1−2处的挠度明显小于平直部分1−2和1−2处的挠度，其最大挠度为1.7 mm，仅为筛面中点最大挠度的4.37%，而远离弯折部位的区域1−2处的挠度与平直部分1−2的挠度相近，两者最大差值为2.37 mm。由此可见，筛面各部分挠度差异导致的相对错动是弯折部位产生内应力的重要因素。

2.2 筛面应力分析

基于2.1节中的有限元计算结果，绘制最大应力状态下筛面的剪切应力分布云图，如图7所示。从图7可以看出：筛面弯折区域属于高剪切应力分布区，最大剪切应力为202.65 kPa，远高于平直段部分的剪切应力，同时筛孔边缘等效应力较大，存在应力集中现象，这也与筛面现场实际破坏情况一致，说明有限元应力分析结果较可信。

图5 筛面的路径映射位置示意图

1—A1−A2；2—B1−B2；3—C1−C2。

图7 筛面剪切应力分布云图

由于高剪切应力区域主要位于弯折区域的中心部位，为更全面地描述筛面总体的应力分布，同样利用单元路径映射，绘制1−2，1−2，1−2这3处的最大等效应力−位置曲线，如图8所示。从图8可以看出：由于筛面几何结构和边界条件的对称性，沿筛面宽度方向，各处等效应力曲线均关于筛面几何中线呈对称分布；应力幅值均呈现先增大后减小的趋势，1−2和1−2这2处的等效应力曲线均存在较大幅度的局部波动，这主要是由于筛孔的存在使得筛面局部刚度呈现不连续性，而1−2处于盲板处，因而应力幅值变化较小。在筛面中部，弯折区域的1−2应力水平比其他部分的高，因而更易产生裂纹并扩展到其他位置。图9所示为实际生产中筛面破坏位置。由图9可知：模拟结果与筛面实际位置相吻合，可见模拟结果具有较高的可信性。

1—B1−B2；2—A1−A2；3—C1−C2。

图9 筛面实际破坏位置

3 响应面模型的建立

为进一步降低聚氨酯筛面工作应力，延长其使用寿命，现利用Creo与ANSYS Workbench联合仿真的方法对筛面弯曲半径和弯折角度进行优化。由于筛面变形呈现非线性特点，单纯循环利用有限元软件寻优计算耗时长，且具有不确定性，因此选择基于“试验设计−代理模型−全局优化”的混合优化策略搜索最优解，即通过试验设计(DOE, design of experiment)方法进行合理抽样，用最少的设计点尽可能全面地反映模型特征；运用近似模型方法，建立设计变量与响应变量之间的数学表达式；最后利用自适应模拟退火、遗传算法、Pointer 算法等全局优化算法在近似模型上进行全局优化。优化流程如图10所示。

图10 优化流程

3.1 响应面法和子模型法

响应面法(RSM, response surface methodology)是常用的近似模型方法，其计算精度与高精度模型相近，但计算量小、计算周期短，且能够过滤数值计算噪音，易于寻优，适宜于结构的非线性设计[18−19]。

选取筛面安装时的弯折半径和弯折角度为设计变量，并表示为矩阵形式[1，2]T，以筛面最大剪切应力1(1，2)和最大等效应力2(1，2)为优化目标。

由于高应力区主要分布在筛面弯折区域，为降低有限元模型计算量，减少计算时间，本文在AWB(ANSYS workbench)计算流程的基础上，采用子模型分析方法[20−22]，即在整体模型的基础上，通过边界条件传递，仅选取弯折部分作为子模型，进行细化计算。通过模型缩减，筛面子模型经过细化后划分网格69 906个，节点128 549个，分别较原模型降低51.8%和51.36%，网格畸变度由0.39降低至0.23，可见子模型方法在提高网格质量的同时减少了有限元分析计 算量。

3.2 试验设计流程

考虑到试验精度和计算成本，本文选择适用于二次多项式响应面模型采样的中心点复合设计(central composite design, CCD)方式[23−24]进行试验设计，弯曲半径1取值范围为20 mm≤1≤40 mm，弯曲角度2取值范围为90°≤2≤150°，总试验点数可以表示为

=0+2y+2y(6)

式中：0为中心点重复次数，本文取0=3；y为试验因素数，y=2。

通过试验设计，共生成11组设计参数，根据生成的设计参数，利用AWB 软件DX模块调用Creo软件，重构筛面模型，并按照设定的分析流程自动进行有限元分析，得到各组设计点所对应的最大等效应力1和最大剪切应力2，结果如表1所示。

根据获得的试验点数据，利用全二次多项式法标准响应面(standard response surface-full 2-nd order polynomials)生成1(1，2)和2(1，2)关于弯折半径1和弯折角度2的响应面，分别如图11~12所示。

3.3 响应面模型检验与分析

得到响应面近似模型后，为了保证拟合模型的准确性，需要对模型进行精度检验，为此利用方差检验分析(ANOVA)[25]检验方程显著性，结果如表2所示。

表1 不同设计参数所得结果

(a) 设计点−最大剪切应力三维趋势图；(b) 设计点−最大剪切应力等值线图

(a) 设计点−最大等效应力三维趋势图；(b) 设计点−最大等效应力等值线图

表2 方差检验分析结果

由表2可知：最大剪切应力响应面模型1的大于其检验临界值(显著性水平为0.05)，显著性检验指标＜0.05；最大等效应力响应面模型2的大于其检验临界值(显著性水平为0.01)，显著性检验指标＜0.01，2组响应面模型的不可靠概率分别小于5%和1%，说明其与真实有限元计算模型的逼近程度高，能够较好地满足预测精度要求。不同模型的残差正态分布概率如图13所示。由图13可知：试验值的残差正态概率分布均位于直线附近，说明响应面模型能够较好地预测试验结果。

为了得到适应于实际工程的优化结果，需要通过响应分析来判断设计变量的改变所引起的结构响应变化趋势，以便对选取的优化结果进行修正。以设计点 (25 mm，120°)为例，基于所建立的响应面模型可以绘制出局部变化曲线，如图14所示。从图14可以看出：当弯折安装半径1一定时，随着弯折角度2增大，聚氨酯筛面最大等效应力降低而最大剪切应力先增大后减小；反之，当弯折角度2固定，随着弯折半径1增大，最大等效应力和最大剪切应力均先增大后减小。

(a) 模型1残差正态概率分布；(b) 模型2残差正态概率分布

(a) 最大等效应力随弯折半径的变化；(b) 最大等效应力随弯折角度的变化； (c) 最大剪切应力随弯折半径的变化；(d) 最大剪切应力随弯折角度的变化

4 遗传算法优化

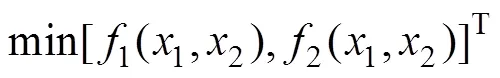
基于多目标规划方法[26−28]，定义最大剪切应力1(1，2)为优先优化目标，最大等效应力2(1，2)转化为约束，规定优化过程中2(1，2)不大于初始值。NSGA-Ⅱ遗传算法的参数设置如表3所示。同时为获得较优的初始种群，利用转移哈默斯利抽样技术(SHSM，shifted hammersley sampling method)，抽取均匀分布于设计空间中的样本点，并对其进行权衡排序，以避免算法过早收敛。优化过程中设计点−优化目标迭代曲线如图15所示。由图15可知：初始状态下1(1，2)和2(1，2)均出现较大幅度振荡，随着迭代次数增加，最终1(1，2)和2(1，2)迭代曲线趋于稳定。应力优化前后对比如表4所示。

(a) 最大剪切应力迭代曲线；(b) 最大等效应力迭代曲线

表3 NSGA-Ⅱ遗传算法参数设置

表4 应力优化前后对比

由表4可以看出：优化后筛面弯折区域剪切应力较优化前降低12.6%，优化效果明显。筛孔边缘最大等效应力比优化前的略有减小，满足设计要求。

为了验证响应面模型优化结果的正确性，将优化后的设计变量的最终取值代入有限元模型，计算得到筛面剪切应力云图，如图16所示。由图16可知：筛面最大剪切应力为179.28 kPa，而表4中响应面法应力优化结果为177.18 kPa，二者相对误差仅为1.17%，可见响应面优化结果是可信的。优化后的筛面平直段最大挠度为38.211 mm，相较于优化前的38.824 mm仅降低1.58%，对筛面筛分能力基本无影响。

图16 优化后的筛面剪切应力分布

5 结论

1) 建立实际安装状态下的弛张筛筛面参数化模型，基于有限元数值模拟，获得筛面整体的运动学响应；通过与理论计算结果进行对比，验证了有限元分析流程的正确性。

2) 沿宽度方向，筛面各处等效应力呈先增大后减小的趋势，其中筛面弯折区域属于高剪切应力分布区，与实际破坏位置情况相吻合；筛孔的存在导致应力幅值出现波动，其边缘存在应力集中现象。

3) 构建筛面优化的响应面模型，并获得了筛面安装最优几何参数；优化后，筛面最大剪切应力降低了12.6%，筛面的抗剪切破损能力提高。

[1] 程子曌. 我国煤炭洗选加工和煤质现状及“十三五”展望[J]. 煤炭加工与综合利用, 2017(5): 17−20. CHENG Zizhao. The present situation of coal washing processing and coal quality in China and the prospect of the thirteenth Five-Year Plan[J]. Coal Processing and Comprehensive Utilization, 2017(5): 17−20.

[2] DENG Xiaoyang. New progress of coal preparation technology in China[C]//XVIII International Coal Preparation Congress. Saint-Petersburg, Russia: Springer, 2016: 615−620.

[3] JIANG Haishen, ZHAO Yuemin, DUAN Chenlong, et al. Kinematics of variable-amplitude screen and analysis of particle behavior during the process of coal screening[J]. Powder Technology, 2017, 306: 88−95.

[4] ZHENG Gangfeng, ZHU Jinbo, XIA Wandong, et al. Banana flip-flow screen benefits coal preparation[J]. Filtration Separation, 2016, 53(4): 38−41.

[5] DONG Hailin, LIU Chusheng, ZHAO Yuemin, et al. Review of the development of dry coal preparation theory and equipment[J]. Advanced Materials Research, 2013, 619: 239−243.

[6] ZHANG Bo, ZHU Guangqing, LÜ Bo, et al. A novel and effective method for coal slime reduction of thermal coal processing[J]. Journal of Cleaner Production, 2018, 198(1): 19−23.

[7] 彭利平, 刘初升, 董海林, 等. 弛张筛面大挠度非线性变形分析与实验[J]. 煤炭学报, 2014, 39(5): 976−980. PENG Liping, LIU Chusheng, DONG Hailin, et al. Flip-flow screen deformation analysis and experimental surface nonlinear large deflection[J]. Journal of China Coal Society, 2014, 39(5): 976−980.

[8] 翟宏新, 杨丽, 李君. 工业型弛张筛系统参数的整体优化[J]. 煤炭学报, 2004, 29(1): 105−108. ZHAI Hongxin, YANG Li, LI Jun. Optimization of the whole system parameters of flip-flow screen[J]. Journal of China Coal Society, 2004, 29(1): 105−108.

[9] ZHAI Hongxin. Integral optimization of systematic parameters of flip-flow screens[J]. International Journal of Mining Science and Technology, 2004, 14(1): 77−81.

[10] 董海林, 夏云飞, 刘初升. 弛张筛支撑横梁结构改进对筛面可靠性影响的研究[J]. 矿山机械, 2012, 40(2): 72−75. DONG Hailin, XIA Yunfei, LIU Chusheng. Study on impact of structural reconstruction of support beam in flip-flow screen on reliability of screen surface[J]. Mining Processing Equipment, 2012, 40(2): 72−75.

[11] 王新文, 桑冬一, 赵军生, 等. 弛张筛筛面安装方式对其寿命影响的分析研究[J]. 煤矿机械, 2015, 36(7): 237−239. WANG Xinwen, SANG Dongyi, ZHAO Junsheng, et al. Analysis and research on effect of flip-flow screen surface installation to life[J]. Coal Mine Machinery, 2015, 36(7): 237−239.

[12] MEINEL A. Fine and very fine screening[J]. Mineral Processing, 2010, 51(1): 2−8.

[13] 韩清凯, 于涛, 孙伟. 机械振动系统的现代动态设计与分析[M]. 北京: 科学出版社, 2010: 76−78. HAN Qingkai, YU Tao, SUN Wei. Modern dynamic design and analysis of mechanical vibration system[M]. Beijing: Science Press, 2010: 76−78.

[14] 赵跃民, 刘初升. 干法筛分理论及应用[M]. 北京:科学出版社, 1999: 128−129. ZHAO Yuemin, LIU Chusheng. Theory and application of dry sieving theory[M]. Beijing: Science Press, 1999: 128−129.

[15] 王新文, 桑冬一, 孙鑫磊, 等. 振动弛张筛筛板预装长度的分析研究[J]. 矿山机械, 2015, 43(5): 102−106. WANG Xinwen, SANG Dongyi, SUN Xinlei, et al. Analysis of vibration flip-flow screen plate with relaxation length[J]. Mining Processing Equipment, 2015, 43(5): 102−106.

[16] 武继达. 振动式弛张筛动力学特性及疲劳寿命分析[D]. 徐州: 中国矿业大学机电工程学院, 2016: 38−40. WU Jida. Dynamic characteristics and fatigue life analysis of vibrating flip-flow screen[D]. Xuzhou: China University of Mining and Technology. School of Mechanical and Electrical Engineering, 2016: 38−40.

[17] 邹梦麒, 刘初升, 武继达,等. 张紧量对单边驱动式弛张筛筛面动力学参数的影响[J]. 煤炭学报, 2018, 43(2):571−577. ZOU Mengqi, LIU Chusheng, WU Jida, et al. Influence of tensional amount on dynamic parameters of unilateral driven flip-flow screen surface[J]. Journal of China Coal Society, 2018, 43(2): 571−567.

[18] 李军超, 王宾, 周同贵, 等. 基于数值模拟和响应面法的级进模成形优化[J]. 中南大学学报(自然科学版), 2015, 46(1): 66−72. LI Junchao, WANG Bin, ZHOU Tonggui, et al. Optimization of progressive die forming based on numerical simulation and response surface methodology[J]. Journal of Central South University(Science and Technology), 2015, 46(1): 66−72.

[19] 吕辉, 于德介, 谢展, 等. 基于响应面法的汽车盘式制动器稳定性优化设计[J]. 机械工程学报, 2013, 49(9): 55−60. LÜ Hui, YU Dejie, XIE Zhan, et al. The response surface method of automotive disc brake stability optimization design based on[J]. Chinese Journal of Mechanical Engineering, 2013, 49(9): 55−60.

[20] 翁顺, 左越, 朱宏平, 等. 基于子结构的有限元模型修正方法[J]. 振动与冲击, 2017, 36(4): 99−104. WENG Shun, ZUO Yue, ZHU Hongping, et al. Finite element model updating method based on substructure[J]. Journal of Vibration and Shock, 2017, 36(4): 99−104.

[21] YOU Junfeng, ZHONG Yanyan. Application of sub-model method for missile structure analysis[J]. Journal of Solid Rocket Technology, 2014, 37(2): 253−257.

[22] 陈世鸣, 陆云, 周聪, 等. 正交异性钢桥面横向焊接接头的疲劳寿命估算[J]. 中南大学学报(自然科学版), 2015, 46(9): 3461−3467. CHEN Shiming, LU Yun, ZHOU Cong, et al. Fatigue life estimation of transverse welded joints of orthotropic steel bridges[J]. Journal of Central South University(Science and Technology), 2015, 46(9): 3461−3467.

[23] 熊俊涛, 乔志德, 韩忠华. 基于响应面法的跨声速机翼气动优化设计[J]. 航空学报, 2006, 27(3): 399−402. XIONG Juntao, QIAO Zhide, HAN Zhonghua. Optimum aerodynamic design of transonic wing based on response surface methodology [J]. Acta Aeronautica et Astronautica Sinica, 2006, 27(3): 399−402.

[24] 张伟杰, 陆秋海, 缑百勇, 等. 基于逆响应面法的有限元模型修正[J]. 噪声与振动控制, 2013, 33(6): 5−10. ZHANG Weijie, LU Qiuhai, GOU Baiyong, et al. An inverse response surface method for finite element model updating[J]. Noise and Vibration Control, 2013, 33(6): 5−10.

[25] 姚克恒, 刘世豪, 夏拥军, 等. 开沟机作业功耗的正交试验分析及其优化设计[J]. 排灌机械工程学报, 2011, 29(6): 529−535. YAO Keheng, LIU Shihao, XIA Yongjun, et al. Orthogonal experiment analysis and optimization design for operation power of ditcher[J]. Journal of Irrigation and Drainage Machinery Engineering, 2011, 29(6): 529−535.

[26] 姜衡, 管贻生, 邱志成, 等. 基于响应面法的立式加工中心动静态多目标优化[J]. 机械工程学报, 2011, 47(11): 125−133. JIANG Heng, GUAN Yisheng, QIU Zhicheng, et al. Dynamic and static multi-objective optimization of vertical machining centers based on response surface methodology[J]. Chinese Journal of Mechanical Engineering, 2011, 47(11): 125−133.

[27] 夏玉峰, 杨显红, 郑晓凯, 等. 基于响应面法的钩尾框渐进热弯曲工艺多目标优化[J].中南大学学报(自然科学版), 2014, 45(9): 2977−2984.

XIA Yufeng, YANG Xianhong, ZHENG Xiaokai, et al. Multi-object optimization of incremental hot bending process of hook tail frame based on RSM [J]. Journal of Central South University (Science and Technology), 2014, 45(9): 2977−2984.

[28] 黄冬明, 武殿梁, 范秀敏, 等. 圆锥破碎机的多目标规划设计[J]. 机械工程学报, 2007, 43(3): 204−211. HUANG Dongming, WU Dianliang, FAN Xiumin, et al. Design for multi-objective planning of cone crusher[J]. Chinese Journal of Mechanical Engineering, 2007, 43(3): 204−211.

Numerical simulation of dynamic characteristics and parameter optimization of flip-flow screen surface

WU Jida1, LIU Chusheng1, WANG Zhenqian1, JIANG Haishen2, ZOU Mengqi1, QIU Wenqiang1

(1. School of Mechatronic Engineering, China University of Mining and Technology, Xuzhou 221116, China; 2. School of Chemical Engineering and Technology, China University of Mining and Technology, Xuzhou 221116, China)

Aiming to solve the problem about the damage of the screen mat of flip-flow screen, finite element analysis model of screen surface was established with consideration of the assembly form and working conditions of the screen surface. The distributions of deformation and stress at different positions on the screen surface under working conditions were analyzed. By combining the response surface method with the optimization technique and taking the installation radius and bending angle as the design variables, the second-order response surface approximate model reflecting the installation parameters and the stress of the screen surface was established through the design of the central composite test. The influence rule of the design variables on working stress of screen mat was analyzed. The response surface approximation model was optimized by combining the objective programming optimization method and NSGA-Ⅱgenetic algorithm, and the optimal geometric installation parameter was obtained. The results show that the shearing stress of screen surface is mainly distributed in the center of bending area. Through optimization, the minimal shearing stress is obtained when bending radius is 22.5 mm and the bending angle is 150°, 12.6% lower than the initial value.

screen surface; numerical simulation; experiment design; response surface method; sub-model; parameter optimization

10.11817/j.issn.1672−7207.2019.02.009

TH122

A

1672−7207(2019)02−0311−10

2018−03−11；

2018−05−11

国家自然科学基金资助项目(51775544，U1508210)；江苏省自然科学基金资助项目(BK20180650)(Projects(51775544, U1508210) supported by the National Natural Science Foundation of China;Projects(BK20180650) supported by the Natural Science Foundation of Jiangsu Province)

刘初升，博士，教授，从事选煤机械设计及动态优化研究；E-mail：liuchusheng@126.com

(编辑 伍锦花)