基于弹性弦模型的弛张筛面运动规律研究

李进武，王新文，王政浩，陈 欢，王 喆，耿润辉

(中国矿业大学(北京) 化学与环境工程学院，北京 100083)

细粒粘湿物料的深度筛分是如今筛分行业的热点问题，而弛张筛是有效解决细粒粘湿物料堵孔问题的设备之一[1-3]。弛张筛面在主浮筛框横梁带动下作一张一弛的周期性挠曲运动并和物料接触作用，是物料实现松散—分层—分级的最直接原因。分析弛张筛面的振动规律，对于指导物料的高效筛分有着重要的意义。

现有对弛张筛面运动的研究方法包括几何模型、弹性杆件模型和弹性弦模型，几何模型主要有三段圆弧模型和悬链线模型，弹性杆件模型主要包括弹性压杆模型、弯曲梁模型和细长压杆模型。其中，刘初升、赵跃民等将弛张筛面等效为两端可以移动的弹性压杆，建立了筛面动力学模型，得到了筛面上任意一点的位移、速度和加速度的解析表达式[4-6]；彭利平等将弛张筛面等效为失稳状态下的细长压杆，推导了筛面变形量随筛面长度变化的表达式[7]；翟宏新等比较了三段圆弧、弹性压杆和弯曲梁三种模型，得出三种模型在描述筛面位移、速度、加速度上具有一致性的结论[8]；董海林采用ANSYS有限元分析软件对筛面进行非线性瞬态运动学分析，通过改变筛面宽度，分析了宽度对筛面运动学特性的影响，通过改变位移载荷，探究了张紧量对筛面运动学的影响[9]；宁小波将弛张筛筛面视为两端可以自由移动的简支梁，得到了筛面中点的位移、速度、加速度表达式，据此研究了不同转速下，筛面张紧量对筛面速度和加速度的影响[10]；熊晓燕、顾成祥等人认为香蕉型弛张筛筛面有一定的倾角，筛面两端不对称，已有的模型并不能很好的描述其运动学行为，采用悬链线模型来描述筛面的非线性变形，并由此计算了香蕉型筛面在竖直方向上的位移、速度、加速度[11，12]。陈宝兴等基于弦振动模型和哈密顿原理，建立了任意张紧量下筛面的振动方程，并分析了空载下筛面的纵向和横向运动[13]。

在实际生产中，弛张筛面的运动会受到物料的影响，因此分析重载下筛面的运动更有意义。本文将物料作用力简化为筛面上的恒定载荷，并利用弹性弦模型建立了重载下筛面的横向振动微分方程，通过仿真模拟和数值计算对比，验证了该模型的可行性和准确性。

1 物料对筛面的作用

在物料筛分过程中，物料和筛面直接接触，因此获得动能。反之，在接触过程中，物料也会给筛面一定的反作用力，所以在分析筛面运动时应当考虑到物料对筛面的作用。姜泽辉等发现[14，15]，颗粒群作用在振动平台上的力随着振动强度的增加会出现倍周期分叉，在时间历程上具有周期性。徐宁宁[16]等人通过数值模拟发现，在简谐激励下，颗粒群对给料机槽底的压力为周期信号。

本文通过EDEM离散元法探究物料群对振动床面的作用。设计一个简易的圆筒形振动台，如图1所示，振动台底面半径为200mm，材料设置为钢，在振动台内生成20mm直径的颗粒，总质量为5kg，材料设置为煤，其余参数设置见表1。给予振动台正弦位移，观察不同振动强度k下颗粒群对底面的压力。

振动强度分别为1.6和4.8时的压力时程时程曲线如图2所示。可以看出，在不同振动强度下，颗粒群对筛面的作用力以周期的非谐和形式呈现，这与文献[14，15]实验和文献[16]模拟结果保持一致。对于任意的非谐和周期力F(t)可以通过傅里叶级数展开：

(1)

图1 振动台

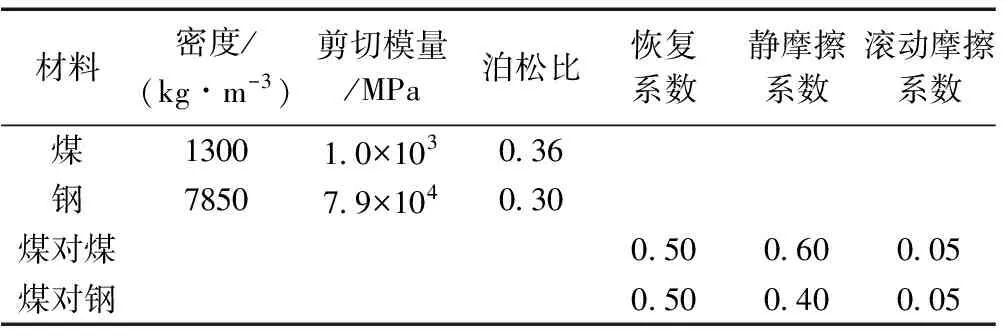
表1 EDEM中材料参数

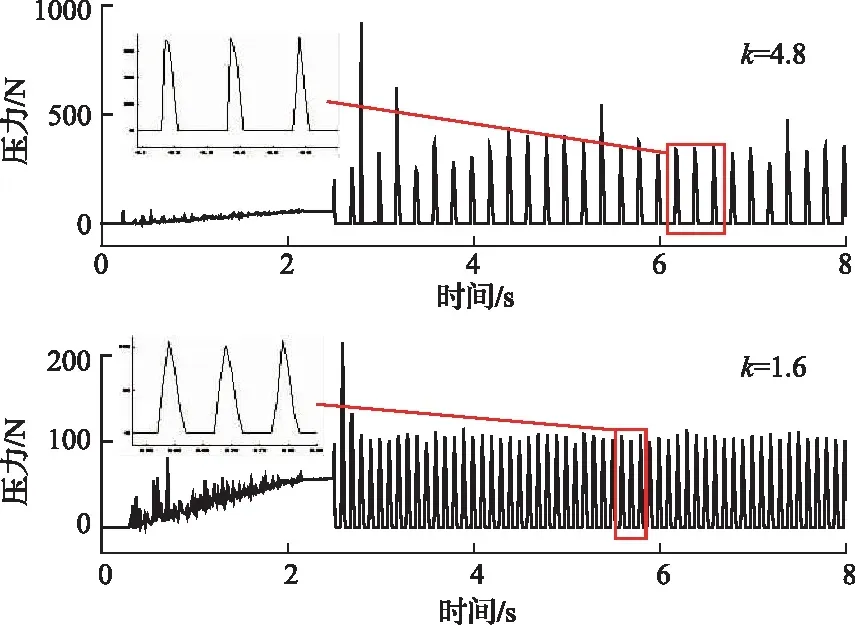
图2 不同振动强度下的压力时程时程曲线

将物料对筛面的反作用力按式(1)展开，如果只考虑常数部分，则可以认为常数部分为作用在筛面上的恒定载荷。在下文中模型分析时，理想的认为恒定载荷均布在筛面上，通过增大筛面密度的方式，将恒定载荷转换为筛面所受的重力来分析筛面运动。

2 弹性弦模型的建立

实际弛张筛面两端受正弦激励并具有一定倾角，现将其简化为两端在同一高度的水平筛面，且左端固定，右端作正弦运动：

U=Asinωt

(2)

式中，U为筛面右端位移；A为筛面右端位移激励幅值；ω为激励圆频率；t为时间。

忽略筛面运动在宽度方向的差异，建立图3所示的弹性弦模型。沿筛面长度方向建立X轴，垂直于筛面方向建立Z轴。初始时刻，筛面在物料压力及自身重力下处于静平衡状态。静平衡下的实际挠度曲线为悬链线，但当中点挠度与左右端点距离之比小于0.125时，抛物线和悬链线之间的差异很小。实际生产中，静平衡下的弛张筛面中点挠度与左右端点距离之比远小于此值。假设：筛面的静平衡挠度曲线为抛物线且静态张力沿X方向的分力处处相等[17]；筛面在运动过程不具有抗弯刚度，且拉伸过程中应力和应变服从胡克定律。

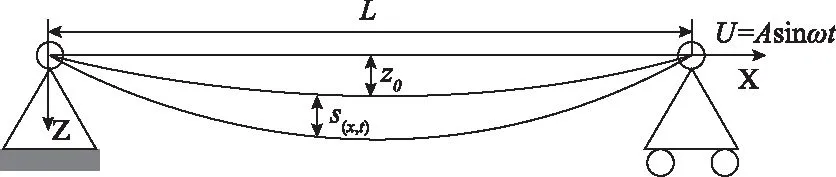
图3 筛面的弹性弦模型

对微元段进行受力分析，根据牛顿第二定律可得水平筛面横向振动微分方程[18]

(3)

其中，X方向静态张力：

(4)

X方向动态张力：

(5)

式中，m为线密度；w(x，t)为t时刻弦上x点处在Z方向上离静平衡位置的距离；c为粘性阻尼系数；z0为静平衡时筛面中点的挠度；L为筛面左右端点之间的距离；g为重力加速度；E为筛面弹性模量；B为筛面横截面积。

式(3)为二阶偏微分方程，可使用分离变量法求解，但其解析解较为复杂，本文使用龙格库塔法求解第一阶模态下振动的数值解。

3 模型的验证

有限元分析软件ABAQUS可以对柔性体非线性变形进行高精度仿真。弛张筛面材料为聚氨酯，属于超弹性材料，有限元软件通常采用Mooney-Rivlin模型描述这类材料的特性，网格单元一般选择杂交单元C3D8H[19]，本文中选用二参数Mooney-Rivlin模型。对于聚氨酯材料，Mooney-Rivlin模型中参数存在关系[20]。

C10=4C01

(6)

E=6(C10+C01)

(7)

D1=0

(8)

式中，C10、C01、D1为表征超弹性材料的材料常数。

现有研究方法大多先通过测量筛面硬度Hs，再根据经验公式确定弹性模量E，进而通过式(6)和式(7)确定Mooney-Rivlin模型中参数C10和C01的值。武继达[21]分别基于几种常用的经验公式的结果确定了参数的基本范围，然后通过仿真参数反演的方法确定了较为准确的经验公式：

(9)

本文利用式(9)计算参数C10和C01。使用邵氏硬度计对筛面进行硬度测试，实际测试所得筛面的硬度为87.9HA，代入公式可得弹性模量E=21MPa，C10=2.8MPa，C01=0.7MPa。D1取值为0，表示筛面为不可压缩材料[22]。在部件模块中建立筛面盲板，尺寸为325mm×500mm×4mm，如图4所示。两端距离为L=323mm，筛面自身质量0.741kg，均布于筛面的物料质量分别取3kg和4kg，并将作用在筛面上的均布载荷换算为筛面密度所受的重力，即筛面总密度=(物料质量+筛面质量)/筛面体积。于其他模块中赋予材料属性，划分网格，添加分析步。

图4 筛面三维模型

在筛长方向布置五个检测点，通过对比各个检测点的模拟和计算的位移时程曲线来验证模型的准确性。选择位移为输出变量，为保证计算速度，采样频率设置为100Hz。ABAQUS仿真过程只能对结点处的变量进行输出，故检测点必须布置在节点上，具体位置如图5所示。

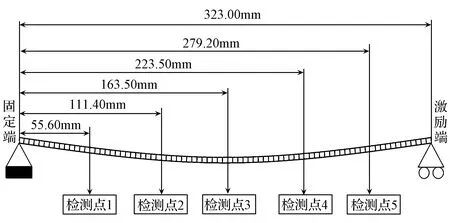
图5 检测点布置

载荷模块中将筛面一端固定，一端给予正弦位移激励，并添加重力加速度为9.81m/s2。模拟中未添加粘性阻尼，相对应的数值计算中取阻尼系数c=0，其他参数设置见表2。完成各参数设置后提交作业，从结果文件中输出各个检测点的位移，取振动稳定后十个周期内的模拟数据和数值计算结果对比，如图6所示。

表2 ABAQUS中参数设置

图6 位移时程曲线

图6(a)和图6(b)为物料质量分别为3kg和4kg时检测点3的位移时程曲线。检测点3距离固定端163.50mm，距筛面中点2.00mm，故检测点3可以近似视为筛面中点。由图6(a)可以看出，当物料质量为3kg时，模拟振动周期为0.10030s，计算振动周期为0.10031s，相对误差为0.001%；由图6(b)可以看出，加载物料质量为4kg时，模拟振动周期为0.09955s，计算振动周期为0.09940s，相对误差为0.2%。取十个周期的振幅，此处取振幅=(上振幅+下振幅)/2，对模拟和计算结果求平均值进行对比，数据见表3。由数据可以看出，加载物料质量为3kg时，模拟平均振幅为26.56mm，计算平均振幅为28.85mm，相对误差为7.9%；加载物料质量为4kg时模拟平均振幅为28.04mm，计算平均振幅为31.62mm，相对误差为12.8%。

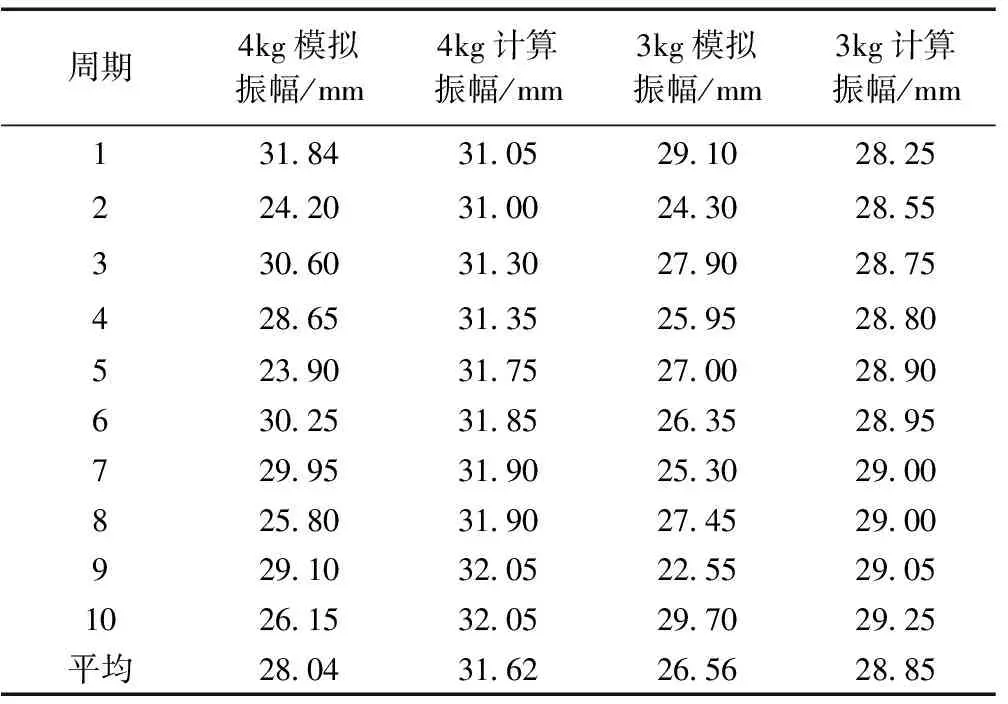
表3 十个周期内的振幅

图6(c)和图6(d)分别为物料质量为4kg时检测点2和检测点4的位移时程曲线。其中检测点2距离筛面中点50.10mm，检测点4距离筛面中点62.00mm，检测点2距筛面中点比检测点4更近。可以看出，检测点2振幅比检测点4大。故在以激励频率为主振动的筛面上，距离筛面中点越近，振幅越大，且筛面中点的振幅最大。

图6(e)和图6(f)为筛面物料质量为4kg时检测点1和检测点5的位移时程曲线。二者距离固定端的长度分别为55.60mm和297.20mm，离筛面中点的距离较远，振幅最大都不超过20.00mm。从图6(c)、图6(d)、图6(e)和图6(f)可以看到，检测点1、检测点2、检测点4、检测点5模拟所得的位移时程曲线并不平滑。对检测点1和检测点5的模拟位移进行功率谱分析，结果如图7所示。可以看出，检测点1和检测点5的位移不仅在基频10Hz处有峰值，在二倍频20Hz处也有一定的峰值。这说明筛面在以10Hz为主振动的同时，还叠加有更高频率的振动，所以之后可以考虑求解包含二阶或更高阶模态振型的振动方程用以更加精确的分析筛面的运动。另外从图6可以看出，各个检测点振动周期都约为0.1s，和激励周期一致。

图7 检测点1、5位移的功率谱密度

4 结 论

1)将重载下筛面的静平衡挠度曲线简化为抛物线，建立了一端固定，一端受轴向正弦激励的水平弛张筛筛面的弹性弦模型，推导了考虑粘性阻尼的筛面横向振动微分方程。

2)在筛面上布置五个检测点，通过有限元软件ABAQUS模拟和计算数据对比，发现各个检测点模拟和计算的位移时程曲线之间相对误差较小；从筛面中点处的位移时程曲线来看，模拟和计算的振动周期相对误差不超过0.2%，平均横向振幅相对误差不超过12.8%，验证了模型的准确性。

3)对比不同垂度下的筛面振幅可知，在相同位移激励下，保留一定的筛面松弛度，可以增大筛面的振幅。同时发现，筛面在以激励频率为基频振动的同时，还叠加有二倍频的高频振动。