煤矿井田构造复杂程度定量评价研究

施龙青，赵 威，刘天浩，翟培合，王 钊，吕昌兴

(1.山东科技大学 地球科学与工程学院，山东 青岛 266590；2.陕西郭家河煤业有限责任公司，陕西 宝鸡 721505；3.新汶矿业集团有限责任公司 华丰煤矿，山东 泰安 272213)

华北型煤田是我国重要的产煤区。该区域范围内的地质构造复杂，断层构造极其发育。根据不完全统计，在开采华北型煤田过程中，74.7%以上的突水事故都与断裂构造密切相关[1]。断裂构造复杂程度可以反映某一区域被断层切割破坏的程度。因此合理地评价断裂构造复杂程度，对指导矿井安全生产具有一定的实际应用价值。

矿井构造复杂程度定量评价的核心在于评价指标和评价模型两个方面。目前，国内关于矿井构造复杂程度定量评价的研究已经取得了很多成果[2-7]。徐志斌等[8]使用分维对煤矿断层网络复杂程度进行定量评价。施龙青等[9]在断层强度指数的基础上，提出了断层影响因子的概念。陈善成等[10]采用灰色模糊综合评价方法对构造复杂程度进行了定量评价。舒建生等[11]采用灰色关联分析方法和等性块段综合指数评价方法，对矿井构造复杂程度进行了定量化综合评价和分类。上述方法有各自的优缺点，其缺点主要体现在指标权重的确定，影响了评价的准确性。针对该问题，笔者在GRD的基础上，提出了一种改进的堆栈算法(Stacking)进行指标加权计算。实现了评价指标值间的有机融合，有效地处理了各指标间的相互作用，从而提高了评价结果的稳定性和可靠性。笔者以霄云煤矿为实例，选取了4个评价指标，构建了矿井构造复杂程度定量评价模型，对霄云煤矿构造复杂块段进行了预测分区。研究表明，评价结果与矿井实际情况相吻合，具有较高的准确性，为矿井断层突水危险性预测提供理论依据。

1 研究区概况

研究区位于鲁西南济宁市金乡县东南苏鲁交界处霄云镇，井田内地势平坦，为黄淮冲积平原。井田含煤地层为二叠系下统山西组及石炭系上统太原组。煤系上覆地层为古生界二叠系石盒子组深灰色泥岩、灰色粉砂岩、细砂岩、中砂岩、粗砂岩、砂砾岩和第三系粉砂岩、砂岩、砾岩，以及新近系松散沉积物[12-15]。煤系基底为中、下奥陶统石灰岩，奥陶系灰岩裂隙岩溶均较发育。

煤田内部构造比较复杂，以断裂构造为主，并发育次一级波幅较小的波状褶皱，断裂构造的方向性明显，为北倾的单斜构造。井田内褶曲不发育，断层较发育，局部地段揭露岩浆岩侵入体，以断裂构造为主，且均为正断层[16](图1)。按断层走向大体可分为两组，即NEE向断层组和NE-NNE向断层组，NEE向断层组发育特征与本矿区大型断裂构造线方向一致，该组断层一般落差均大于10m，数量相对较少，其生成时期及成因特征应该与大型断层相同或相似，NE-NNE向断层组受较大断层影响，多数分布于大断层两侧，受大断层控制。由于形成时间的差异，研究区内主要大断层之间相互交错，小断层分布于大断层四周，使得地层破碎严重，情况复杂，断层之间的相互连通的可能性极大。井田构造类型为复杂类型[17]。

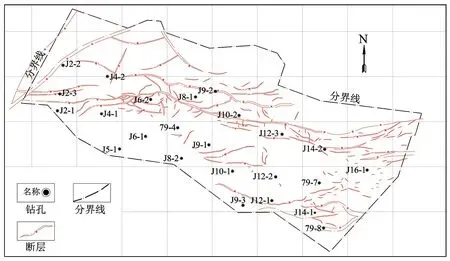
图1 霄云煤矿区域构造纲要图

2 构造复杂程度主控因素分析

研究区内主要构造为断层，本文在分析井田地质、构造、水文地质资料的基础上，确定了对于研究区矿井构造复杂程度的定量评价主要考虑断层方面的影响，因此选取断层分维值(DS)、断层密度(M)、断层尖灭点及交点个数(DF)、断层强度(F)指数4个指标作为霄云矿井构造复杂程度的评价因素，建立矿井构造复杂程度评价模型。

2.1 断层分维值(DS)

断层分维值包含断层条数、延展长度和相互交叉关系等多方面的变化关系，可作为一个综合性指标，充分反映断裂构造的发育程度[18]。实际求测过程中，将研究区的构造单元依次按400m×400m、200m×200m、100×100m、50×50m划分为若干个小网格，分别统计每一个单元内含有断层迹线的网格数N(r)值。将其投放到lgN(r)-lgr坐标系中，即可求得断层分维值：

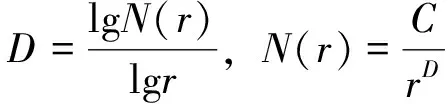
(1)

式中，D为断层分维值；N(r)为网格数目；r为网格边长；C为倍率。

求出各点断层分维值后，以协方差函数为依据，对研究区断层分维值进行随机空间建模的回归计算，得到霄云煤矿断层分维等值线，如图2(a)所示。

2.2 断层密度(M)

断层密度是研究地质构造复杂程度的定量评价的主要内容之一，断层密度是指单位面积或单位长度内具有断层的条数，它可以在某种程度上直观的反映一定范围内断层发育的数目，从而判断某区域内断层的复杂程度。在研究区内建立792个网格进行断层数目统计，然后对统计数据进行z-score标准化，确定数据波动范围后，得到霄云煤矿断层密度等值线，如图2(b)所示。

2.3 断层尖灭点及交点个数(DF)

采场顶板尖灭断层沟通采动裂隙，极易成为矿井突水的优势通道，且霄云煤矿小断层大部分分布在大断层附近，若断层相交，导水可能性会增加。因此，绘制200×200单元格，统计每个单元格内的断层交点和尖灭点个数，得到断层交点和尖灭点个数等值线，如图2(c)所示，用来预测矿井地质构造断层构造发育危险性。

2.4 断层强度指数(F)

由于自身性质的差异，不同断层对周边地层的影响能力及范围是不同的，单单断层密度仅能表示断层的数目，并不能全面评价不同区域构造复杂程度。故取区段面积内所有断层的延伸长度与其落差的乘积之和，作为断层强度指数来客观真实地反映断层落差、断层水平延展长度及断层数量的综合复杂程度。断层强度指数能定量评价断层的发育情况，可以客观反映该区域内的断层复杂程度，按式(2)计算。研究区断层强度等值线如图2(d)所示。

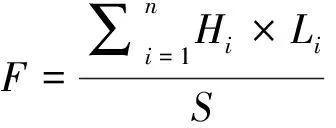
(2)

式中，F为断层强度指数；i为统计单元内断层的总条数；Hi为统计单元内第i条断层落差，m；Li为统计单元内第i条断层水平延展长度，m；S为统计单元面积，m2。

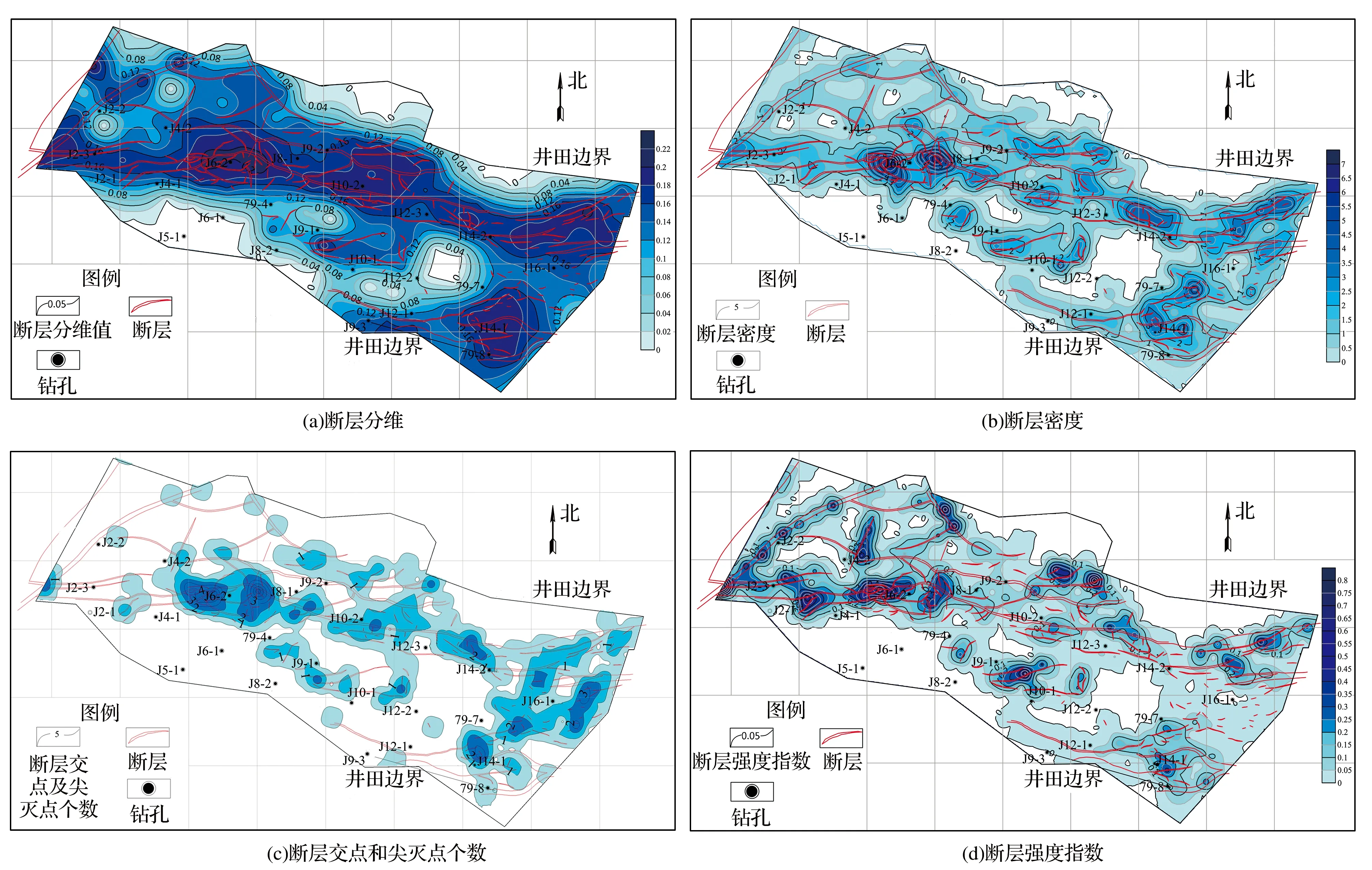
图2 断层影响因素等值线

3 构造复杂程度定量评价

3.1 基于非线性相关性的特征向量加权方法

构造复杂程度的评价本质上是对所有影响指标的耦合分析[19]。因此，指标权重的确定是解决多属性决策问题的关键。在四种影响指标中，都是根据研究区断层的不同性质所提出的评价方法，各个指标之间存在内在的联系与区别，通过指标间的相关性对不同指标进行分类评判是一种可以有效准确衡量各种因素对断层复杂性影响程度的评判方法。由于地质构造的复杂性和多样性，导致不同指标之间线性相关性普遍较差，因此采用灰色关联度(GRD)对指标间的相关性进行评价。

GRD源自灰色关联系数法(GRA)，是通过计算曲线间几何形状的差别程度[20，21]，从数据层面评价各指标之间的相关性，对数据间非线性相关极为敏感，但其缺点是无法结合所有指标和进行定量评价。

因此，在GRD的基础上，本文提出了一种改进的堆栈算法(Stacking)进行指标加权计算。Stacking算法是典型机器学习算法的一种，其基本原理为训练一个拟合模型用于组合其他各个拟合模型。本文通过GRA模型计算数据之间的非线性相关性，评价指标的重要性，并在此基础上建立了二级评价矩阵，进行矩阵特征向量转换，以此为依据建立评价模型。算法的详细步骤如下：

1)确定评价对象和评价标准。评价数据间相关性，首先确定反映系统行为特征的数据序列(参考序列)，其次确定影响系统行为特征因素的数据序列(比较序列)。参考数列记为xj={xj(1)，xj(2)…xj(n)}，比较序列记为xi={xi(1)，xi(2)…xi(n)}。

2)建立评价对象比较矩阵。在评价系统中，各因素列中数据的量纲不一定相同，若量纲不同时存在难以比较或比较差异过大的问题。为了保证结果的可靠性，在分析之前，需要对评价对象进行无量纲化处理，后建立评价对象判别矩阵。对比较序列xi={xi(1)，xi(2)…xi(n)}进行归一化变换：

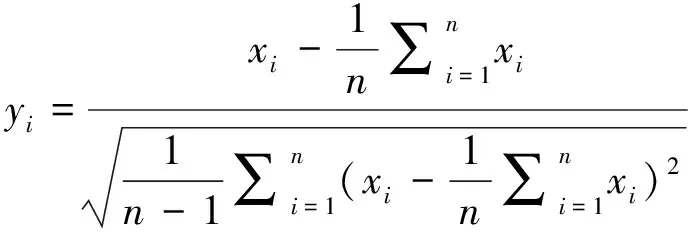
(3)

3)计算非线性关联度(灰色关联度)。灰色关联度指的是各评价对象分别与参考序列对应元素的关联系数的均值，以反映各评价对象与参考序列的关联关系：

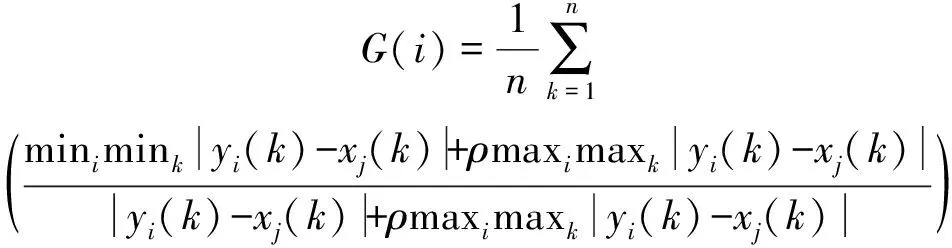
(4)

式中，G(i)为第i个评价对象对理想对象的灰色关联度；k=1，2，3，…，n；i=1，2，3，…，m；ρ为分辨系数，ρ∈(0，∞)，当ρ≤0.5463时，分辨力最好。一般取ρ=0.5。

通过GRD建立评价对象的关联度序列，并对关联度进行排序。GRD越大，相关性越好。其次，建立包含所有指标的评价矩阵。水平集的关联度aij与判断指数密切相关，由以下因素决定G(i)。

(5)

接下来，使用式(6)计算每个矩阵对应的特征向量如下：

i=1，2，…n；j=1，2，…m

(6)

其中，Wi是比较序列对参考序列的影响强度，是比较序列中因子的权重值。为了保证方程的有效性，对计算完成的矩阵进行了一致性测试，见式(7)。

CR=CI/RI

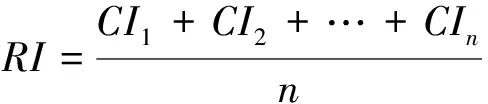
(7)

一致性试验是指确定判断矩阵A的允许范围。n×n一致性矩阵的唯一非零特征根是n。n×n正矩阵的最大特征根λ，大于或等于n，当且仅当λ=n，则矩阵A是一致的。当CR<0.1时，判断矩阵通过一致性检验，即权重分配合理。

3.2 指标权重的确定

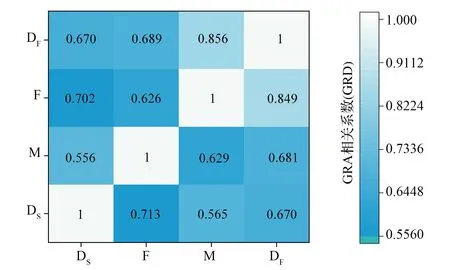
图3 影响因素关联系数热力图

考虑到DS、DF、M、F分别作为参考序列，每个指标的GCC是基于式(4)计算的。评价指标GRD的计算，每个指标的GCC以及比较序列和参考序列之间的关系如图3所示。由图3可知，G(DS)=0.649，G(DF)=0.738，G(M)=0.726，G(F)=0.622。

根据各指标GRD值的差异，建立了五级标度法见表1，基于表1建立了判断矩阵A，见表2。

基于式(6)，特征向量Wi计算结果为：WDS=0.1153，WM=0.3293，WDF=0.4925，WF=0.0629。

根据式(7)计算结果显示，最大特征根为4.1701，根据RI表查到对应的RI值为0.89，因此CR=CI/RI=0.0637<0.1，通过一次性检验。所以权重系数有效，判断矩阵A的一致性是合理的。

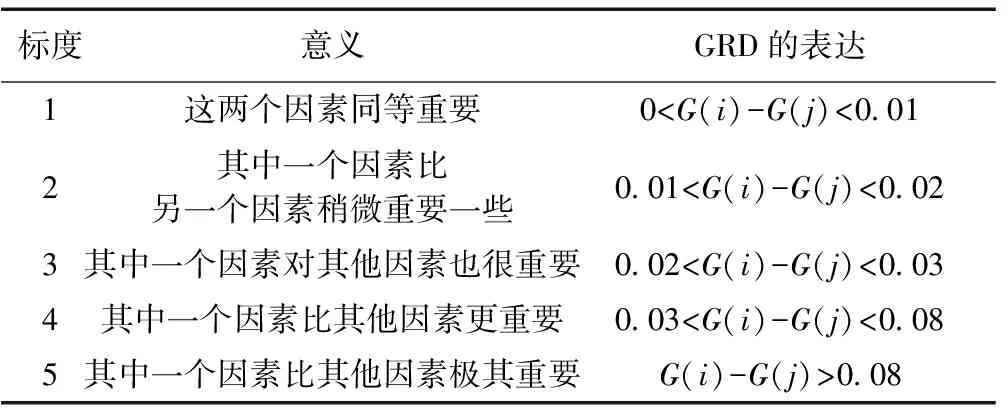
表1 利用GRD改进的五级标度法

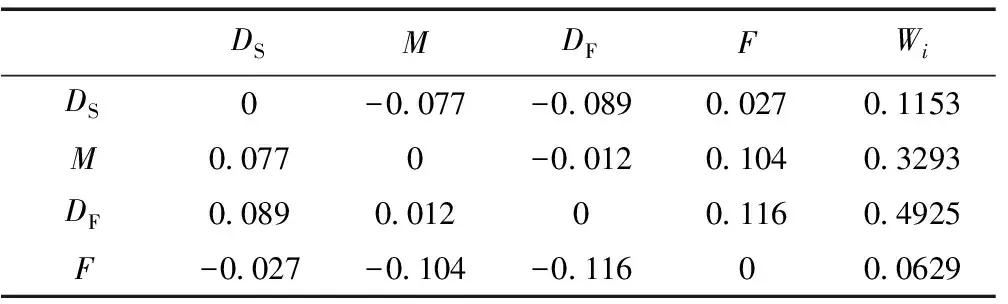
表2 判断矩阵A

3.3 矿井构造复杂程度定量评价

将各评价指标归一化后的数据导入ArcGIS中，建立断层分维值、断层密度、断层尖灭点及交点个数和断层强度指数的归一化专题图。再将权重值分别赋予4个评价指标，应用ArcGIS对各评价指标的归一化专题图进行融合计算，得到矿井构造复杂程度定量评价模型，即式(8)：

0.3293A2+0.4925A3+0.0629A4

(8)

式中，Qt为断层危险性指数；Aj为第j个评价指标的归一化值。

根据矿井构造复杂程度定量评价模型，通过对Qt进行统计分析，运用聚类分析的方法进行分级。聚类分析是一种基于中心的聚类算法(K均值聚类)，通过迭代，将样本分到K个类中，使得每个样本与其所属类的中心或均值的距离之和最小[22，23]。与分层聚类等按照字段进行聚类的算法不同的是，快速聚类分析是按照样本进行聚类。其分析步骤主要是根据字段进行因子差异性分析，见表3。其中定量数据采用方差分析，定性数据采用卡方检验，可基于显著性进行差异分析。

分析每个分析项是否小于0.05或者0.01(根据检验标准要求，严格的话使用0.01)若呈显著性，拒绝原假设，说明两组数据之间存在显著性差异，可以根据均值±标准差的方式对差异进行分析，反之则表明数据不呈现差异性。定量数据差异性的结果显示，基于Qt，显著性P值为0.0001，水平上呈现显著性，拒绝原假设，说明不同类别在Qt上存在显著性差异，可以根据均值±标准差的方式对差异进行分析。最终确定分级阈值分别为0.204、0.552。

表3 定量字段差异性分析

Qt的值和矿井构造复杂程度的关系，Qt越大，表明矿井构造复杂程度越大。以断层危险性指数为依据，根据阈值将研究区分为三种块段(表4)，并得到构造复杂块段分区图(图4)。其中岩层完整区为无构造发育块段，且该区域离断层较远，基本脱离断层影响范围，地层较完整；构造影响区为区域内存在少量断层或在断层影响范围内，地层收到构造影响，部分破碎，存在裂隙；构造破坏区为块段内存在大量断层，且断层相互交错，构造应力集中，地层破碎严重，存在大量裂隙，该块段内地层赋水能力强，且断层间连通性好，有着较好的水力联系。

表4 矿井构造复杂程度分级

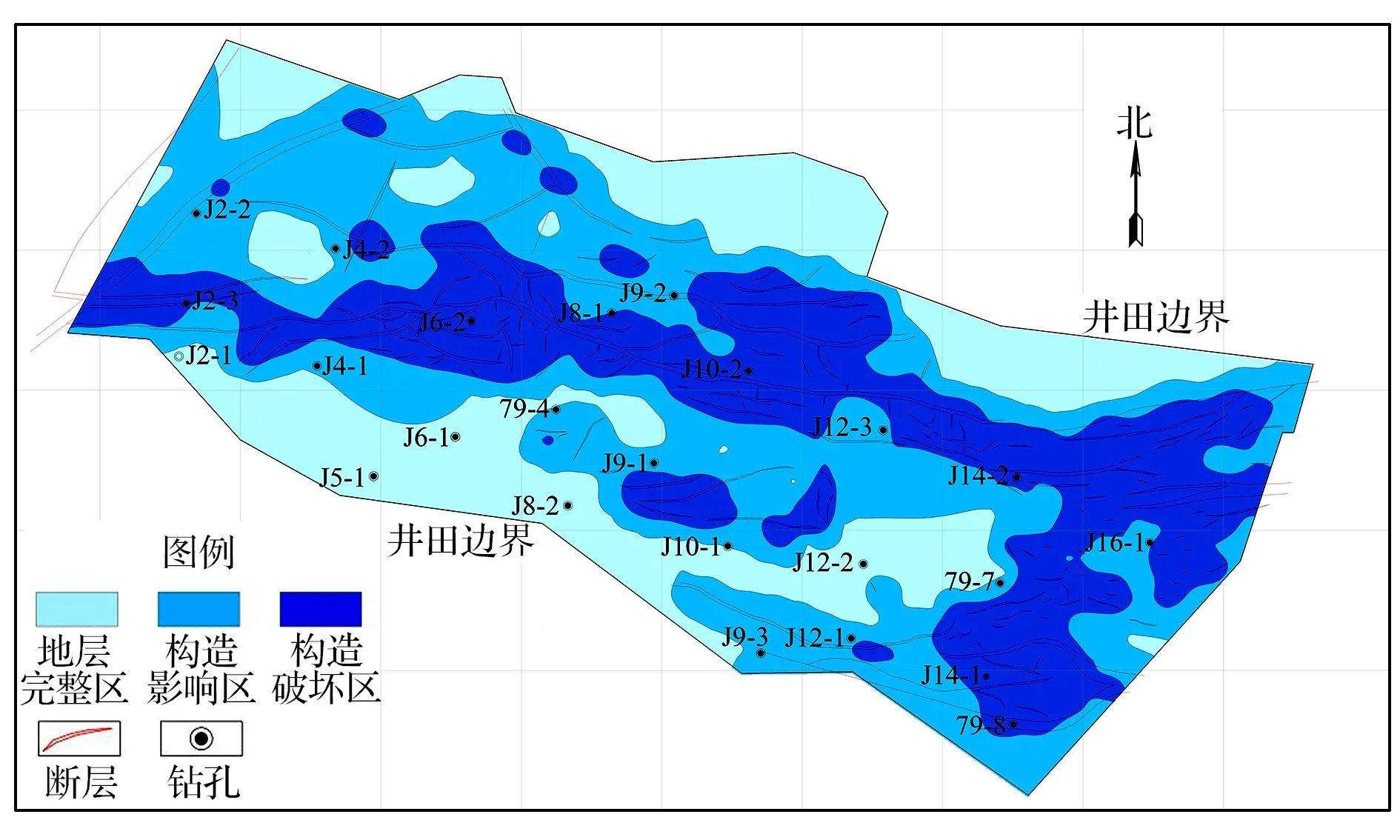
图4 构造复杂块段分区图

4 构造复杂程度评价模型验证

为了进一步判断构造复杂块段分区模型的正确性，在研究区构造复杂块段分区的基础上，每个分区所有钻孔的基岩岩心采取率进行统计分析。岩心采取率是指钻探过程中，取出的岩心长度与回次进尺的比值，能一定程度反映岩层的破碎程度[24]。岩心采取率公式为：

式中，c为岩心采取率；hi为该钻孔内累计取出岩心的长度，m；Hi为钻探过程中回次进尺的长度，m。

岩心采取率低，说明岩体破碎，岩体的裂隙发育好，透水和储水能力强，反之，则岩体完整，裂隙发育差，透水和储水能力弱。各区段岩心采取率如图5所示。

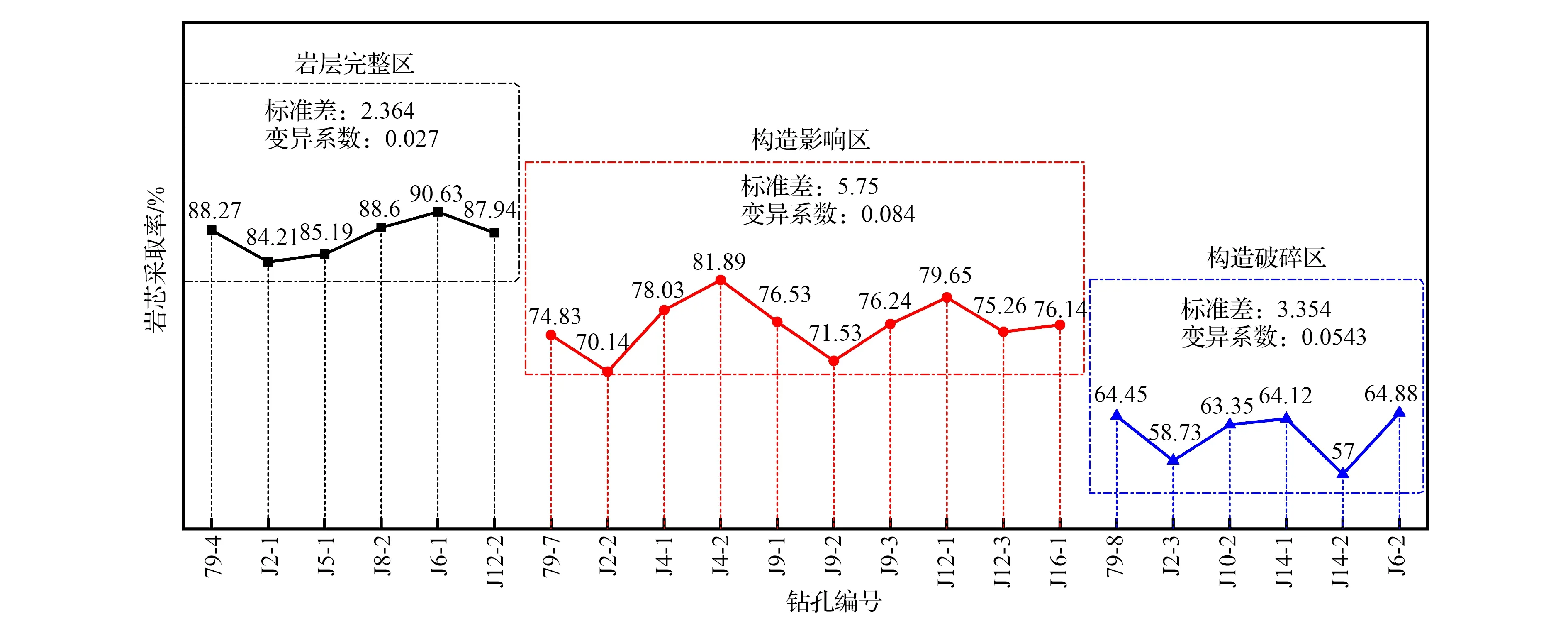
图5 各区段岩心采取率统计图

通过井田内岩心采取率统计表可以看出，岩层完整区内平均岩心采取率为87.47%，构造影响区内平均岩心采取率为76.02%，构造破坏区平均岩心采取率为62.09%，不同区段内岩心采取率有着明显阶梯状差异，说明以断层危险指数为依据的构造复杂性分区的差异性明显。

通过各区段岩心采取率统计图可以看出，岩层完整区岩心采取率最高为90.63%，最低为84.21%，标准差为2.364，变异性系数为0.027；构造影响区岩心采取率最高为81.89%，最低为70.14%，标准差为5.75，变异系数为0.084；构造破坏区岩心采取率最高为64.88%，最低为57%，标准差为3.354，变异系数为0.0543。各区段内岩心采取率具有相似性，较小的标准差和变异系数说明同一块段内岩心采取率差异性较小。不同块段间岩心采取率明显的差异性及同一块段内岩心采取率的相似性共同验证了以断层危险性指数为依据的构造复杂块段分区模型的正确性与适用性。

5 结 语

1)选取影响构造复杂程度的4个主控因素：断层分维值、断层强度指数、断层尖灭点及交点个数、断层密度，运用基于GRD提出的一种改进的堆栈算法(Stacking)来综合得出的矿井构造复杂程度主控因素的权重，建立了矿井构造复杂程度定量评价模型。

2)基于新的指标加权算法，来对整个研究区构造复杂程度进行定量评价，运用聚类分析方法进行矿井构造复杂程度分级，将井田范围内的复杂程度分为3个等级区域，包括岩层完整区、构造影响区、构造破坏区。

3)研究区构造破坏区主要集中在矿井中部和东部的区域，构造影响区主要集中在矿井中部；岩层完整区主要分布在矿井南部和北部区域。

4)根据岩心采取率结果，证实了研究区构造复杂程度分区的准确性。岩层完整区的岩心采取率为87.47%，构造影响区的岩心采取率为76.02%，构造破坏区的岩心采取率为62.09%。