矸石胶结充填二级搅拌机优化设计及仿真分析

王 壮，尉炳夫，刘锋珍

(1.山东科技大学 机械电子工程学院，山东 青岛 266590；2.绍兴市越城铸造有限公司，浙江 绍兴 312000；3.山东科技大学 资源学院，山东 泰安 271019)

矸石胶结充填采煤法是一种绿色开采方法[1，2]，采用矸石作为骨料，灰浆作为胶结料，在井下混合漫灌待充填巷道，凝固后支撑顶板，具有充填量大、充填体强度高等优点[3]。连采连充采煤技术是指在工作面上划分出若干支巷，通过连续采煤机或综掘机开采煤层，利用充填系统填充空巷，实现“采—运—充”一体化、采、充并行的现代化采煤技术[4]，具有长壁布局、短壁开采的特点[5]。

搅拌模块是充填系统的核心部分，搅拌机的性能直接影响着充填质量[6]。国内学者针对搅拌机的优化做了研究。刘柳[7]等人运用欧拉-欧拉模型和SSTk-ω湍流模型对搅拌机气液两相流进行数值模拟，得出了最优工况，缩短了混匀时间。曹小爽[8]等人使用Fluent软件对罐内流场进行仿真，通过安装带孔挡板帮助消除搅拌机的漩涡现象。高威[9]等人运用计算流体力学方法，考察了搅拌速率、液体粘度等对搅拌机内气液两相流流场的影响。许雯婧[10]等人通过采用锚框式桨叶结合三层四折叶涡轮桨的优化组合，改善了搅拌机循环流场。周勇军[11]等人发现安装角度为90°时，斜叶桨对轴向流的促进作用最明显，搅拌效果最好。刘钟鸣[12]通过改变搅拌转速、桨叶层间距、搅拌器离底高度等参数完成了固定床框式搅拌机的优化设计。王自强[13]设计了一种双吸涡轮桨式搅拌机，并对搅拌器、支腿的结构进行改进，在流体均匀性与功耗方面有所提升。歹晓晖[14]通过数值模拟得出了同倾角下斜叶圆盘涡轮式搅拌器比斜叶开启涡轮式搅拌器的能耗高的结论。以上研究针对的是流体的稳态分析，本文运用滑移网格法对搅拌机内固液两相流进行瞬态模拟，根据输出结果分析堵塞原因和叶轮参数对搅拌效果的影响。

1 工程概况

内蒙古长城六矿位于上海庙矿区，黄河河套鄂尔多斯盆地西北缘，处于内蒙古自治区西部与宁夏回族自治区接壤地带。矿井设计生产能力1.50 Mt/a，分别布置主立井、副立井和回风立井三个井筒，主、副立井分别负责煤炭运输和辅助运输，兼作进风井筒；回风立井负责矿井的回风。井田全区可采煤层共有6层，充填开采工作面布置在9煤，上距8煤层间距为18.11～22.06 m，煤层可采厚度1.22～4.65 m。顶板疏松为泥岩、炭质泥岩、粉砂岩、泥灰岩，底板为泥岩、炭质泥岩、粉砂岩、砂质泥岩。在采区集中上下山的一翼布置走向长壁工作面，由进风巷道、回风巷道、回风联巷形成整个工作面。工作面支巷设计坡度20°，支巷长度80 m，巷宽5 m。

连采连充矸石胶结充填系统主要由制浆系统与矸石制备系统两部分组成，制浆系统生产能力60 m3/h，矸石制备系统生产能力200 t/h。水泥、粉煤灰、水在一级搅拌机中混合，经高速搅拌后制成胶结料浆，流入二级低速搅拌机中暂存；地面矸石作为骨料[15]，经两级筛分、破碎后，在待充填巷道上端口进行淋浆后形成浓度为70%的矸石浆。矸石浆利用自重从待充填支巷上端口冲下，受到底端挡墙的阻挡后，进行自下而上的自流漫灌充填。当充填体临近上端口，使用喷射机进行上三角密实充填，实现100%接顶。充填系统的二级搅拌机采用型号为XT-600A的折叶桨式搅拌机，容量是一级搅拌机的数倍，用于提高成品灰浆向下输送的连续性，减少灰浆在管道和巷道中的离析沉降现象。

2 固液两相流密度分布特征

二级低速搅拌机结构如图1所示，其核心部件是折叶桨式叶轮，每层叶轮带有2枚叶片，相邻两层叶轮间垂直排列。罐体内径1.5 m，液面高度1.8 m，叶轮转速30 r/min，叶片倾角15°，叶轮直径1.1 m，叶轮层数4。

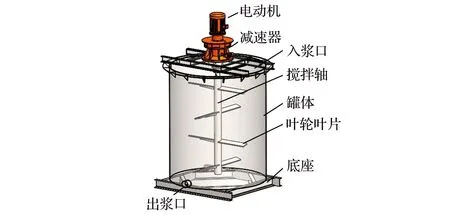
图1 二级低速搅拌机Fig.1 Two-stage low speed mixer

在现场应用中，二级搅拌机的出浆口多次发生堵塞，对矸石胶结充填系统的正常运行造成恶劣影响。灰浆可以视作固体粉料与水混合的固液两相流，在制定搅拌机优化方案前，需要分析流体的密度分布特征，以便确定优化指标。利用Fluent工具包，对二级搅拌机中的两相流密度场进行瞬态模拟。

2.1 系统前处理

根据搅拌机尺寸，创建叶轮、旋转流域、静止流域的搅拌模型，创建“流场域-旋转域”“旋转域-叶轮”两组减法布尔运算，保留流体部分。对流体域与旋转域布局多面体网格，统计共生成网格数量1688835。

湍流模型依旧采用可实现性k-ε模型，多相流模型选择Eulerian模型。多相流的主相为水，次相为固相，固相颗粒粒径100 μm，密度3000 kg/m3。旋转域旋转中心转速为30 r/min，在模型空间中添加重力加速度9.8 m/s2。将流体域外表面设置为固定的壁面，内表面设置为交接面；旋转域外表面设置为交接面，内表面即旋转轴设置为旋转的壁面，相对转速为0。

由于进入二级搅拌机的是由一级搅拌机制得的成品灰浆，假设0 s时二级搅拌机中的固液两相流是均匀的。设置固相的质量分数为0.25，由于罐体顶部非封闭设计，因此将表压设为0，主相与次相的初始速度设为0。选择分离式求解器，压力-速度耦合方案采用稳健性较好的SIMPLE方案，梯度插值方法选用更适合多面体网格的最小二乘法参与计算[16]，压力对流项的插值方法选用二阶迎风格式保证收敛精度。

2.2 结果分析

在瞬态求解器中将迭代步长设为0.05 s，迭代步数800步，仿真时长0～40 s，在后处理模块得到输出结果。罐内两相流在不同时刻的密度云图如图2所示，由图2可知，随搅拌时间增加，颗粒受重力影响逐层沉积，密度场产生明显的分层现象，罐顶与罐底间的密度差越来越大。因此，二级搅拌机的堵塞原因为罐内灰浆存在严重的固液分离，解决问题的关键是降低二级搅拌机的罐底密度。

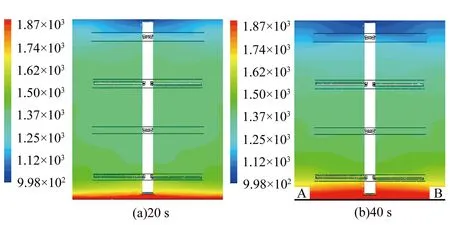
图2 二级搅拌机不同时刻密度分布(kg/m3)Fig.2 Density distribution in the two-stage mixer at different moments

以图2(b)为例，在罐底取一条穿过罐底中心的水平线段AB，A点坐标(-0.75，1.8，0)、B点坐标(0.75，1.8，0)。在该线段上取100个监测点，绘制不同时刻的罐底密度曲线如图3(a)所示。可以看出，二级搅拌机罐底密度曲线为单峰曲线，罐底中心处流体密度最高，显然，由叶轮离心力产生的主流对罐底中心影响小，不能产生足够的剪切力加速罐底中心的固相运动，导致固体粉料在罐底中心不断沉积。

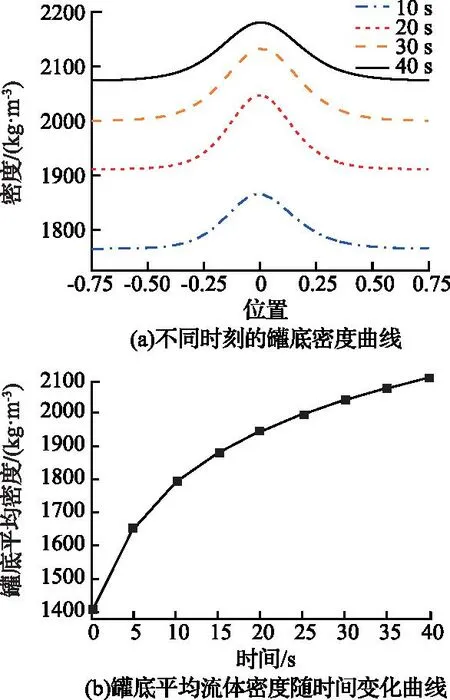
图3 罐底流体特性曲线Fig.3 Characteristic curve of the flow field

若通过所有监测点的密度平均值来表示罐底沉积程度，平均值越高则说明固相沉积越严重，出浆口堵塞风险越大。罐底平均流体密度计算公式为：

式中，X为罐底平均流体密度，kg/m3；ρi为第i个监测点的密度值，kg/m3；N为监测点总个数。

将密度平均值作为二级搅拌机的优化指标，得到指标随时间变化曲线如图3(b)所示，可以看出，随着搅拌的进行，罐底密度平均值逐渐增大，但增幅越来越小，流体密度逐渐趋向稳定状态。20 s时罐底平均流体密度已达到搅拌结束时的92%，为节省计算资源，将仿真时间统一设为20 s。

3 叶轮参数对搅拌效果的影响

影响搅拌性能的参数有转速、叶片倾角、叶轮直径、叶轮层数等[17，18]。本次优化的4组变量见表1，通过控制变量的方法，分别研究上述四个因素对搅拌效果的影响，观察罐底平均流体密度的改善效果以及搅拌轴功率的变化，最后根据四次横向对比结果选出合理取值范围。

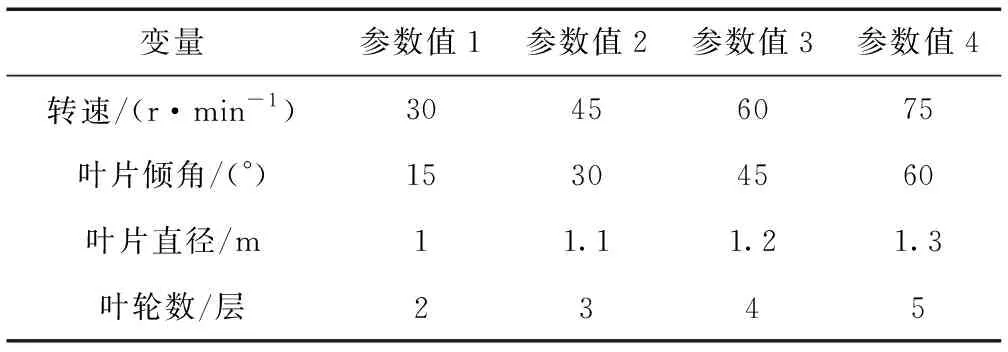
表1 二级搅拌机数值模拟参数Table 1 Numerical simulation parameters of the two-speed mixer

3.1 转速对搅拌效果的影响

折叶桨式叶轮通常用于低速工况[19]，图4(a)反映了不同转速下二级搅拌机的优化指标随时间变化情况，同时，根据仿真结果得到不同转速的搅拌轴功率如图4(b)所示。

图4 转速对搅拌效果的影响Fig.4 Influence of rotational speed on stirring effect

由图4(a)可知，不同转速下的罐底密度曲线具有以下特点：随时间增加，两相流在罐底的平均密度逐渐增大，斜率逐渐减小；高转速工况下能够更好的防止固相沉降，增大叶轮对流体的剪切力，因此随着搅拌的持续进行，各曲线在同一时刻的密度值差距逐渐增大；所有曲线在20 s时罐底的固相沉积量达到最大，转速每增加15 r/min，罐底平均流体密度降低约85 kg/m3。由图4(b)可知，转速与功率正相关，为保证搅拌效果，选择45～75 r/min作为二级搅拌机的转速取值范围。

3.2 叶片倾角对搅拌效果的影响

低速旋转的折叶桨式叶轮的直径一般占罐体内径的50%以上，直径过大会增加不必要的功耗，叶片倾角对搅拌效果和功率的影响曲线如图5所示。图5(a)中，15°、30°、45°、60°倾角下罐底平均流体密度分别为1944、1849、1821、1817 kg/m3，倾角为45°和60°时指标数据差距很小。图5(b)中，随倾角增大搅拌轴功率基本呈线性增加。

图5 叶片倾角对搅拌效果的影响Fig.5 Influence of blade inclination angle on stirring effect

分析可知，适当增大叶片倾角有助于降低罐底流体密度，考虑到功耗因素，因此确定15°～45°叶片倾角作为二级搅拌机优化方案的取值范围。

3.3 叶轮直径对搅拌效果的影响

改变叶轮直径后，罐底平均流体密度以及搅拌功率的变化情况如图6所示。

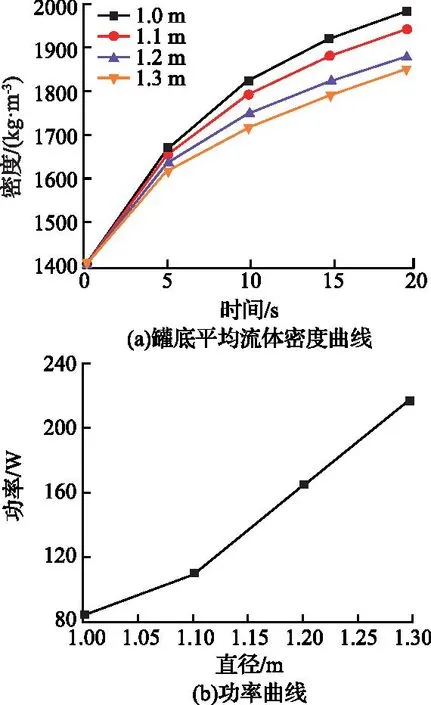
图6 叶轮直径对搅拌效果的影响Fig.6 Influence of impeller diameter on stirring effect

由图6(a)可知，增大直径有助于改善搅拌效果，当叶轮直径由1 m分别增大至1.2 m和1.3 m时，20 s时罐底平均流体密度分别降低了100 kg/m3和130 kg/m3。不同叶轮直径下搅拌轴的功率如图6(b)所示，叶轮直径与功率正相关，直径为1.3 m时的功率约是1.1 m时的2倍。

综合考察密度曲线和功率曲线可知，叶轮直径为1.2 m和1.3 m时罐底的两相流平均密度较小，搅拌效果好，选择1.1～1.3 m作为叶轮直径的优选取值范围。

3.4 叶轮数对搅拌效果的影响

折叶桨式叶轮一般有2～5层[20]，根据数值模拟结果，得到平均密度曲线和功率曲线如图7所示。

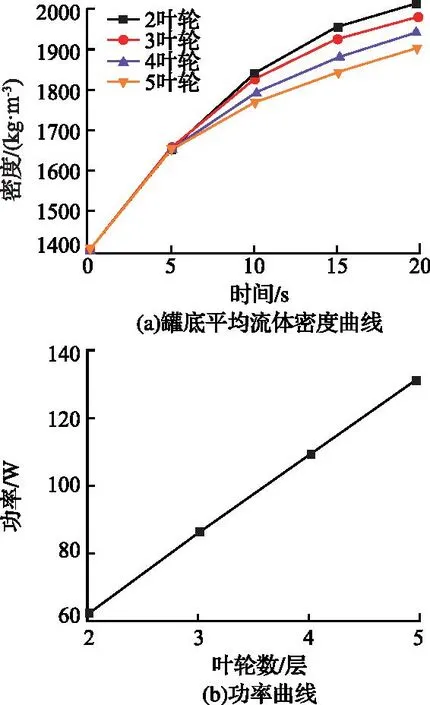
图7 叶轮数对搅拌效果的影响Fig.7 Influence of the number of impellers on mixing effect

从图7(a)中可以看出，叶轮增多后，同一时刻沉降至罐底的固体粉料数量下降，5层叶轮对罐底密度的改善效果最佳，20 s时5层叶轮下罐底密度平均值比2层叶轮低110 kg/m3。由图7(b)可知，叶轮数与功率间存在线性关系，叶轮数越多，功率越大。

通过以上分析可知，增多叶轮有助于降低罐底流体密度，改善搅拌效果，叶轮增多后搅拌轴功率会相应提高，但增幅较小，因此叶轮数为3～5层较好。根据前面所作的各变量参数改变时罐底平均流体密度变化曲线，进行优化指标对不同影响因素在单调区间内的灵敏度分析，计算公式如下：

式中，f1为某影响因素在单调区间内增加18%后的罐底平均流体密度；f0为各影响因素均为初始值时的罐底平均流体密度。

根据计算结果，得到各因素灵敏度数据依次为叶轮直径26%，转速10%，叶轮数8%，叶片倾角5%。

3.5 交互作用分析与参数优化

对各因素进行编码：转速为A、叶片倾角为B、叶轮直径为C、叶轮层数为D，根据前文确定的单因素取值范围，采用Box-Behnken设计方法进行四因素三水平响应面试验，研究各因素间的交互作用，设计最优方案，其中三水平分别为各取值范围的两端点值外加中间值。运用Design-Expert软件对试验结果进行分析，得到显著性统计表见表2。

表2 显著性统计表Table 2 Significance statistics

由表2可知，各项因素失拟项F值均大于0.05，表明模型具有较高的可靠性。单因素显著性顺序依次是A>B>C>D，多因素交互作用的显著性顺序依次是BD>BC>CD>AB>AD>AC，交互组的P值均大于0.05，说明各因素之间的交互作用不明显。

采用二次方程表示罐底平均流体密度与因素编码之间的关系：

X=1653.2-90.17A-68.25B-26.75C-14.17D-

7.5AB-4.25AC+4.75AD+16BC+32.75BD-

15CD+23.11A2+30.73B2+21.98C2-8.14D2

(3)

由输出结果得到，当转速为74.68，叶片倾角为34.03，叶轮直径为1.28，叶轮数为4.9时，X有最小数值解1543。通过取整得到优化方案：叶轮转速75 r/min，叶片倾角34°，叶轮直径1.3 m，叶轮数5。

3.6 结果验证

对最优组合进行仿真，与初始参数进行对比，优化结果见表3。

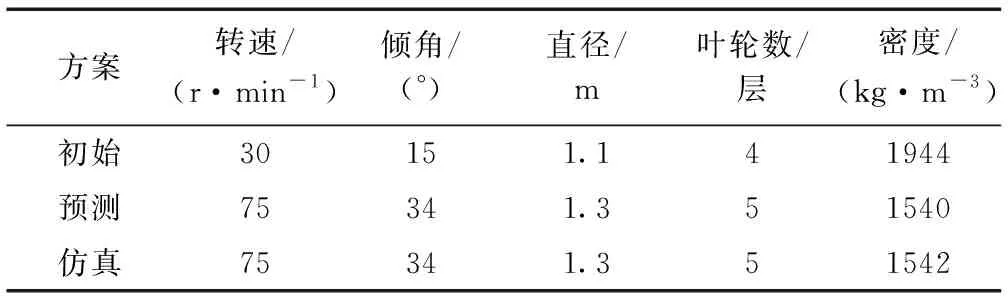
表3 优化结果对比Table 3 Comparison of the optimization results

从表3中可知，优化方案与初始数据相比，罐底流体密度得到了较大的改善，仿真结果与预测结果基本一致，证明了该预测模型的有效性。

对优化的二级搅拌机进行生产和试验，将灰浆浓度调整为20%，经过一个搅拌周期后，通过人工在二搅拌机底部出浆口处进行灰浆取样，使用量筒和密度计测量混匀后的灰浆样品的密度。经测得优化前的二级搅拌机的罐底密度为1985 kg/m3，优化后罐底1526 kg/m3，罐底密度降低23.1%。设备优化后罐底固相沉积问题得到了改善，灰浆流动性增强，达到了预期的优化效果，提高了充填系统的工作效率。

4 结 论

1)通过对二级搅拌机中的固液两相流进行瞬态模拟，得到了具有单峰曲线特征的罐底流体密度曲线，经分析后发现出浆口堵塞的原因为两相流存在严重的固液分离现象。

2)提高转速对于降低罐底处流体密度的作用效果最显著，转速越高，罐底密度越低，搅拌效果越好，但功率损耗增幅明显。

3)适当增大倾角可以减少罐底处的固相沉积，当叶片倾角从15°增大至45°时，罐底流体密度持续降低，继续增大叶片倾角至60°后密度变化较小。

4)增大叶轮直径和叶轮数有助于降低罐底处固液两相流的密度值，减轻固液分离程度，改善二级搅拌机的搅拌效果。