统筹·路径·阶梯：“倍的认识”单元教学设计与实践研究

浙江杭州市半山实验小学（310000） 虞欢欢

“倍的认识”是人教版教材三年级上册第五单元的内容，内涵丰富，是促进后续数学知识学习的重要基础。“倍的认识”也是学生对两个量关系认识从“相差关系”到“比率关系”的一次“质变”。

一、“倍”单元的教材研读及编排分析

（一）教材研读，倍的关联知识丰富

“倍”表示的是两数关系，而三年级上册“倍的认识”是比较两个数量关系的第四个阶段。此前其实也有涉及两个量关系的学习，但只局限于相差关系，教材从三年级“倍的认识”单元开始讨论两个量的“比率关系”。笔者对人教版教材两数关系的学习内容进行了整理。

两个数量的关系从“比多少”开始，到形成两个数量之间的特殊关系“倍”，再到五、六年级用“小数”“分数”“百分数”“比”来表示两个数量的倍比关系。整个概念体系的建构是按照“整数—分数—小数—比”的顺序依次进行的。

（二）编排分析，倍的课例安排不足

三年级上册“倍的认识”这一单元的编排顺序为引入概念、建立概念、应用概念。笔者通过实践发现本单元教材存在两个不足。

1.知识分散、重复、不全，不利于学生形成知识结构

知识单向重复多，不利于学生整体思考。“倍的认识”实质上就是对“倍数”“标准量”和“比较量”三者之间关系的认识，教材通过3 个例题，采用小步子渐进的教学安排。这样的教学会有明显的分散性和重复性，同时缺乏挑战性。

2.编排缺少后续关联，不利于学生形成知识结构

内容编排缺乏关联性，不利于学生形成知识结构。“倍”是数量之间的一种特殊关系，在学习“倍”之前我们已经在用“比多少”表示两个量之间的关系，后续还会学习“不到1 倍时用一个数是另一个数的几分之几或百分之几来表示”。教材编排中缺乏这样的知识关联，学生只是孤立地认识“倍”，不能很好地实现知识迁移，难以形成知识结构。

二、“倍”单元的学情调查及教学现状

（一）学情分析，收集学生学情

为了更好地进行单元教学，笔者在研究“倍的认识”前对学生进行了前测（略）并分析了结果。

1.学生对倍的理解，因相差关系产生一定的负迁移

前测第1 题中没有出现有关“倍”的字眼，学生习惯性用学过的“比多少”来描述两个量的关系，很少有学生用“倍”来描述两个数量之间的关系。笔者还发现，有些学生把3倍理解成了“相差3”，还有学生把3 倍理解成了“多3 倍”。对此，教师教学时要考虑“相差关系”的负迁移，引导学生从“相差关系”的概念中转变过来。

2.学生对倍有一定的认知基础，但缺乏本质理解

学生对“倍”的概念有丰富的生活经验和一定的认识基础，但缺乏本质的理解。前测中，有43.6%的学生画出的关系图中，苹果的数量是香蕉的3倍，但画的时候仍会把苹果放在香蕉的前面，这说明学生缺乏以香蕉为标准量的概念。另外，还有学生认为2 的1 倍是4，说明学生没有明白“比较量”的概念。这样的现象说明学生对“倍”的理解层次不一，对“标准量”“比较量”和“倍数”三者之间的关系是模糊的，没有真正明白倍数关系。

（二）教学分析，收集教学问题

除了学生对“倍的认识”这一学习内容存在一定困惑，教师在教学时也有许多的问题。教学中常见的问题收集如下。

1.概念教学集中于起始课，忽略概念的建构需要过程

学生一看到倍就用乘法，说明教师教学时并没有落实“对倍概念本质属性的认识”，其主要原因是教师在教学这个单元时只关注答题，忽视了对倍的理解。

2.学生的核心素养停留于关注，缺少素养提升的系统性规划

这个单元指向的核心素养主要是“几何直观”，具体表现在用图来表征倍的能力、用图来解决问题的能力和数形结合意识。在实际的教学中，教师对学生学习画图方法缺少进阶性指导，缺少由易到难的进阶规划，对学生几何直观的培养缺少系统性的规划。

三、倍的单元统筹教学实践及思考

（一）统筹安排：规划倍的课时结构及内容

1.整合与划分单元课时，统筹规划课时结构

基于以上整理和分析，笔者对“倍的认识”单元的课时结构进行了重新规划设计，规划后的课时安排如图1所示。

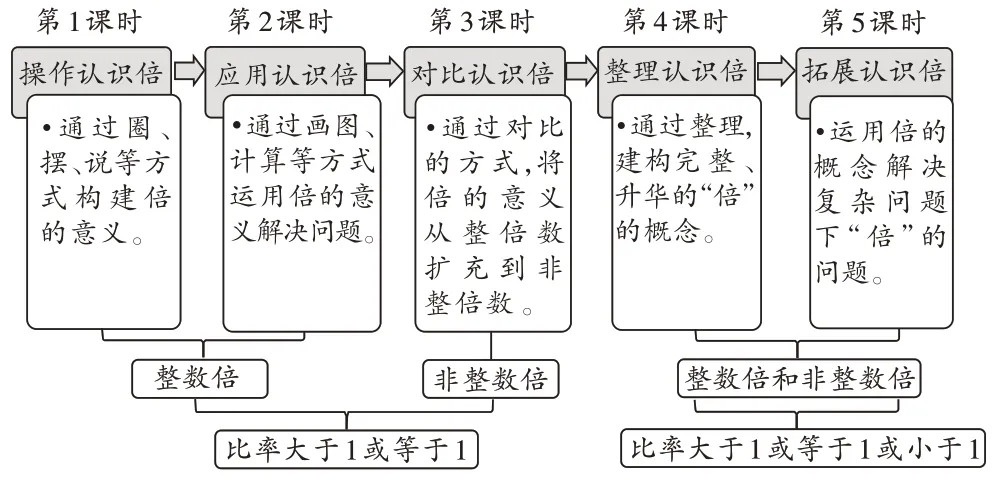
图1 “倍的认识”规划后的课时安排

本单元内容由原来的4 课时变为5 课时，分别是操作认识倍、应用认识倍、对比认识倍、整理认识倍、拓展认识倍。原来的课时安排缺乏结构性以及倍知识的完整性。而规划后的5 课时，先通过操作比较，把抽象的新知识“倍”与学生已经掌握的“几个几”建立联系，让学生初步认识倍的概念。再通过大量比较两个量的倍数关系，帮助学生建立倍的直观模型，使学生在解决问题的过程中表达出倍的本质特征，抽象概括出基本数量关系。最后，倍的复习和拓展促使学生整体地理解“标准量”“比较量”和“倍数”三者的关系，进而能够应用倍的意义去解决问题。教学内容涵盖了教材原来缺失的部分，并且建立了与后续知识的关联。

2.概念要素分解与重组，合理规划课时内容

倍的概念的内涵与外延非常丰富，这也是造成许多教师在教学中顾此失彼的原因。每个课时的教学内容要做合理的安排，避免有些课时内容过多、过难，有些课时过于简单。笔者认为概念要素的分解与重组是一个非常好的策略。

本单元内容分为四个一级要素，包括“倍的意义”“倍数”“标准量”“比较量”。这四个一级要素又可以分解成多个二级小要素（见表1）。

具体要素分布如图2所示。

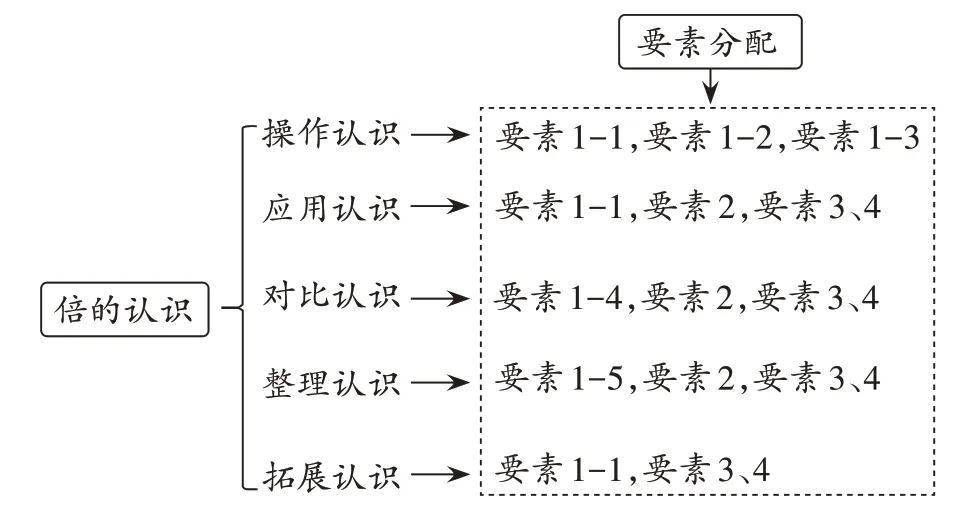
图2 “倍的认识”要素分布

合理分解要素是为了把大概念拆分成一个个小概念，然后合理地分配到每个课时中。这样一方面能使教师明确单元设计中要落实的具体内容，为后面课时做好铺垫，避免要素过多导致重复和遗漏；另一方面，有利于引导学生有梯度、有增量、有系统、有结构地进行学习。

（二）路径建构：厘清倍概念的建构路径

要想建构正确的概念，首先要让学生经历从“差比”到“率比”的讨论过程，从而规避知识的负迁移。

1.经历从“相差”到“比率”的辨析过程，消除知识经验的负迁移

在第1 课时的教学中，笔者用前测第1 题中四名学生的作品作为活动一的材料，其中三人的作品是相差关系，一人的作品是比率关系，也就是倍数关系（如图3）。

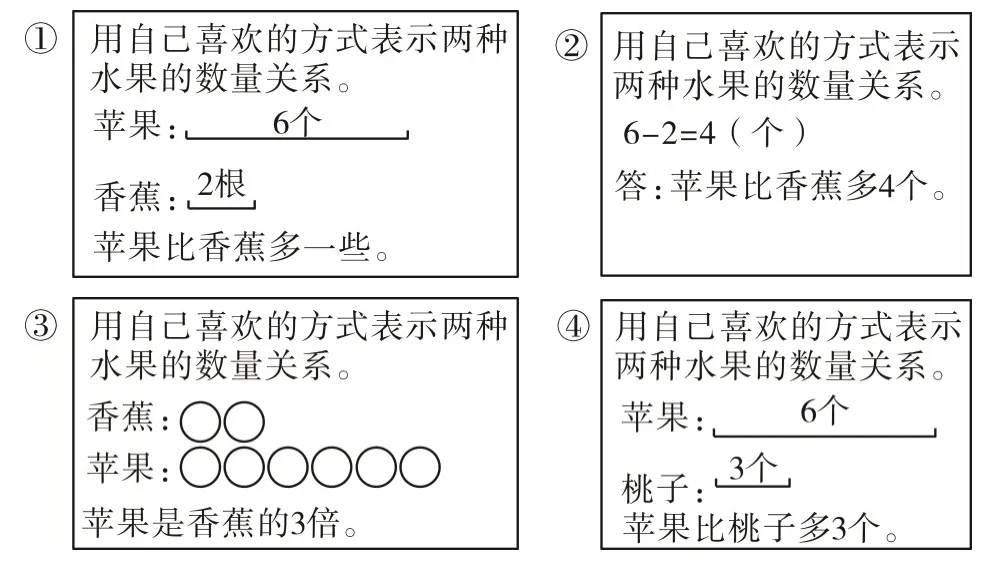
图3 第1课时活动一材料

笔者让学生用分类、对比的方式对这四幅图进行学习，感知“倍”也是两数关系的一种，且与比大小有所不同。

2.经历从“具象”到“抽象”的概括过程，剔除非本质因素的干扰

在第1 课时中，学生在认识到倍是一种新的两个数量之间关系后，聚焦图3 的第3 幅作品深入讨论“什么是倍？”。

在第1 课时活动二教学过程中，聚焦第3 幅作品，围绕为什么说“苹果是香蕉的3 倍”开展讨论。教师在此时为学生提供操作支架“圈一圈”，以及语言支架，即“香蕉有（）根，苹果有（）个（），所以（）的数量是（）的数量的（）倍”，帮助学生清晰、准确地建立“倍”的具象概念。

接着，笔者出示前测中学生的其他四幅作品（图略）。笔者先带领学生围绕“这些数量是不是3倍关系？”“怎么看出3 倍关系？”两个问题进行辨析、讨论、思考，重点引导学生用圈一圈的方式来清晰表达3 倍关系，接着让学生围绕“这四幅图都表示3 倍关系，它们有什么共同点？”进行讨论。通过隐去圈内的图形，启发学生逐步发现3 倍关系的特征（如图4）。

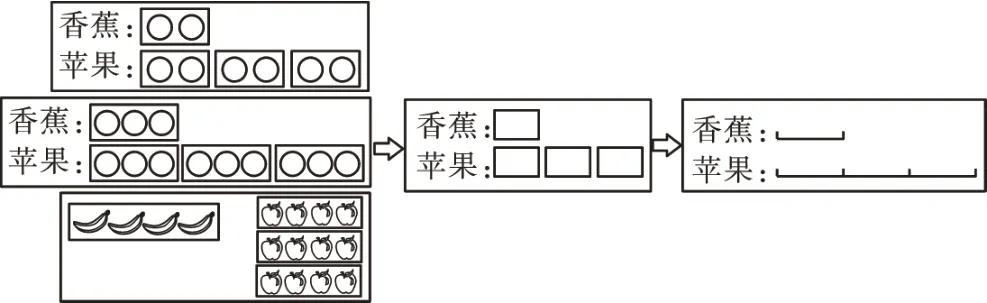
图4 3倍关系图

最后让学生重点围绕图3的第4幅作品进行讨论。这幅图中，香蕉和苹果可能有几个？通过讨论明确香蕉与苹果的个数有无数种可能，从而剔除非本质因素的干扰，逐渐将“倍”的具象概念过渡为“倍”的抽象概念。

3.经历从“认识”到“运用”的关系建构，认识倍中的三者关系

本单元第2 课时活动一和活动二的具体设计结构如图5所示。

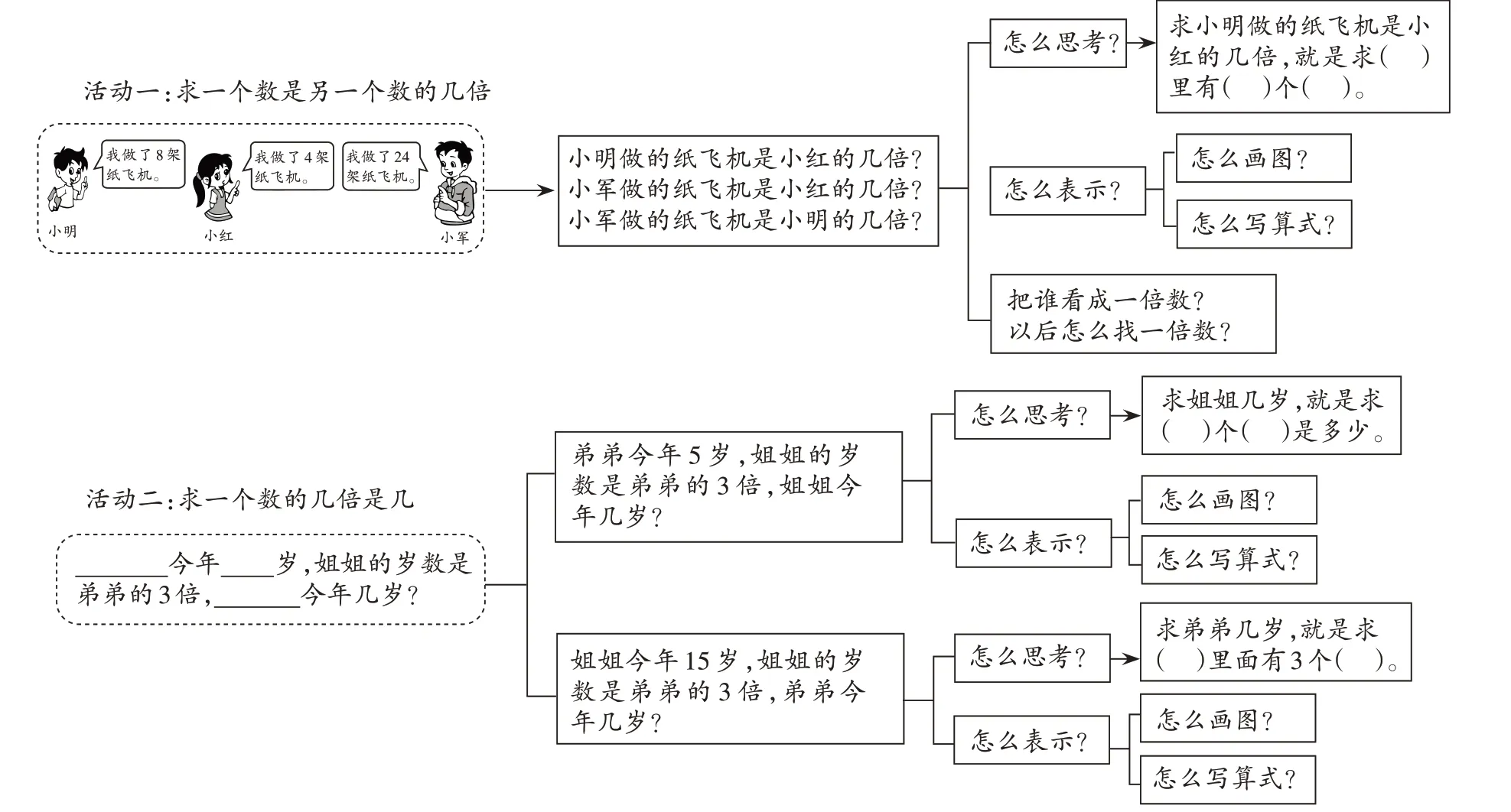
图5 第2课时活动设计

在第2 课时的活动一中，学生围绕同一题材，提出三个不同的求倍数问题，经历数量由少变多的过程，体验将数量图转化为线段图的过程，用语言、画图、算式表示求倍数就是“求比较量里面有多少个标准量”。横向对比三个问题的求解过程，总结比较量和标准量的关系。

活动二则通过改变已知条件，引出求比较量和求标准量的两种应用。其中，求比较量被作为重点内容进行探究，通过语言、画图、算式等方式体验求比较量就是求几个标准量是多少。在渗透求标准量的过程中，逐步完善“倍”的概念中三个数量之间的关系建构。

4.经历从“一般”到“特殊”的演变过程，了解倍的内涵与外延

第3 课时的安排是在整倍数应用的基础上，对“比较量的数量”进行调整。学生的学习顺序是从“香蕉是苹果的3 倍”到“香蕉比苹果的2 倍多4 个”或者“香蕉是苹果的3 倍少2 个”，即当数量不是整倍的时候，可以用几倍多几或者几倍少几来表示关系。这样，学生对“倍”的认识就有了新的突破。具体设计如图6所示。

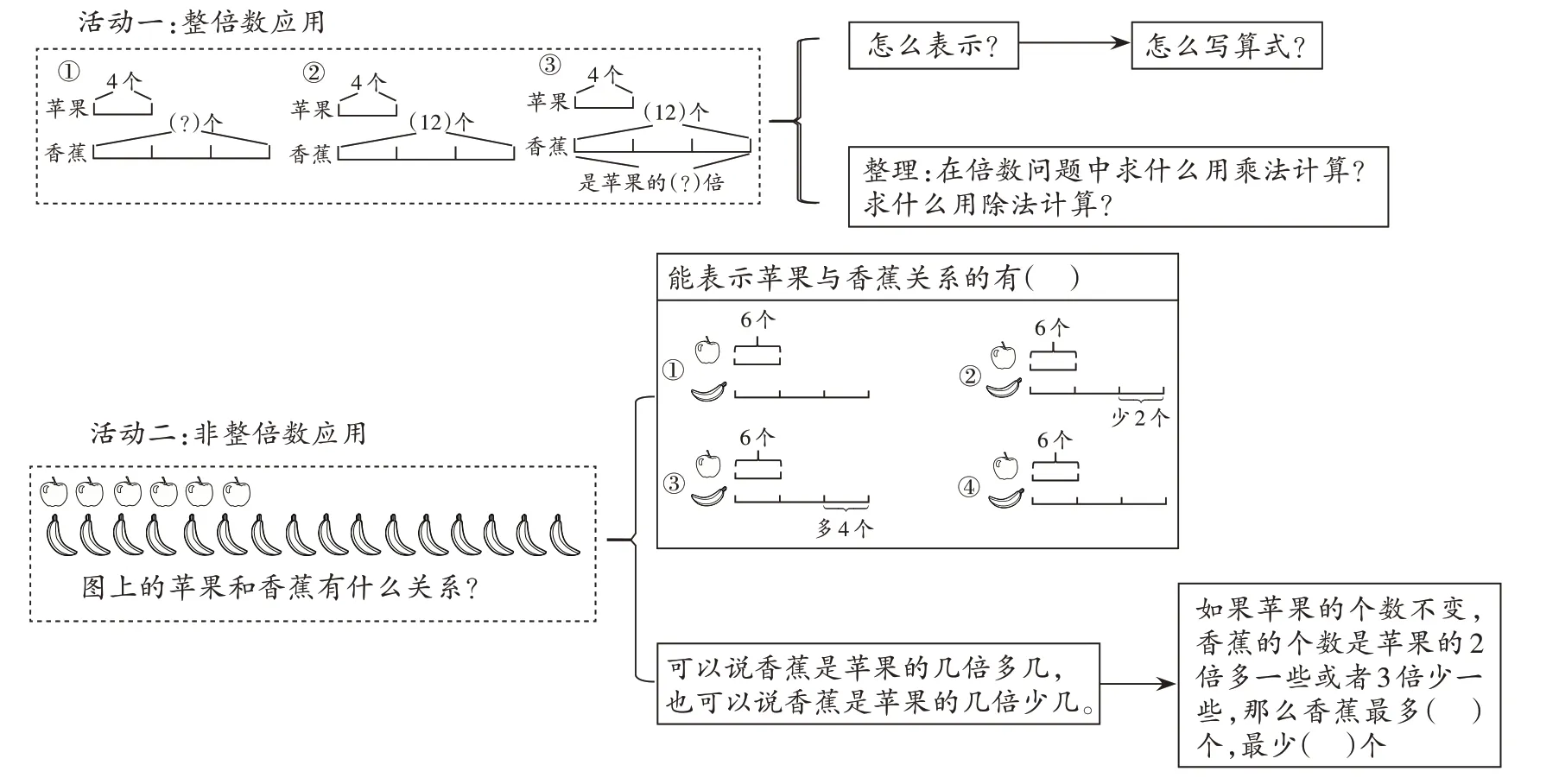
图6 第3课时活动设计

5.经历从“零散”到“结构”的关联过程，促进倍的概念结构形成

在经历了多次比较、扩充概念学习活动后，学生对“倍”的认识虽是连续的，但不够系统。因此在第4 课时设计复习课，以进行沟通和整理。本课时活动一设计如图7所示。

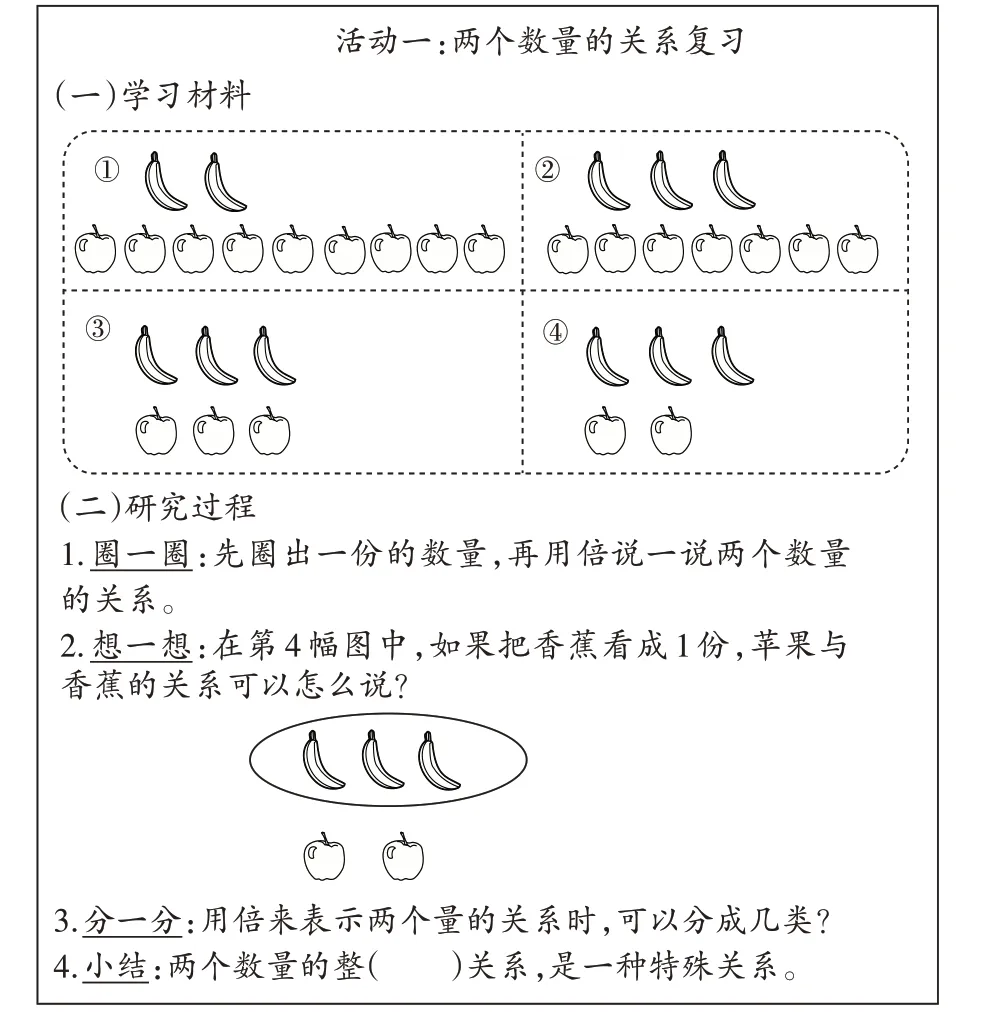
图7 第4课时活动设计

在活动二中，教师列举了4 种不同情境下成倍数的数量关系，旨在让学生活用“倍”的概念解决问题，体验不同情境中倍的表征。虽然在第2 课时中学生对“倍”的三类应用已经有了比较全面的学习，但第4 课时不仅对倍的应用进行了巩固，还和生活中其他倍的应用进行了统整与联系。这不仅丰富了倍的概念的应用，还完善了学生的学习建构体系，使学生达到触类旁通的效果。

（三）阶梯推进：有序促进学生核心素养提升

在本单元的学习中，从用圈一圈来理解倍，到用简单的符号画数量图来解决倍的问题，再到用线段图来解决倍数问题，培养学生的图文转化能力和用画图的方法来帮助思考的意识。整条线层层推进，逐步深入，最终指向核心素养“几何直观”的培养。具体推进路线如图8所示。

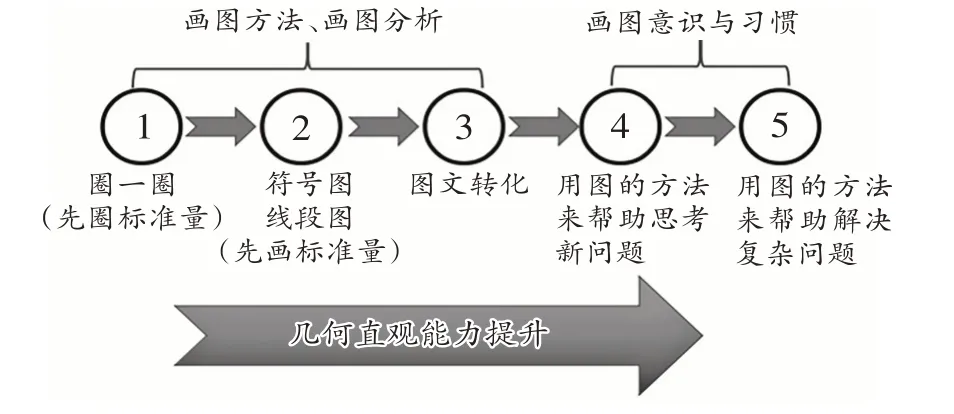
图8 “倍的认识”单元教学推进路线

1.关注标准量：细化画图方法的指导

这个单元指向的核心素养主要是“几何直观”，具体表现为用图来表征倍的能力、用图来培养解决问题的能力和数形结合意识。在前测中，笔者发现利用图形表征能够明显帮助学生更好地理解两数之间的关系，从而解决问题。

先定标准量的指导。在第1 课时中主要指导学生用圈的方法表示倍，引导学生先圈标准量，再圈比较量，有几个这样的标准量就是几倍。在圈画过程中，学生理解了“倍”的概念，建立了“倍”的模型，感受了“倍”与图形之间的联系。

数量图到线段图的指导。在第2 课时中，主要落实从数量图到线段图的指导。对于比较小的数量之间的关系，学生习惯于用数量图的方式呈现其关系。但是数量一旦增大，学生会自然而然地运用线段图代替数量图。在后续的3 个课时中，也持续用线段图表示两数之间的关系，便于更清晰地表达倍的关系，更快地建立“倍”的模型。

2.正逆结合：加强图文转化的训练

在前面的课时中比较侧重对文字转化成图形的指导，即指导学生学会怎么画图。在第3 课时，则侧重对图形转化成文字的指导，让学生看图说意思、看图解决问题、看图编题等。

3.变式运用：新问题中培养画图意识

笔者在教学第4、第5 课时侧重指导学生用画图解决新问题。当学生遇到新问题而束手无策的时候，画图能成为突破问题、厘清数量关系的重要抓手。学生通过画图建立数与形的联系，构建数学问题的直观模型，探索解决问题的思路，有助于把握问题的本质、明确思维。

教学中，教师要对教材进行整体把握，形成抓本质教学的能力，统筹安排，建构路径，阶梯推进，始终以核心素养的培养为目标促进数学教学的实施。