广义塑性本构模型三维化方法的研究与验证

徐家斌,张 博

山东电力工程咨询院有限公司,山东 济南 250013

0 引言

Zienkiewicz et al.[1-2]提出了土体的广义塑性理论,该理论直接定义塑性流动方向张量、加卸载方向张量及塑性模量来构建本构矩阵,并且可以较容易地反映出土的剪胀性、循环荷载变形累积性。由于该理论概念清晰且便于编程实现,近年来在土工领域的应用越来越广泛。在高土石坝的应用中,Xu et al.[3]、邹德高 等[4]对P-Z模型进行改进,并应用于实际工程;陈生水 等[5-6]基于广义塑性理论建立了可以考虑颗粒破碎和循环荷载变形特性的堆石料的广义塑性本构模型;朱晟 等[7]根据高坝室内三轴试验,并结合广义塑性理论推导了可反映防渗土料和堆石料的统一广义塑性本构模型。广义塑性本构模型在构建时使用p、q这2个分量来构成二维应力空间,并以常规三轴试验资料为依据建立土石料的本构关系以预测土工结构的变形特性,但此种在p-q平面建立的本构模型无法反映中主应力的影响[8]。中主应力对土的强度和变形有明显的影响,对于高土石坝的空间分析,不考虑中主应力的影响会使结果有较大误差[9]。因此,各模型在建立时,为能更好地模拟三维应力状态均引入了一种三维化方法。但模型的三维化方法众多,各模型均未针对多种三维化方法进行对比,因此本文基于新疆某面板堆石坝的真三轴试验资料,研究各种三维化的方法应用于广义塑性本构模型的适用性。

1 筑坝土石料广义塑性本构模型及三维化方法

1.1 模型简介

土石料具有非线性、剪缩(胀)性、压硬性、静压屈服以及循环荷载累积性等主要变形特性。以往模型均仅针对某几种主要变形特征推导而成,如邓肯E-B模型和修正的剑桥模型无法体现土石料的剪胀性,使得其计算结果偏大。2个模型均无法准确得到卸载、再加载等应力路径的影响,同时也不能得到循环荷载所产生的变形累积,其仅可用于土石坝的静力有限元分析。在上述2个模型静力分析的基础上,动力分析时需要再采用等效线性模型,这样土石坝的全周期计算需要采用多种本构模型,人为地割裂了土石坝的建设运营阶段,很难对土石坝进行精确的结构分析。筑坝土石料广义塑性本构模型基于广义塑性力学理论,可以较容易地反映出土石料的各种主要变形特性,并且可以基于一套模型参数模拟出土石坝的静力和动力特性,使其受力状态不再进行人为割裂和传递。本构模型推导如下。

大量试验成果表明,高围压下颗粒破碎使得堆石料的强度降低,采用破坏应力比Mf和平均应力p的幂函数关系描述其强度特性。

(1)

式中:参考应力pr=pa+σc,其中pa为大气压,σc为抗拉强度;Mf0和nf为模型参数。

为描述土石料的剪胀性,定义剪胀、剪缩转换时的广义剪应力q和平均应力p的比值为剪胀应力比Mc。通过对堆石料、砂砾料和砾石土料三轴试验结果的整理,认为q和p具有良好的线性关系,由此可得:

(2)

剪胀方程dg采用Lagioia建议的函数[7]。

(3)

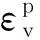
土石料的压缩性可通过等向压缩试验结果反映为:

(4)

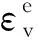
土石料的弹性模量为:

(5)

式中:泊松比ν可取常数,对于堆石料一般取值为0.3～0.35。结合ν便可得到弹性矩阵De。

加载时的塑性流动方向为:

(6)

为模拟卸载体缩,定义卸载时的塑性流动方向为:

(7)

采用非相关联流动法则,加载方向为:

(8)

加载时的塑性模量如下。

(9)

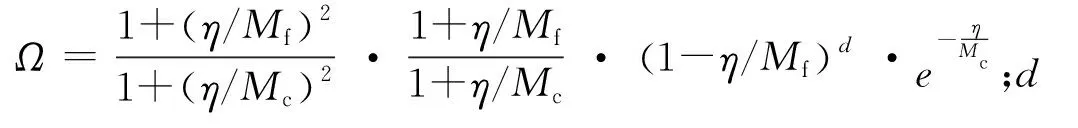
复杂加载条件下,再加载塑性模量如下。

(10)

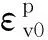
卸载时的塑性模量表示为:

(11)

式中:ηu为上次卸载发生时的应力比;γu为无量纲参数。

1.2 三维化方法

本构模型在建立时,为方便推导通常使用p、q这2个应力参量在p-q坐标系中拟合满足试验条件的等值面(屈服面),这是一种将三维问题二维化的方法,可以使三维问题直观地表示在平面上,但这种方法得到的本构关系与罗德角无关,其无法反映出中主应力对变形的影响。因此,为将本构模型推广到一半应力装置,需将“二维化”的模型重新拓展至三维状态。三维化是一般通过假设其屈服面在π平面上为圆形来实现,模型的剪切屈服和剪切破坏均采用米塞斯准则,例如g(θ)方法。而实际上土石料是一种应力诱导的各向异性材料,其强度遵守摩擦规律,在π平面上并非圆形,但由于屈服函数较为复责应用较少,但可通过变换应力空间的方法将外凸的三角形变换为圆形并进行三维化,如基于SMP准则的变换应力三维化方法[10]和基于广义非线性强度理论(generalized nonlinear strength theory,GNST)的变换应力三维化方法[11]。

1.2.1g(θ)三维化方法

g(θ)三维化方法由Zienkiewice提出[1],该方法认为屈服条件和破坏条件相同,可以实现从剪切屈服到剪切破坏的连续过渡。利用g(θ)三维化方法进行模型三维化的处理方法如下。

(12)

式中:θσ为应力罗德角,J2,J3分别为应力的第二和第三不变量,φf为峰值摩擦角,可通过求解方程(13)得到。

(13)

筑坝土石料的统一广义塑性本构模型提出时,使用该方法进行了模型的三维化处理,但缺少真三轴试验的验证。

1.2.2 基于SMP准则的变换应力三维化方法

Matsuoka et al.[10]提出的基于SMP准则的变换应力法可将二维本构模型推广到一般应力状态为:

(14)

式中:I1、I2、I3为当前应力点对应的3个应力不变量;σij为应力张量,δij为克罗内克符号。

(15)

这样Mf、Mf0、Mc即可用于一般应力状态。

1.2.3 基于广义非线性强度理论的变换应力三维化方法

路德春[11]提出了广义非线性强度理论(GNST),并在此基础上结合变换应力空间的方法建立了一种模型三维化的方法。

(16)

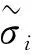
(17)

(18)

GNST变换应力过程可分为2部分:一是将三轴压缩子午面上的非线性破坏曲线变换为过渡应力空间的直线形式;二是将π平面上破坏曲线变换为变换应力空间π平面上的圆。这样便可将广义非线性强度理论变换为扩展的Mises准则。

2 模型验证

2.1 模型参数获取

采用新疆某面板坝的主堆石料的常规三轴试验结果获得筑坝土石料的广义塑性本构模型参数,图1为常规三轴初始加载试验的验证。由常规三轴初始加载试验,通过整理剪胀点和破坏点可以获得Mc、Mf0和nf,对所有试验点进行处理可以得到图1(c),并通过式(1)可以得到剪胀方程参数α和β,因此通过常规三轴初始加载试验可整理出控制塑性流动方向的参数α、β、Mc和控制堆石料强度的参数Mf0、nf。由于缺少等向压缩试验,控制变形大小的参数ct、ce、m、d需要通过反演常规三轴初始加载试验获得,图1(d)反映了变形参数的反演及模型预测结果验证的过程。由图1可知,该模型可以较好地拟合常规三轴初始加载试验结果。

图1 初始加载试验验证

围压为3.1 MPa的试验组同时进行了卸载-再加载试验,如图2所示。控制卸载-再加载过程塑性模量改变的参数为γDM、γden、γu,3个参数需要通过反演卸载-再加载试验获得。图2(a)为直接通过反演得到的模型预测曲线和试验点的比较,模型预测曲线比卸载-再加载试验产生的应变量大,说明模型在卸载和再加载过程中计算所得的模量值比实际情况低。卸载和再加载的试验点较初始加载时稀疏,说明该过程中的加卸载速率较大,而该模型无法反映加载率的相关性,因此拟合效果不理想,而在动力有限元计算中,加载速率的影响可通过阻尼来消耗。许多研究指出,在快速加载时散粒体材料的变形模量可以增大1.1～3倍[12]。为排除加载速率的影响,在反演结果的基础上将卸载-再加载过程中的模量放大2倍,其模型预测结果如图2(b)所示。观察图2可知,在去除加载速率影响的情况下,模型可以较好的预测卸载-再加载过程中的应力应变关系。

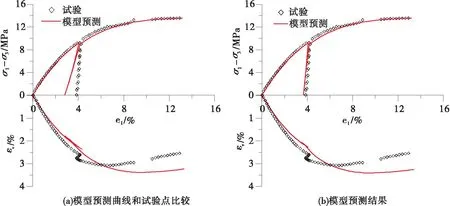
图2 卸载-再加载试验验证

通过对常规三轴试验的验证可以得到该堆石料所有的模型参数,如表1所示。

表1 上游堆石料模型参数

2.2 真三轴试验验证

2.2.1 模型三维化方法比较

模型推导过程中以p、q为应力参量,因此为二维本构模型。进行真三轴试验的验证,应先进行模型的三维化将其扩展到三维应力状态。

图3为3种三维化方法及非三维化在拟合等σ3等b(b=Δσ2/Δσ1,本试验b=0.5,σ3=0.3 MPa,σ1、σ2、σ3分别为第一、二、三主应力)试验的对比图。本材料进行了2组三轴拉伸平行试验,可得参数qe/qc取值为0.68～0.75,考虑到参考应力pr取值较小,为消除试验数据受仪器精度的影响,通过反演拟合单组真三轴试验数据进行验证,当qe/qc=0.7时可以得到较好的结果。观察可知,GNST三维化方法拟合效果最好,g(θ)法和SMP法所得曲线表现出过早的剪切破坏,若不进行模型三维化,在有限元分析中所得的结构变形量偏小,在高土石坝设计分析中是不利的。

图3 模型三维化方法比较

2.2.2 试验验证

采用GNST三维化方法对等σ3等b真三轴试验资料进行模型的验证,试验中b=0.5。由图4可知,模型预测结果与试验点分布吻合较好。该真三轴试验的应力路径比较接近坝体的内部的应力变化,因此该本构模型可以用于高土石坝的有限元分析。

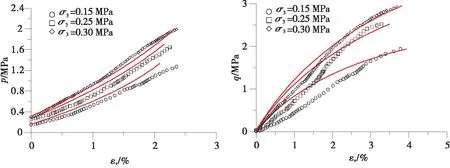
图4 真三轴试验验证

3 基于实测资料的对比分析

3.1 工程简介

新疆地区的某面板堆石坝最大坝高164.8 m,坝顶长795 m,坝顶高程1 825.8 m;坝基为以砂砾石为主的深覆盖层,覆盖层最大厚度约为94 m。为真实反应坝体应力变形规律,将覆盖层与坝体一起构建有限元模型,模型如图5所示。

图5 某面板堆石坝计算模型

为反映出三维化前后的差异,分别进行了非三维化计算和GNST三维化方法的计算,所用模型参数见表2,由于缺少其他3种石料的三轴拉伸试验资料,qe/qc均取0.7。

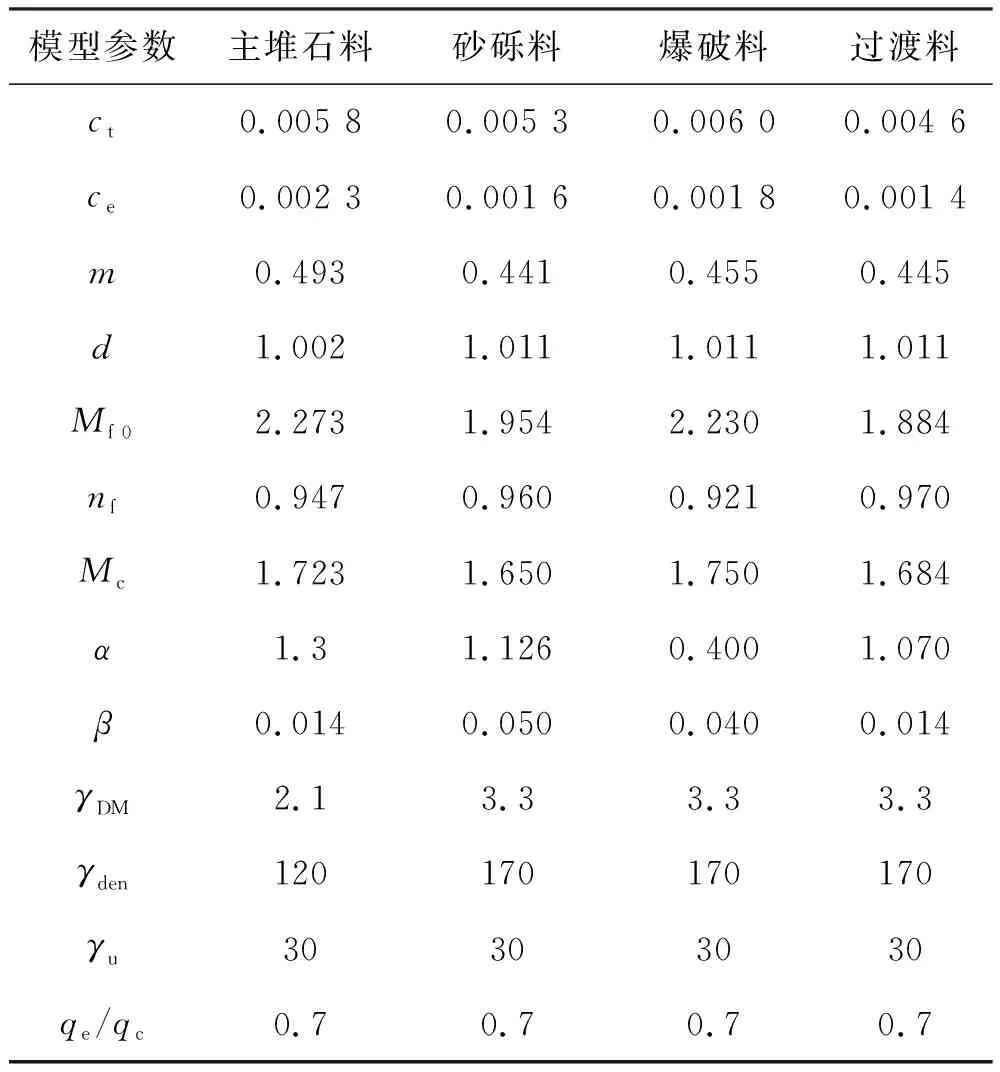
表2 广义塑性本构模型参数

3.2 计算结果分析

3.2.1 模型三维化前后计算结果的比较

图6和图7为模型非三维化及基于GNST方法三维化前后的位移计算结果。由图可以看出,模型三维化前后坝体变形规律基本一致,符合碾压土石坝的一般变形规律,进一步说明筑坝土石料的统一广义塑性本构模型可以较好地反映出土石料的变形特征。模型三维化后的最大竖向位移和水平位移均比非三维化计算值较大。三维化后最大竖向位移所在位置较低,其覆盖层顶部坝底区域的变形较大,而非三维化模型计算值在坝体1/3坝高范围内变形顺速缩小。由于坝体区域土石料具有较高的中主应力,会使土石料表现一定静压屈服,进而拥有一定的变形量,因此模型三维化后的计算结果可以反应出中主应力的影响。

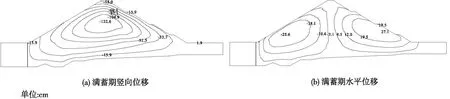
图6 模型非三维化的计算结果

图7 基于GNST方法三维化后的计算结果

3.2.2 计算值与监测值的比较

为监测大坝建设和运行期的变形,进而实时分析其安全性能,进行了监测系统设计。本文取典型断面(0+475)竖向位移监测值与仿真计算结果进行对比,监测点高程分别为1 671、1 710、1 751、1 792、1 822 m。

竣工期和满蓄期有限元分析的计算值和坝体监测值对比结果如图8所示。高程1 760 m以上范围内的坝体三维化计算值与非三维化的计算值接近,且二者与实测值也较为相近;此区域位于坝体上部,该范围内的堆石围压较小(1 760 m高程处σ2≈0.8 MPa),说明在小围压条件下坝体变形可以忽略中主应力的影响。高程1 760 m以下范围内坝体的变形计算值受模型三维化影响较大,三维化计算值较高,在覆盖层顶面竣工期和满蓄期二者相差34.5、38 cm,此差异已无法忽略,该范围内的实测数据略低于三维化计算值;此区域位于坝体中下部,该范围的堆石围压较大(坝底处σ2≈1.6 MPa),其变形受中主应力影响较大。

通过计算表明,在小围压条件下中主应力影响较小,可忽略不计;当围压较高时,中主应力对坝体变形影响较大,若不考虑其影响会使得计算值较小,有限元分析的预测结果较危险;该规律与图3室内试验分析所得规律一致。通过和监测值的对比,说明基于GNST的模型三维化方法可较好的反映出坝体的变形规律,进而为后续工程实践提供理论依据。

4 结论

本文通过真三轴试验和坝体监测数据对筑坝堆石料统一广义塑性本构模型的三维化方法进行了研究,得到以下结论。

1)以p、q为应力参量的二维本构模型忽略了中主应力的影响,直接用于高土石坝的设计将使坝体中下部的计算变形量偏小,在设计阶段对土石坝的安全评价不利。

2)基于GNST的模型三维化方法,可以较好反映等b条件的一般应力状态,此应力路径接近坝体施工运行期的实际应力变化;通过与坝体监的测资料对比,该方法可以较好地反映出坝体变形规律。