基于太阳角度模型和兼具精度-稳定性的光伏发电组合预测方法
王晓龙
山西省智慧交通研究院有限公司,山西 太原 030032
0 引言
风、光等新能源发电功率的精确预测对于制定经济可靠的电力调度计划至关重要[1-3]。新能源发电预测主要有模型驱动和数据驱动2种方法。数据驱动方法主要有支持向量回归(SVR)、多层感知机(MLP)神经网络、集成树模型、长短期记忆(LSTM)神经网络等,其中MLP在新能源出力预测应用较为广泛[4]。而XGBoost、LightGBM以及随机森林等方法因其建模能力强且不容易过拟合,在新能源出力回归预测获得了广泛应用。然而树模型对于高维稀疏特征建模较为困难,且算法参数过多,调参复杂,使用难度较高。LSTM、门控循环单元(GRU)等可提取时序信息,相比MLP的点对点映射模型,在光伏发电的短期和超短期预测方面具有独特优势[5]。由此可见,单个预测模型有各自的优势,若将其进行组合预测,可发挥不同预测模型的优势,相比单个预测模型具有更高的精度和稳定性[6]。
数据驱动方法大多从模型结构和超参数优化角度提高预测精度,较少从提高数据有效信息的角度进行思考。基于数值天气预报(NWP)和数据模型直接建立起气象预报和功率映射是一种常见的新能源发电功率预测方法。然而NWP中关于辐射的预报通常只包含水平辐射通量,即单位水平面接收到的总辐射量,包括太阳的直接辐射和空气的散射。倾斜的光伏板所接收的辐射量受太阳光入射角、直接辐射量以及空气散射量影响。文献[7]在基于气象预测和光电转化模型的光伏发电短期预测中,将光伏板倾角对辐射的影响纳入了考虑范围。文献[8]使用12种直散辐射分离模型和斜面辐射模型的组合来计算倾斜光伏板的辐射强度,然后基于拟合的光电转换系数预测发电功率。然而这2种方法均需要较多模型参数(如光伏板倾角),且须先将水平辐射转化到斜面辐射,进而根据光电转换系数预测功率,增加了预测步骤,降低了预测精度。
综上所述,本文考虑在太阳方位角度的基础上建立包括点预测和时序预测的模型,提出一种基于太阳角度模型和数据的光伏出力组合预测方法,贡献如下:首先,基于太阳角度模型,求解出不同时刻气象预报对应的等效太阳入射角度数据,可有效提高数据驱动模型预测精度;然后,分别采MLP、XGBoost和lightGBM等点预测模型以及LSTM、GRU、双向LSTM(Bi-LSTM)和卷积LSTM(C-LSTM)等时序预测模型对光伏出力进行预测,可同时有效提取历史数据与发电功率之间的单点和趋势映射关系;最后,提出了基于偏差-方差权重的组合方法,将点预测模型和时序预测模型的预测结果进行融合,在进一步提高预测精度的同时,有效降低了预测方差。
1 太阳入射角度建模
1.1 固定光伏板辐射分析
光伏板一般分为固定光伏板与追日光伏板,固定式的光伏板造价和维护成本都较低,因此在屋顶光伏项目和绝大部分光伏电站获得了广泛应用。单位面积固定光伏板发电功率主要取决于光伏板总辐射通量和太阳角度。24 h太阳方位角(时间角)θt和高度角θh随时间变化,如图1所示。方位角θt为太阳光在水平面上的投影与正南方向的夹角,高度角θh为太阳光与水平面的夹角,太阳光入射角度(简称“太阳角度”)可由θt和θh描述。
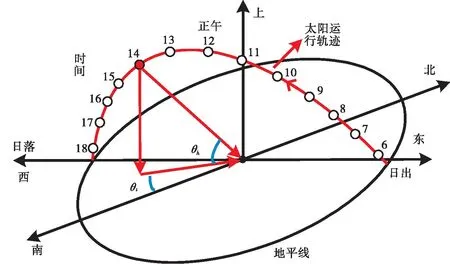
图1 太阳方位角θt和高度角θh在一天中的变化
1.2 太阳方位角的求解
太阳方位角θt随时间的变化可由以下公式计算。
(1)
式中:h、m分别为北京时间的小时与分钟,24小时制;θt在12:00为0°,每增加或减少1 h,则相应增加或减少15°,6:00为-90°,18:00为+90°;θt0为当地时间与北京时间的差值,取决于光伏电站所在地的经度。因此θt可由时间直接计算出来。
1.3 太阳高度角的求解
太阳高度角θh的计算公式如下[9]。
sin(θh)=sin(φ)×sin(δ)+cos(φ)×cos(δ)×cos(θt)
(2)
式中:φ为光伏发电站的纬度;δ为赤纬,即地球上太阳直射点的纬度,春分和秋分0°,夏至23°27′,冬至-23°27′。
太阳赤纬δ的一种高精度计算方法如下[10]。
δ=0.006 918-0.399 912×cos(b)+0.007 025 7×
sin(b)-0.006 758×cos(2b)+0.000 907×sin(2b)-0.002 697×cos(3b)+0.001 48×sin(3b)
(3)
(4)
式中:N为积日,即一年之中的第几天。根据式(2),对于特定的电站或者电站群来说,其纬度φ和时区时差θt0是定值。可以证明,该值即使有一定误差或者使用任意假设值时,其固定误差可同样视为预测模型的隐含参数,仍然不影响最后的预测精度。太阳赤纬δ可由采样时间直接计算出来。最后将太阳方位角θt和高度角θh作为预测模型的特征,输入到神经网络和随机森林等模型进行功率预测。
2 基于偏差-方差权重的组合模型
在基于MLP、树模型、LSTM以及GRU等不同数据驱动模型对光伏出力进行预测之后,为结合不同预测模型的优势,将不同模型的预测结果进行加权得到最后的融合模型。分配权重的基本原理是优秀的模型分配更高的输出权重。
基于方差协方差(VC)的组合优化将模型i预测方差Vi的倒数1/Vi作为该模型的输出权重,当预测误差呈现高斯分布时,根据加权最小二乘估计,最优权重是预测方差Vi的倒数[11],即1/Vi。由于实际中,预测误差可能不一定服从高斯分布,其偏差不一定为0,此时最优权重将不再是1/Vi。因此,本文提出基于预测偏差和方差进行预测模型的权重分配。

(5)

第i个模型的预测方差为:
(6)
第i个预测模型输出权重为wi,加权融合预测值为:
(7)
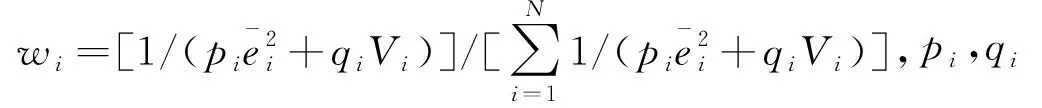
3 算例分析
3.1 数据说明
本文选取不同地区4个额定容量分别为130、110、100、50 MW的光伏发电场2020—2021年这2年光伏发电数据及其对应气象预测数据作为算例验证。光伏发电数据以及对应的NWP气象预报间隔为15 min,每天96个预测点。每个NWP预报包括22个气象特征,分别为:温度、短波辐射通量(单位水平面)、长波辐射通量(单位水平面)、温度(2 m)、云量、相对湿度(2 m)、风速(70 m)、风速(100 m)、风向(30 m高度)、风向(70 m)、动量通量、气压(海平面)、潜热通量、感热通量、水压(地表)、大尺度降水、总降水、对流降水。基于Pearson相关系数,与发电功率相关性从高往低前6个气象特征为:短波辐射通量、感热通量、潜热通量、2 m相对湿度、2 m温度、长波辐射通量。每次训练时将数据集的70%作为训练集,15%作为验证集,15%作为测试集,基于python机器学习库实现本文提到的深度学习算法。
3.2 误差指标
本文采用相对容量误差对预测效果进行评价。相对容量均方根误差ECRMES可用来衡量预测均方根误差相对设备发电容量的大小。
(8)

3.3 太阳角度特征和单模型的功率预测
为验证特征筛选和新增太阳角度(太阳方位角和高度角)特征的效果,分别将如表1所示不同的特征组合作为模型输入进行模型训练。在单模型发电功率预测测试中分别建立了如表2所示的7种模型。对这7种模型使用不同的特征输入对未来7 d光伏出力进行多次训练和预测,7种模型的预测误差平均值如表3所示。

表1 不同模型、特征组合的相对容量均方根误差

表2 7种预测模型超参数说明
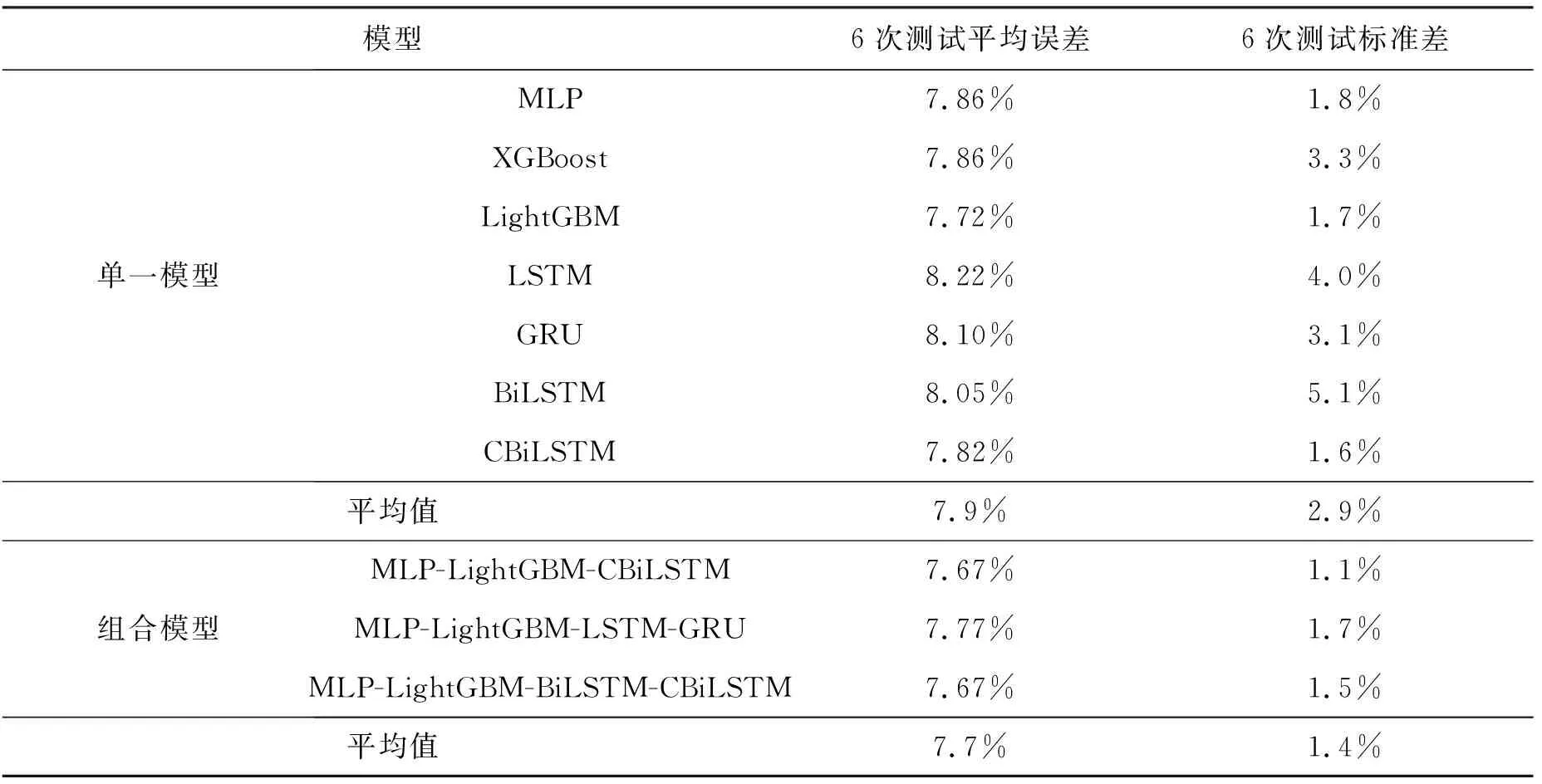
表3 单一模型和组合模型的预测误差、标准差对比
从表1可以看出,在不使用太阳角度特征、仅使用NWP气象特征时,lightGBM、CBiLSTM等7个单模型“使用前6个筛选特征”的预测误差(平均7.65%)小于“使用所有的22个NWP气象特征”的预测误差(平均7.75%)小于“仅使用短波辐射”的预测误差(平均8.76%)。测试结果表明了更多的气象特征有助于提升预测精度,然而低相关特征过多反而导致精度有所降低,因此将原始特征进行筛选或者降维有助于提升预测精度。同理,“短波辐射通量和太阳角度”(平均7.67%)小于“仅短波辐射通量”(平均8.67%),以及“22个气象特征和太阳角度”(平均7.47%)小于“所有22个气象特征”(平均7.75%),表明了增加太阳角度后可有效降低预测误差,且在仅有短波辐射特征时,太阳角度特征的加入使预测误差降低了11.5%。
3.4 单模型与组合模型不同时间尺度预测测试
为了避免随机性造成的误差,在模型融合测试中对每个单模型均采用不同参数进行多次训练,然后通过选择测试集中表现较好的模型基于提出的预测方差-偏差方法进行融合,方差-偏差权重均为0.5,最后使用测试集来最终评价模型融合效果。本次测试中,输入特征组合为6个筛选特征加2个太阳角度特征。为了验证融合模型的效果以及不同融合方法的效果,本文分别将7种表2所示的单模型以及3种模型组合预测对未来1、3、5 d总共6次测试,测试结果如图2和表3所示。

图2 单一模型和组合模型预测相对容量均方根误差和标准差
图2和表3显示,单个预测模型的相对容量误差为7.6%~9%,平均误差为7.9%,平均标准差为额定容量的2.9%。本文提出的组合模型的预测误差位于额定容量的7.4%~8%,平均为7.7%,平均标准差为额定容量的1.4%。对比结果显示了本文提出的组合模型较单个模型具有高精度、低预测方差(预测更加稳定)的优势。提出的基于偏差-方差的组合预测模型相比单个模型的预测误差平均降低了约3%,预测标准差从额定容量的2.9%降低到了1.4%,降低了约50%。
不同时间尺度的光伏出力连续预测结果如图3所示,可以看出在不同预测尺度下基于太阳角度与模型融合的预测效果均比原来特征单一模型预测更加接近真实发电曲线。由于光伏发电在正午时受对阴影较为敏感,此时发电随机性更大,更加难以预测。同时也可看出,在正午发电峰值时,加入太阳角度特征的组合模型预测精度也更高,也证明了本文提出方法的有效性。

图3 光伏发电预测测试图
4 结束语
本文在现有研究方法上提出一种基于太阳角度模型以及偏差-方差权重的光伏发电组合预测方法。所提出的太阳角度仅需根据时间和太阳运行模型即可求解,在气象特征较少的情况下对预测精度有较大幅度的提升。同时本文提出偏差-方差融合法将多种预测模型融合,算例证明改进多模型融组合预测更加稳定且精度更高。

