满约束轴向拼接张拉整体结构的自稳定性分析

刘贺平, 王艳蒙, 曹紫莺, 罗阿妮, 王焰新

(1.哈尔滨工程大学 机电工程学院, 黑龙江 哈尔滨 150001; 2.上汽通用汽车汽车有限公司武汉分公司, 湖北 武汉 430208)

张拉整体结构是由受拉索构件相互连接形成的索网结构被离散的受压杆构件从内部撑起所形成的一种自应力空间结构[1-3]。张拉整体结构以柔性构件为主,刚性构件不直接接触,结构整体具有一定的弹性[4-6],其刚度也可以通过改变个别构件的张紧程度来调节[7]。构件运动耦合度高,可以通过少数构件驱动整体运动。结构中不存在传统的运动副形式,构件间位姿变化更为灵活[8]。

目前,许多研究人员正在尝试将张拉整体结构转化为机构[5,9-10],以获得更多机构构型,完成传统机械无法实现的功能。在将张拉整体结构转化为机构时,研究人员更趋向于对称性好、构件分布更为规则的张拉整体结构作为研究对象[11],以减小设计、加工和控制难度。利用张拉整体单元或者小的刚性结构拼接形成更为复杂的张拉整体结构是张拉整体结构主要构型方法之一,也易于保证构建结构的对称性[12]。杜纹娟[13]对基于张拉整体的可变结构体机器人进行了研究,对张拉整体结构构型做了选择与结构参数优化。马瑞嘉等[14]对张拉整体式高耸结构进行优化研究,是张拉整体在竖直方向上的一种应用。袁行飞等[15]对环形张拉整体结构进行应用研究,丰富了张拉整体结构形式及其应用。王雅峰等[16]采用混合整数规划的方法对张拉整体进行拓扑找形研究。袁行飞等[17]对大跨度张拉整体式穹顶进行了研究分析,为张拉整体结构在大跨度空间结构领域应用提供基础。王征[18]对张拉整体结构的找形和稳定性进行了分析研究。李冰玉等[19]设计一种基于张拉整体结构的连续型机械臂,此机械臂是由多个类似剪式铰单元拼接而成,外附绳索以起到加固等作用。张晨阳[20]提出了一种张拉整体式伸展臂,此伸展臂是由多个三杆张拉整体单元轴向拼接而成。

拼接方式形成复杂张拉整体结构,由于其结构对称性好,探索保证结构稳定的参数关系,有助于获得更多构型和拓扑结构。本文将基于结构的平衡方程,以一种新型的满约束张拉整体轴向拼接结构为对象,研究保证张拉整体拼接结构自稳定的参数关系的获取方法。

1 张拉整体基本单元

三杆张拉整体单元是张拉整体结构的基础[21],此单元可以拓扑为具有更多杆构件的张拉整体单元[22],也可以通过拼接,形成更复杂结构的张拉整体结构[23]。

三杆张拉整体基本单元如图1所示,图1中粗线表示杆构件,细线表示索构件。此结构包括3根杆和9条索,上下端面所在平面平行,上下端面形心连线(即结构轴线)垂直两端面,同一端面3根索构件围成正三角形。设此三杆张拉整体单元的上端面圆周半径为ru、下端面圆周半径为rd、端面间高度为h。索构件分为3类,即上端面水平索、下端面水平索、连接两端面节点的斜索。设上下端面的相位角为φ,称此角为单元内扭转角(这一角度为任意一根杆构件的2个端点在底面上的投影与底面圆心的连线夹角)。

图1 张拉整体基本单元结构简图Fig.1 Structural diagram of tensegrity basic unit

2 满约束轴向拼接张拉整体结构

2.1 轴向拼接

利用张拉整体单元轴向拼接形成的结构如图2所示,拼接时相邻单元的杆构件旋向相反,即单元内转角相加为360°,目的是当结构受到轴向力时,各单元的转动会抵消,从而使结构两端面间不会发生相互转动,相邻2个单元在轴向有一定的重叠交错以保证2个单元之间固定的稳定可靠。如图2所示,与单个单元相比,下单元的上水平索和上单元的下水平索被去除,重新连接,称重新连接后的索构件为鞍索(即索n4n7、n5n8、n6n9、n7n5、n8n6和n9n4),同时也添加了连接2个单元的索构件,即附加索(索n1n8、n2n9、n3n7、n6n10、n4n11和n5n12)。

图2 2个三杆张拉整体单元轴向拼接结构Fig.2 Axial splicing structure of two three bar tensegrity units

这样的拼接方式能够使张拉整体单元牢固稳定以形成一个整体,但是在分析计算保证结构稳定的参数条件时也存在节点约束过多的问题。

2.2 满约束拼接

以图2所示结构的n5点为例,连于此节点处有1根杆构件和4根索构件。一个节点上受到5个构件施加5个力作用来达到平衡,此节点属于过约束,利用力平衡方程求解构件内力是多解的。

为了减小节点受力过约束数目,采用减少固定于节点的构件数来实现满约束拼接(节点非过约束)。

张拉整体结构的索构件都位于结构表面,节点n5连接4根索构件的内力的合力会有将此节点向结构内部拉的趋势,而杆构件施加向外支撑力以平衡此节点,因此,连于此节点上的杆构件的作用其他构件无法替代,不能去除。连于此节点的鞍索和附加索,都是起到将2个相邻单元连接固定在一起的作用,只有斜索是属于一个单元内部的,而且附加索也可以提供斜索施加于此节点的轴向力,因此这里尝试将斜索去除以获得新的稳定构型。

去除斜索后,图2所示结构的每个节点上只连有3根索构件,利用节点力平衡方程,可以建立每个节点的索构件内力与杆构件内力的关系式,这里称此无斜索结构为满约束结构。

3 满约束轴向拼接构型分析

3.1 满约束结构节点广义坐标矩阵

根据相邻2个单元的单元内转角的关系,可以形成图3所示的2种满约束结构。图3(a)所示结构的上下2个单元的单元内扭转角φ相等,图3(b)所示上下单元的单元内转角φ互为相反数(或2个单元内转角和为360°),拼接的2个单元的端面半径和高度都相同。图3(c)中,θ为上下2个单元之间的单元间转角(即2个单元间的相位角,节点n7与节点n1在底面投影与原点连线之间的夹角),φ为单元内转角(节点n4与节点n1在底面投影与原点连线之间的夹角,即单元上下端面间相位角,图3(c)所示为下单元的单元内转角),α为下单元上端面起点n4与上单元下端面起点n7在底面投影与原点连线之间的夹角,3个角满足θ=φ+α。

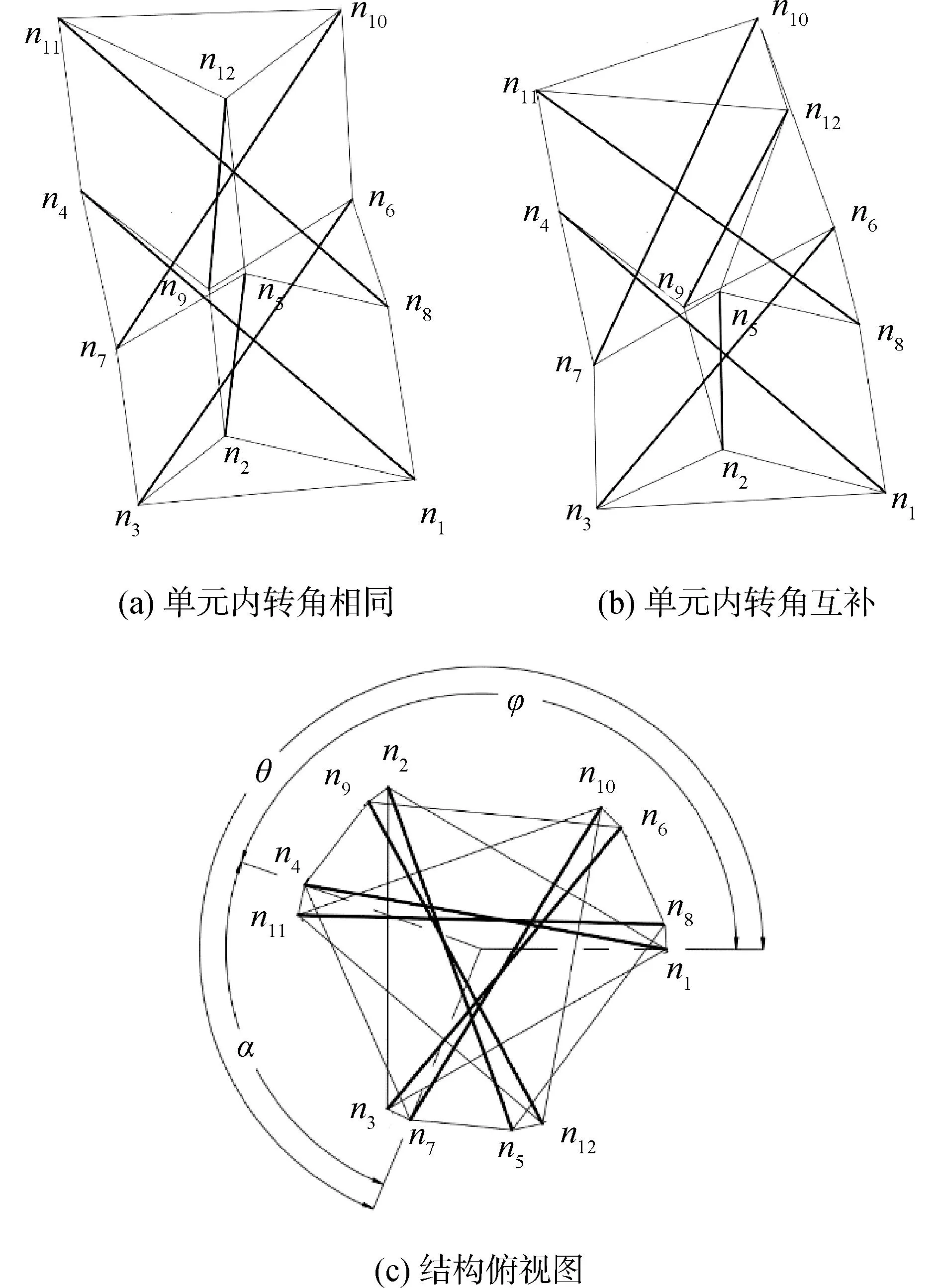
图3 满约束轴向拼接结构Fig.3 Fully constrained axial splicing structure

以图3(a)所示结构为例,基于节点受力平衡,分析保证此类结构稳定时需要满足的结构参数关系。

图3所示的满约束张拉整体结构的每个节点只连接1根杆构件,所有构件只承受轴向力,即每个构件的内力与构件向量相同,因此建立平衡方程需要首先确定构件向量。构件向量由构件端点确定,下面首先计算各节点坐标。

结构第1层节点坐标可计算为:

(1)

式中r1为节点所在第1层端面圆半径。

第2层节点坐标的计算公式为:

(2)

式中:φ为单元内转角;r2为节点所在第2层端面圆半径。

第3层节点坐标列向量的表达式为:

(3)

式中:θ为单元间转角;重叠率k为两单元之间重叠部分与单元高度的比值;r3为节点所在第3层端面圆半径。

第4层节点坐标可计算为:

i∈{10,11,12}

(4)

式中r4为节点所在第4层端面圆半径。

该满约束结构的节点矩阵可表示为:

(5)

3.2 满约束结构构件连接矢量矩阵

图3(a)所示结构的杆构件与节点连接关系如表1所示。

表1 满约束结构杆构件与节点连接关系Table 1 Connection relationship between member and node of fully constrained structure

杆构件矢量矩阵可表示为:

(6)

(7)

如前所述,图3(a)所示满约束结构的索构件分水平索、鞍索和附加索3类。水平索与节点间的关系如表2所示。

表2 水平索与节点的连接关系Table 2 Connection relationship between horizontal cable and node

水平索矢量矩阵可表示为:

(8)

(9)

鞍索与节点的连接关系如表3所示。

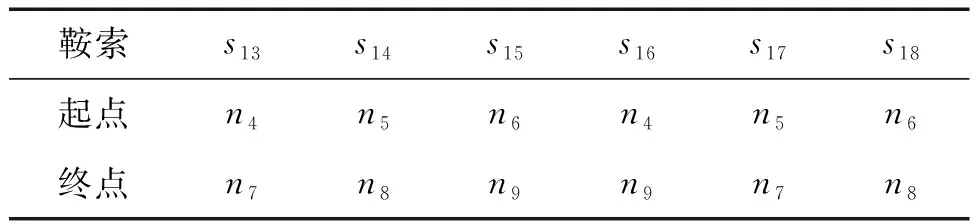
表3 鞍索与节点的连接关系Table 3 Connection relationship between saddle cable and node

鞍索矢量矩阵SII可表示为:

(10)

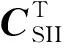
(11)

附加索与节点的连接关系如表4所示。

表4 附加索与节点的连接关系Table 4 Connection relationship between additional cable and node

附加索矢量矩阵可表示为:

(12)

(13)

满约束结构所有索构件矢量矩阵可表示为:

(14)

(15)

3.3 满约束结构力平衡分析

满约束结构任意一个节点都连接3根索构件和1根杆构件,每个节点受到4个构件内力作用。杆构件的内力可表示为:

|FBi|=λi·|bi|

(16)

式中:FBi为第i根杆的内力;λi为第i根杆的杆构件力密度。

将杆构件的内力分配于各节点后形成杆构件力矩阵:

(17)

式中λ为杆构件力密度矩阵。

(18)

同理,将所有索构件的内力分配于节点形成索构件力矩阵:

(19)

式中:索构件力密度矩阵γ同杆构件力密度相似是个18×18方阵,对角线元素依次为各索构件力密度,其余元素为0。

结构稳定时,其各节点上所受合力为0,即:

(20)

4 满约束轴向拼接结构自稳定性实例分析

4.1 方式一

式(20)为基于节点力平衡所建立的整个结构的力平衡方程,通过此方程的求解来获得结构平衡时参数之间的关系。由于式(20)较为复杂,求解难度大,而且平衡方程系数矩阵(即平衡矩阵)也不是方阵。为减小求解难度,将平衡矩阵转化为方阵,这里将平衡方程进行缩减。由图3可知,满约束结构的每个节点上连有3根索和1根杆,即一个节点力平衡分析时,所建立的以力密度为未知量的平衡方程中应该含有4个未知量,这样获得平衡矩阵的维数为3×4,不是方阵,求解难度大。图3所示结构的上下端面的水平索长度相同,结构的构件内力分布均匀也是结构自稳定的重要保障,即同类构件的内力相同或相差较小,如果这里设同一端面的水平索内力相同,则选择位于上下端面的一个节点列写平衡方程,也可以获得3×3的平衡矩阵。选择2个节点列写力平衡方程时,如果2个节点共用一根索,平衡方程中的力密度未知量为7个,如果其中一个节点位于上下端面,力密度未知量将缩减为6个,也可获得形为方阵的平衡矩阵。选择2个节点时,这2个节点应该位于不同单元,这样才能获得与拼接相关的参数关系。通过选择位于上下端面上一个节点列写平衡方程并求解发现,所获得的行列式表达式无解,因此下面将选择2个节点列写平衡方程。

首先,由图3可知,节点n4和节点n11分别是下单元的上端面节点和上单元的上端面节点,而且这2个节点通过一根附加索相连,这里只保留式(20)中节点n4和n11受力平衡所列出的6个平衡方程,则式(20)缩减为:

(21)

式中:W为平衡矩阵,由W1、W2、W3、W44部分组成。

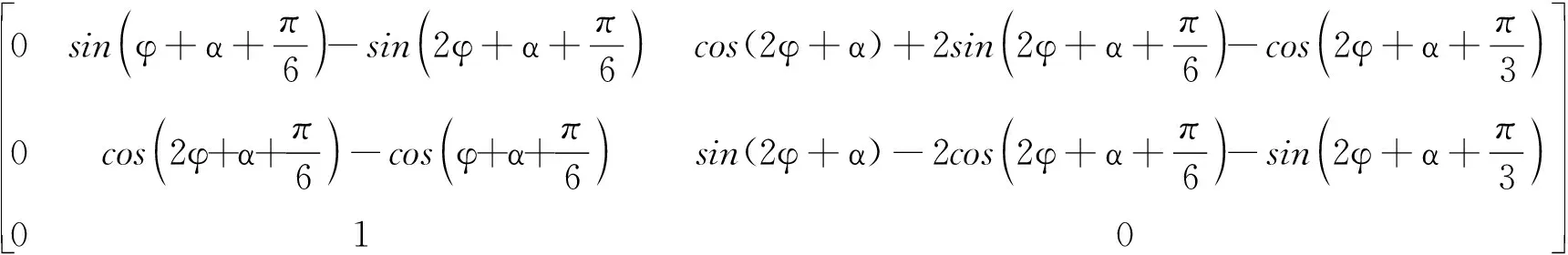
式(21)存在非零解的条件为系数矩阵W的行列式值为0,可获得:

(22)

式(22)只包含了单元内转角φ、单元间转角θ和重叠率k,即此类结构的稳定性只和这3个参数有关。根据式(22)绘制的3个参数之间的关系曲面如图4所示。由图4可知,这3个参数的关系较复杂,无法体现明确的对应关系,但可以获得一些趋势。当下单元的单元内转角φ∈[60°,65°]时,有满足式(22)的几个柱状尖点;当α∈[0°,60°]时,随着单元内转角φ∈[0°,60°]增大时,重叠率k先减小后增大。当α∈[0,90°]时,随着单元内转角φ∈[70°,180°]增大时,重叠率k先减小后增大。

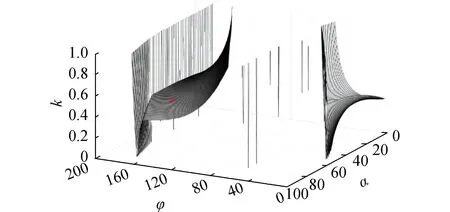
图4 构型参数函数关系三维图Fig.4 Three dimensional diagram of configuration parameter function relationship

根据式(22),取α=70°,φ=150°,得到k=0.461 2。将这3个数据代入节点坐标计算公式,获得构件向量。依据节点矩阵和构件向量所确定的满约束结构的简图和实物模型图如图5所示,并由实物模型可知,此结构是自稳定的。由平衡方程计算获得各构件内力如表5、6所示。由表5、6可知,同类构件内力相同,内力数值相近,力分布均匀,这也是保证此结构能够稳定的重要条件。由此实例分析可以证明,本文提出的构型、分析建立平衡方程的方式、对平衡矩阵的缩减和求解方式正确,也证明应用此方法可以获得稳定构型。

表5 各杆构件内力值Table 5 Internal force value of each bar member

表6 各索构件内力值Table 6 Internal force value of each cable member

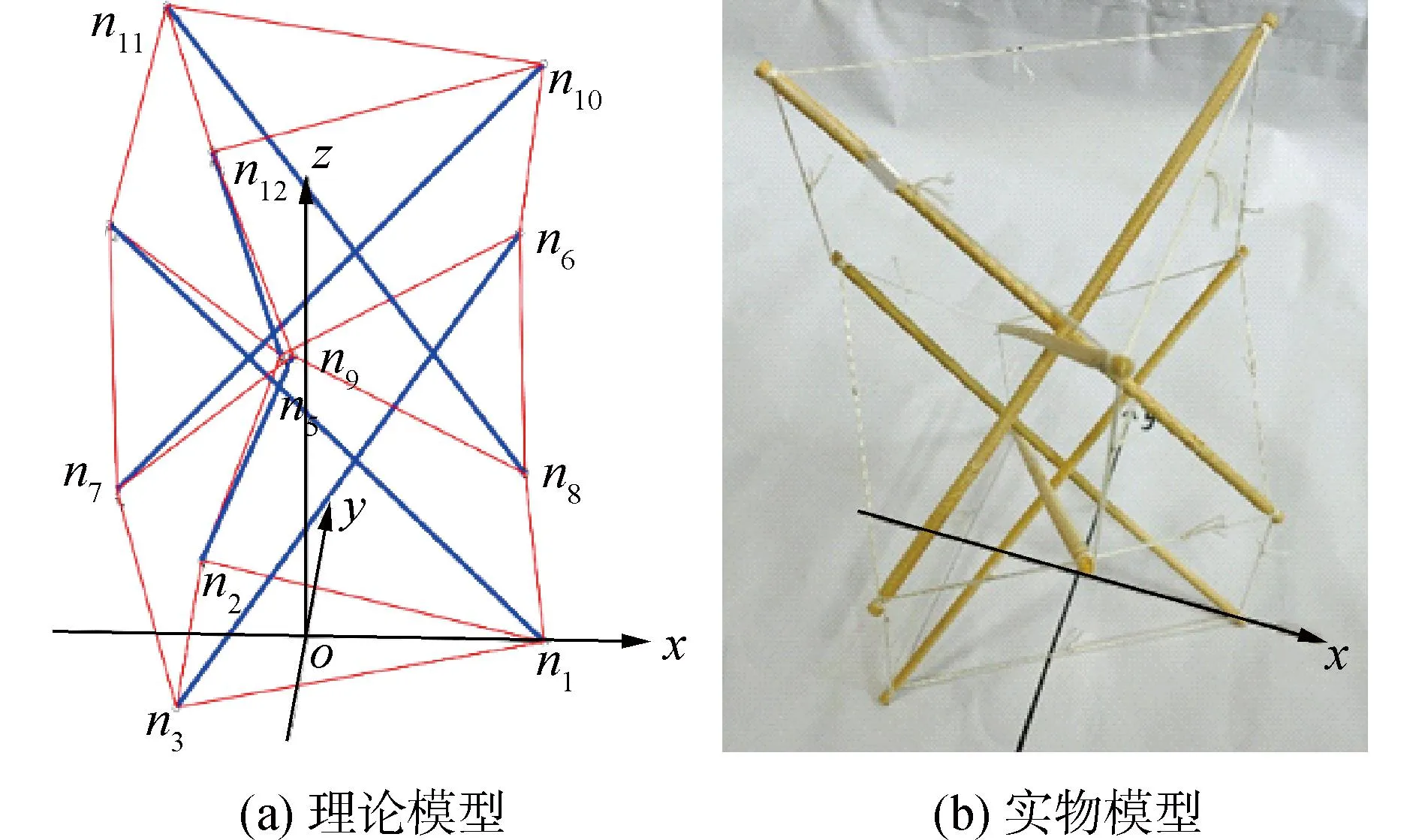
图5 理论模型与实物模型Fig.5 Theoretical model and physical model

4.2 方式二

在第2节中,根据缩减原则,选择节点n4和节点n11列写平衡方程。下面依据缩减原则,选择连于一根附加索,分别位于2个单元下端面的节点n3和n7进行节点力平衡方程的缩减,对缩减原则的正确性进行进一步验证。依据列写的平衡方程获得的平衡方程系数矩阵为:

按照方程有非零解,系数矩阵行列式值为0的原则,获得关系式:

(23)

式(23)体现了单元内转角φ,单元间转角θ和重叠率k的函数关系,此类结构稳定性只与这3个参数有关,根据式(23)绘制的3个参数之间的关系曲面如图6所示。

图6 构型参数函数关系三维图Fig.6 Three dimensional diagram of configuration parameter function relationship

由图6可知,3个参数关系较复杂,体现不出明确的对应关系,仍可以获得相关一些趋势,当单元的单元内转角φ∈[0°, 80°],随着扭转角α∈[70°, 90°]增大时,重叠率k先减小后增大。当扭转角α∈[0°, 40°],随着单元内转角φ∈[0°, 60°]增大时,重叠率k有增大趋势。当扭转角α∈[0°, 30°],随着单元内转角φ∈[70°, 140°]增大时,重叠率k先减小后增大。当单元间转角φ∈[160°, 180°],随着扭转角α∈[30°, 90°]增大时,重叠率k先减小后增大。

根据式(23),取α=40°,φ=150°,得到k=0.279 1。将这3个数据代入节点坐标计算公式,获得构件向量。依据节点矩阵和构件向量所确定的满约束结构的简图和实物模型如图7所示,由实物模型可知,此结构是自稳定的,各构件内力如表7、8所示。由表7、8可知,同类构件内力相同,内力数值相近,力分布均匀,这是保证此结构能够稳定的重要条件。该实例可证明:本文提出的构型、分析建立平衡方程的方式、对平衡矩阵的缩减和求解方式正确,也证明应用此方法可以获得稳定构型。

表7 各杆构件内力值Table 7 Internal force value of each bar member

表8 各索构件内力值Table 8 Internal force value of each cable member

图7 理论模型与实物模型Fig.7 Theoretical model and physical model

图3(b)所示上下单元内转角φ互为相反数的满约束张拉整体结构,基于节点力平衡建立整个结构的力平衡方程,将相应节点平衡方程进行缩减,计算方程系数矩阵行列式值,求解构型参数关系式无解,此方法无法求解出此类满约束结构构型参数,无法获得稳定构型。

5 结论

1)本文提出了一种依据平衡方程获得张拉整体结构稳定构型的方法。张拉整体结构自稳定时,其以力或力密度为未知量的平衡方程存在非零解,即当平衡矩阵为方阵时,其行列式为0,分析可知,该方法可以获得满足张拉整体结构自稳定的结构参数关系,依据此关系可获得自稳定张拉整体结构;

2)本文提出一种平衡方程缩减方法,该方法通过少量节点坐标可以建立方阵形式平衡矩阵的平衡方程,实例证明该方法具有一定可行性;

3)将轴向拼接张拉整体结构的斜索去除,形成了满约束张拉整体结构,该结构的构件数目减小,节点过约束问题消除,通过搭建实物模型验证此结构具有自稳定性,该构型是一种全新的张拉整体构型,为张拉整体轴向拼接提供新的思路。