基于在线海流数据的自然能驱动无人艇能源最优路径规划

李可, 廖煜雷,2, 刘骁锋, 贾琪, 李相杰, 翟子正

(1.哈尔滨工程大学 智能海洋航行器技术全国重点实验室, 黑龙江 哈尔滨 150001; 2.哈尔滨工程大学 三亚南海创新发展基地, 海南 三亚 572000)

近年来,随着无人艇(unmanned surface vehicle, USV)技术的不断发展[1-9],需要无人艇执行的任务也越来越复杂,诸如海洋资源勘探、环境监测、海上安全等[10-12]。无人艇在执行任务时,通常需要较高的续航能力,但是由于尺寸的限制,无人艇无法携带大量的能源。路径规划是无人艇研究中的核心问题。在执行同样的任务时,不同的路径会产生不同的能源消耗,路径规划问题直接影响到了无人艇的续航力。为了有效提高无人艇续航力,无人艇能源最优路径规划成为了一个研究热点问题。

无人艇路径规划研究通常以到达目标点的距离或时间最短为目标[13-14],最短距离或时间未必会对应最少的能源消耗。为了解决无人艇节能路径规划问题,英国的Niu等采用Tidetech公司的海流数据集,通过建立海流对无人艇的能源消耗模型,利用可见图算法、Dijkstra搜索算法对维诺图算法进行优化,得到能源最优的路径规划方法[15-16],由于该方法只能得到固定流场下节能路径,然后Niu等利用遗传算法(genetic algorithm, GA) 对维诺图进行改进,得到时空变化流场下的能源最优路径规划算法[17]。Niu等使用的Tidetech公司的海流数据集在不同地区的空间尺度和时间更新步长有差异。最短更新时间为1 h,最小空间尺度为800 m。

A*算法也被广泛应用于无人艇的能源最优路径规划中[18-19],Koay等[20-21]通过热带海洋动力学(tropical marine hydrodynamics, TMH)得到动态海流预测模型,利用该模型对A*算法进行优化,得到考虑海流变化的能源最优的路径规划算法[22],该算法使用数据集能提供的海流数据时间更新步长和空间尺度均较大,更新时间为30 min,空间尺度为100 m。周耀鉴等[23]提出了一种基于局部流场构建的水下滑翔机路径规划方法,采用CTS-A*(constant time surfacing A*)迭代算法进行路径规划,在仿真环境下,分别利用该算法对单个和多个流场进行测试,实验结果表明,该算法适用于常规大小海流以及大海流情形。

水平集算法也被广泛地应用于无人艇的路径规划中[24],Lolla等[25-26]利用MSEAS(MIT multidisciplinary simulation, estimation, and assimilation system)对菲律宾海域的海流进行预测,得到该海域海流的预测模型。在水平集算法演化函数构建中加入海流的影响,得到时间最优的路径规划算法。MSEAS能提供不同尺度的海流预测数据,Lolla等的试验证明了海流数据尺度对时间最优路径规划算法的结果影响很大,但是MSEAS能提供的最小空间尺度是1 km。

上述方法均为经典路径规划算法,这类算法的共同点是需要高精度的海岸线和海流数据。通常,越高精度的地图数据意味着越大计算量、越长计算时间和越高计算功耗。“驭浪者”号本身能够携带的能源有限,为了较少计算功耗,选用低功耗的ARM作为处理芯片。为了减少计算量和计算时长,仿生智能算法被广泛应用于无人艇路径规划场景。

GA算法和PSO算法具有实现简单,计算量小的特点,被广泛地应用于无人艇的路径规划中,张跃星等[27]提出一种基于海图和改进粒子群优化算法的全局路径规划方法,解决AUV在复杂条件海域做全局路径规划时面临的环境信息缺少,环境建模困难和常规算法复杂、求解能力弱等问题。仿真实验结果表明,该方法与传统粒子群算法相比,规划出短航程、安全性高的全局路径的能力更强,可满足AUV在复杂海域航行时的全局路径规划需求。Alvarez等[28]提出一种基于GA算法的路径规划算法,该算法考虑海流对无人艇航行的影响,利用射流函数[29-34]预测随时空变化下的海流数据,保证无人艇在安全到达目标点的同时消耗最少能源。Ma等[35]提出一种DAMOPSO算法,该算法以PSO算法为基础,同样利用射流函数,预测随时空变化的海流数据,考虑无人艇的速度约束,得到能够安全到达目标点、航行时间最短、能源消耗最少的路径。该射流函数尽管可以模拟流场的变化,对算法进行仿真试验验证,但该函数仍是通过分析特定环境下的海岸线数据和海流数据得到的,对于无人艇的实际航行不具有普适性。

从上述研究可以看出,无人艇经典的能源最优路径规划算法如A*算法、Dijstra算法、维诺图算法、可见图算法和水平集算法等均需要规模较大、精度较高的海岸线和海流数据,但是精度较高、规模较大的数据集会造成算法运行时间过长、计算量过大等问题。而过长计算时间会造成路径无法及时更新的问题,在实时变化的海流环境中,无法随海流变化及时更新的路径会使算法失去时效性。

为了解决这一问题,Niu等[36]依靠海流数据集对海流进行预报,通过一次运算得到最优路径,不需要在航行过程中不断地更新路径。PSO算法和GA算法由于本身算法的特点,以及不需要较高精度的海岸线数据的原因,不会造成计算时间长、计算量大的问题,但仍是通过海流数据集对海流进行预测,通过一次运算得到最优路径。可以看出,这些算法的结果会受到海流数据集尺度和海流预报模型的影响。使用的数据集尺度越大,算法的结果越不准确。但是大多数海流数据集能够提供的数据尺度又太大,而在不同的海域,数据集能提供的时间尺度、空间尺度存在显著区别。海流数据模型构建同样受到数据集尺度影响,且无人艇在不同海域航行时,需要建立不同海流模型,对于实船航行不具有普适性。

研究中探索一种基于在线海流数据的自然能驱动无人艇能源最优路径规划算法。该算法保证“驭浪者”号在随时间空间变化的海流环境中,能够安全地到达目标点,同时消耗最少的能源。该算法不需要使用大规模的海流数据集,也不需要在不同海域建立海流预测模型,而是利用在线的海流数据,不断地更新路径,从而解决能源最优的路径规划问题。主要内容由以下4部分组成:

1)考虑“驭浪者”号的回转半径,设计距离最优的路径规划算法(distance optimal particle swarm optimization,DOPSO);

2)分析海流、风对“驭浪者”号能源消耗的影响,设计静态流场下的能源最优路径规划算法(energy optimal particle swarm optimization, EOPSO);

3)根据在线海流数据,在“驭浪者”号航行过程中不断地对路径进行优化,提出基于在线海流数据的能源最优路径规划算法(energy optimal particle swarm optimization based on online current data, OCPSO);

4)设置典型工况,开展OCPSO算法和DOPSO算法的仿真对比试验,验证所提算法的可行性和有效性。

1 距离最优的路径规划算法

1.1 “驭浪者”号自然能驱动无人艇

以“驭浪者”号自然能驱动无人艇为研究对象,如图1所示,主尺度如表1所示。“驭浪者”号搭载了流速计、气象站等环境数据传感器,可以在线监测当前位置的海流、风的方向和速度等信息。

表1 “驭浪者”号的主尺度Table 1 Main dimension of “Wave Rider”

图1 “驭浪者”号自然能驱动无人艇Fig.1 “Wave Rider” natural energy-driven unmanned surface vehicle

通过海上实船回转试验数据,可以得到“驭浪者”号在最大舵角下的最小回转半径为15 m,如图2～3所示。

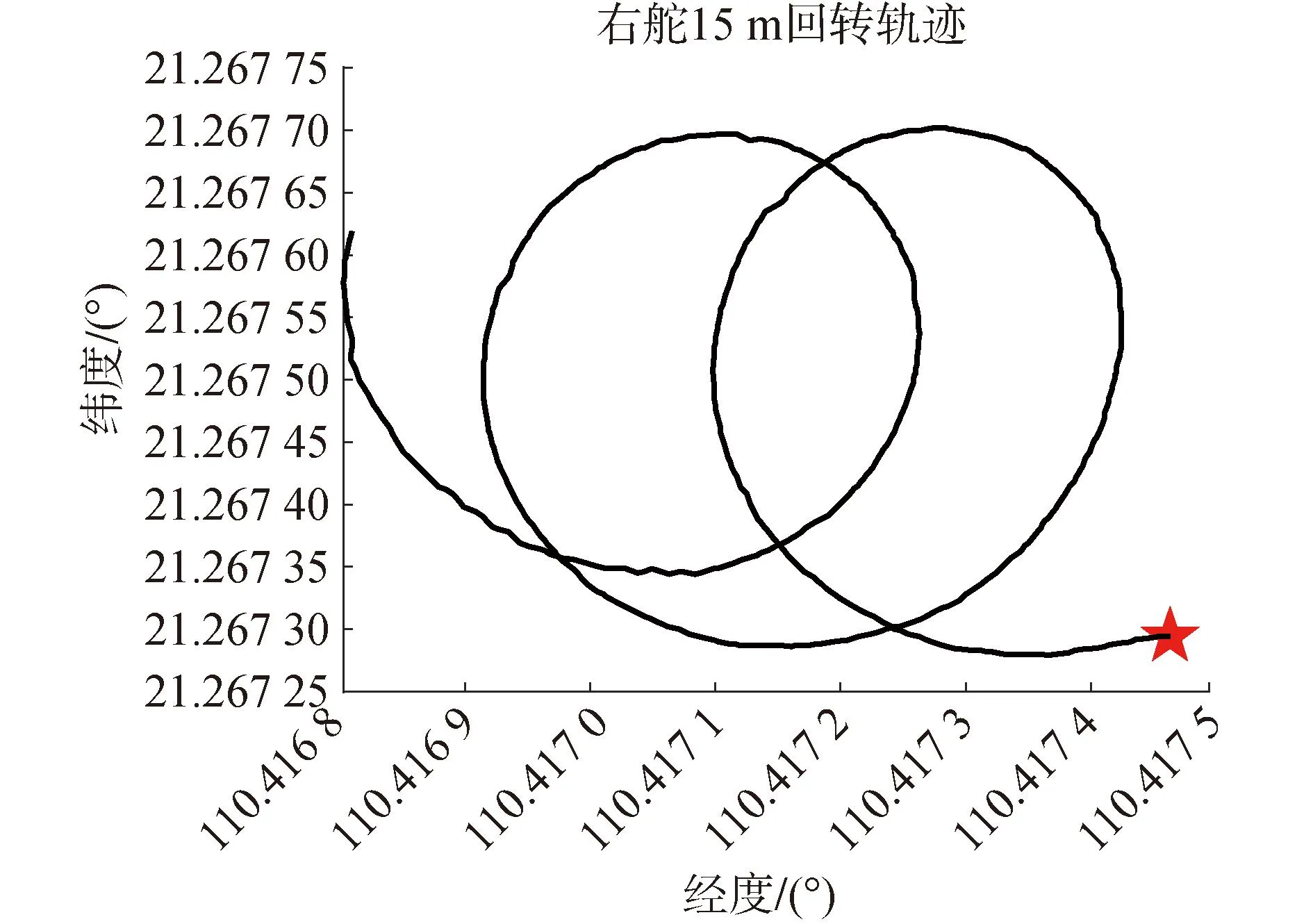
图2 最大右舵的回转轨迹Fig.2 Rotation trajectory of maximum right rudder

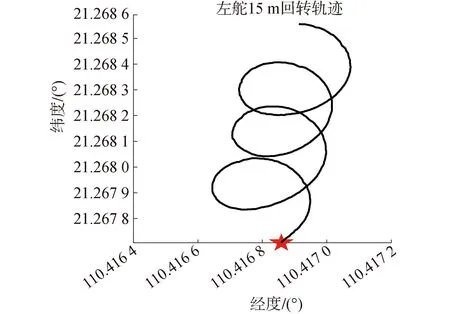
图3 最大左舵的回转轨迹Fig.3 Rotation trajectory of maximum left rudder

“驭浪者”号的推力来自于一个电力推进器,该型电力推进器推力的敞水试验结果如图4所示,功率的敞水试验结果如图5所示。

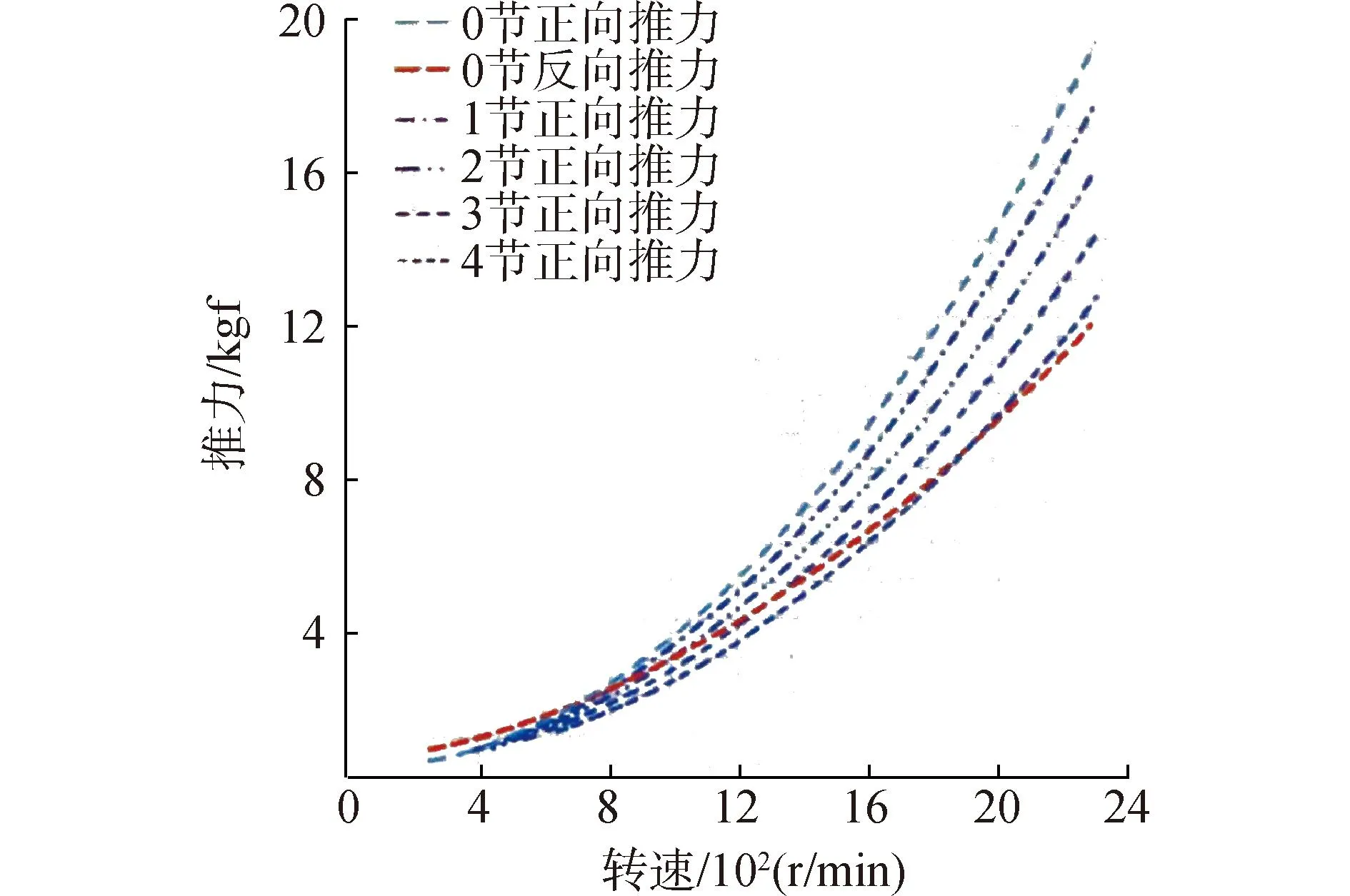
图4 推力敞水试验Fig.4 Thrust open water test

图5 功率敞水试验Fig.5 Power open water test

1.2 坐标系的构建

为了便于说明算法运行机理和算法验证提供基础,本文构建了基础坐标系,设置障碍物环境,介绍以距离最优为目标的路径规划算法(DOPSO)。该算法以PSO算法为基础,结合“驭浪者”号的回转半径,得到其能够安全地从起始点到达目标点的最短路径。

研究中采用极坐标作为基础坐标系,以航行的起始点作为极坐标系的原点,以起始点到目标点的射线作为极坐标系的极轴。将不规则障碍物的最大长度加上预设的安全距离作为障碍圆的直径。为了研究方便,在极坐标系极轴两侧设置3个障碍圆,如图6所示。

图6 极坐标系Fig.6 System of polar coordinates

通常,PSO算法在运行前需要确定粒子的维度,研究中引入维度圆的概念[34-35],如图2所示,以起始点为圆心,起始点到障碍物圆圆心的距离为半径构建维度圆,半径最小的维度圆为第1维度圆D1,其次是第2维度圆D2,半径最大的为第3维度圆D3,每个维度圆上有且仅有一个路径点(xi,yi),i=1,2,3,4,粒子的维度由起始点S(x0,y0)、路径点(xi,yi)、目标G(x0,y0)的极角构成:

X=[ρs,ρ1,ρ2,ρ3,ρg]

(1)

式中:X为粒子位置;ρs为起始点的极角;ρg为目标点的极角;ρ1、ρ2、ρ3为维度圆上路径点的极角;ρs、ρg均为0。

1.3 算法的说明

为了安全有效地避开航行路径上的障碍物,需要计算各维度圆上路径点的禁入角。假设维度圆D1上的路径点P1已知,需要计算维度圆D2上路径点P2的禁入角,D2上的禁入角由弧度T1和弧度T2组成,如图7所示。

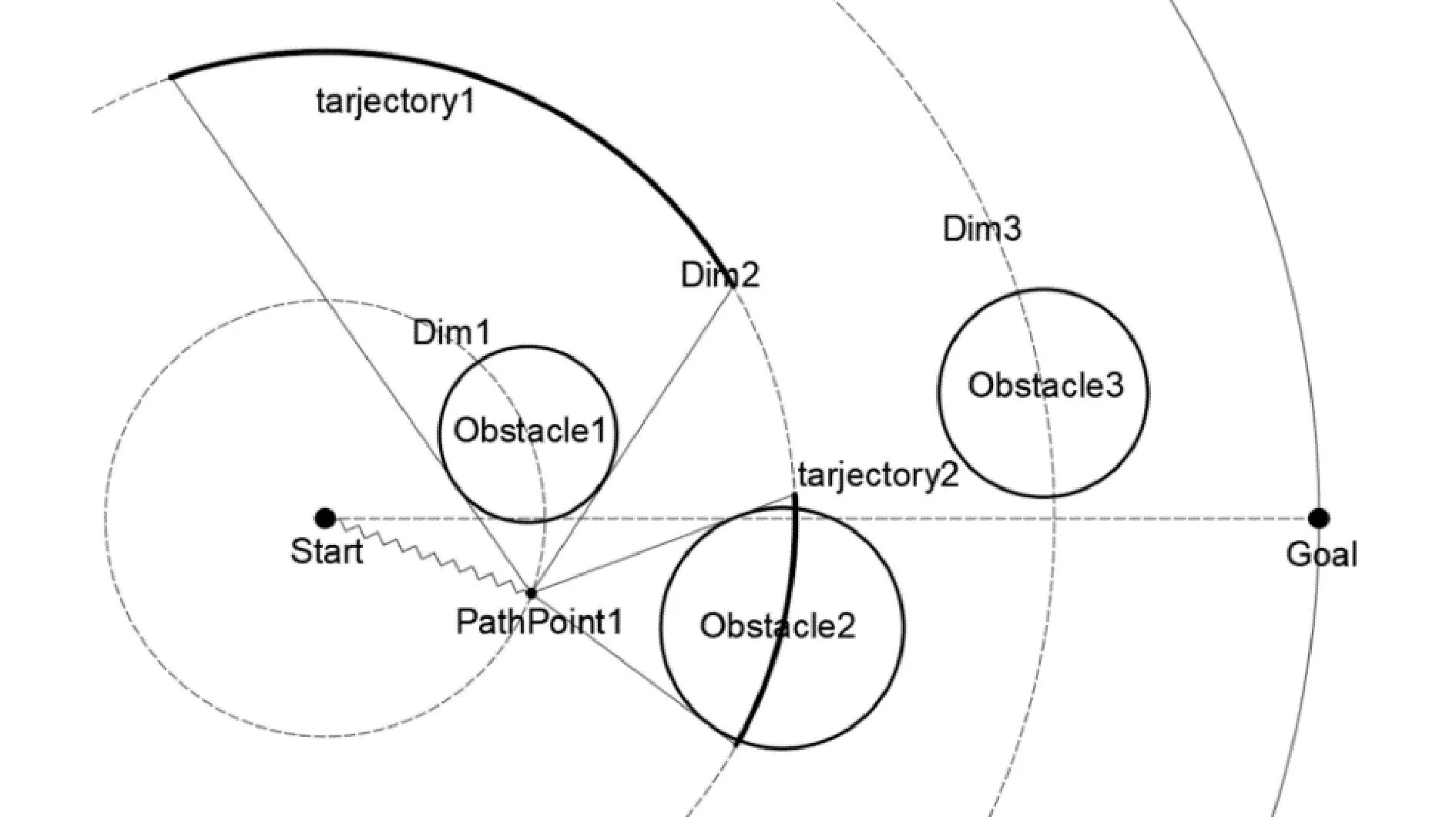
图7 计算禁入角Fig.7 Calculate forbidden angle

为了使规划出的路径具有可行性,同时以最短的路径到达目标点,算法需要考虑“驭浪者”号最小回转半径的影响,以距离最优为目标,对路径进行优化,得到距离最优的路径规划算法(DOPSO)。如图6所示,路径Path是从起始点到目标点的最短路径,其从起始点到目标点的航行距离可以表示为L0,即为粒子的适应度:

(2)

但是,考虑到最小回转半径和禁入角的影响,需要进入惩罚函数对粒子进行优化,若粒子不满足最小回转半径和禁入角的约束,则该粒子的适应度值取正无穷。DOPSO的流程如图8所示。

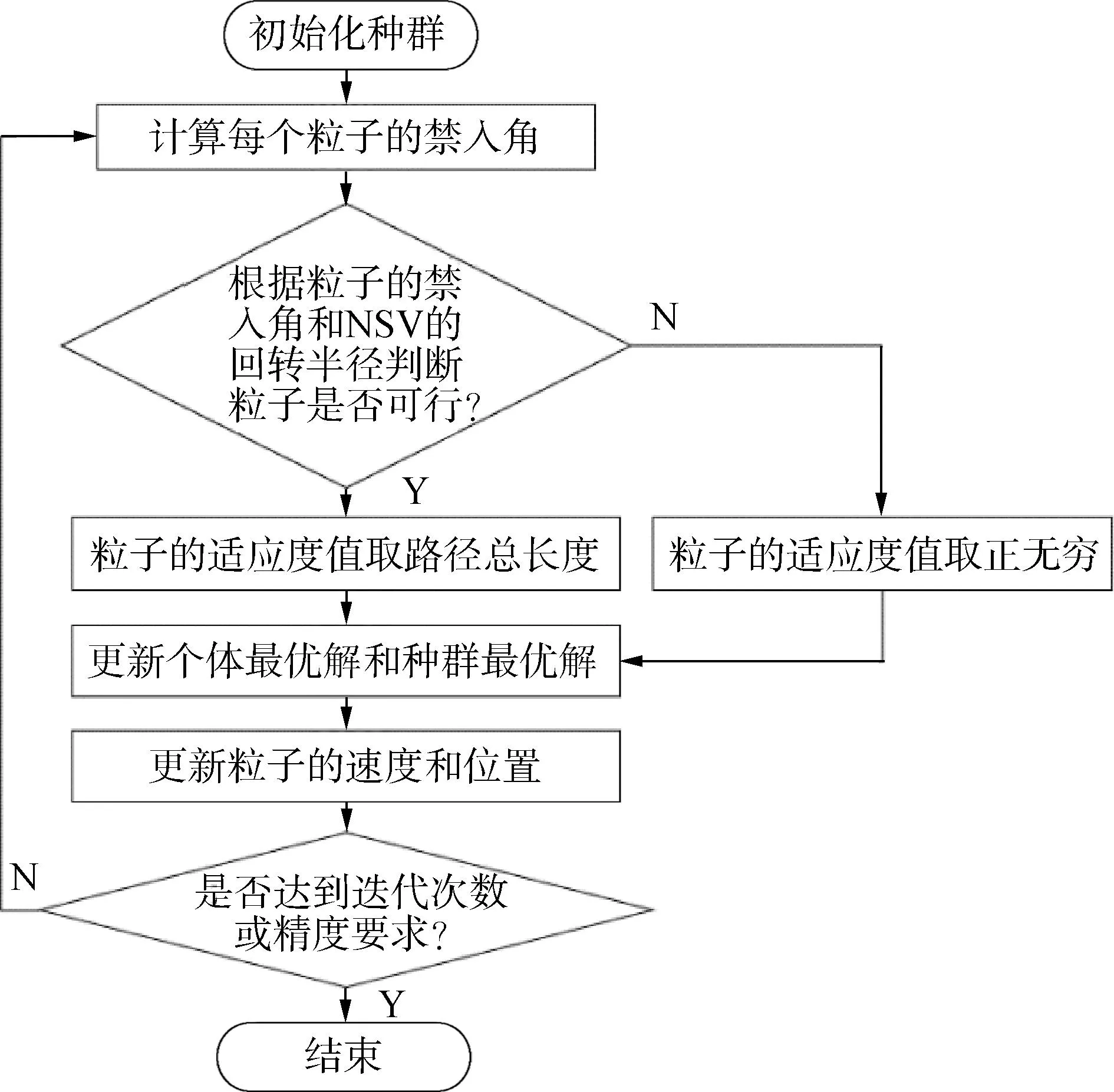
图8 DOPSO算法流程Fig.8 DOPSO algorithm flow chart

2 基于在线海流数据的能源最优路径规划算法

2.1 能源消耗模型的构建

为了实现能源最优的路径规划算法,需要分析“驭浪者”号能源消耗的主要来源。“驭浪者”的推进方式为单螺旋桨的电力推进,阻力主要来自于风和流,而航行过程中的能源消耗主要来自于克服海流阻力和风阻力做的功,“驭浪者”搭载的传感器能够搜集到航行过程中的能源消耗和海流、风的在线数据。

为了进行能源最优路径规划研究,首先需要得到海流和风对“驭浪者”产生的阻力公式。由于“驭浪者”尺寸较小,对于海流阻力,只考虑表层水平流阻力,假设海流定常且均匀,海流阻力可分为摩擦阻力和剩余阻力,其中剩余阻力包括粘压阻力和兴波阻力。因此,海流产生的总阻力可以表示为:

(3)

式中:Rf为摩擦阻力;Rw为粘压阻力;Rpv为粘压阻力;CT为总阻力系数;ρw为海水密度;Swet为艇体湿表面积;V为“驭浪者”号相对海流的速度。

根据式(3)计算“驭浪者”号所受的海流阻力为:

(4)

式中:Fc为“驭浪者”号所受海流阻力;ψrc为“驭浪者”号的航速和海流流向的夹角;Uc为海流速度;us为“驭浪者”号航速的大小。

由于“驭浪者”号的上层建筑表面积较大,且具有风机等风能驱动设备,风力对“驭浪者”号的阻力影响比较大,根据伯努利方程可以得出单位受风面积的风压力为:

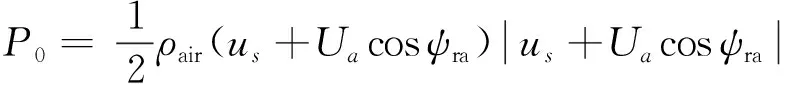
(5)

式中:P0为基本风压力;ρair为空气密度;ψra为风的风向和“驭浪者”号航向的夹角;Ua为海平面风速;us为“驭浪者”号航速的大小。

令式(5)中空气密度ρair取1.293 kg/m2,则基本风压力可以表示为:

P0=0.646 5(us+Uacosψra)|us+Uacosψra|

(6)

根据基本风压力P0可以求得一定横截面积上所受风阻力的大小,因此“驭浪者”号所受平均风阻力可以表示为:

|us+Uacosψra|CA

(7)

式中:C为风压力系数;A为“驭浪者”号水线以上正投影面积。

根据前期的计算流体力学分析、船舶三维模型计算和实船测算,可以得到“驭浪者”号的湿表面积Swet、水线以上正投影面积A。根据实船直航实验,可以得到总阻力系数CT、风压力系数C,代入式(4)和式(7),得到:

Fc=3.9(us-Uccosψrc)|us-Uccosψrc|

(8)

Fw=0.02(us+Uacosψra)|us+Uacosψra|

(9)

为了减少频繁切换推进器转速造成的功率损耗和推进器磨损,设置“驭浪者”号在航行过程中,推进器始终保持最大转速2 000 r/min。得到推进器推力公式和功率公式为:

Ft=0.007 6(us-Uccosψrc)2-

2.654(us-Uccosψrc)+17.024

(10)

Pt=-39.5(us-Uccosψrc)+850

(11)

式中:Ft为推进器推力;Pt为推进器功率。

在“驭浪者”号的航行过程中,推力和阻力的关系为:

Ft=Fc+Fw

(12)

2.2 静态海流环境下的能源最优路径规划算法

假设“驭浪者”号航行在静态海洋环境中,因此起始时刻传感器监测到的海流和风数据,可以代表全局的海流和风数据。EOPSO算法得到在静态环境下能源最优路径Path,如图9所示。

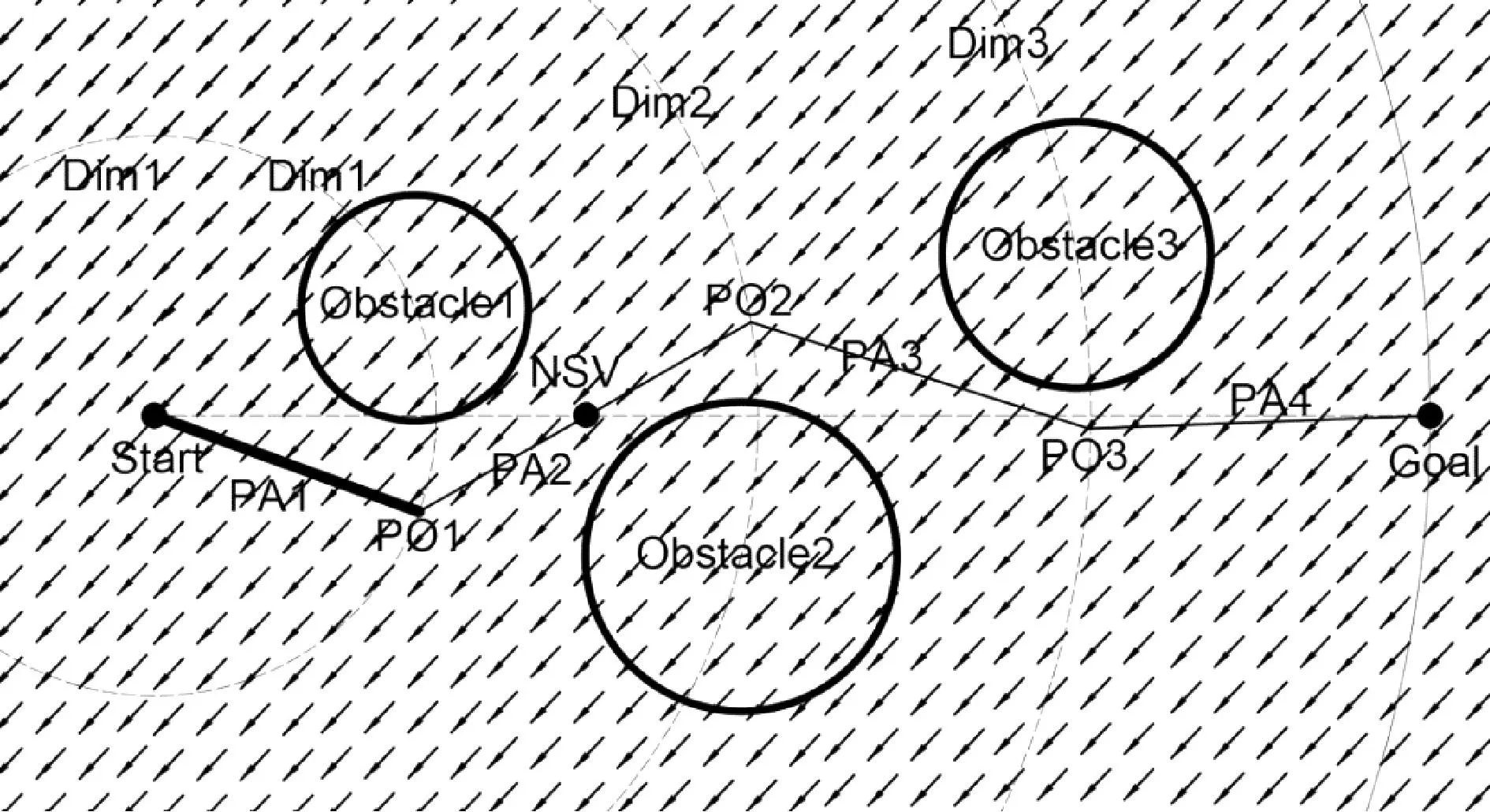
注:箭头代表海流方向。图9 EOPSO算法Fig.9 EOPSO algorithm

根据海流和风的数据以及式(4)、(7)、(10)、(12)可以得到不同位置的航行速度us(xi,yi)。再根据式(11)得到不同航行位置的推进器功率Pt(xi,yi),通过对功率的积分得到“驭浪者”号航行完该路径消耗的总功,即总的能源消耗。由于静态海流环境下海流和风不会发生变化,“驭浪者”号在每一段路径PAi(i=1,2,3,4)的速度均相同,可以表示为ui,i=1,2,3,4,路径长度可以表示为Li,i=1,2,3,4,功率可以表示为Pi,i=1,2,3,4,W可以表示为:

(13)

式中:W为“驭浪者”号航行完整路径消耗的总能源消耗量。根据W对PSO算法的适应度函数进行改进,得到静态海流环境下能源最优的路径规划算法(EOPSO)。

2.3 基于在线海流数据的能源最优路径规划算法

在“驭浪者”号实际航行过程中,海流、风的大小和方向可能会产生较大变化,此时若仍是按照起始时刻得到的路径去航行,可能消耗更多的能源。因此,在航行过程中需要根据在线的海流和风数据,以及“驭浪者”号产生的能源消耗,不断地对路径进行优化,保证在安全到达目标点的同时,消耗最少的能源。此外,任何路径规划算法都会消耗一定的计算时间,在航行过程中,路径更新同时也要考虑算法运行时间的影响,避免对正常航行产生影响。探索基于在线海流数据的能源最优路径规划算法,路径的更新过程如下:

输入:起始点S(x0,y0),目标点G(x4,y4),障碍圆的圆心坐标(xobs1,yobs1),(xobs2,yobs2),(xobs3,yobs3), 障碍物的半径R1,R2,R3,起始时刻监测到的海流速度Uc,风速Ua。

输出:路径点PO1(x1,y1),PO2(x2,y2),PO3(x3,y3)与总的能源消耗W。

1) 根据起始时刻的Uc和Ua,运行EOPSO算法,得到能源最优的路径P1;

2) “驭浪者”号开始时刻记为T0,沿规划出的路径PA1航行,目标路径点为PO1,航行过程中不断地监测Uc和Ua的变化情况;

3) 在Ti时刻,监测到Uc发生了剧烈的变化, 记录Ti(i>0)时刻的目标路径点POi,i=1,2,3,4;

4) 保持任一粒子前i维的极角ρs,…,ρi不变,根据Ti时刻的Uc和Ua,以及“驭浪者”从T0到Ti时刻产生的能源消耗Wpasti,运行EOPSO,在Ti+1时刻得到新的路径Pi(i>1)。

5) 若Ti+1时刻的目标路径点仍为Pi,则更新路径为Pi(i>1),若不是,则重复步骤3)、4);

6) 判断“驭浪者”是否到达目标点G(x4,y4),若是,则停止程序,记录传感器监测到的能源总消耗W;若不是,则运行步骤7);

7) 监测Uc和Ua的是否产生了剧烈变化,若是,则运行步骤3);若不是,运行步骤6);

对于步骤3)和4)的说明:假设“驭浪者”号从起始时刻T0航行到T1时刻,传感器监测到的海流变化不大,不用更新路径,“驭浪者”沿路径P1航行。在T1时刻,“驭浪者”号的位置为(xNSV1,yNSV1),目标路径点是P2,从T0到Ti时刻产生的能源消耗为Wpast1,(xNSV1,yNSV1)到P2的距离为L2,如图10所示。

图10 T0到T1时刻的航行路径Fig.10 Sailing path from T0 to T1

在T1时刻监测到海流产生了较大变化,此时海流和风的速度为Uc和Ua,保持粒子第1维、第2维的极角ρ1,ρ2不变,根据Uc、Ua及式(4)、式(7)、式(10)、式(12)可以得到新的ui、Li、Pi,i=2,3,4,W表示为:

(14)

重新计算能源最优路径,在T2时刻,“驭浪者”位置为(xNSV2,yNSV2),得到新的能源最优路径P2。同时,利用式(14)计算P1在当前的Uc和Ua下能源消耗Wpast。若Wpast>W且T2时刻目标路径点仍是PO2,则更新路径,如图11所示。

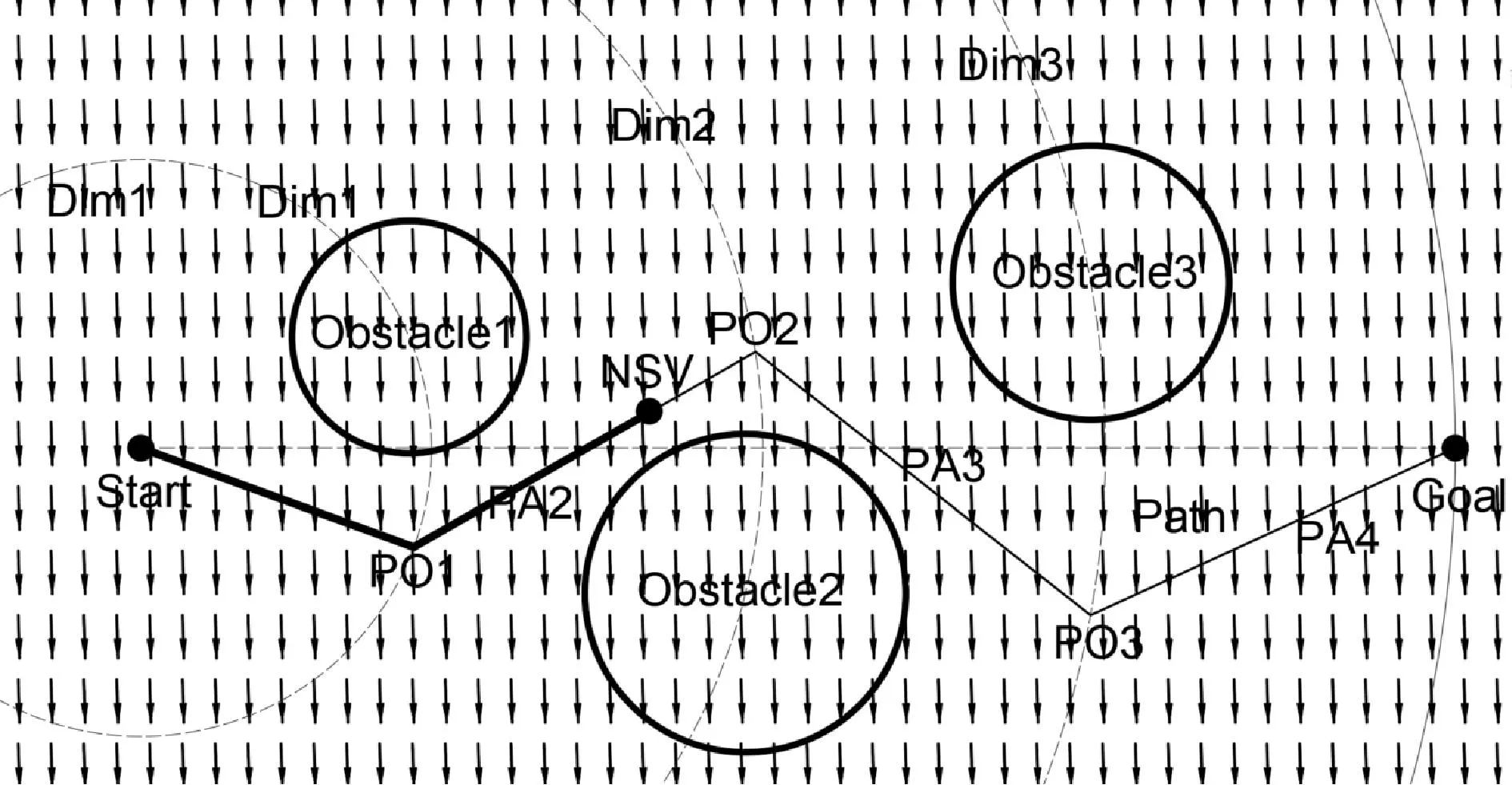
图11 T2时刻的航行路径Fig.11 Sailing path in T2

3 仿真对比试验与分析

为了验证算法的可行性和有效性,研究中设置在中国广东湛江海域内进行仿真实验,起始点的经纬度为(110.421 910 ,21.263 390 ),目标点的经纬度为(110.422 070 ,21.260 650 ),障碍物由3组静态障碍物组成,圆形虚线表示障碍物的范围,如图12所示。起始时刻,风向正东、速度7 m/s;海流流速1.2 m/s,流向如图12中箭头所示。起始时刻距离最优路径规划算法(DOPSO)得出的路径由黑色线条表示,能耗最优路径规划算法(EOPSO)得出的路径由灰色线条表示;黑色、灰色方块代表路径的航行节点。

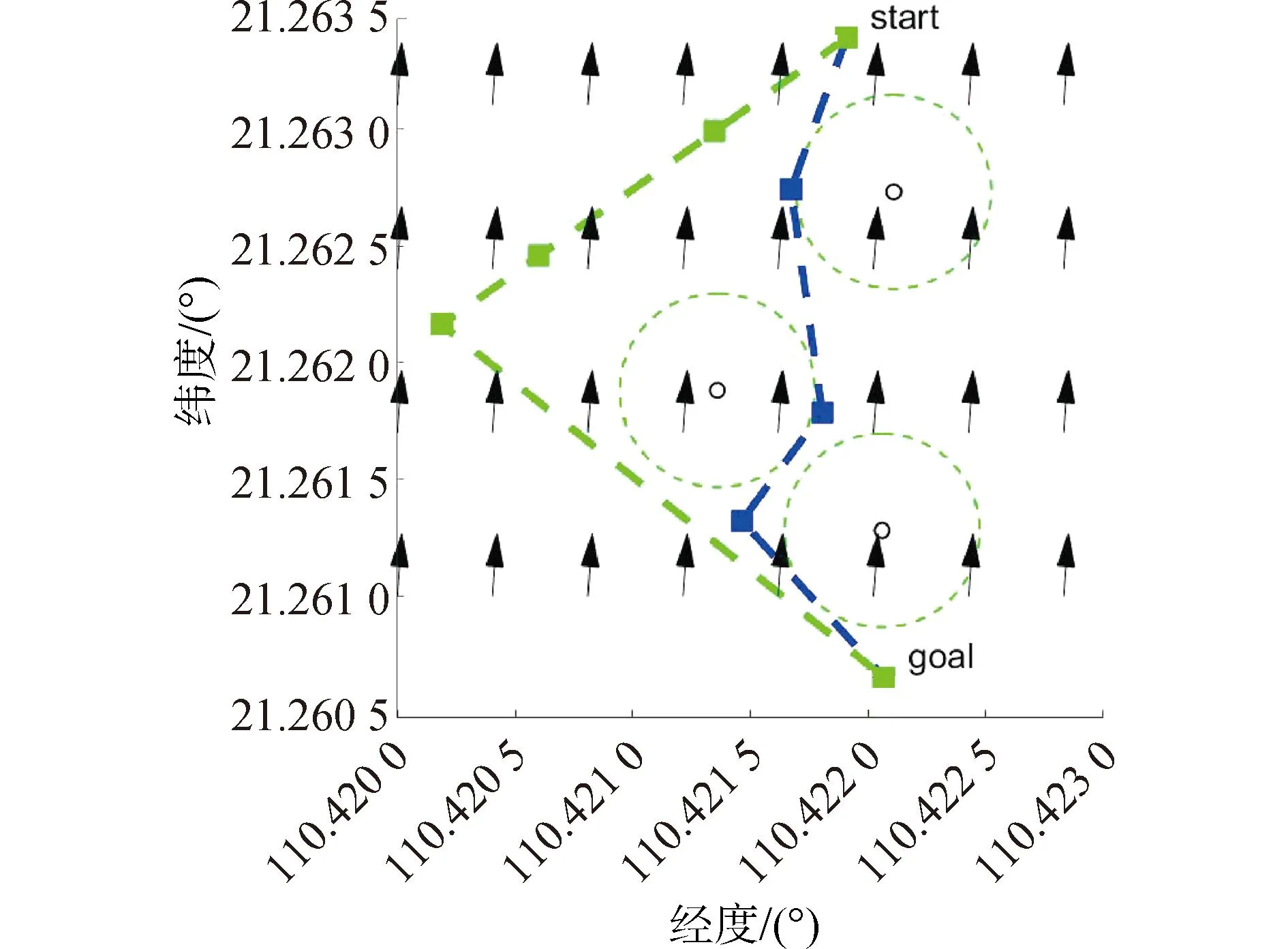
图12 起始时刻的路径Fig.12 Path in the beginning

DOPSO算法和EOPSO算法得到的路径点的坐标、路径预测能源消耗值和路径长度如表2所示,其中,(x0,y0)代表起始点的经纬度,(x1,y1)、(x2,y2)、(x3,y3)代表路径点的经纬度,(x4,y4)代表目标点的经纬度。

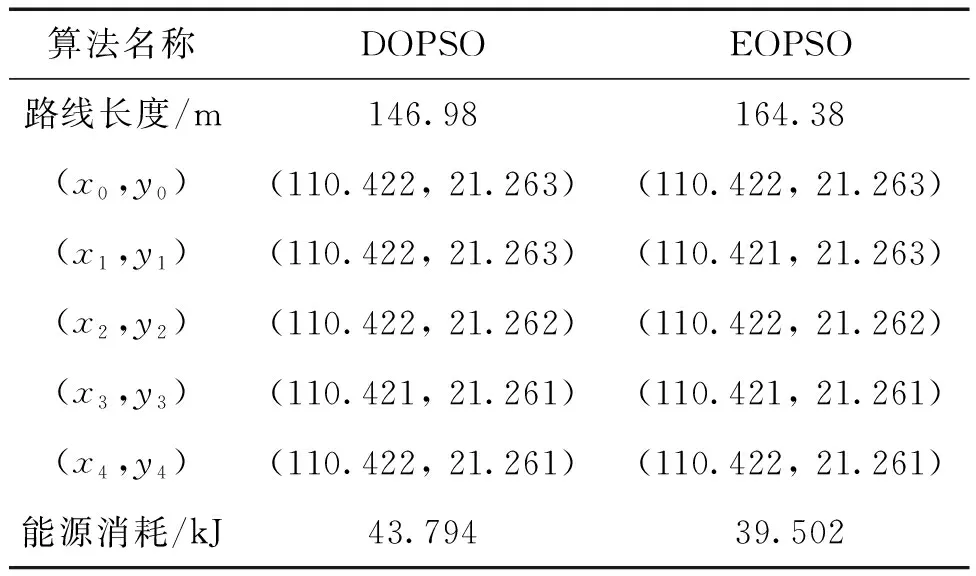
表2 起始时刻的路径表Table 2 Path table in the beginning

设置“驭浪者”号在航行到第8 min时,海流的方向发生了较大的变化,需要更新路径。此时海流的方向为如图13的箭头所示。根据当前时刻监测到的海流的大小和方向,OCPSO算法得出新的路径,OCPSO算法得到的路径由实线条表示,方块代表OCPSO算法得到的路径上的路径点,“驭浪者”号前8 min航行的轨迹由粗实线表示,如图13所示。

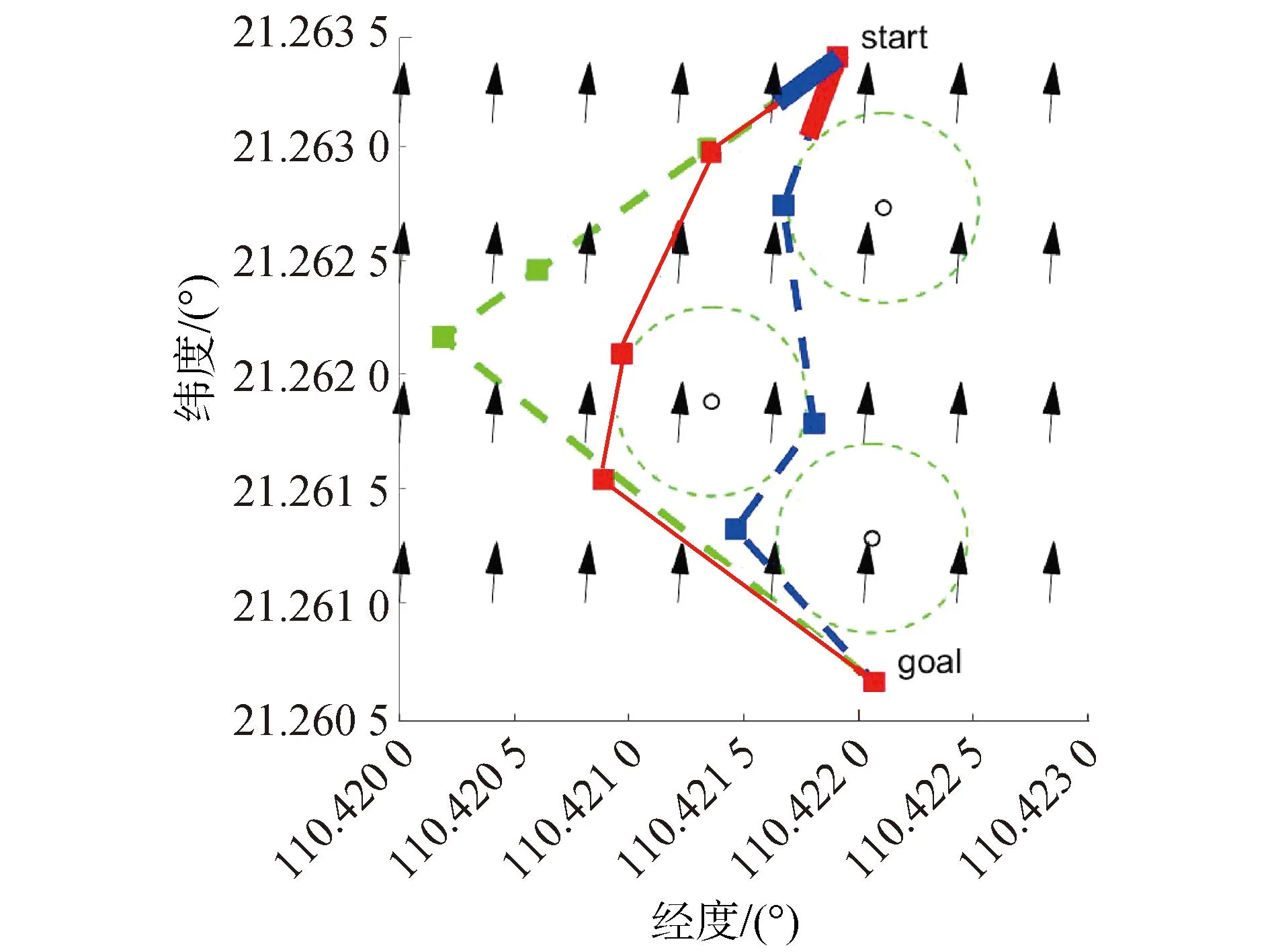
图13 第8分钟的路径Fig.13 Path in the 8th minute

第8 min时,DOPSO算法和OCPSO算法得到的路径点坐标、前8 min的能源实际消耗值、总能源消耗预测值和路径长度,如表3所示。

表3 第8分钟时的路径表Table 3 Path table in the 8th minute

设置“驭浪者”号在航行到第32 min时,海流的方向发生了变化,此时海流的方向如图14的箭头所示,“驭浪者”号前32 min航行的轨迹由粗实线表示。根据当前时刻的监测到的海流大小和方向,OCPSO算法没有得出新的路径,但是能源消耗的预测值产生了很大的变化,如图14所示。

图14 第32分钟的路径Fig.14 Path in the 32th minute

第32分钟时,DOPSO算法和OCPSO算法得到的路径点坐标、前8分钟的能源实际消耗值、前32分钟的能源实际消耗值、总能源消耗预测值和路径长度,如表4所示。

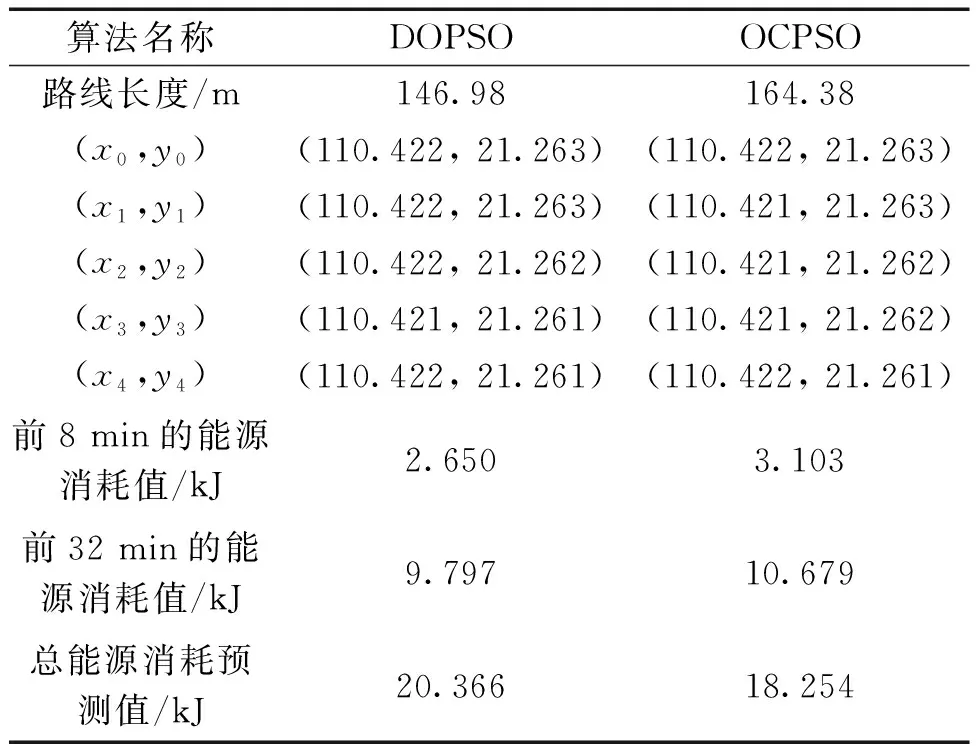
表4 第32分钟时的路径表Table 4 Path table in the 32th minute

在航行到目标点时,DOPSO算法和OCPSO算法的总能源消耗实际值和表4中总能源消耗预测值一致。根据仿真对比试验结果,“驭浪者”号从起始点到目标点,OCPSO算法得到的路径比DOPSO算法得到的路径,节约了10.37%的能源。

4 结论

1)通过实验得到“驭浪者”号的最大回转半径,并结合推进器推力、功率敞水试验数据,分析得到禁入角,以距离最优为目标对路径进行优化,基于粒子群算法设计了距离最优的路径规划算法(DOPSO)。

2)分析海流和风对“驭浪者”号能源消耗的影响,建立能源消耗模型;根据能源消耗模型,设计了静态流场环境下能源最优路径规划算法(EOPSO)。基于在线海流数据,不断地对路径进行优化,提出了基于在线海流数据的能源最优路径规划算法(OCPSO)。实现变化的海流环境下,安全到达目标点时,搜索到消耗最少能源的路径。

3)开展了典型场景下,距离最优路径规划算法(EOPSO)和基于在线海流数据的能源最优路径规划算法(OCPSO)的仿真对比实验研究,试验验证了在线海流数据能源最优路径规划算法比距离最优路径规划算法,可实现节约10.37%的能源。

未来的研究中,将重点探索风、光、波、流等多能源形式耦合影响下,自然能驱动无人艇的能源最优路径规划方法;同时,开展实艇的外场试验研究,进一步促进自然能驱动无人艇的续航能力提升和相关技术发展。