基于航迹规划的无人机地形辅助导航

张睿, 李万睿, 肖勇, 杨林, 许斌

(1.东南大学 自动化学院, 江苏 南京 210096; 2.西北工业大学 自动化学院, 陕西 西安 710072; 3.成都飞机设计研究所, 四川 成都 610041)

地形辅助导航(terrain-aided navigation, TAN)是近年来受到广泛重视并已成功使用的辅助导航技术[1]。地形轮廓匹配(terrain contour matching, TERCOM)具有完全自主、导航误差不随时间积累的优点,它利用飞行路径正下方的地形高度和存储的参考高程地图进行比较,进而得出飞行器的位置信息。目前TERCOM可以达到百米以内的定位精度,使用TERCOM技术可以提高无人机(unmanned aerial vehicle,UAV)组合导航系统的系性能和可靠性,提高战机低空突防能力。

随着国内外学者的广泛研究,在传统TERCOM的基础上已演变出了基于最近等值点迭代法[2]和基于滤波技术的桑迪亚惯性地形辅助导航[3]等多种匹配方法。但是基于高程的地形匹配普遍面临着受匹配精度受地形起伏程度影响较大的问题。针对上述问题,文献[4-5]提出了二维图像与地形高程相结合的匹配方式,以减弱地形辅助导航对地形高程变化的依赖。文献[6]提出了一种基于粒子滤波和长短时记忆网络相结合的TAN算法,来降低飞行器在平坦地形上的导航误差。采用传统平均平方差算法(mean square difference, MSD)、平均绝对差算法(mean absolute difference, MAD)和交叉相关算法(cross correlation, COR)匹配算子的TERCOM算法,存在耗时长实时性差的问题[7]。经大量研究证实[8-10],采用智能优化算法代替传统地形匹配中的遍历算法能够保证搜索最佳匹配位置,并且提高搜索匹配的效率。粒子群优化算法(particle swarm optimization, PSO)作为智能群优化方法的典型代表[11],具有结构简单、状态更新容易实现且没有许多需要调节的参数的优点,广泛应用于各类优化问题中,近年来也应用于地形匹配中[12]。但是在实际应用过程中,粒子群优化算法存在早熟收敛的问题,容易陷入局部极值点,从而导致不能收敛到全局极值点,为了提升粒子群算法的寻优性能,本文在PSO基础上引入分布估计(estimation of distribution algorithm, EDA)的思想,加强PSO算法的全局寻优能力,形成了分布估计思想的优化PSO算法。

本文研究基于航迹规划的地形辅助导航算法。首先采用A*算法进行航迹规划,为飞行器规划出途经地形起伏较大区域的航路,其次采用优化PSO算法进行地形匹配,改善传统TERCOM实时性差的问题,最后进行惯性导航/地形匹配组合导航。

1 基于A*算法的地形辅助导航航迹规划

TERCOM算法对地形的依赖性较强,所以匹配区域的地形适配性是否满足算法的要求就显得至关重要。本文采用航迹规划选出始终在地形起伏明显区域的飞行航迹,再利用地形辅助导航算法提升导航精度,其工作流程如图1所示。

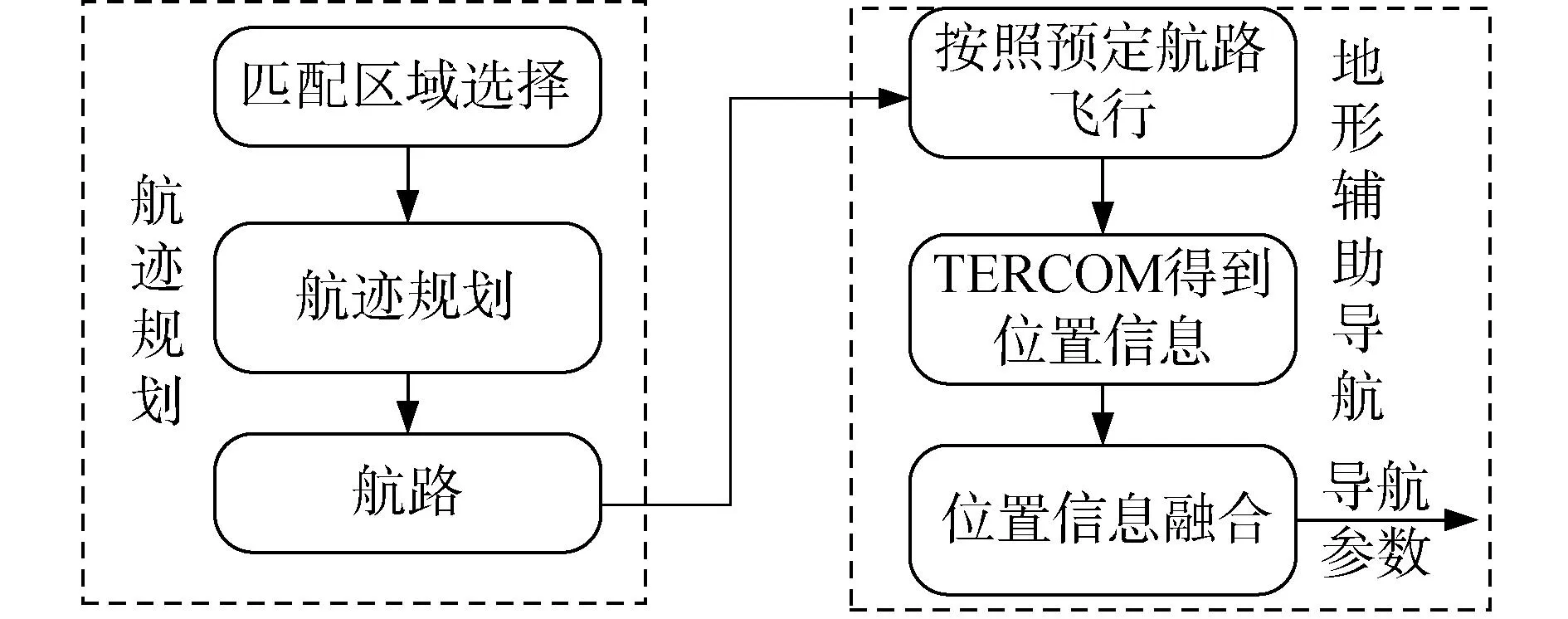
图1 基于航迹规划的地形辅助导航算法原理Fig.1 Principle of terrain aided navigation algorithm Based on track planning

基于A*算法的地形辅助导航航迹规划的原理为:首先对无人机需要途径的区域进行分块并计算各块地形标准差,根据地形标准差选出地形平坦区域和地形起伏区域,将地形平坦区域视为航迹规划中的威胁区域,避免驶入;其次,在航迹规划时引入地形信息,利用A*算法在地形特征约束下进行离线航迹规划。

基于A*算法的地形辅助导航航迹规划步骤为:

1)获取无人机任务区间数字地图,如图2。

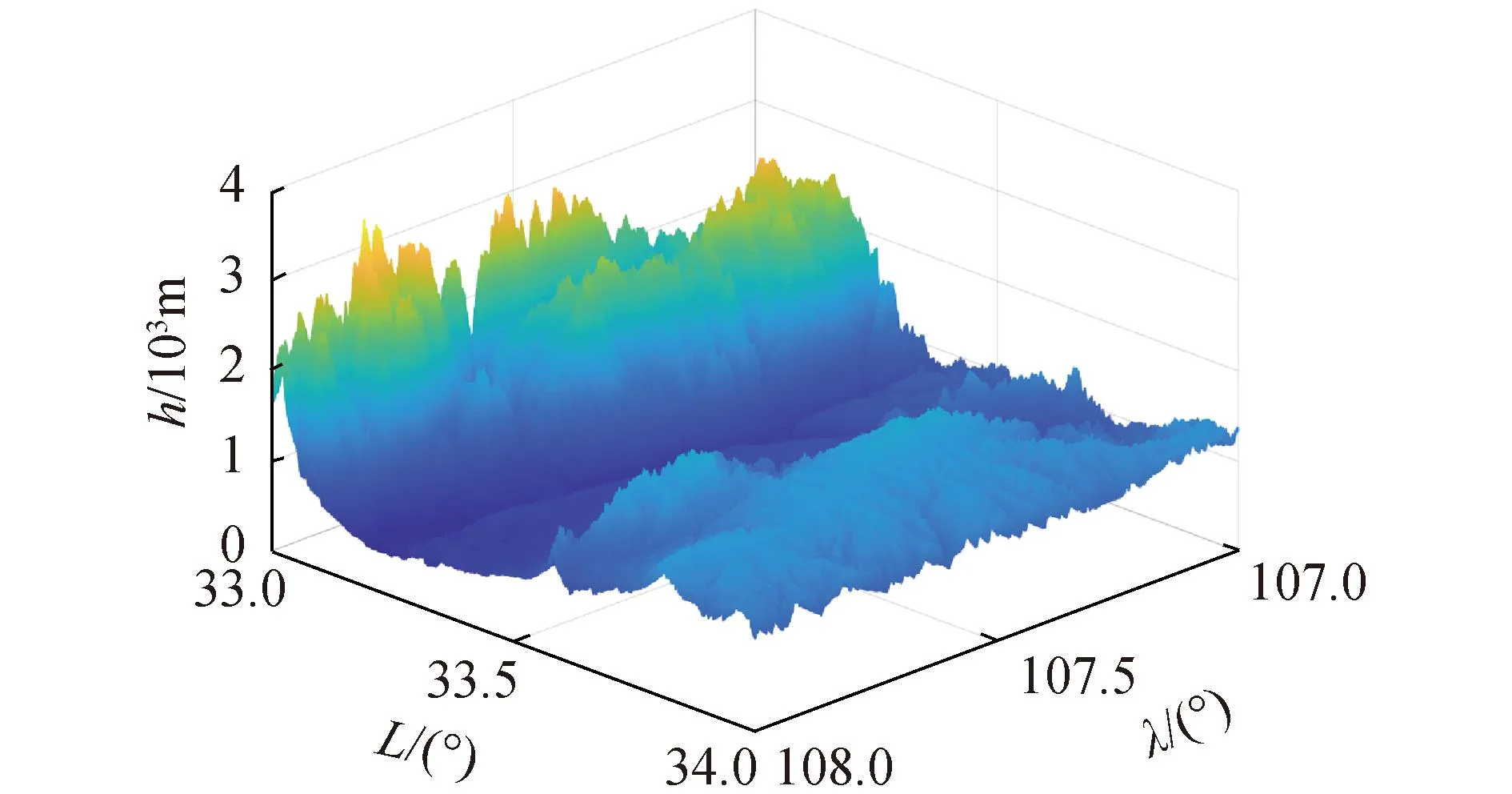
图2 任务区间三维地形图Fig.2 3D topographic map of mission area

2)计算地形标准差。地形标准差通常用来描述地形的总体起伏程度,为保证地形标准差对地形有较强的分级能力,将数字地图分为1 km×1 km的网格,并计算各分块区域内的地形标准差,地形标准差表示为[13]:

(1)

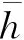
3)划分地形适配区。当地形标准差值大于18时,该区域地形起伏较大[14],可进行地形匹配,故将地形标准差值大于18的区域划分为地形适配区,如图3所示。

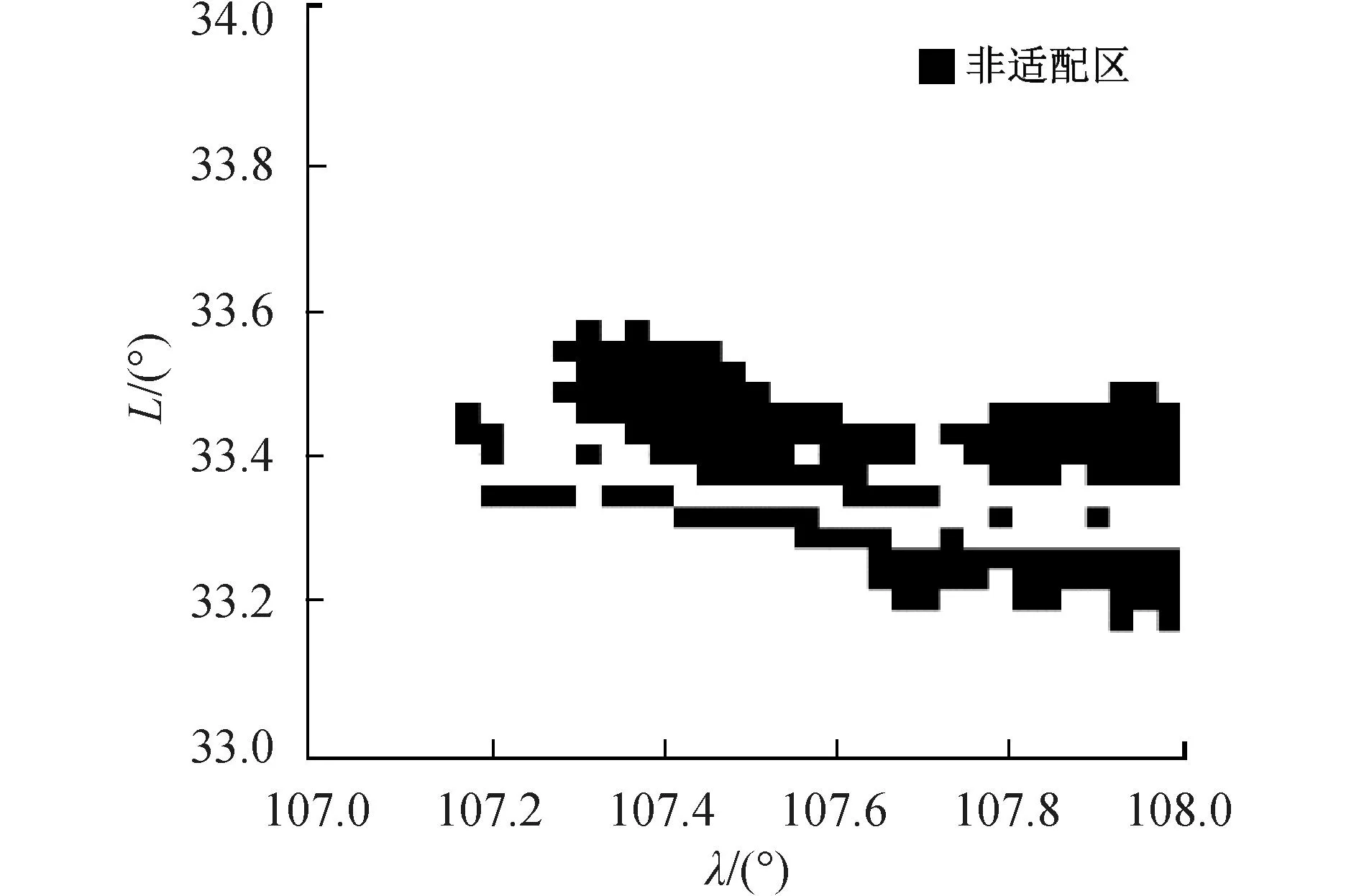
图3 地形平坦区域划分Fig.3 Division of flat terrain

4)采用A*算法进行航迹规划,使无人机尽可能地飞行在地形适配区内。A*算法的航迹代价函数为[15]:

f(x)=g(x)+u(x)

(2)

式中:x为当前节点;g(x)为当前节点到起点的真实路径长度;u(x)为当前节点到目标位置的路径长度估值;f(x)代表从航迹规划初始点经过点x到达目标点的最小航迹长度估计值。

2 基于优化PSO算法的TERCOM方法

传统TERCOM算法采用遍历搜索方式进行实时高程与基准子图间的匹配,当捷联惯导系统(strapdown inertial navigation system,SINS)位置误差积累较大时,基准子图的搜索范围增大,此时的搜索效率较低。本文采用优化粒子群算法代替传统TERCOM中的遍历方法,以提升TERCOM的搜索效率。

在优化粒子群算法中,粒子通过PSO算法与EDA算法交替更新,由于EDA中的种群是根据基准子图的适应度值由最优到最劣排序的,所以PSO-EDA组合方法可以避免搜索方向向局部最优快速收敛。优化PSO算法可以替代传统TERCOM中遍历搜索部分,采用优化PSO算法TERCOM的步骤为:

1)实时高程采集。在匹配时,为了避免速度变化引起实测高程序列与数字地图网格不匹配,通常将SINS的轨迹进行等间距采样,即当UAV飞过一个地图网格的间距时,保存高程值为一个采样点[16]。

2)初始化粒子。在以惯性导航指示位置为中心,±3σ的范围构建搜索区域,在搜索区域内以实测地形高程序列为模板所形成的地形高程序列即为一条基准子图,在使用优化PSO算法搜索时,每条基准子图即为一个粒子,如图4所示。

图4 粒子的表示方法Fig.4 Representation of particles

3)计算粒子适应度值。采用平均方差算法(mean square difference, MSD)计算粒子的适应度值,MSD的计算为[7]:

(3)

式中:N为高度序列的个数;xi为地形剖面中的第i个高程值;yi为实测高程序列中第i个高程值。TERCOM匹配的过程就是找到JMSD最小值的过程。

4)采用EDA算法更新种群。在TERCOM中,基准子图的位置分布服从二维高斯分布[17],即:

(4)

式中xture、yture为飞行器真实位置的经度和纬度。

用适应度最优粒子的位置分布更新二维高斯分布模型中的均值与方差,并根据更新后的模型采样生成新的种群。

5)重新计算粒子适应度值。计算新种群内每个粒子的适应度值。

6)采用PSO算法个体最优值与全局最优值。对每个粒子,将它当前适应度值分别和个体最优适应度值、全局最优适应度值相比较,如果适应度值较小,则对当前个体最优位置和全局最优位置进行更新,粒子的速度和位置更新公式为[11]:

(5)

7)判断终止条件。若未到达最大迭代次数,根据式(2)进行粒子的位置和速度更新,返回步骤2)进行下一次迭代。

8)输出定位结果。输出全局最优值粒子所对应的最佳匹配位置。

综上所述,基于改进粒子群的地形匹配方法搜索流程如图5所示。

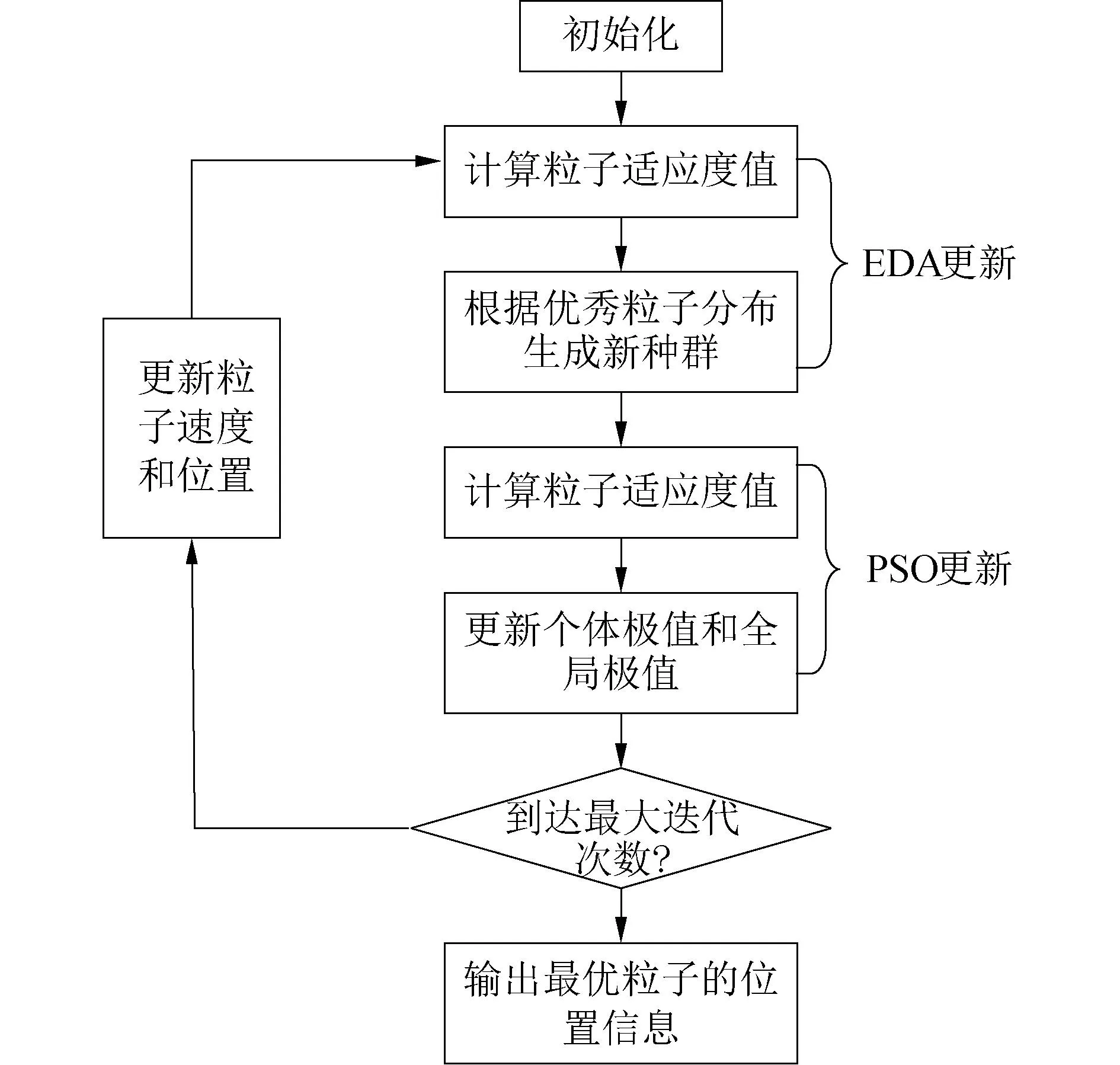
图5 优化PSO更新步骤Fig.5 Optimize PSO update steps

3 惯性/地形组合导航

UAV的惯性导航系统与地形匹配导航系统具有优势互补的特点,将两者组合可以克服各自的缺点,取长补短。组合系统结构框图如图6所示。

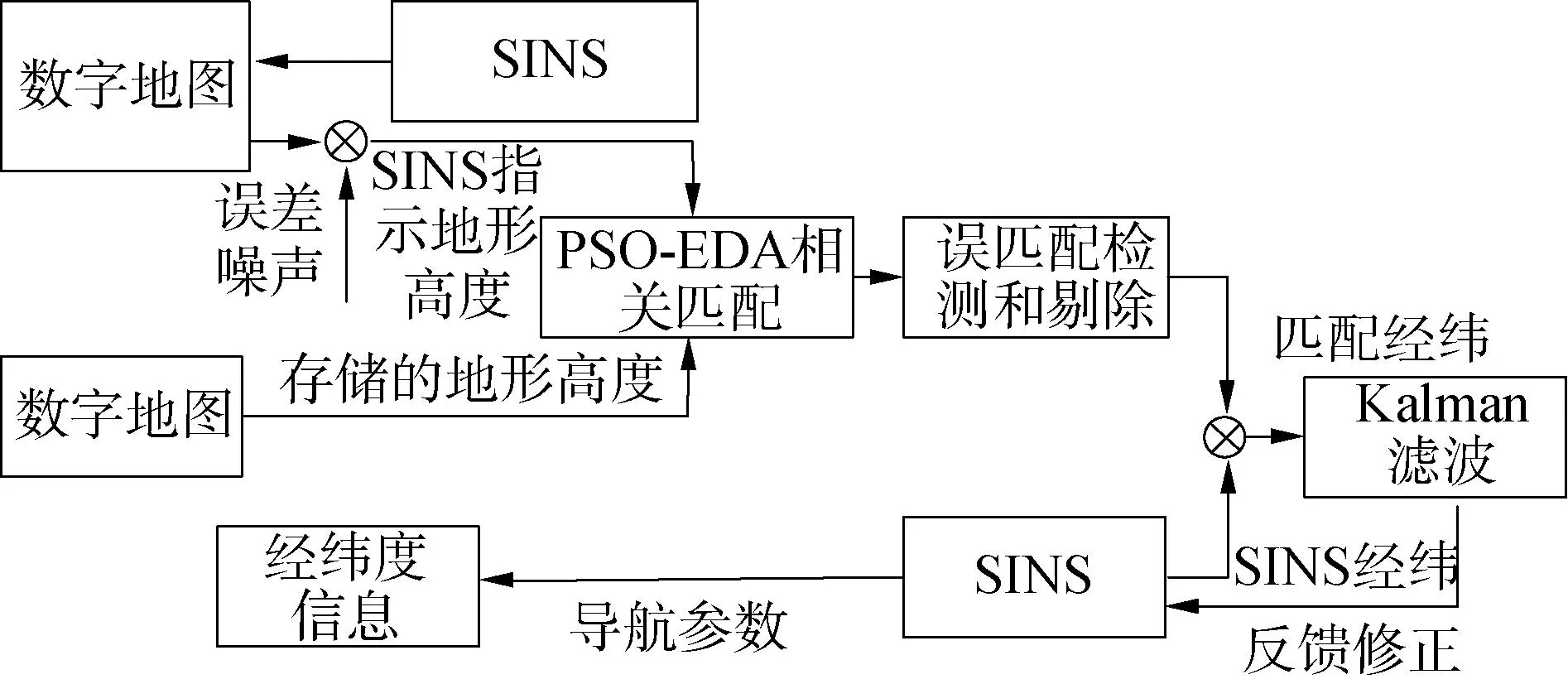
图6 TAN松组合系统结构Fig.6 Structure block diagram of TAN loose combination system

TERCOM误差受数字地图分辨率、高度表测量误差等综合影响,没有明确的数学模型,故选取捷联惯性导航系统的状态量为组合导航系统的状态变量。

选择捷联惯导系统的位置误差、速度误差、姿态误差、陀螺漂移和加速度计零偏作为状态量[17]:

(6)

根据捷联惯导系统的误差方程,可得地形辅助导航系统的状态方程为[18]:

(7)

式中:A为状态矩阵;G为状态噪声矩阵;W为噪声矢量。

选择地形匹配位置与捷联惯导系统解算的位置作为地形辅助组合导航系统的量测量:

(8)

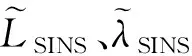
根据式(6)、(7)建立的状态模型与量测模型,便可使用Kalman滤波算法对SINS进行位置校正。

4 仿真及分析

4.1 基于优化PSO算法的TERCOM方法仿真验证

本文仿真中基于优化PSO算法的TERCOM方法与基于MSD算子的传统TERCOM方法的匹配成功率与单次匹配时间进行对比,除匹配算法外,其余仿真参数保持一致。实验区域选为四川甘孜州雅江县,地图范围为北纬30°～30.15°,东经100°～100.15°。

设UAV以30 m/s的速度匀速航行,高程的采样间隔为1 s,航行时间为400 s,整段航迹共有500个采样点,为保证第1次和最后一次匹配时有足够的实测序列,采样至第30个采样点位置后开始匹配,整段航迹分为44个等长的匹配序列。实测高程序列由真实高程值加误差形成,搜索区域大小由3.2节的搜索区域确定方法给出。改进PSO算法参数设置如表1所示。

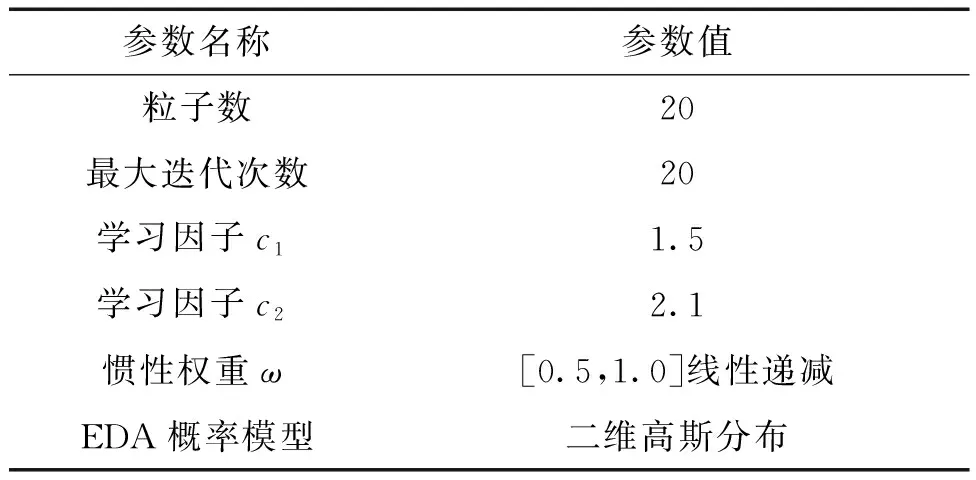
表1 优化PSO算法主要参数Table 1 The main parameters of optimize PSO algorithm

基于优化PSO算法的TERCOM方法与基于遍历算法的传统TERCOM方法的匹配结果如图7所示,匹配误差如图8所示。设进入匹配区时SINS位置误差为300 m,每次匹配的搜索范围为1 200 m×1 200 m的正方形区域,共1 600个基准子图。

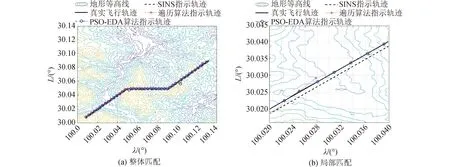
图7 优化PSO算法/遍历算法匹配结果Fig.7 Optimize PSO algorithm/traversal algorithm matching results

图8 优化PSO算法/遍历算法匹配误差Fig.8 Optimize PSO algorithm/traversal algorithm matching error

基于优化PSO算法的TERCOM方法与传统TERCOM方法的匹配成功率与单次匹配时间对比如表2所示。

表2 2种匹配算法的地形匹配结果比较Table 2 Comparison of terrain matching results of two matching algorithms

由表2可直观看出:基于遍历的传统TERCOM算法的平均每次匹配时长为0.001 1 s,基于优化PSO算法的TERCOM方法平均每次匹配时长为0.000 3 s,仅约为传统TERCOM算法的1/3,并且匹配成功率更高。因此基于优化PSO算法的TERCOM是有效的,在实际应用中更具优势。

4.2 基于航迹规划的无人机地形辅助导航仿真

通过比较未进行航迹规划的地形辅助导航与引入航迹规划的地形辅助导航的导航结果,验证在无人机任务区间包含非匹配区时,基于航迹规划的地形辅助导航具有更高的导航精度。地形匹配算法为本文提出的基于改进PSO算法的TERCOM方法。仿真主要参数如表3所示。

表3 TAN主要参数Table 3 Main parameters of TAN

设UAV的航行起点为东经107.1°,北纬33.2°,终点为东经107.7°,北纬33.7°,进行2次仿真实验,实验1为未进行航迹规划的地形辅助导航,为对照组,实验2为航迹规划后的地形辅助导航。为保证采集到足够的实测高程序列,从100 s开始进行地形轮廓匹配。如图9所示,2条轨迹的起点与终点相同,航行区间内有大量的地形平坦区域,即图中地形等高线稀疏的区域。

图9 航迹规划前后地形辅助导航轨迹对比Fig.9 Comparison of terrain-aided navigation trajectories before and after track planning

航迹规划前后地形辅助导航轨迹对比如图9所示,如果UAV从任务起点直线飞行至目标点,则途中经过大量地形平坦区域,未进行航迹规划时的地形辅助导航位置误差如图10所示。经过航迹规划后,UAV绕过地形平坦区域航行至目标点,位置误差如图11所示。

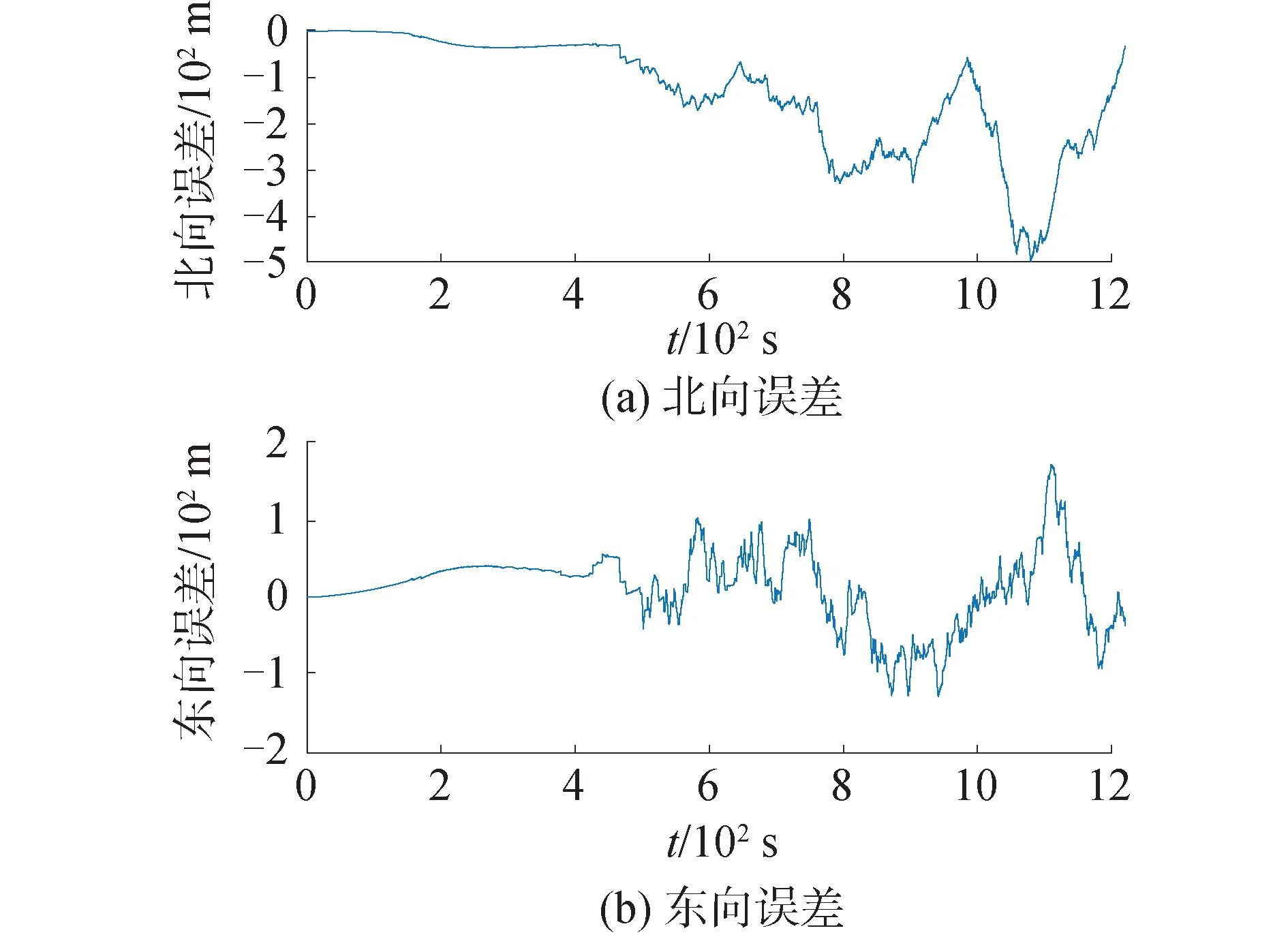
图10 未航迹规划的地形辅助导航位置误差Fig.10 Terrain aided navigation position error without track planning

图11 航迹规划后的地形辅助导航位置误差Fig.11 Terrain-aided navigation position error after track planning

图10中,未加航迹规划的地形辅助导航的最大位置误差为496 m,而在飞行前进行航迹规划,使UAV的航线避开地形平坦区域后,最大定位误差仅为71 m,航迹规划路径上的定位误差仅为未规划航迹路径上的1/7。

5 结论

1)本文针对传统地形辅助导航受地形影响大和实时性差的问题,提出基于航迹规划的无人机地形辅助导航方法。

2)在飞行前首先结合地形特征进行航迹规划,在搜索匹配时充分利用粒子群优化算法的快速寻优能力,并采用分布估计算法辅助更新粒子群算法中种群的分布,达到快速匹配和定位,提高了导航系统的综合能力。

3)仿真分析表明,基于优化PSO算法的地形匹配算法的单次匹配用时明显低于传统TERCOM算法,且经过预先航迹规划的地形辅助导航算法的匹配精度明显优于未经过航迹规划的地形辅助导航算法。