机构动作可靠性估计的自适应极值响应面法

文浩, 侯保林

(南京理工大学 机械工程学院, 江苏 南京 210094)

机构动作可靠性是指机构在规定的使用时间和规定的使用条件下,精确、及时、协调地完成规定动作的能力[1]。机构在制造、装配和使用阶段普遍存在不确定性,如加工误差、装配误差、载荷变化、零部件磨损以及外部扰动等,会导致机构动作输出性能存在不确定性。如何对不确定性下的机构动作可靠性进行估计是机构动作可靠性分析的重要内容。近年来在兵器和航空航天等领域,专家学者们基于概率可靠性理论,考虑参数的随机不确定性,对弹药协调器[2]、导弹折叠翼[3]、飞机起落架[4]等机构的动作可靠性进行了估计。但是在机构研制阶段与前期使用阶段,一些不确定性参数由于数据信息不足,无法获得其概率分布,只能给定取值范围,甚至一些不确定性参数在机构一次动作过程中就是变化的,直接将其处理为服从概率分布的随机变量会引起可靠性分析的不客观与不准确。

目前针对随机-区间混合不确定性可靠性的研究主要集中在结构可靠性领域,所采用的方法大体可以分为2类:1)通过增加或减少不确定性变量的信息,将混合不确定性变量转换到统一量化模型的基础上解析求解可靠度[5-6];2)采用两步法求解可靠度区间[7-8],第1步求解区间变量空间下功能函数的极大值和极小值,第2步计算随机变量空间下可靠度的上下界。对于复杂机构而言,功能函数一般难以显式表达,大多通过仿真模型计算得到[2-4],因此可以采用第2类方法求解随机-区间混合不确定性下的机构动作可靠度区间。

响应面模型是解决可靠性分析计算量高的主要方法之一,其精度和效率取决于响应函数的类型和试验点的选取。响应面建模主要有多项式法、Kriging函数法、支持向量机和神经网络等,目前尚无明确的结论表明哪种方法在所有问题中都优于其他方法,因此在不明确实际问题的非线性特性时尽量选择适用范围较广的方法进行建模。近年来众多神经网络算法被用于构建响应面模型[9-11],表现出了较好的适用性与准确性。在可靠性分析中重点要求响应面模型在靠近极限状态曲面的局部具有很高的拟合精度,因此使用传统的单阶段抽样方法的效率很低。为此许多学者使用基于主动学习理论的加点准则进行序列采样,其思路是选取靠近极限状态曲面的试验点对响应面模型进行更新迭代,能够在保证精度的前提下提高计算效率。目前针对Kriging模型已经提出了一系列高效加点准则[12-14],但均因涉及协方差计算,无法应用于其他类型的响应面模型。对此李国发等[15]提出了一种基于通用学习函数的加点策略,能够适用于多种响应面模型。

综上所述,本文利用极值响应面(extremum response surface, ERS)思想将随机-区间混合不确定性下的机构动作可靠性估计问题转换为随机变量下的可靠度区间边界问题,设计了一种自适应极值响应面(adaptive extremum response surface, AERS)方法进行高效求解。将麻雀搜索算法(sparrow search algorithm, SSA)和混合核极限学习机(mixed kernel extreme learning machine, MKELM)与ERS相结合,并利用基于主动学习与反向学习的自适应加点策略(adaptive infilling strategy, AIS)对ERS进行更新,进而通过蒙特卡罗仿真(Monte Carlo simulation, MCS)获取机构动作可靠度的上下界。

1 AERS-MCS方法

1.1 混合不确定性下的机构动作可靠性问题

以实现动作为目的的机构通常具有输出参数要求。设机构动作的输出参数为φ,相应的许用值范围为[φ-,φ+],影响机构动作的不确定性参数为ξ=[ξ1ξ2…ξr],则一般地φ为ξ的隐式函数,输出参数达到规定要求的概率为:

R=P(φ-≤φ(ξ)≤φ+)

(1)

大多情况下,机构动作的输出参数误差范围定义为±ε0,ε0为允许的最大误差。当系统不确定性参数包含随机变量和区间变量时,满足下列条件表示系统动作可靠:

z=g(X,Y)=ε0-|ε(X,Y)|≥0

(2)

式中:X=[X1X2…Xn]为n个已知概率分布的随机变量组成的向量;Y=[Y1Y2…Ym]为m个区间变量组成的向量;z=g(X,Y)为极限状态函数(limit state function, LSF);ε(X,Y)为不确定性变量下动作输出参数的误差。

由于区间变量的存在,极限状态曲面由不确定性参数空间中的一个曲面拓展为由下边界和上边界构成的一个区域[7],相应的动作可靠度将变为一个区间数,其下界和上界可以表示为:

0|X∈ΦR,Y∈ΦI)

(3)

0|X∈ΦR,Y∈ΦI)

(4)

式中:Rmin和Rmax分别为动作可靠度的上界和下界;zmin(X)和zmax(X)分别为区间变量Y下的LSF极小值和极大值;ΦR为随机变量X的变量空间;ΦI为区间变量Y的变量空间。通常动作可靠性更关注可靠度区间的下界,因此本文对Rmin的分析过程进行阐述。

1.2 基于ERS-MCS的可靠度区间求解

ERS方法目前主要应用于柔性机构的结构可靠性分析[16-17],本文利用ERS的思想处理同时存在随机变量X和区间变量Y的机构动作可靠性分析问题,通过建立从随机变量X到LSF响应极小值或极大值的ERS获取可靠度的下界或上界。利用ERS求解动作可靠度下界Rmin的具体过程如下:

1)选取初始样本。拉丁超立方抽样能够兼顾多维空间和单维尺度下样本的分布均匀性,在选取初始样本时使用该方法分别在随机变量X和区间变量Y的变量空间内选取S个初始样本,随机变量Xi(i=1,2,…,n)的样本为x1i,x2i,…,xSi,区间变量Yj(j=1,2,…,m)的样本为y1j,y2j,…,ySj。

2)构建初始响应面(initial response surface, IRS)。将初始样本[xs,ys],s=1,2,…,S输入仿真模型计算得到相应的动作输出参数,并计算LSF响应值g(xs,ys)。基于初始样本[xs,ys]和响应值g(xs,ys)的数据集ψIRS,构建IRS:z*=g*(X,Y)。

3)求取LSF响应极值。对于初始样本[xs,ys],保持样本中的随机变量xs=[xs1xs2…xsn]不变,利用优化算法调用IRS求取在区间变量Y的变量空间ΦI内LSF的响应极值:

(5)

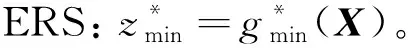
5)计算动作可靠度下界。基于构建好的ERS,进行MCS计算得到Rmin:

(6)

式中:NMCS为MCS抽样数目;I(·)为指示函数。

1.3 结合主动学习与反向学习的AIS

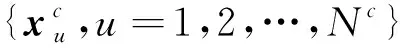
(7)

(8)

(9)

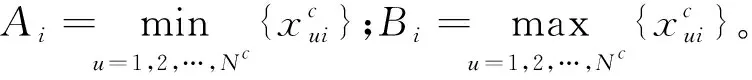
基于上述结合主动学习和反向学习的AIS更新ERS的具体步骤如下:

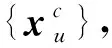
z*=g*,τ(X,Y)

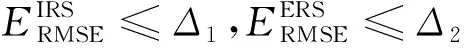
考虑随机-区间混合不确定性时,基于本文提出的AERS-MCS的机构动作可靠度下界的分析过程如图1所示。类似地可以计算机构动作可靠度的上界,进而得到机构动作可靠度区间。

图1 AERS-MCS计算流程Fig.1 Calculation process of AERS-MCS

2 基于SSA-MKELM响应面模型

2.1 MKELM

核极限学习机是基于极限学习机理论与核函数的单隐含层神经网络,具有影响参数少,学习速度快和泛化能力强的特点,能够用于构造复杂的非线性替代函数[18]。设极限学习机输入层、隐含层和输出层分别有L、H和O个节点,N个独立样本中第k个样本的输入为pk=[pk1pk2…pkL],输出为qk=[qk1qk2…qkO];第h个隐含层节点偏置为bh,与输入层节点的连接权值为ωh=[ωh1ωh2…ωhL],与输出层节点的连接权值为βh=[βh1βh2…βhO]。若隐含层节点的激活函数为gh(·),则有:

Hβ=Q

(10)

式中:β=[β1β2…βH]T为隐含层与输出层的连接权值矩阵;Q=[q1q2…qN]T为网络输出矩阵;H为隐含层输出矩阵,H=[gh(p1)gh(p2)…gh(pN)]T;gh(pk)=[gh(ω1·pk+b1)gh(ω2·pk+b2)…gh(ωH·pk+bH)]。

根据岭回归原理,为了提高网络的泛化性能,求解β需要同时考虑经验风险最小和结构风险最小,即引入正则化系数γ:

(11)

根据卡罗需-库恩-塔克条件求解可得:

(12)

训练样本pk对应的网络输出为:

(13)

为了避免隐含层随机性的影响,基于Mercer定理,定义核矩阵为:

Ω=HHT:Ωkλ=K(pk,pλ)=g(pk)g(pλ)

k,λ=1,2,…,N

(14)

则训练样本pk对应的网络输出为:

(15)

式中Ωk=[K(pk,p1)K(pk,p2)…K(pk,pN)]。

由式(15)可知引入核函数后,不再需要确定隐含层节点数目,避免了隐含层节点参数随机性的影响。核极限学习机的性能主要取决于正则化系数与核函数的类型及其参数。常用的核函数有:

KPoly(pk,pλ)=(pk·pλ+l)χ

(16)

(17)

式中:KPoly和KRBF分别为多项式核函数和高斯核函数;l、χ和σ为相应的核函数参数。

引入权重系数φ,φ∈[0,1],构建混合核函数为:

K(pk,pλ)=φKPoly+(1-φ)KRBF

(18)

基于该混合核函数的MKELM能够兼顾学习能力与泛化能力,有利于提高其预测精度。

2.2 SSA优化的MKELM

本文提出的AERS-MCS方法中,需要多次利用MKELM构建响应面模型,手动调节MKELM的参数是不可行的,因此采用SSA对其参数进行寻优选取以自动构建性能最优的响应面模型。此外计算过程中LSF响应极值也是使用SSA求解得到的。

SSA是一种新型群智能优化算法,通过模拟麻雀群体智慧、觅食和抗捕食行为来获取最优解,具有实现简单、易于扩充和自组织性等优点[19]。麻雀觅食的过程可以理想化为发现者-加入者模型,发现者搜索能力强,负责寻找食物并引导种群觅食,加入者跟随发现者进行觅食,同时部分加入者会监视发现者以获得更好的觅食区域。当种群意识到有捕食者时边缘的麻雀会向安全区域移动。

设D维搜索空间中,种群由W只麻雀组成,其中发现者比例为ap,加入者比例为aJ=1-ap,警戒者比例为aA。第w(w=1,2,…,W)只麻雀位置为ow=[ow1ow2…owD],适应度值为f(ow)。

在每次迭代过程中,发现者的位置更新为:

(19)

加入者的位置更新为:

(20)

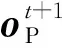
意识到危险的麻雀位置表示为:

(21)

使用SSA在MKELM的参数相应的取值空间ΦMKELM内对进行寻优选取。测试集样本预测值与真实值的均方根误差ERMSE越接近0,决定系数R2越接近1,则MKELM的拟合优度越好,将ERMSE与R2的比值θ定义为MKELM的评价指标,则SSA-MKELM的数学模型表示为:

(22)

其完整流程如图2所示。

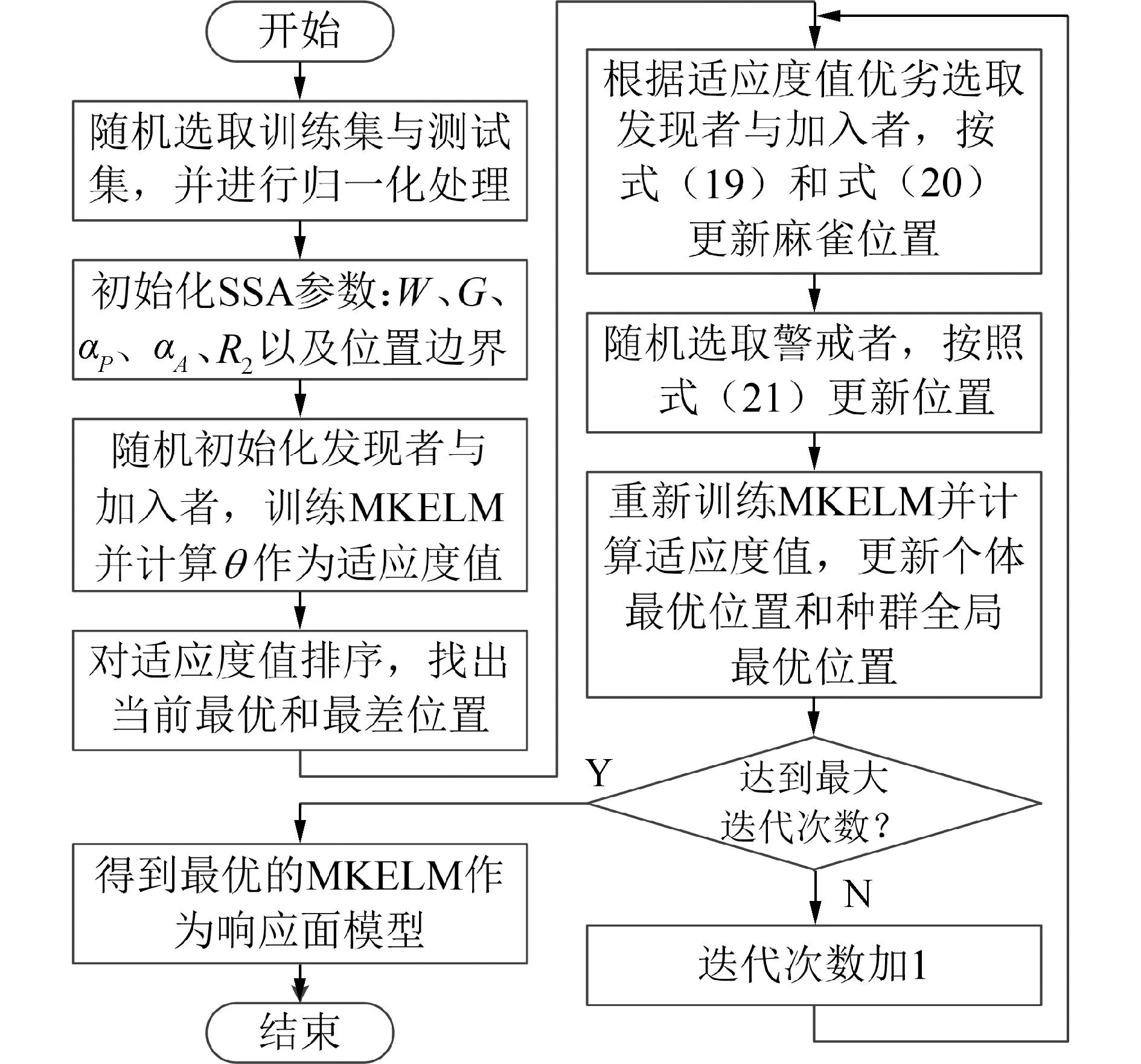
图2 SSA-MKELM算法流程Fig.2 SSA-MKELM algorithm flow

3 算例分析

3.1 数值案例

为了验证所提AERS-MCS方法的有效性,首先以一个三维非线性数值案例进行说明,设LSF为:

g(x1,x2,y1)=

(23)

式中:ε0=2;随机变量x1、x2和区间变量y1相互独立,x1～(1,0.2),x2～(2.5,0.1),y1∈[1.4,1.6]。

使用Monte Carlo抽样法产生105个随机变量x1和x2的样本点,然后对每个样本点抽取100个区间变量y1的样本点,进而计算得到LSF的极大值与极小值,由此求得的动作可靠性上下界分别为0.954 0和0.807 5,将其作为近似精确解。

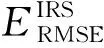
表1 数值案例中动作可靠度计算结果Table 1 Action reliability calculation results in numerical case

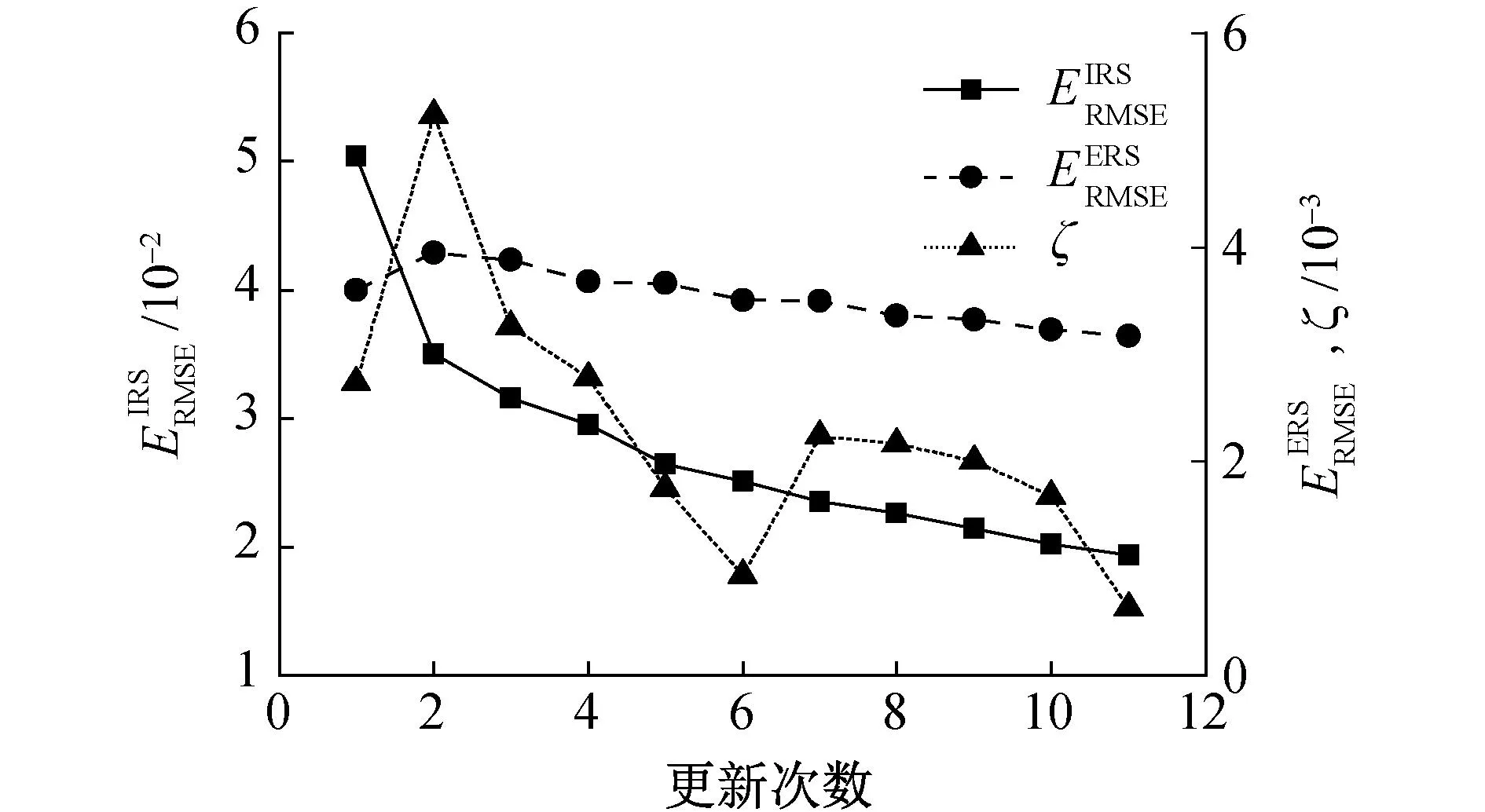
图3 数值案例ERS更新过程Fig.3 ERS update process in numerical case

图4 数值案例样本点分布Fig.4 Sample points distribution in numerical case

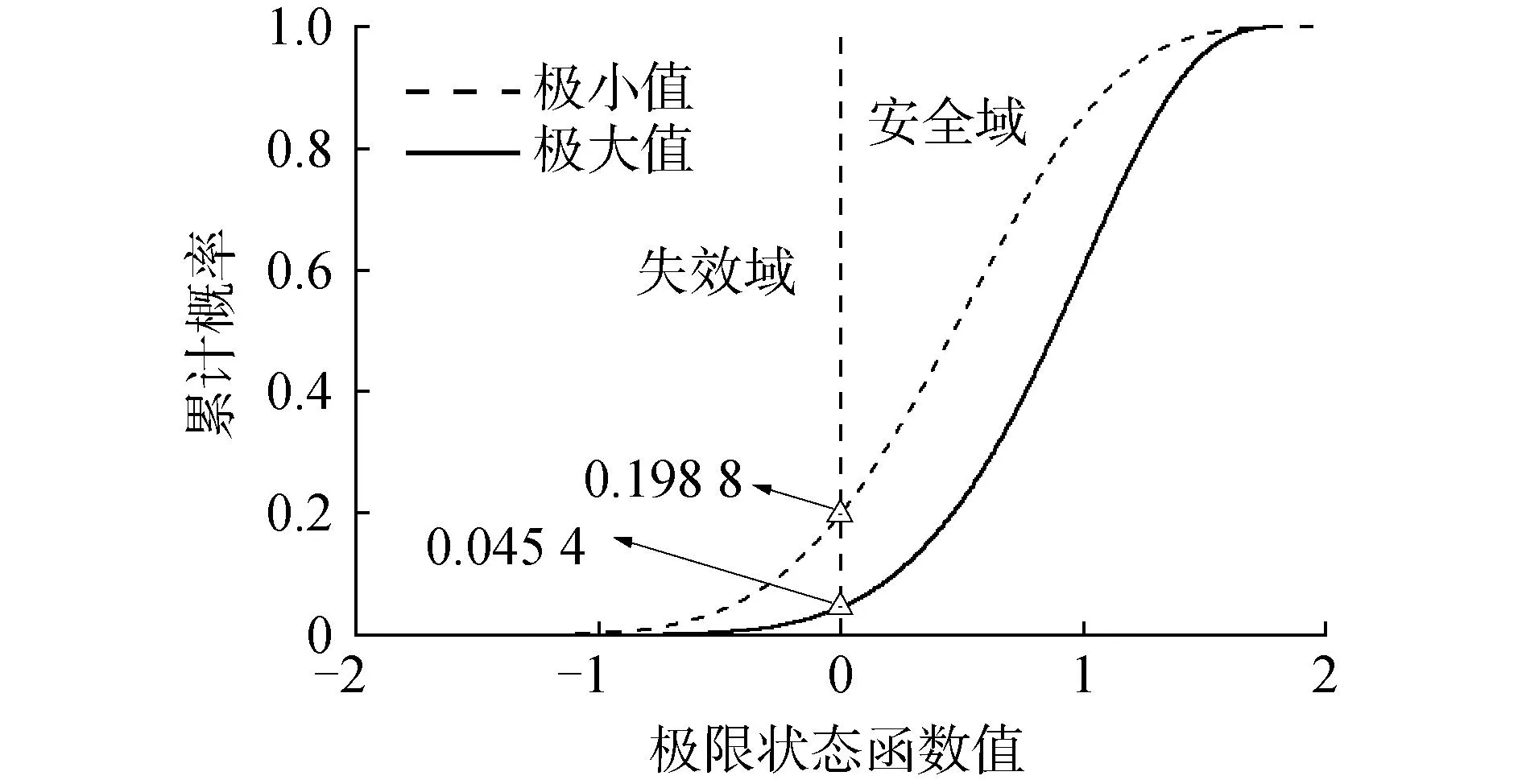
图5 数值案例LSF极值累计概率分布曲线Fig.5 Cumulative probability distribution curve of LSF extremum in numerical case

3.2 工程案例

某武器平台内部常采用链式回转输送装置进行负载的贮存与传输,在其设计阶段需要对动作可靠性进行估计。图6为某链式回转输送装置的原理样机结构,主要包括底板、主动链轮、从动链轮、链条、导轨、负载、驱动电机和减速器等。驱动电机经过减速器带动主动链轮转动,8个负载等间距固定在回转链条上,链条在主动链轮的带动下沿圆弧形导轨运动,主动链轮旋转180°为一个间距的负载输送过程;固定负载的链节下端安装有带滚轮的组合轴承,用以支撑回转部分的主要质量。

根据回转链式输送机的拓扑结构,在ADAMS软件中建立多刚体动力学模型,其中滚轮与轨道、链条滚子与链轮、导轨之间均为实体接触,接触力采用基于赫兹接触定律的非线性等效弹簧阻尼模型计算;考虑路面不平度引起的武器平台外部扰动,以图7中的速度曲线作为垂直方向(图6中x轴方向)扰动,角速度曲线作为俯仰方向(图6中绕y轴方向)扰动。采用比例微分控制算法,在Simulink中建立包含机械系统与控制系统的联合仿真模型,模型中的参数按照名义值或理论值设定,并以此为标准状态,进行满载情况下一个间距的负载输送过程仿真,得到的主动链轮角位移曲线如图8所示。

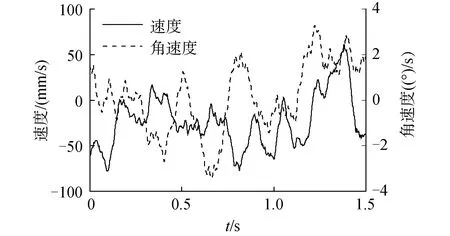
图7 扰动曲线Fig.7 Disturbance curves

图8 主动链轮角位移曲线Fig.8 Angular displacement curve of driving sprocket

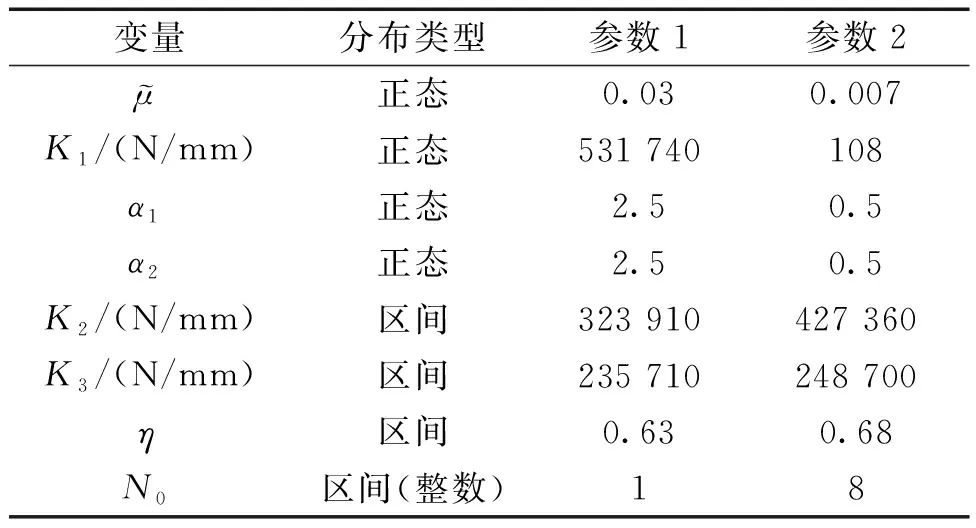
表2 不确定性变量的分布Table 2 Distribution of uncertainty variables

规定回转链式输送机在不超过1.5 s的时间内旋转180°,且允许的最大定位误差ε0=1°,否则判定其动作失效。根据式(2)可将回转链式输送机的动作可靠性的LSF表示为:

(24)

表3 不同方法构建的IRSTable 3 IRS constructed using different methods

图9 工程案例ERS更新过程Fig.9 ERS update process in engineering case

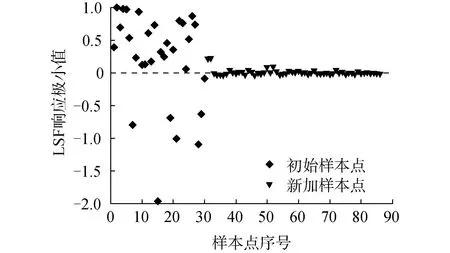
图10 工程案例样本点分布情况Fig.10 Distribution of sample points in engineering case

图11 工程案例LSF极值累计概率分布曲线Fig.11 Cumulative probability distribution curve of LSF extremum in engineering case

表4 动作可靠度计算结果Table 4 Action reliability calculation results

4 结论

1) 针对在研制阶段与前期使用阶段数据信息不足导致机构存在随机-区间混合不确定性的情况,提出了一种动作可靠度估计的AERS-MCS方法。利用ERS思想将随机-区间混合不确定性下动作可靠性估计问题转换为可靠度上下界求解问题,具有很高的计算效率。

2) 利用结合主动学习和反向学习的AIS对ERS进行更新,能够使ERS在极限状态曲面附近具有较高的拟合精度;使用SSA-MKELM构建的响应面模型具有较高的预测精度,有利于快速得到满足精度要求的响应面模型。

3) 所提方法为随机-区间混合不确定性下机构动作可靠性的估计提供了一种参考,随着区间不确定性变量信息量的不断增加,当可以获取其变化规律和概率分布时,动作可靠度区间将进化为动作可靠度值。