基于相位变化率的体目标与点源合成目标回波分辨

雍锦涛, 莫世奇, 陈云飞, 王振山, 贾兵, 李桂娟, 张阳

(1.哈尔滨工程大学 水声工程学院, 黑龙江 哈尔滨 150001; 2.水下测控技术重点实验室, 辽宁 大连 116013; 3.大连理工大学 信息与通信工程学院, 辽宁 大连 116024)

水下目标声学模拟诱骗主要包括回声特性模拟诱骗和噪声特性模拟诱骗,是水下平台应对声自导鱼雷攻击的重要对抗手段。回声特性模拟主要是通过数个代表体目标典型亮点的应答转发换能器按照一定的加权系数对接收到的入射波信号进行幅度和相位加权后转发,经叠加形成真实目标的模拟回波,实现对主动声自导鱼雷的诱骗和干扰[1-5]。多点源合成目标能够较好地模拟真实体目标的亮点分布、尺度等特性,对主动声自导鱼雷具有很强的诱骗干扰能力,使得水下真假目标分辨面临极大的挑战,如何对真实目标和点源合成目标回波进行有效辨识是水下目标探测识别的关键技术问题。

研究表明,声波经目标反射后产生回波,在回波产生的过程中,目标的几何形状、材质类别以及内部结构等物理属性参数对入射声波进行了波形调制[6],导致了声波波形的变化,即入射声波经目标散射后产生了与目标物理属性参数相关的相位跳变,也称为“目标相位”[7]。对于弹性目标而言,其本质是入射声波经目标散射后产生的几何散射波与弹性散射波相互叠加引起了入射声波的幅度和相位的调制变化。目标回波波形结构携带了目标的物理属性信息,回波相位特征则是表征目标回波波形结构的重要特征之一。多项用于目标探测、分类和识别的回波相位特征研究表明,回波相位特征可作为水中目标分类和识别的有效特征参量[8-17]。

多点源合成目标是一个非连续目标,可模拟真实体目标的典型亮点,无法模拟亮点之间的体目标散射特性变化,而真实体目标具有延伸表面和体积,其回波是由目标各连续部位反射的声波相干叠加生成,加之弹性表面波的存在,使得真实体目标和多点源合成目标模拟回波的波形结构存在较大的差异。

针对水中体目标回波与点源合成回波分辨问题,作者及其所在的研究团队前期开展了多项仿真和实验研究[18-20],研究表明目标回波波形结构、相移特性随着目标材质、结构、径向尺度的变化而具有显著区别,本文研究了体目标与多点源合成目标的回波相位特性,提出并建立了基于相位变化率的体目标与多点源合成目标回波的分辨方法,并通过Benchmark基准潜艇缩比模型和多点源合成目标模型的回声特性仿真和测试数据分析对其可行性进行了验证。

1 体目标与多点源合成回波相位特征差异性分析

体目标存在大量的散射点,其总体回波是由目标上不同部位散射分量叠加而产生。根据声呐目标亮点模型[21],可以将体目标分解成多个“亮点”,目标总体回波主要由这些“亮点”散射的子回波相干叠加生成。亮点主要分为几何亮点和弹性亮点,声信号经亮点散射,形成对应的几何散射波与弹性散射波,几何散射波与目标尺度、探测角度等因素相关,而弹性散射波与目标的材质和内部结构相关。对于单个亮点,其声散射过程的传递函数的表达式为:

H(r,f)=A(r,f)ej2πfτejφ

(1)

式中:A(r,f)为幅度反射因子;τ为时延因子;φ为亮点产生的“亮点相位跳变”。

设体目标由N个亮点构成,且将亮点产生回波这一过程看作线性系统,则当声信号S(f)经目标上N个亮点散射叠加形成的回波信号的表达式为:

(2)

当s(t)是线性调频信号时,其复数表达式为:

(3)

式中:τ为信号脉冲宽度;k=B/τ为线性调频斜率;B为信号带宽;rect(t/τ)是矩形调制函数。

对s(t)进行傅里叶变换,可得:

(4)

(5)

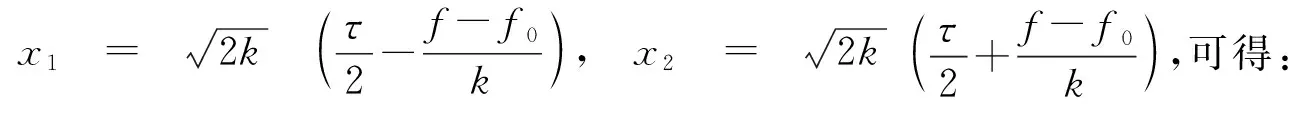
j[S(x1)+S(x2)])

(6)

式中C(x)和S(x)为菲涅尔积分。

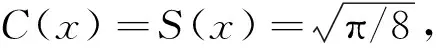
(7)

(8)

为便于分析,设A(ri,f)=A(f),则有:

(9)

对于M个点源合成目标而言,在固定观测点处,由不同时延的“规则包络结构”子回波信号叠加构成总体回波,其回波信号频域形式表达式为:

(10)

式中:τ1i为时延因子;B为点源信号幅度因子。

式(9)、(10)表明2类目标总回波的相位谱与声信号的频率和调频斜率等声信号参数紧密相关;对于体目标,其与各散射点的相对位置、亮点幅度以及“亮点相位”等声目标物理属性参数紧密相关,而点源合成目标不产生“亮点相位跳变”。特别地,当声波入射角发生变化时,体目标各散射点的散射回波在固定观测点处相干叠加形成的总体回波发生变化,回波的相位谱也发生变化,而单点源的散射回波不发生变化,且由于其无法模拟亮点之间的体目标散射特性变化,因此,与体目标回波相位的变化相比,多点源合成目标回波相位的变化相对不显著。

2 体目标与多点源合成回波的分辨方法

水下体目标回波的相位谱,与目标的几何结构尺寸、亮点幅度以及“亮点相位”等声目标物理属性参数紧密相关,而点源合成目标不产生“亮点相位”,且由于其无法模拟亮点之间的体目标散射特性变化,使得体目标回波相位谱与多点源合成目标回波相位谱存在明显的可分辨差异性。

为了凸显2类目标回波相位谱的差异性,并通过该差异性对2类目标的回波进行分辨,本文通过去除相位谱大的趋势量,增强相位谱变化小量,建立一种能够更好地凸显相位谱的高频起伏特性的表征参量,即相位变化率R:

(11)

式中:φ0为原始缠绕相位;φ为解缠绕后的相位;“UW”为相位解缠绕运算算子;f1和f2表示信号作傅里叶变换后的离散频域上相邻的2个频率;fs为信号采样频率;N为作傅里叶变换的点数。

基于上述差异性特征参量,设计体目标与点源合成目标回波分辨方法流程,如图1所示。

图1 体目标回波与多点源合成回波分辨方法流程Fig.1 Procedure of discrimination of under target echo and synthetic echo

具体为对回波数据作傅里叶变换,并采用具有相位不变性的全相位法获取目标回波频域相位[22],以单频复指数序列x(n)为例,对其做全相位傅里叶变换,得到其全相位快速傅里叶变换(FFT)频谱为:

(12)

由式(12)可知,全相位FFT谱的相位值为θ0,即为中心样点的理论值,与频偏m-k无关。由此可以看出,与传统FFT谱分析方法相比,全相位FFT谱分析方法能够极大地减少因数据截断而带来的频谱泄露,且具有相位不变性,相位信息保留完好,不会发生相位模糊,通过全相位FFT谱分析方法能够精确地提取出信号的相位信息。

随后对频域相位作解缠绕处理。一般情况下,通过频谱分析方法直接获得的相位是“缠绕相位”,即相位值周期调制在[-π,π]区间内,是剧烈跳变的,大部分情况下呈锯齿状。“缠绕相位”的不连续性或周期跳变性不属于信号本身所携带的信息,相位缠绕或混叠是由于计算相位的反正切函数的多值性引起了相位函数的跳变。因此,在提取相位特征前,需要对“缠绕相位”进行解缠绕处理,即根据反正切的主值和相位函数的周期性确定出合理的相位值。本文采用一种易于理解的相位解缠绕算法,即选定某参考点后,对于后续离散相位序列,若相邻离散相位值增量大于+π,则在现有值的基础上减掉2π,若相邻2个离散相位值的增量小于-π,则在现有值的基础上加2π,其他情况下,相位值保持不变。

在获取绝对相位的基础上,进一步经统计分析输出相位变化率,最终通过对比相同方位角度下的相位变化率量值,对体目标与多点源合成目标的回波进行分辨。

3 基于数值仿真的目标回波与模拟回波分辨方法验证

为了从理论上认识并掌握目标回波相位特征、验证方法的可行性以及特征参量的适用性,对回波相位变化率特征进行了仿真研究。

3.1 仿真参数及条件设置

采用Unigraphics优集三维几何建模软件对体目标进行几何建模,体目标几何模型采用Benchmark基准潜艇缩比模型[23],如图2所示。多点源合成目标模型示意如图3所示。

图2 1/20 Benchmark基准潜艇缩比模型Fig.2 1/20 Benchmark model of real target

图3 多点源合成目标模型Fig.3 Model of the synthetic point-source target

采用基于物理声学的板块元法[24]与频域间接法[25]对水下体目标的回波信号进行预报,得到目标回波时域波形。

多点源合成目标的回波模拟仿真,通过计算不同入射角度下的各点源应答子回波的到达设定的观测点的时间延迟、折算不同传播距离对应的声信号传播损失后,在固定观测点处叠加生成模拟目标的总体回波。

仿真参数设置:测试信号脉宽1 ms、频率为40～80 kHz的线性调频信号,方位角度0° ～180°。需要说明的是,本文中规定目标艏向为0°、正横位置为90°、目标艉向为180°。

3.2 仿真结果的分析与讨论

图4～6分别是0°、45°、90°入射角度下的Benchmark基准潜艇缩比模型体目标回波、相频谱。可以明显看出,不同角度下的时域回波波形结构显著不同,0°、45°入射角下的总体回波信号由存在明显的无回波信号间隔的2段信号组成,而90°入射角下的时域回波信号相对连续;其回波信号的相频谱存在明显的差异,0°入射角下的相频谱变化范围最大、90°入射角下的回波相频谱变化范围最小。图7～9分别是0°、45°、90°入射角度下的6点源合成目标回波、相频谱。可以明显看出,不同角度下的时域回波波形结构显著不同;其回波信号的相频谱存在明显的差异。

图4 Benchmark潜艇模型的回波与回波相位谱(0°入射角)Fig.4 Echo and phase spectrum of Benchmark model,(0° incidence angle)

图5 Benchmark潜艇模型的回波与回波相位谱(45°入射角)Fig.5 Echo and phase spectrum of Benchmark model(45° incidence angle)

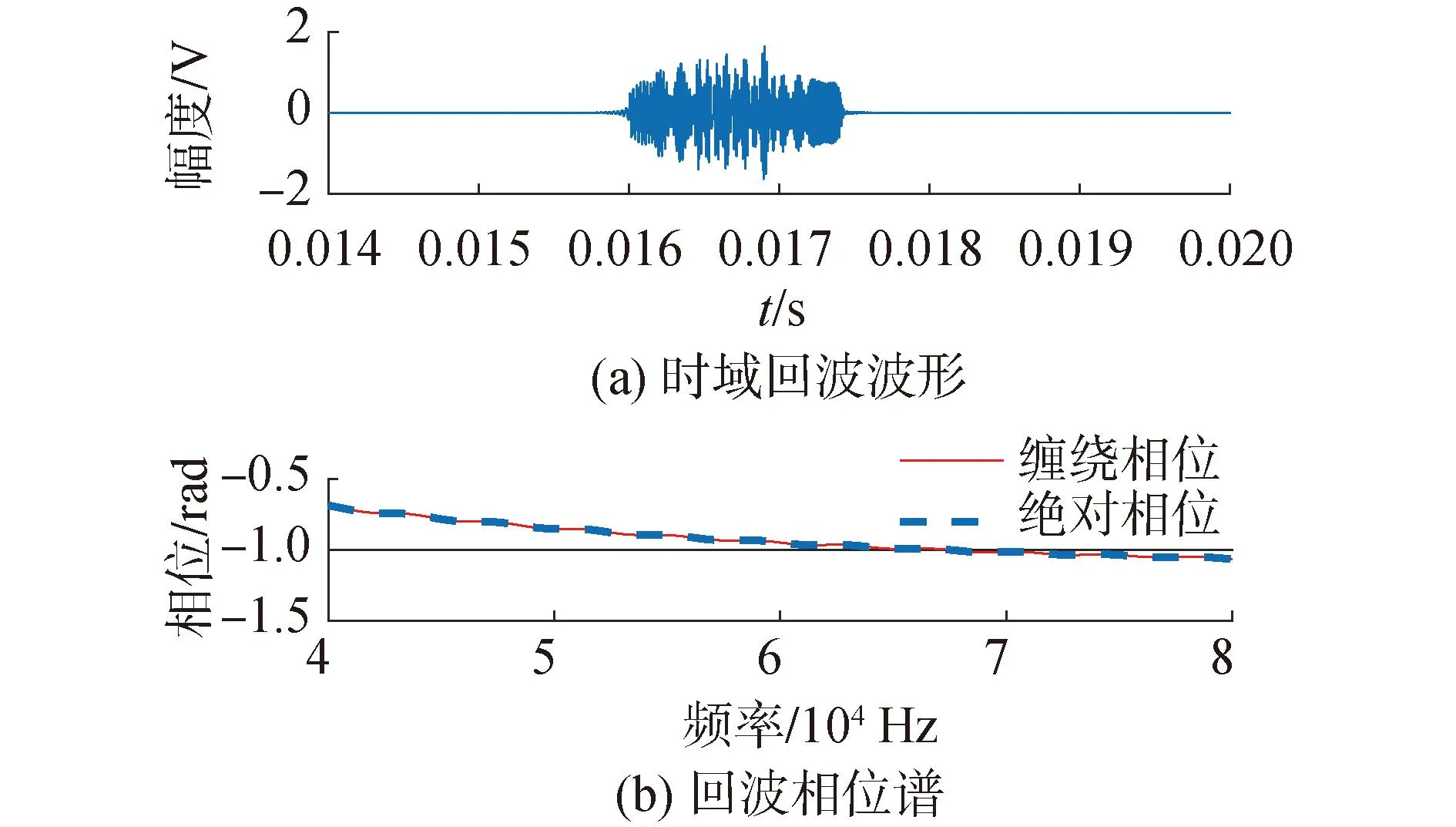
图6 Benchmark潜艇模型的回波与回波相位谱(90°入射角)Fig.6 Echo and phase spectrum of Benchmark model(90° incidence angle)

图7 6点源合成回波与回波相位谱(0°入射角)Fig.7 Echo and phase spectrum of the 6 point-source target(0° incidence angle)

图8 6点源合成回波与回波相位谱(45°入射角)Fig.8 Echo and phase spectrum of the 6 point-source target(45° incidence angle)

图9 6点源合成回波与回波相位谱(90°入射角)Fig.9 Echo and phase spectrum of the 6 point-source target(90° incidence angle)

进一步对2类目标回波的相频谱进行细化处理,得到相位随频率变化的变化率,如图10、11所示。由图10、11可知,2类目标均在90°入射角下的相位变化率最小,而0°、45°入射角下的相位变化率相对大;同一入射角度下,2类目标相位变化率随频率的变化起伏程度和频率均存在显著差异。

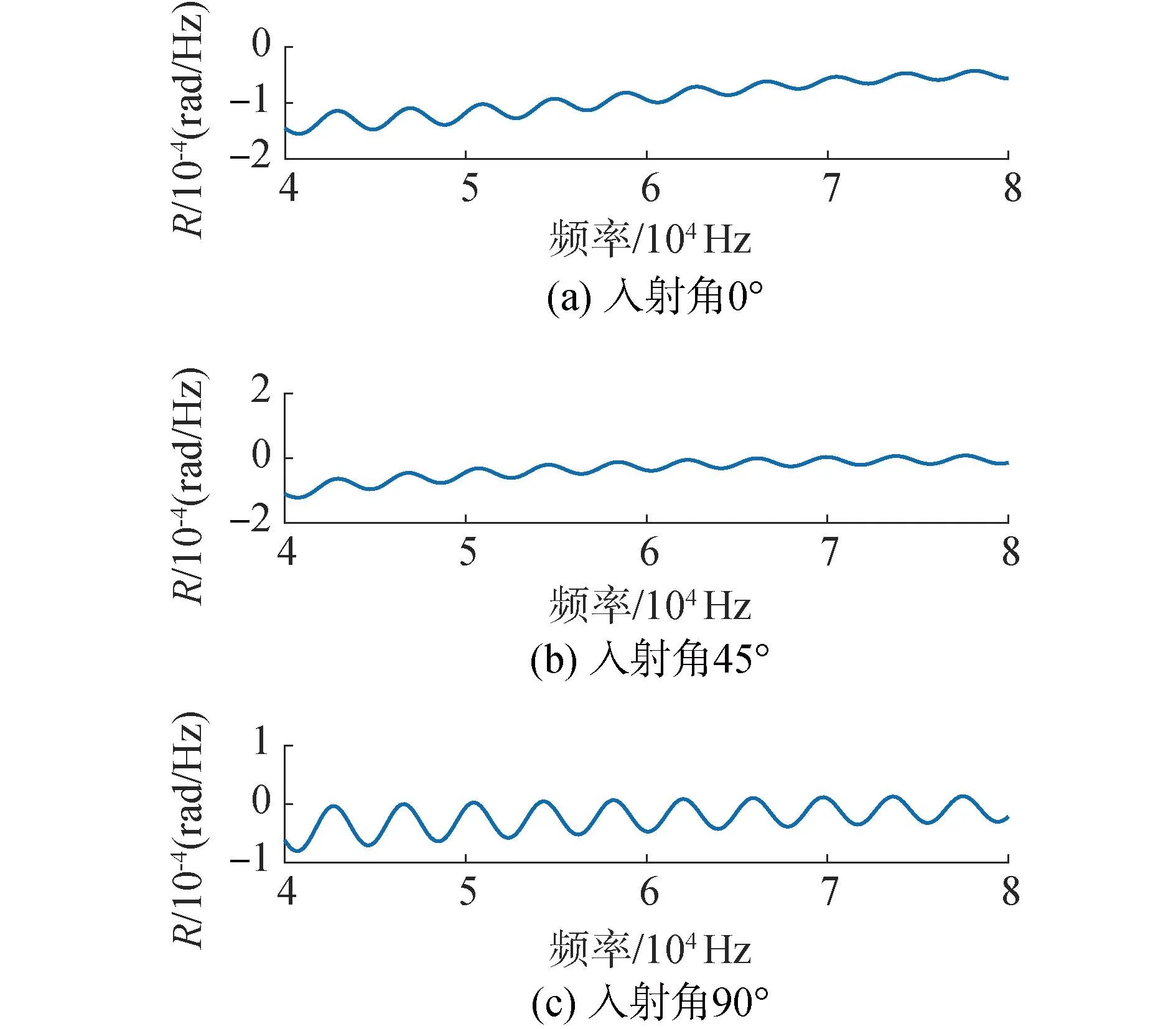
图10 Benchmark模型的回波相位变化率Fig.10 Change rate of phase of Benchmark model

图11 6点源合成目标的回波相位变化率Fig.11 Change rate of phase of the 6 point-source target

在图10、11的基础上,进一步统计分析处理,分别提取了体目标与多点源合成目标的0°～180°入射角内的回波相位变化率,如图12所示。

图12 Benchmark模型与多点源合成回波相位变化率对比Fig.12 Comparison of phase change rate between the Benchmark model and the point-source target

由图12可知,当声波从目标正横方位入射时,回波信号的绝对频域相位变化率相对小;当声波从目标艏艉方向入射时,其回波信号的绝对相位变化率相对大。当入射角由0°逐渐变化到90°,相位变化率总体上是逐渐减小的,当入射角由90°逐渐变化到110°,相位变化率总体上是逐渐增大的。在110°～180°内,体目标回波相位变化率在0.01～0.012内起伏变化,艏艉方向的相位变化率变化趋势和量值存在差异明显;而多点源模拟目标回波相位变化率的这一特点与构成合成目标的点源个数相关。特别地,如图12所示,入射角0°～180°内,同一入角度下,体目标回波相位变化率大于的多点源合成目标回波的相位变化率。

4 基于实验测试的目标回波与模拟回波分辨方法验证

4.1 实验测试参数设置

用于验证测试的体目标是缩放比为1/20的Benchmark体目标模型,模型长3.1 m;双点源合成目标是由2个独立声学特性参数几乎一致的应答器构成的。如图13、14所示,目标通过两根软绳吊挂在模型转台上,通过旋转平台改变模型相对于观测点的方位角,收发合置换能器布放在距目标等效声中心约11 m位置处,目标与换能器布放深度均为8 m。测试时,发射波束中心对准被测目标几何中心位置固定不动,目标从0°艏位置匀速旋转180°艉位置,同步采集目标回波测试数据。测试信号是脉宽为1 ms、频率为40～80 kHz的线性调频信号。

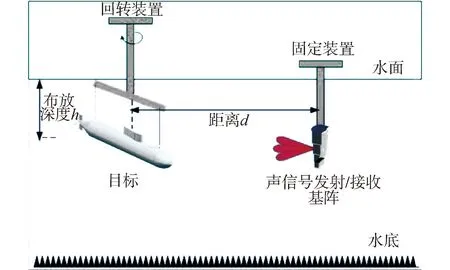
图13 Benchmark模型测试示意Fig.13 Configuration of test for Benchmark model

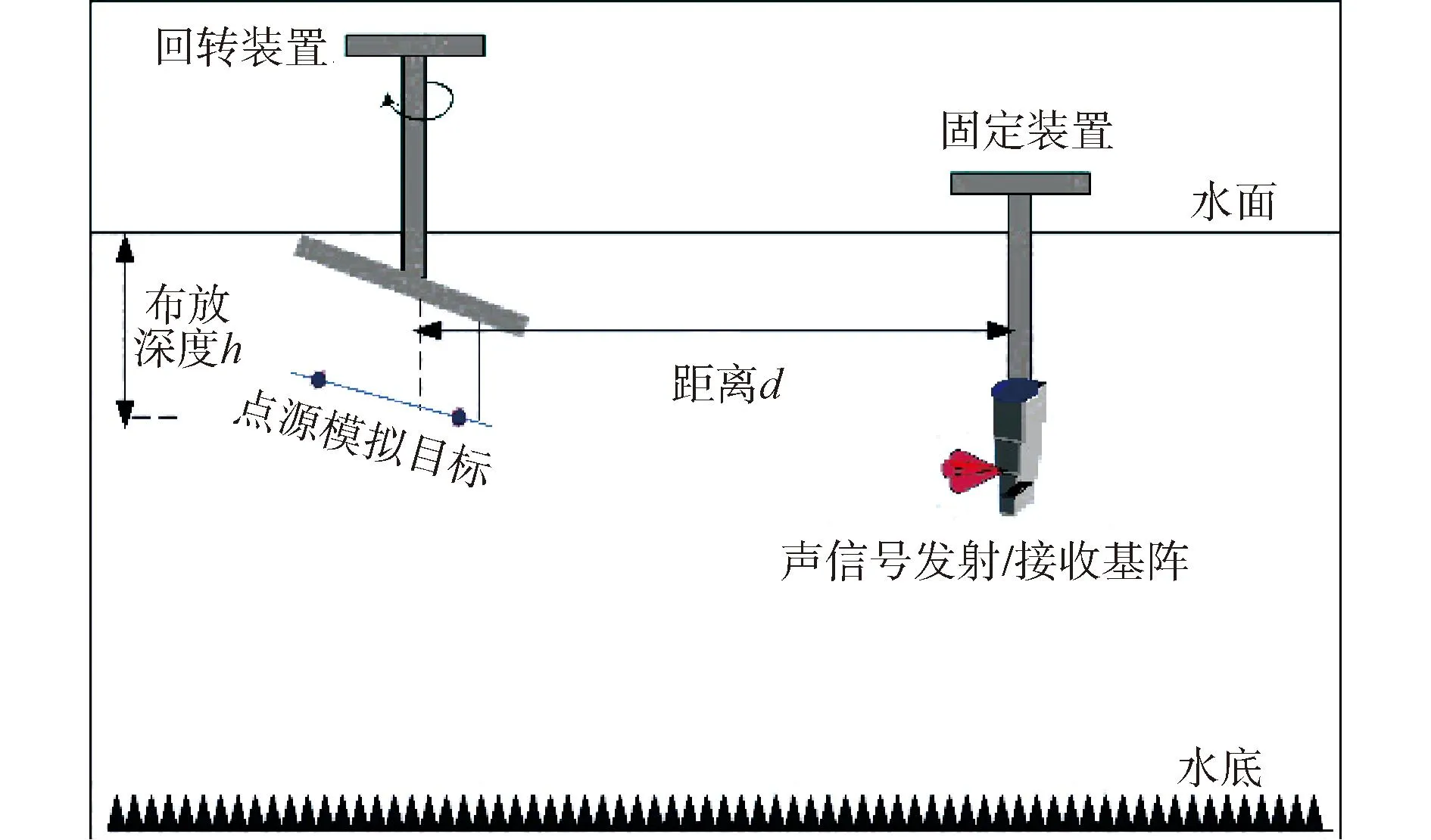
图14 双点源模拟回波测试示意Fig.14 Configuration of test for the point-source target

4.2 实验测试结果

图15～17是0°、45°、90°入射角度下的Benchmark基准潜艇缩比模型体目标的回波时域波形、回波相位谱。从图中可以看出,不同角度下的时域回波波形结构存在显著差异,0°、45°入射角下的总体回波信号存在明显的不连续性,而90°入射角下的时域回波信号相对连续且信号幅值相对较大。3个典型入射角度下,0°入射角下的相频谱变化范围最大、90°入射角下的回波相频谱变化范围最小,与理论仿真结果相符。

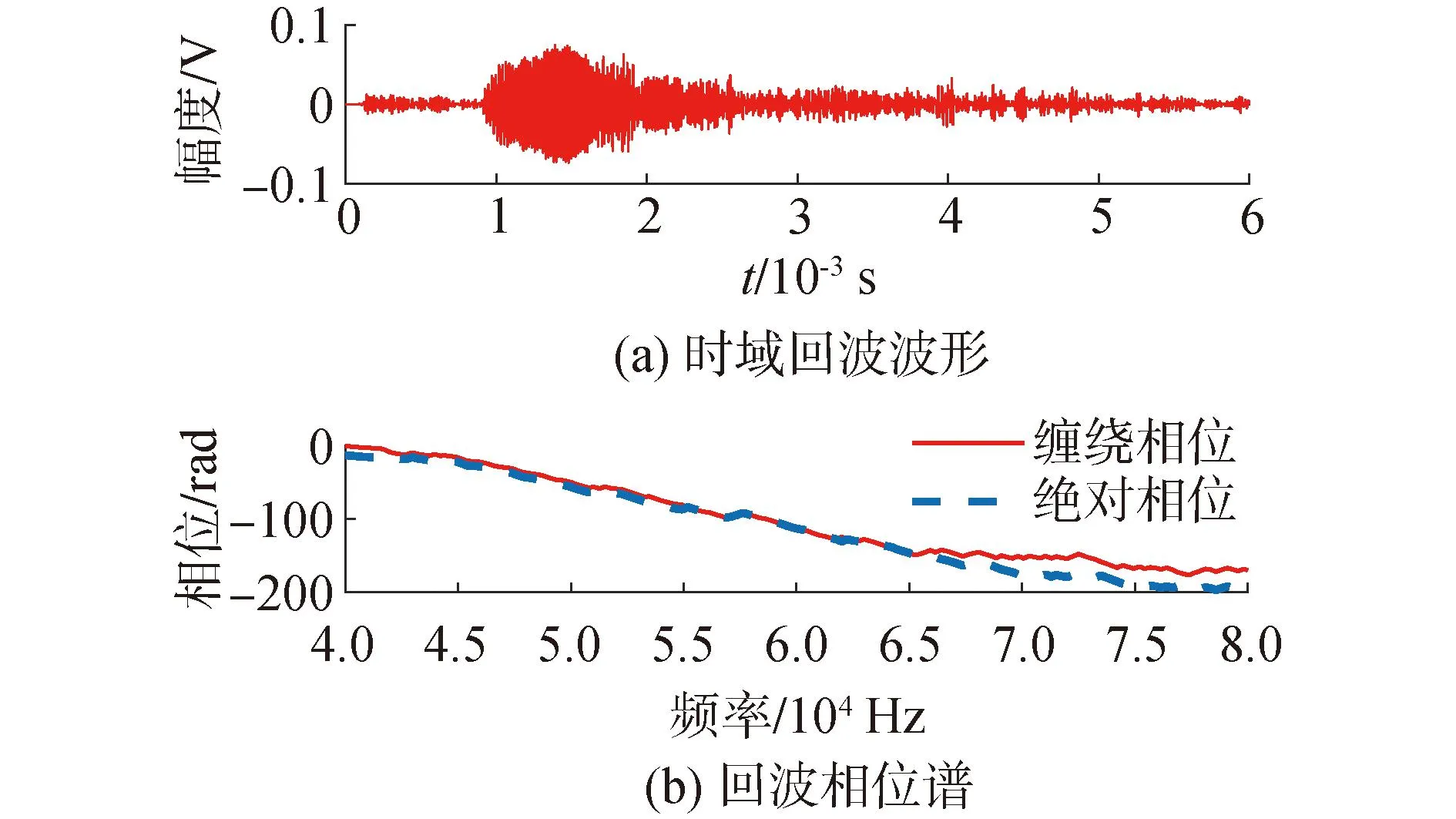
图15 Benchmark潜艇模型的回波与回波相位谱(0°入射角)Fig.15 Echo and phase spectrum of Benchmark model(0° incidence angle)

图16 Benchmark潜艇模型回波与回波相位谱(45°入射角)Fig.16 Echo and phase spectrum of Benchmark model(45°incidence angle)

图17 Benchmark潜艇模型回波与回波相位谱(90°入射角)Fig.17 Echo and phase spectrum of Benchmark model(90° incidence angle)

图18～20是0°、45°、90°入射角度下的双点源合成目标的时域回波、相频谱。可以明显看出,0°、45°入射角下的总体回波信号存在明显的不连续性,而90°入射角下的时域回波信号相对连续且信号幅值相对较大。0°、45°入射角下的相频谱变化范围相对小,90°入射角下的回波相频谱变化范围相对大,区别于体目标的实验测试与理论仿真结果。

图18 双点源合成回波与回波相位谱(0°入射角)Fig.18 Echo and phase spectrum of the 2 point-source target(0° incidence angle)

图19 双点源合成回波与回波相位谱(45°入射角)Fig.19 Echo and phase spectrum of the 2 point-source target(45° incidence angle)

图20 双点源合成回波与回波相位谱(90°入射角)Fig.20 Echo and phase spectrum of the 2 point-source target(90° incidence angle)

图21是0°、45°、90°入射角下的Benchmark体目标回波信号相位变化率。由图21可以看出,90°入射角下的相位变化率量值相对小、起伏程度低,而0°、45°入射角下的相位变化率量值相对较大、且起伏的频率和程度相对较大,与仿真计算结果的总体趋势相符。

图21 Benchmark模型的回波相位变化率Fig.21 Change rate of phase of Benchmark model

图22是0°、45°、90°入射角下双点源合成目标回波相位变化率。由图22可以看出,90°入射角下的相位变化率量值相对小、起伏程度低,而0°、45°入射角下的相位变化率量值相对较大、且起伏的频率和剧烈程度相对较大,此特点与Benchmark体目标模型的实验测试数据分析结果和仿真计算结果的特点类似,但是同角度下的量值存在明显差异。

图22 双点源合成目标的回波相位变化率Fig.22 Change rate of phase of the 2 point-source target

基于图21、22的结果,对每一入射角下的水下体目标与双点源合成目标的变化率进一步细化处理,分别得到两类目标在0°～180°入射角下的回波相位变化率,如图23所示。

图23 体目标与双点源合成目标回波相位变化率对比Fig.23 Comparison of phase change rate between the Benchmark model and the 2 point-source target

测试数据分析表明:与体目标相比,双点源合成目标在0°～180°入射角度范围内的回波信号的相位变化率相对小,两者间存在明显的量值差异和整体变化趋势的差异;同一入射角下,体目标回波相位变化率大于双点源合成回波的相位变化率,此结果与仿真结果相符合。

当声波从目标正横方位入射时,回波信号相位变化率小;声波从目标艏艉方向入射时,其回波信号相位变化率相对较大,与仿真分析结果一致。当声波入射方向在目标艏艉方向范围内时,测试数据分析结果与仿真分析结果的一致性较差;而在正横方位范围内,测试数据分析结果与仿真分析结果的一致性较好。造成差异的主要原因为:1)体目标回波仿真预报是通过板块元近似体目标表面得出的,且没有考虑目标内部结构的影响,使得部分回波信号相位信息缺失;2)在回波的仿真预报中,没有考虑混响等的干扰以及能量泄露的存在,使得测试数据分析结果和仿真分析结果存在一定的差异性。

4.3 体目标与多点源合成目标回波分辨

探测系统接收到水下体目标和点源模拟目标回波信号后,计算其回波的相位变化率和方位,根据掌握的先验知识,设置适宜的判决门限,利用目标回波的相位变化率与方位角度下的判决门限Th的大小关系来辨识目标为水下体目标回波还是点源模拟目标回波,如图24所示。当接收到的回波信号相位变化率大于Th时,判断接收到的回波为体目标回波;当接收到的回波信号相位变化率小于Th时,判断接收到的回波为点源合成目标回波。特别地,在真实对抗条件下,只能获取有限方位角度下的回波数据,此时可根据获取的方位信息调整门限。

图24 基于相位变化率的体目标与双点源合成回波的分辨Fig.24 Discrimination between the real underwater target and the synthetic point-source echo based on phase change rate

5 结论

1)声信号从体目标正横方位入射时,体目标回波的频域相位变化率相对小;声信号从体目标艏艉方位入射时,体目标回波的频域相位变化率相对大,且量值差异明显;多点源合成目标回波相位变化率的这一特点不如体目标显著。

2)体目标回波相位变化率与多点源合成目标回波相位变化率在入射角90°附近量值差异较小,在其他角度下存在明显的量值差异。表明了通过对比两类目标回波信号相位变化率,可以对两类目标的回波进行分辨,同时验证了基于相位变化率的体目标与多点源和合成目标回波分辨方法的可行性。

3)需要说明的是,在水下体目标回波的仿真预报过程中,未考虑混响等干扰因素的影响,这是造成仿真预报结果与实验数据分析处理结果存在较大差异的主要原因,在后续的研究中将逐渐修正完善。