新高考中的概率与统计问题常见题型及处理策略

郭兴甫

概率与统计是高中数学教材中的重要内容，也是高考的必考内容和高频考点．随着新高考的全面实施，新高考对概率与统计的考查提高了要求，加大考查的力度和难度．为帮助读者更好地掌握新高考中概率与统计的常见问题，本文以近年各地的模拟题为例说明其常见题型及处理策略．

１ 频率分布直方图与方案选择综合问题

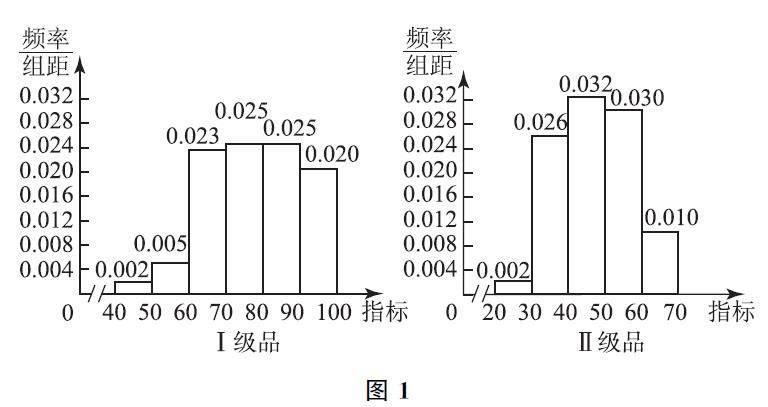
例１ 已知一芯片生产商用光刻机生产的Q 型芯片经过十项指标全面检测后，分为Ⅰ级和Ⅱ级，两种芯片的某项指标的频率分布如图１所示．

若只利用该指标制订一个标准，需要确定临界值c，将该指标大于c 的产品应用于A 型手机，小于或等于c 的产品应用于B 型手机．假设数据在组内均匀分布，以事件发生的频率作为相应事件发生的概率．

（１）求Q 型芯片Ⅰ 级品该项指标的第７０ 百分位数;

（２）当临界值c＝６５时，求Q 型芯片Ⅱ级品应用于A 型手机的概率;

（３）已知c∈[５０，６０]，现有足够多的Q 型芯片Ⅰ级品、Ⅱ级品，分别应用于A 型手机、B 型手机各１万部的生产．

方案１：直接将Q 型芯片Ⅰ级品应用于A 型手机，其中该指标小于或等于临界值c 的芯片会导致芯片生产商每部手机损失７００元;直接将Q 型芯片Ⅱ级品应用于B 型手機，其中该指标大于临界值c 的芯片，会导致芯片生产商每部手机损失３００元．

方案２：重新检测Q 型芯片Ⅰ级品、Ⅱ级品，可以避免方案１的损失费用，但检测费用共需要１０１万元．

请从芯片生产商的成本考虑，选择合理的方案．

解析

（１）设Q 型芯片Ⅰ级品该项指标的第７０百分位数为a，该指标在８０ 以下的概率为０５５，该指标在９０以下的概率为０８，因此该项指标的第７０百分位数a 一定在[８０，９０）内，所以０００２×１０＋０００５×１０＋００２３×１０＋００２５×１０＋００２５×（a－８０）＝０７（也可以用００２×１０＋００２５×（９０－a）＝１－０７），解得a＝８６，所以Q 型芯片Ⅰ级品该项指标的第７０百分位数为８６．

（２）当临界值c＝６５时，Q 型芯片Ⅱ级品应用于A 型手机的概率为００１×（７０－６５）＝００５．

（３）设直接将Q 型芯片Ⅰ级品、Ⅱ级品应用于A型、B 型手机时，该芯片生产商支出为y 万元，则

y ＝７００× [０００２×１０＋０００５× （c－５０）]＋３００× [００１×１０＋００３× （６０－c）]＝４０９－５５c（c ∈ [５０，６０]）．

当５０≤c＜５６时，y ＞１０１;当c＝５６时，y ＝１０１;当５６＜c≤６０时，y＜１０１．

综上，为降低芯片生产商的成本，当临界值c∈[５０，５６）时，选择方案２;当临界值c＝５６时，选择方案１和方案２ 均可;当临界值c∈（５６，６０]时，选择方案１．

点评

求解频率分布直方图与方案选择综合问题的关键：准确将题中所涉及的事件进行分解，明确所求问题所属的事件类型，弄清题意，特别地，要注意挖掘频率分布直方图中的数据条件．

２ 频率分布直方图与分布列的综合问题

例２ 为提高人民幸福指数，国家先后出台了多项减税增效政策．某地区对在职员工进行了个人所得税（以下简称个税）的调查，经过分层随机抽样，获得５００位在职员工的年个税（单位：百元）数据，按[０，２]，（２，４]，（４，６]，（６，８]，（８，１０]，（１０，１２]，（１２，１４]，（１４，１６]，（１６，１８]分成九组，制成如图２所示的频率分布直方图，假设每个组内的数据是均匀分布的．