巧借正交分解法解决高中物理力学难题

纪顺田

摘 要：力学是高中物理的重要知识点板块.在学习力学的过程中，我们不可避免地需要对受力物体进行受力分析，此时，我们就可以借助正交分解法将复杂的力逐步分解.所谓正交分解法就是指将力分解成水平和竖直方向的分力，结合受力物体的状态研究分力，解决问题.掌握正交分解法可以极大化地简化力学问题，提高同学们的解题效率和解题正确率.

关键词：高中物理；正交分解法；力学；受力分析

中图分类号：G632   文献标识码：A   文章编号：1008-0333（2024）07-0118-03

要想正确使用正交分解法，就需要先掌握正交分解法的原理及使用步骤.我们在利用正交分解法解决力学问题时，首先需要建立平面直角坐标系，找准受力物体水平和竖直方向的力，并将其分解[1].再结合已知条件和未知问题灵活把握，综合求解，不能做无用功，浪费时间.

1 如何构建平面直角坐标系

平面直角坐标系，顾名思义，需要在水平面上搭建.但是，在很多物理问题中，受力物体往往垂直于水平面或倾斜于水平面.那针对这些问题，我们又应该如何构建平面直角坐标系呢？下面，笔者就以具体例题为例，谈谈构建平面直角坐标系的方法：

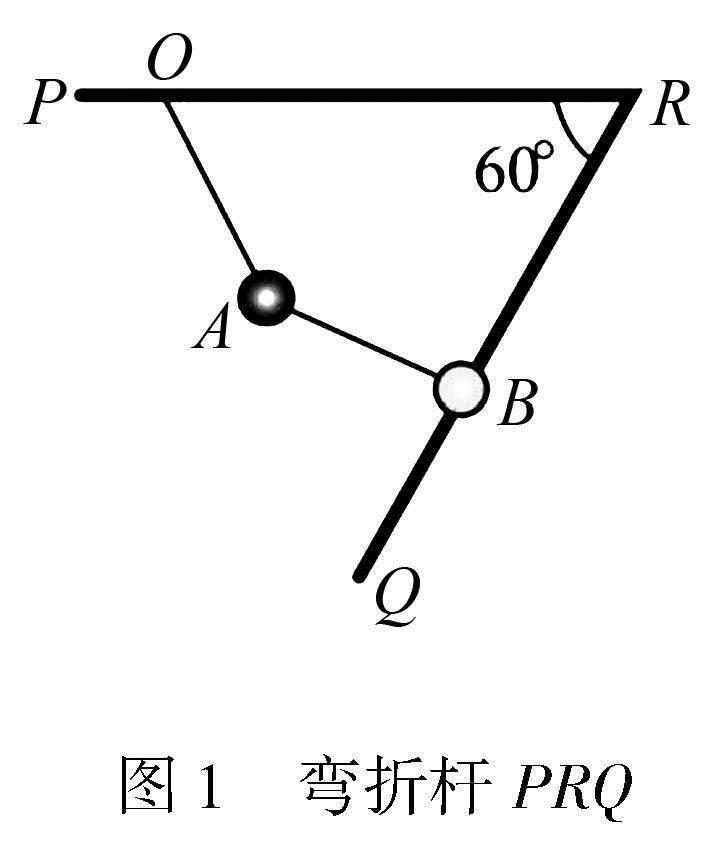
例1 如图1所示，弯折杆PRQ固定在竖直面内，PR水平，QR与PR间的夹角为60°，B球套在杆QR上，一根细线连接A、B两球，另一根细线连接小球A与杆PR上的O点，连接在O点的细线与水平方向的夹角为60°，连接A、B两球的细线与QR杆垂直，B球刚好不下滑.已知A球质量为2m，B球质量为m，两小球均可视为质点，最大静摩擦力等于滑动摩擦力，则小球B与杆QR间的动摩擦因数为（  ）.

解析 设连接O点的细线拉力为F1，连接小球B的细线拉力为F2，对A球研究，受力分析如图2：

构建完平面直角坐标系后，我们再开始分解F1和F2：竖直方向上：F1cos30°=2mg+F2cos60°水平方向上：F1sin30°=F2sin60°

解之：F2=2mg

对B球研究有：mgsin60°=μ（F2-mgcos60°）

2 使用正交分解法的步骤

（1）先对受力对象进行受力分析，画出受力图.需要引起同学们注意的是，有时一个题目中会有两个受力对象，这种情况下，学生就要根据题设条件和未知数灵活分析；

（2）以力的作用点为原点，建立平面直角坐标系；

（3）将不在坐标系上的力沿水平方向或竖直方向分解；

（4）将相同方向上的分力合并起来，一起计算并列出方程；

（5）求出合力的大小和方向.

例2 如图3，水平面上放置的是一个表面光滑的半圆柱体，将小球A置于该圆柱体上，并用水平轻弹簧拉住小球B，两小球A、B通过光滑滑轮用轻质细线相连，两球均处于静止状态.若B球质量为m，O在圆心O1的正上方，OA与竖直方向成30°，OA的长度与半圆柱体半径相等，OB与竖直方向成45°角，重力加速度为g，要求：

（1）绳OB拉力FTOB和弹簧拉力F；

（2）A球的质量mA.

3 正交分解法的具体应用

3.1 求合力

若物体受到多个力，采用常规的求合力方法难以突破时，我们可以采取正交分解法[2].将物体在同一平面不同方向上的作用力设为F1、F2、F3、F4….Fn，则我们建立直角坐标系xOy，并将这n个作

（1）若轻绳与水平面的夹角θ为60°，轻绳对石墩的总作用力大小；

（2）轻绳与水平面的夹角为多大时，轻绳对石墩的总作用力最小，并求出该值.

解析 （1）本题要求合力，故我们先对石墩受力分析可知：

Fcos60°=μ（mg-Fsin60°）

则当θ=60°时F最小，最小值为750 N.

3.2 受力平衡

若物体受到三个或三个以上的作用力，且处于平衡状态，则我们可以采用正交分解法進行解题，不仅能提高解题速度，而且能提高解题正确率[3].假设一个物体受到了n个不同方向上的作用力，且处于平衡状态，则我们先建立直角坐标系xOy，并将这些力分解到坐标轴上.根据物体处在平衡状态，合外力为0的规律，我们可以沿着水平方向和竖直方向，分别建立方程F1x+F2x+F3x+…+Fnx=0以及F1y+F2y+F3y+…+Fny=0，并以此求解.

A.FN>（M+m）g   B.FN<（M+m）g

C.f=0D.f≠0

3.3 受力不平衡

除了受力平衡外，正交分解法也常适用于受力不平衡的情况.当一个物体在受到n个作用力，但处于不平衡状态时，我们同样可以以该物体建立平面直角坐标系xOy，并将这个作用力分解到坐标轴上.则在水平和竖直方向上依据牛顿第二定律列出方程F1x+F2x+F3x+…+Fnx=max以及F1y+F2y+F3y+…+Fny=may，进而求解.

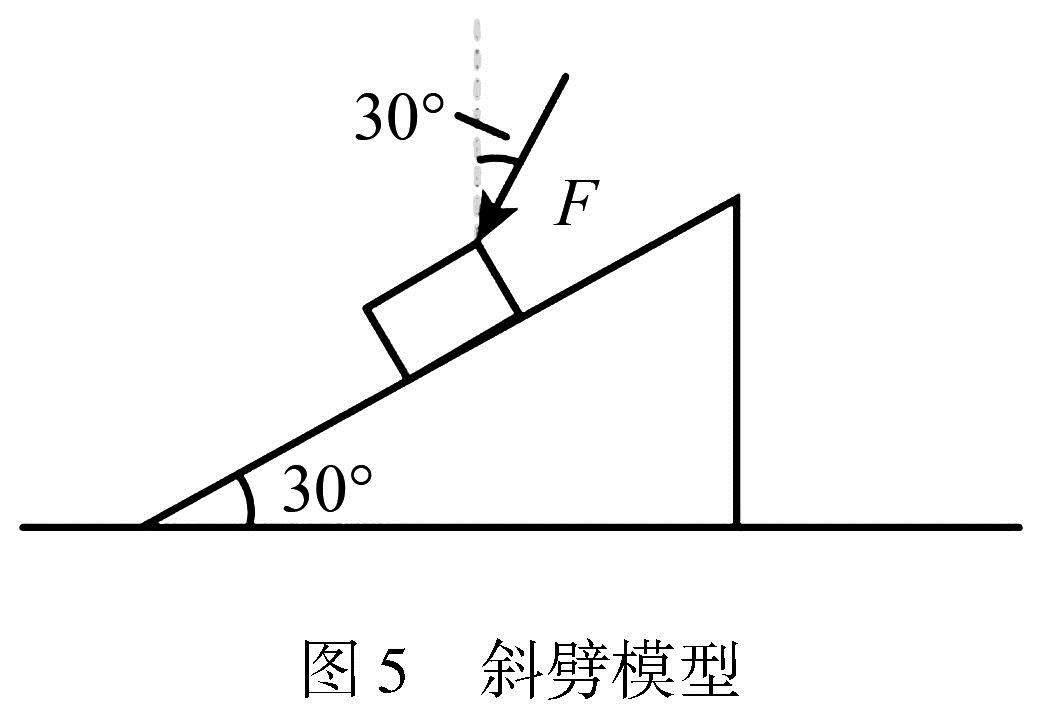
例5 若用弹簧测力计与水平方向成θ角斜拉木块，使其做匀速直线运动，如图6所示，求f与F的大小关系.若图中木块改为匀加速拉动，用木块质量m、拉力F、斜拉角度θ和加速度a表示木块和木板间的动摩擦因数μ.

解析 如图7，当物块匀速滑动时，则建立直角坐标系，结合平衡状态可得：

水平方向上：Fcosθ=f；

若木块改为匀加速拉动，则由牛顿第二定律Fcosθ-μ（mg-Fsinθ）=ma，

上述三种情况是常见的力学综合题型，也是正交分解法的适用范围.当然，除了力学外，正交分解法也可以用于计算位移、速度及加速度等矢量.

4 结束语

总的来说，正交分解法作为高中物理的重要知识点，同学们一定要重点掌握.在日常的训练和学习过程中也要培养自己使用正交分解法解决物理力学问题的意识.只有在日常学习中准确应用，及时总结，才能真正在考场上做到游刃有余.

参考文献：

［1］王一龙.正交分解法在高中物理中的巧妙运用[J].数理化解题研究， 2023（18）：74-76.

［2］ 陈建伟.正交分解法在高中物理解题中的应用[J].魅力中国，2019（2）：134-135.

［3］ 陈泽鲲.浅谈如何运用正交分解法解决力学问题[J].祖国，2019（1）：2.