双跨连续拱桥缆索吊装系统设计及计算分析
翁哲夫,郑 健
(1.广西新发展交通集团有限公司,广西 南宁 530029; 2.广西路桥工程集团有限公司,广西 南宁 530200)
1 工程背景
某桥主桥采用上承式双跨连续拱桥方案,为世界在建跨径最大的双跨连续拱桥。大桥单拱计算跨径380 m,矢高80 m,矢跨比1/4.75,拱轴线采用悬链线,拱轴系数1.55。
主拱桁采用钢管混凝土变高度空间桁架,四肢格构结构,断面高度从拱顶6.5 m变化到拱脚11.0 m,单侧拱桁宽7.5 m。两幅拱桁横向中心距17.5 m。单幅拱桁弦管由4肢φ1 400 mm钢管组成,上弦管自拱脚至拱顶壁厚分为35 mm,32 mm;下弦管自拱脚至拱顶壁厚分为35 mm,32 mm,28 mm。弦管对接接头采用内法兰盘栓接、管外焊接的形式进行连接。管内灌注C70自密实微膨胀混凝土。大桥采用缆索吊装斜拉扣挂法施工,桥型布置如图1所示。

2 缆索吊装系统设计
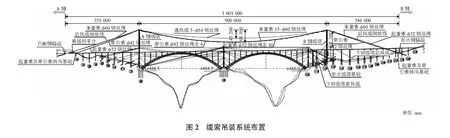
大桥缆索吊系统选用双塔三跨方案,吊装系统设计分主系统和工作索系统两种类型,每种类型均设计为两套独立系统。主系统跨径布置为355 m+900 m+350 m,单套系统设计吊重105 t,单个吊点最大吊重70 t,垂跨比1/14,主要用于主拱肋、拱上立柱及盖梁、桥面梁等安装,塔顶索鞍设计为可横移式,最大横移距离17.5 m;工作索跨径布置280 m+900 m+308.3 m,单套系统设计吊重10 t,垂跨比1/14,主要用于拱肋节段之间的风撑平联、剪刀撑等以及施工期间的小型机具、材料和构件的运输。受场地条件限制,边跨索布置呈外八字形式,最大偏角5°。大桥缆索吊装系统布置如图2所示。主要杆件统计见表1。

表1 主要杆件统计
3 有限元模型的建立
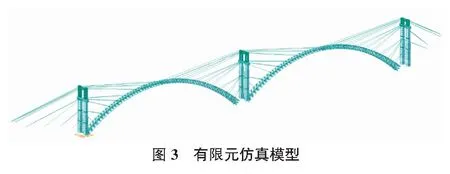
利用空间有限元程序MIDAS/civil 2019建立大桥拱肋吊装分析模型,拱肋吊装顺序按实际施工顺序模拟,拱肋容重按每节段实际吊重进行修正。大桥单拱半跨分8个节段安装,全桥共划分为64个吊装节段。大桥有限元模型如图3所示。
模型主要单元类型、材料名称以及截面形状尺寸如表1所示。
4 缆索吊装控制计算及结果分析
4.1 计算方法
对于钢管混凝土拱桥缆索吊装斜拉扣挂法施工而言,其关键在于拱肋扣索力和节段预抬量的求解。以“零弯矩法”为代表的解析法是CFST拱桥斜拉扣挂施工优化计算的重要方法[1],可以快速估算出结构施工过程中各扣索索力和各施工吊装阶段的预抬高值等,然而,由于该方法无法准确计算复杂桁式钢管混凝土拱肋的重心位置和计算长度等重要问题,因而计算精度较低。
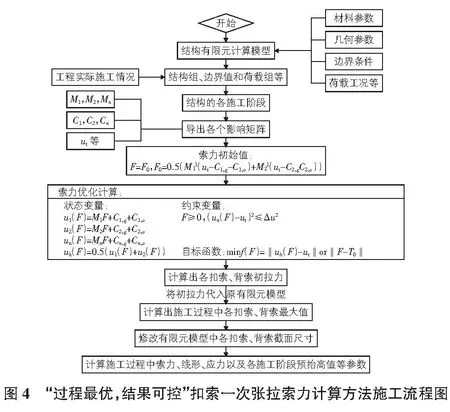
为克服传统计算方法计算效率低、精度差、过程烦琐等问题,秦大燕等[2]基于影响矩阵原理和最优化理论提出了“过程最优,结果可控”扣索一次张拉索力算法,本桥利用该方法进行缆索吊装施工控制计算,其详细计算流程如图4所示。
4.2 计算结果分析
以裸拱自重作用下的线形作为拱肋拆索后的目标线形,结合“过程最优,结果可控”一次张拉施工优化计算方法,获得实际施工过程中各施工阶段控制点位移和扣索索力。由于大桥整体结构对称,限于篇幅,仅提取单拱1/4肋拱肋线形和扣索张拉力计算结果,结果见图5,图6。

由图5可得,在整个缆索吊装施工历程中,拱肋线形变化较为平顺,拱肋松索后控制点线形与目标裸拱自重作用下线形偏差最大仅为19 mm,松索线形走势基本与目标线形一致,且在拱肋施工历程线形包络范围内波动较小,可见该组计算结果在施工过程中具有较高的安全性。
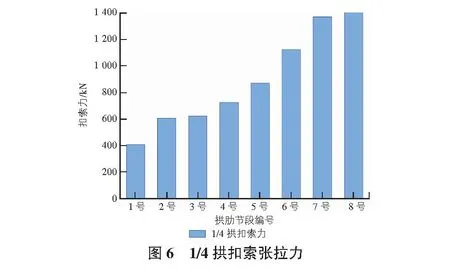
由图6可得,随着缆索吊装施工的进行,扣索力呈递增趋势,扣索力变化较为平稳[3],无剧烈突变,可用于指导施工。
根据MIDAS/civil计算结果,可得到各扣索在施工历程中的索力最大值,根据该值在考虑钢绞线2倍安全系数的基础上,进一步得到各扣索钢绞线配束,结果见表2。
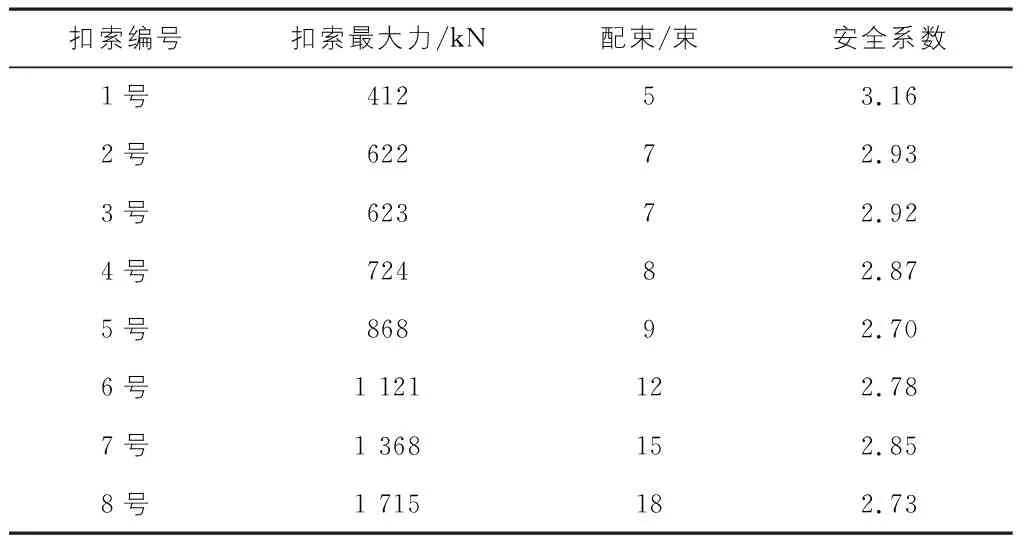
表2 扣索配束结果
4.3 实测结果对比分析
取上述分析位置单拱1/4肋松索成拱线形和扣索实际张拉力与计算结果进行对比分析,结果如图7,图8所示。
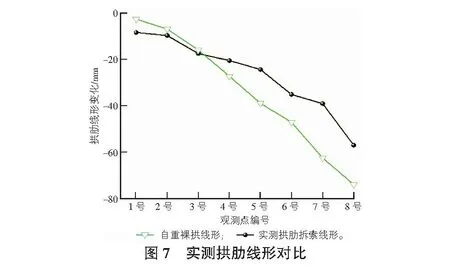
由图7可得,拱肋松索成拱后与目标线形最大偏差控制在24 mm内,满足JTG F80/1—2017公路工程质量检验评定标准中拱肋高程偏差(不大于L/3 000且不超过50 mm)要求[4],线形控制好。
由图8可得,就拱肋扣索力而言,实测索力张拉值与理论计算值最大误差控制在9%以内,过程无剧烈突变,可见扣索力计算精度较高。
5 结语
以某主跨2×405 m世界在建最大跨上承式双跨连续拱桥为工程背景,详细介绍了其缆索吊装系统设计并对其缆索吊装过程进行了仿真分析,得到如下结论:
1)考虑到现场实际情况,缆索吊装系统采用双塔三跨方案,主索和工作索系统单独设置,且均设计为两套系统。主索系统跨径布置为355 m+900 m+350 m,单套系统设计吊重为105 t;工作索系统跨径布置为280 m+900 m+308.3 m,单套系统设计吊重为10 t。
2)采用“过程最优,结果可控”一次张拉施工优化计算方法来计算扣索力、节段预抬量,可以达到很好控制拱圈线形的目的,可将成拱松索后拱圈线形与裸拱自重作用下的线形偏差控制在24 mm内,实际扣索张拉力与理论扣索张拉力最大误差控制在9%以内。