基于PCA算法的人脸匹配技术研究

冯 伟，杨春丽*，刘 峰，刘光宇,2，程 远，周 豹，赵恩铭，周维云，赵继强

（1.大理大学工程学院，云南 大理 671003；2.上海交通大学海洋智能装备与系统教育部实验室，上海 200030；3.中国人民解放军32268部队信息科，云南 大理 671003）

0 引言

随着人工智能的发展，身份信息的安全性和准确性变得尤为重要，人脸匹配由于其唯一性和不可复制性在信息安全问题上发挥了至关重要的作用［1］。人脸图像采集方式灵活、方便，通过手机、相机等设备就能随时完成人脸图像的采集［2］。在采集人脸图像时会受到噪声干扰，所以本文在加入不同程度噪声情况下完成人脸匹配。

人脸图像匹配的关键是人脸特征提取［3］。人脸面部细节的信息量特别大，人脸特征的提取比较困难。对于特征提取，一般有两种方法，第一种方法是根据人脸的几何特征，提取人脸图像器官几何特征；第二种方法是将人脸图像作为一个矩阵进行处理，对这个矩阵进行变换计算特征值和特征向量，特征向量即为“特征”。主成分分析法（Principal Component Analysis，PCA）属于上述的第二种方法［4］。它是一种数据降维方法，其设计思路是把m维的特征直接映射到k（k＜n）维上，这个k维特征是新的正交特征，全新构造得出的k维特征也被叫作主元，即为保留原数据最大的方向，此方向使数据的损失降到最低［5］，所以能有效地解决图像空间维数过高的问题，已经成为人脸匹配领域非常重要的理论。

基于PCA的人脸图像匹配技术，针对人脸特征进行面部特征提取，利用人特有的面部特征作为人脸匹配的依据［6］。由于周围环境的干扰，采集到的人脸图像可能存在噪声的干扰，所以对待匹配图像加入不同程度的高斯噪声，再用PCA方法完成人脸匹配，验证PCA人脸匹配的有效性。

1 基本原理和方法

1.1 数据预处理

在PCA人脸匹配中，数据处理的主要目的是减少特征之间的冗余性，降低维度，并提取有用的主成分，一般包括去中心化和归一化两个步骤［7］。

中心化是指将每个特征的值都减去对应特征的均值，使得所有样本点都以原点为中心。假设有n个样本数据和m个特征，则样本矩阵为

其中，xi∈Rm表示第i个数据样本，其各个特征为xij。则中心化矩阵为

归一化是指将每个特征都缩放到相同的比例范围内。由于采集到的人脸图像的各个特征的尺度可能存在差异，如果不进行归一化处理，则某些特征的重要性可能由于其数值范围较大而被过度强调，影响分类器的性能。如果对人脸的所有特征都单独分析，不严谨地降低指标，就有可能会导致一些重要的信息数据丢失［8］。

在PCA人脸匹配中，通常采用的方法是将数据中的每个特征都除以对应特征的标准差，使得每个特征的方差为1。经过数据处理后，可降低维度，提取主成分，并更好地反映原始数据的本质特征，有助于人脸匹配的准确率。PCA的核心理念就是对图像所涵盖的数据进行分析，进而提取利用价值较高的部分，这部分信息能很好地体现原人脸图像的特征，几乎不损失原图的主要特征信息，而且这几个信息之间一般不存在关联，可通过它们对原人脸图像进行描述，应用此类方法能够将有效信息得以保留并实现数据降维［9］。

1.2 协方差矩阵计算和特征分解

假设有N幅人脸图像用于训练，M幅人脸图像用于测试，把分辨率为m×n的图像按照每列相互连接，组成H=m×n维的列向量。整个人脸库用于训练的图像便构成一个矩阵KH×N，在N幅中的第i张图像存储在矩阵KH×N的第i列。同理可得测试样本矩阵，便可得出用于训练的样本平均值Xave：

根据用于训练的人脸图像与平均脸的方差构成协方差矩阵：

在获取人脸图像的特征脸时，可首先通过计算得出其特征值，然后按照特征值大小顺序依次排序，并从中选择前k个特征值，最后按照顺序获得对应的特征向量。这些特征向量就构成了特征子空间矩阵，也就是特征脸［10］。

1.3 维度空间转化

原来基于原始数据构成的空间称之为测量空间。进行分类以及匹配的空间称之为特征空间。对于特征空间来说，其中的每一个样本都可以通过向量的方式来表示，其本质含义就是空间中的点。PCA算法的主要原理是高维空间的数据投影到低维的特征空间中，用几个重要特征信息来表示原始的信息［11］。向量投影过程如图1所示。

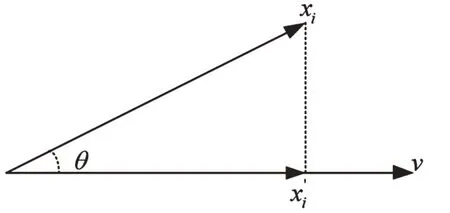
图1 向量投影图

具体投影过程的推导如下：

向量xi在v方向上的投影为x'i，其数学表达式为

在（6）式中θ是xi与x'i的夹角，两向量之间的内积表示为

因此有

然而坐标系中内积可以用（9）表示：

vT·xi可以用来表示投影后的数值大小。因此沿着某一特征分布的数值中，若该方向的方差越大，其表示该方向上的信息越充实，即主成分的特征越多。用（9）表示投影得数值大小，然后计算投影后的方差。假如数据已经标准化，有vT·x=0。对投影后得方差进行推导，结果为

又因||v||=vTv，则（11）式变换为

求（12）式的最大值，运用拉格朗日乘子法将（12）式推导转换为（13）式：

其中，f（v，λ）的平稳点与（12）式中的最大方差问题是等价的，对（13）求导得：

转换推导，将（14）方程等价于：

其中，Cv=λv就是求特征值和特征向量的方程，再回到求最大方差问题：

在（15）式的推导中，要求的方差是我们所求的特征值，只要把Cv=λv的特征值计算出来，再对特征值按从小到大的顺序进行排列，选择几个最大特征值，并求出特征值对应的特征向量，用这几个特征向量来完成数据集在方向上的投影［12］。

PCA 算法原理是先将向量xi在v方向上的投影为x'i，其次计算xi与v的内积，用vT·xi表示数值大小；再计算投影后的方差，并求出特征值和特征向量；最后对特征值进行排列，选取几个最大的特征值，求出特征值所对应的特征向量，这些特征向量就是数据集在v方向上的投影［13］。

1.4 相似度检测

在得到特征空间后，系统还无法对人脸图像进行匹配，还需要对投影到特征空间的向量进行计算。基于PCA 的人脸匹配方法通常利用距离函数作为最近邻法分类器对人脸图像进行分类［14］。最近邻法分类器的原理是将待匹配人脸图像和预存人脸图像投影到特征空间后，计算出特征空间中待匹配人脸图像和预存人脸图像间的距离，从而选择距离最小的待匹配图像作为匹配结果。距离有欧式距离、明式距离、绝对值距离和马氏距离，本文采用的是欧式距离。欧式距离公式为

其中，d（x，y）表示距离；x表示一个测量样本的特征量；y表示一个训练样本的特征量。

2 基于PCA算法的人脸匹配

在众多人脸匹配方法中，PCA算法是应用最广泛和最经典的方法之一。人脸图像涵盖了大量的数据，特征维数处于较高的水平，所以计算量一般情况下相对较大。为了有效降低特征的表示维数，霍特林系统地探讨了利用PCA 算法进行特征维数降低的方法，这种方法的复杂性低，在当前应用较广，而且在降维方面能够体现优良的效果［15］。主成分都是初始变量构成的线性组合，并且不超过初始变量的总量和保留了初始变量的核心信息。

基于PCA算法的人脸匹配是先进行人脸采集，再将采集的人脸图像进行预处理，得到统一分辨率的人脸图像，然后将图像分为测试集和训练集，分别对测试集和训练集用PCA算法降低每张人脸图像特征的维数，以提高算法效率。将训练集和测试集投影到低维空间，得到对应的特征向量。对于每个测试样本，在训练集中用欧式距离找到最短距离，并作为人脸匹配的结果。基于PCA算法的人脸匹配流程如图2所示。

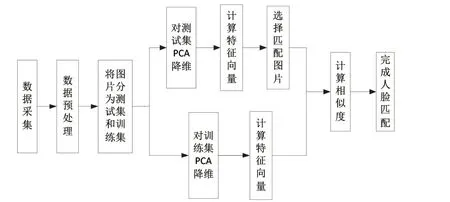
图2 PCA人脸匹配流程图

3 实验结果与分析

为了验证PCA人脸匹配的有效性，实验环境是在Intel（R）Core（TM）i7-8550U CPU @ 1.80GHz 1.99 GHz 的计算机软件Matlab2019b上进行。实验采集了20个人不同表情和角度拍摄的240张人脸图像，将其分为测试集和训练集，其中测试集有40张，训练集200张，每张图像为180*200的像素。图3是测试集中的人脸图像。

图3 测试集中人脸图像

实验可以任意选取测试集中任何一张照像作为待匹配人脸图像，实验以测试集中第1、第2张人脸图片为例，选取第1、第2张人脸图片在没有加噪声的情况下进行匹配，实验结果如图4、图5所示。

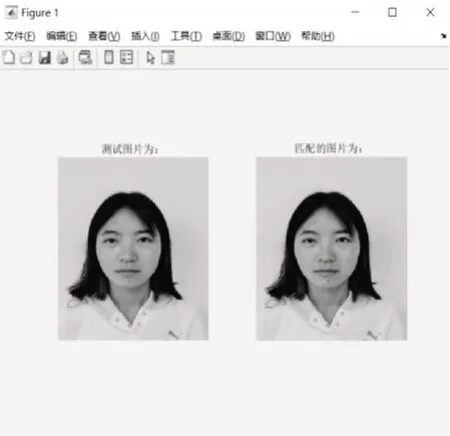
图4 第1张实验匹配

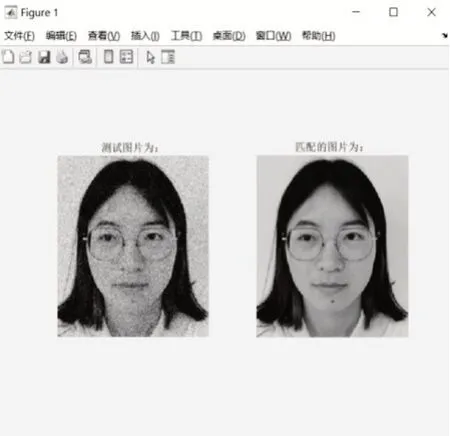
图5 第二张实验匹配结果

由于在采集和传输人脸图像时容易受到噪声的污染，所以本实验先对待匹配人脸图像加入不同程度噪声后再进行匹配，高斯噪声是自然界中最常见的噪声。为了验证PCA人脸匹配的抗噪性，对测试集中的所有人脸图像都加入方差为0.01的高斯噪声，具体测试集加噪结果如图6所示。

图6 加入0.01高斯噪声的测试集

对测试集中的图像加入方差为0.01 噪声不再进行人脸匹配，以测试集中第1、第2张人脸图像为列，实验结果如图7、图8所示。

图7 对第1张加噪声的结果

图8 对第2张加噪声的结果

对没有加入噪声和加入噪声的人脸图像进行匹配，完成人脸匹配时间和人脸匹配准确率测试，具体测试结果如表1所示。

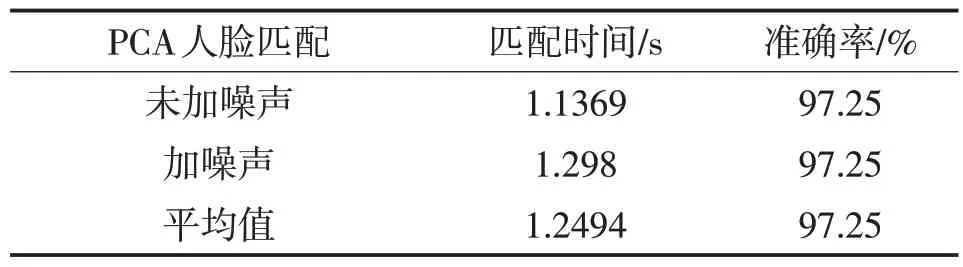
表1 匹配完成时间和准确率

通过实验验证PCA 人脸匹配方法能对人脸不同表情和加入较大噪声的情况下准确地完成人脸匹配，并能找到与测试图像最相似的训练图像作为匹配结果。实验结果显示基于PCA 算法的人脸匹配技术，加入噪声和未加入噪声的匹配准确率一致，说明PCA人脸匹配方法具有很好的抗噪性，平均完成时间为1.2494，匹配准确率为97.25%。

4 结语

本文采用了PCA方法完成人脸匹配，先将采集的人脸图像统一维度，然后经过数据处理，计算协方差矩阵，特征分解，投影到低维空间，最后匹配测试图像。实验结果显示，基于PCA的人脸匹配能准确完成人脸匹配，对不同角度拍摄和加入不同程度噪声的人脸图像能准确、快速地完成人脸匹配，抗噪性好，匹配结果非常准确。