逐步二型删失数据下广义Pareto分布的参数估计
苏燕青, 金良琼, 邹路燕, 李琼忆, 陶 永
(贵州民族大学 数据科学与信息工程学院, 贵州 贵阳 550025)
0 引言
在生存分析和可靠性分析中,存在寿命试验.生存分析中,研究对象在结束时间时发生了研究之外的其他事情,如疾病、拒绝访问或失去联系等,像这样无法明确地观察并且记录发生结束事件的生存时间的情况,试验通常会出现删失数据,而根据删失方式的不同,删失可以分为左删失、右删失、区间删失等.所以,对于删失情况的研究一直以来都受到众多学者的关注.Khorram等[1]在逐步二型删失的情况下,选择加权指数分布,针对加权指数分布的参数估计,利用近似极大似然估计和Bayes估计方法估计加权指数分布的参数,同时,使用Lindley近似方法得到贝叶斯估计的数值解形式.郭蕾[2]基于逐步二型删失数据,研究了广义指数分布的近似极大似然估计,运用Metropolis-Hasting算法模拟了广义指数分布在逐步二型删失数据下的贝叶斯估计.Alshenawy等[3]基于逐步二型删失数据,运用蒙特卡罗方法,估计了扩展奇威布尔指数分布的参数.鄢伟安等[4]讨论了Burr-XII分布在不同截尾试验下的极大似然估计和Bayes估计.Okasha等[5]讨论了在自适应I型渐近混合删失数据下威布尔分布的E-Bayes估计.El-Sherpieny等[6]推导了带有逐步二型截尾方案的似然函数,并将其应用于Clayton-BGR分布,得到了未知参数的渐近置信区间和自举置信区间.Pareto分布在经济上是描述收入的行为,特别是一些高收入个人的观察收入的理想模型,可以很好地反映财富分配状况,还可用于大额保险索赔的建模以及股票收益率预测.刘芹等[7]给出了Pareto分布参数的极大似然估计,分别在对称损失函数、二次损失函数、Mlinex损失函数下给出了参数的Bayes估计,对比了不同损失函数下参数的估计效果.蓝海等[8]基于不同的先验下,利用MCMC方法研究了反向帕累托分布形状参数的Bayes估计和E-Bayes估计.刘璐等[9]在定数截尾寿命试验场合下,运用轮廓似然函数法和枢轴量法研究三参数pareto分布参数的最优置信区间.本文在前人研究的基础上,对广义Pareto分布中尺度参数运用MCMC方法与Lindley近似方法进行了Bayes估计,同时,对尺度参数进行极大似然估计,对比了三种估计方法下的尺度参数的估计效果.
1 参数估计
1.1 模型描述
假设在一个寿命试验中,有N个试验样本,ti为样本的失效时间,样本xi是独立同分布的,并且xi服从广义Pareto分布,此时,观测到第一个试验样本的寿命时间后,从剩余的(N-1)个试验样本中随机抽掉r1个存活的试验样本,继续观察到第二个试验样本死亡,再从余下的(N-2-r1)个试验对象中随机抽取2个存活的试验样本不再进行观测.在这种方式中,按照事先安排的试验方案抽取,试验前确定的方案是(N,n,r1,r2,…,rn),把这种方案称为逐步二型删失试验.广义Pareto分布的概率密度函数和累积分布函数分别为:
f(x)=θβ(1+βx)-(θ+1),
(1)
F(x)=1-(1+βx)-θ,
(2)
其中θ与β分别为广义Pareto分布的形状参数和尺度参数,x≥0,θ>0,β>0.
假设(x1,x2,…,xn)是逐步二型删失试验中的试验样本,R=(R1,R2,…,Rn)是删失模式,当形状参数θ已知时,基于逐步二型删失模式下,试验个体的似然函数为
(3)
广义Pareto分布在逐步二型删失样本下的似然函数为:
(4)
其中
C=N(N-1-R1)…(N-n+1-
R1-R2-…-Rn-1).
1.2 极大似然估计
基于广义Pareto分布在逐步二型删失样本下的似然函数可推出广义Pareto分布在逐步二型删失样本下的对数似然函数为:
lnL(θ,β)=lnC+lnθn+lnβn-
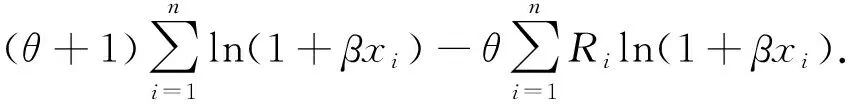
(5)
对对数似然函数中的尺度参数β求一阶导数,并令β关于对数似然函数的方程为0,即:
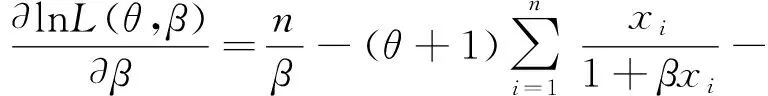
可得到β的极大似然估计值:
(6)
由于得到的尺度参数β的极大似然估计形式不能得到显示解,故考虑运用Newton-Raphson迭代法对尺度参数β的极大似然估计作参数估计.
1.3 贝叶斯估计
设{B1,B2,…,Bn,…}是样本空间Ω的一个完备事件群,即B1,B2,…,Bn,…相互之间是不包容的,A为Ω中的一个事件,且P(Bi)>0(i=1,2,…,n,…),如果P(A)>0,则有条件概率:
(7)
假设在试验中,每个试验个体都服从广义Pareto分布,在广义Pareto分布中,尺度参数β的先验分布β~Gamma(a,b),可以把尺度参数β的先验概率密度函数表示为:
(8)
尺度参数β的先验概率密度函数可写为:
π(β)∝βa-1e-bβ.
(9)
尺度参数β的联合后验密度函数为:
(10)
广义Pareto分布中,尺度参数β的联合后验密度函数正比于其似然函数与先验概率密度函数的乘积,所以广义Pareto分布尺度参数β在逐步二型删失数据下的联合后验密度函数为:
(11)
尺度参数β的Bayes估计为
(12)
基于上述两参数的后验密度表达形式,在贝叶斯估计中采用Metropolis-Hasting抽样算法对参数进行估计,具体算法如下:
(1)确定初始值β(0);
(2)令i=1;
(3)用Metropolis-Hasting方法从f(β|θ,β)产生样本β(i),这里的建议分布为exp(β(i-1));
(4)令i=i+1,重复步骤1-4共M次,生成样本β(1),β(2),…,β(M).
从公式(12)中得到的尺度参数β的Bayes估计的积分形式较为复杂,除了可以用Metropolis-Hasting抽样方法得到Bayes估计值外,另外一种方法如Lindley近似法也可以得到其后验分布的数值解,所以提出以下的Lindley近似法对其Bayes估计作简单的近似计算.
1.4 Lindley近似
Lindley近似法在1980年由英国统计学家Lindley提出,假设有参数β*,考虑如下的积分形式:
(13)
其中,β*=(β1,β2,…,βm),ω(β*)和v(β*)是关于参数β*的任意函数,l(β*)是关于参数β*的对数似然函数.
若π(β*)是参数β*的先验密度函数,且v(β*)=π(β*),ω(β*)=U(β*)π(β*),给定的x=(x1,x2,…,xn),U(β*)的后验期望为:
(14)
其中,ρ(β*)=lnπ(β*).
通过Lindley算法可以得到以下后验期望的近似表达式:

(15)
其中,
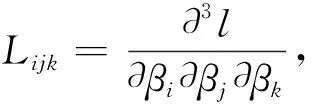
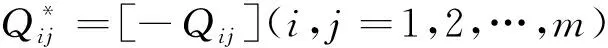
在广义Pareto分布中,固定广义Pareto分布中的形状参数θ为1,取尺度参数β=1,对尺度参数β作Bayes估计,其在平方损失函数下的后验分布的表达式比较复杂,除了用相应的Metropolis-Hasting算法对其进行后验抽样得到其Bayes估计外,还可以通过Lindley近似对其进行数值解得到相应的Bayes估计的数值解.本文主要研究的是广义Pareto分布中的尺度参数的估计,那么,基于平方损失函数下,尺度参数相应的Lindley近似可表示为:
(16)
其中,
u1=1,u11=0,
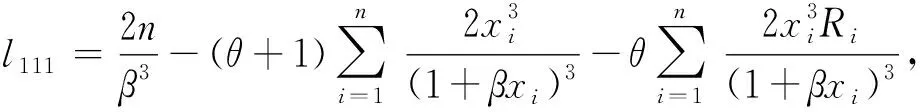
将相应的值代入式(16),可得广义Pareto分布在逐步二型删失数据下尺度参数β的Lindley近似结果.
2 数值模拟

得到的模拟结果如表1与表2所示.
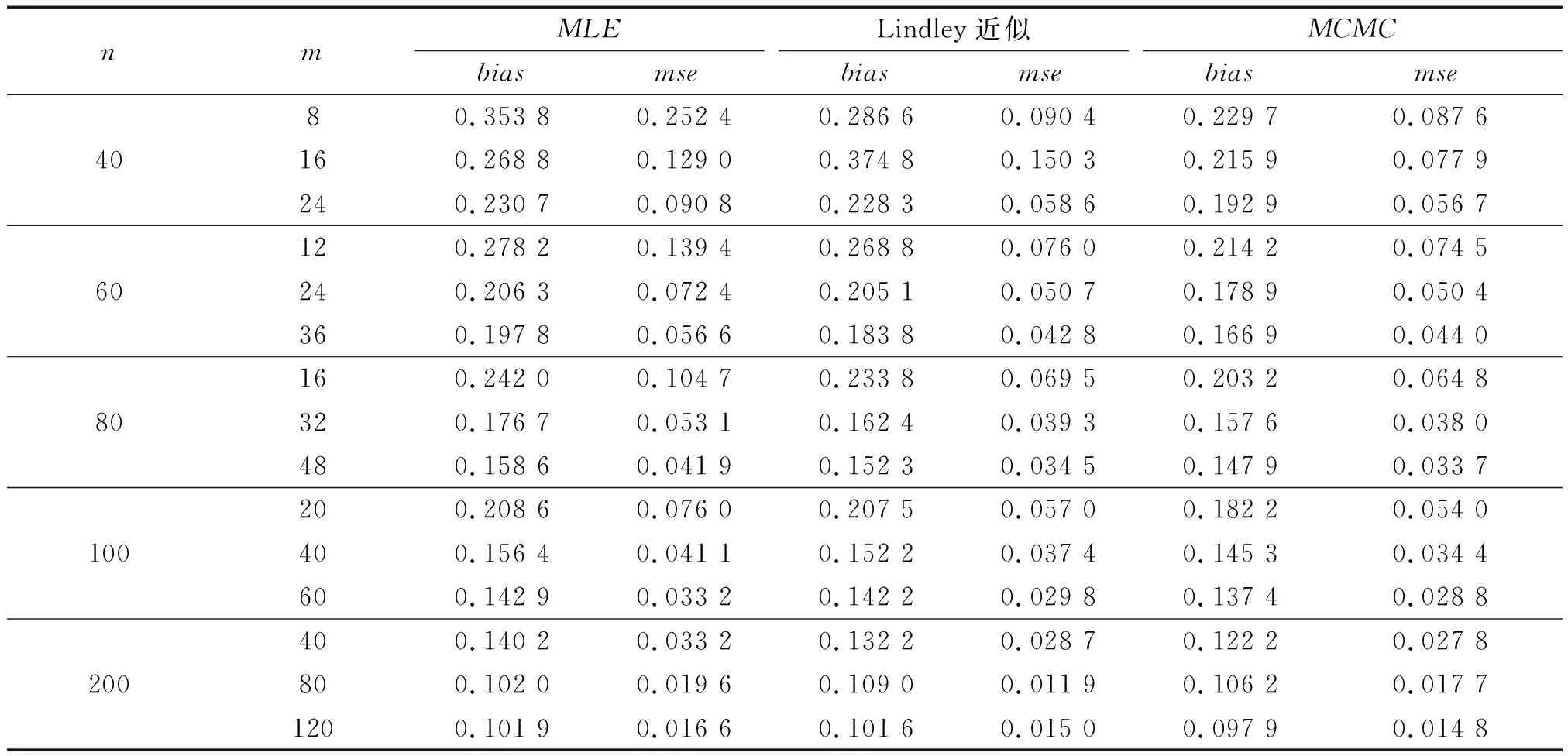
表1 删失机制1下MLE、MCMC、Lindley近似下的参数估计结果

表2 删失机制2下MLE、MCMC、Lindley近似下的参数估计结果
采用Metropolis-Hasting算法与Lindley近似法对广义Pareto分布的贝叶斯估计进行相应的数值模拟,结合β参数的极大似然估计,比较三种方法下的参数估计效果.同时,考虑如下两种删失机制:
删失机制1R1=R2=…=Rm-1=0,Rm=n-m.
删失机制2R1=n-m,R2=…=Rm=0.
相应的产生广义Pareto分布在逐步二型删失数据下的算法是由Balakrishnan等[11]提出,生成步骤如下:
(1)从均匀分布中产生n个样本g1,g2,…,gn;
(2)对于两种删失机制下给定的删失模式R1,R2,…,Rn,令
(3)让ui=(1-vnvn-1…vn-i+1),i=1,2,…,n;
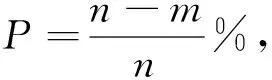
从表1与表 2得出如下结论:在相同的样本量时,广义Pareto分布中尺度参数β的平均偏差与均方误差随着删失机制的长度的增加而减小;在相同的删失率下,不同的样本量时,尺度参数β估计值的平均偏差与均方误差都随着样本量的增大而减小;在两种删失机制下,参数β的平均偏差与均方误差随着样本量的增大而逐渐减小;对比三种参数估计方法的效果,MCMC抽样>Lindley近似>极大似然估计.由于试验因素中存在的某些干扰因素,删失机制1中在样本量、删失机制的长度分别为40和16时,Lindley近似方法的估计效果稍差于极大似然估计方法的参数估计效果.
3 结论
在以上的数值模拟中,设定了两种形式的删失机制,分别对广义Pareto分布在逐步二型删失数据下的尺度参数进行了极大似然估计,使用了MCMC方法中的Metropolis-Hasting算法对参数在平方损失函数下的后验分布形式进行了抽样与使用Lindley近似算法得到了广义Pareto分布在逐步二型删失数据下的贝叶斯估计与贝叶斯估计的数值形式.从表 1与表 2中可以看出,固定了相同的样本量时,随着删失机制(R1,R2,…,Rm)中m的增加,参数β的均方误差与偏差在三种方法下的估计都在逐渐减小;在不同的样本量,在相同的删失比率下的删失机制中,参数β的均方误差与偏差在三种方法下的估计也在逐渐减小.从表1与表2中可以看出的总体情况为,基于两删失机制下参数估计中参数估计的样本容量在逐渐增大时,参数估计值的均方误差与偏差都在逐渐减小,对于MCMC的抽样方法,Lindley近似算法与极大似然估计方法下对参数β估计的效果.从表1与表2中看出,贝叶斯方法优于极大似然估计方法,贝叶斯估计方法中,MCMC方法优于极大似然估计方法.

