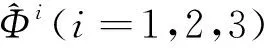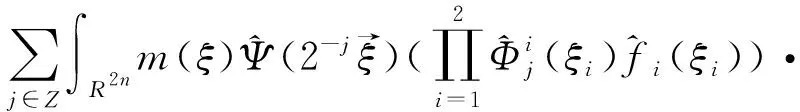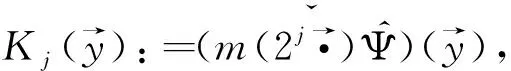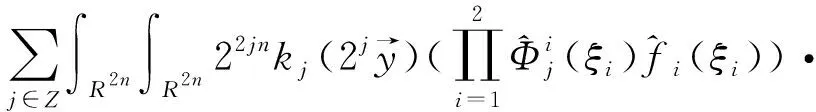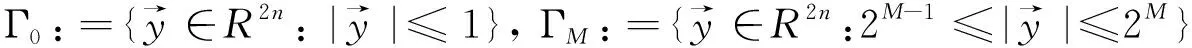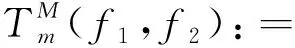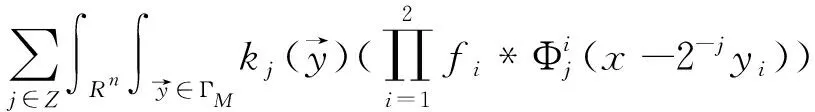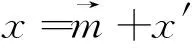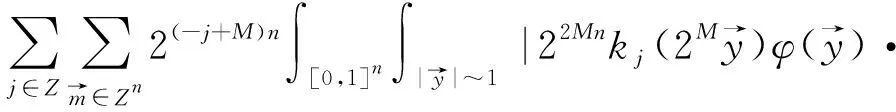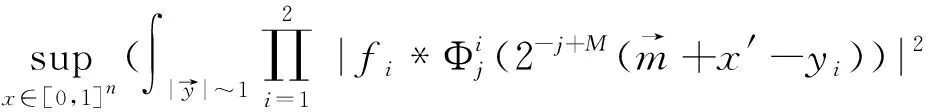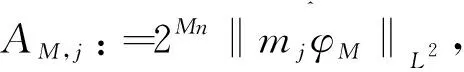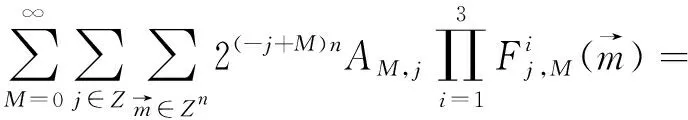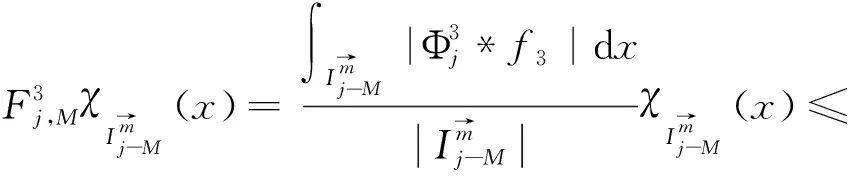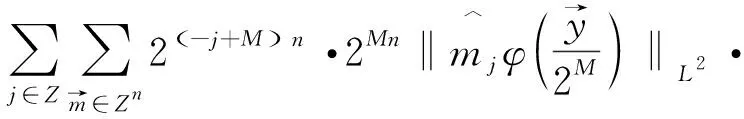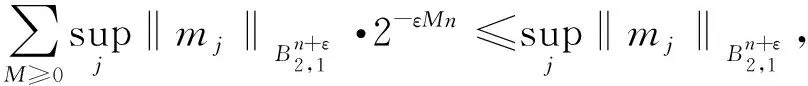带有Besov正则性的双线性乘子定理
张 子 梅
(重庆师范大学 数学科学学院, 重庆 401331)
1 研究背景
在介绍本文结论之前,先给出傅里叶乘子算子的定义:
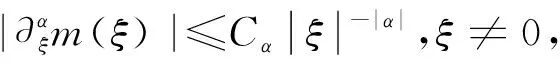
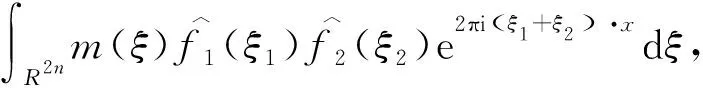
其中ξ=(ξ1,ξ2)∈R2n.

定理2[4]假设1 则得到 此外,Tomita[5]和Fujita等[6]也探讨了相关的带有Besov正则性的乘子算子的有界性,并且细化了对于乘子算子的研究.Grafakos等[7-8]则找到了乘子算子的Sobolev最佳指标以及局部光滑性对傅里叶乘子算子有界性的影响. 本文的主要工作是将傅里叶乘子算子的相关结论推广到Besov空间上,建立起带有Besov正则性的傅里叶乘子算子定理,并且延拓指标p的取值范围,得到关于该乘子算子有界性的最佳参数估计.对于定义在R2n上的有界函数m,定义其对应的乘子算子Tm如下 其中f1,f2均为定义在Rn上的Schwartz函数,ξ:=(ξ1,ξ2)∈(Rn)2,则dξ:=dξ1dξ2.本文主要结论可以归纳为以下的定理. 则有 ‖Tm‖Lp1(Rn)×Lp2(Rn)→Lp(R2n) 为了更加清楚地阐述结论,我们令ψ∈ζ(Rn)为一个Schwartz函数且满足以下关系 其中f∈ζ′(Rn). 在介绍两个重要的引理之前,给出关于Hardy-Littlewood极大函数的定义: 其中f为Rn上的局部可积函数,Q为Rn中包含x的任一方体.当0 ‖{Mr(fj)}j∈Z‖Lp‖{fj}j∈Z‖Lp. (1) 令φ和ϑ为定义在Rn上的Schwartz函数且满足 并定义φj:=2jnφ(2j·)和ϑj:=2jnϑ(2j·),则易得到以下估计 ‖{ϑj*f}j∈Z‖Lp(l2)‖f‖Lp(Rn), 除此之外,定义区间 在证明本文主要定理之前,先给出以下两个重要的引理及其证明. 和 其中M为任意常数. 通过以上过程,易得到关于第一个式子的有界性估计. 另一方面,第二个式子的研究过程为 以上引理得证. 自然地,考虑将以上引理从L2函数空间延拓到L1函数空间,也有类似的结论. 引理2令M≥0和1 和 其中M为任意数. 证明利用变量替换有 由不等式(1)以及Littlewood-Paley不等式,得 ‖ϑj*f‖L1(CI)χI(x)|I|·M(ϑj*f)(x). 则 ‖(|I|·M(ϑj*f)(x))‖Lp(Rn)‖f‖Lp(Rn), 结论得证. 在回顾基础知识和介绍了两个重要引理之后,给出本文主要结论的证明. 由此可定义一个三线性的算子UM为 且UM又可以改写为 接着将以上不等式分为两个部分讨论,其中一部分有以下关系成立 于是UM又可以重新写为 对于该不等式的右边分为三部分讨论,其中 结合之前的式子就转变为了 (1)p1>1,p2>1,p>1的情况. 根据引理1得到 同样地可以得到 根据以上信息有 综上所述,有 以上定理得证. 在说明结论之前,先给出Grafakos[10]提出的一个重要引理. 引理3令0 (1)‖f‖Lp,∞(Rn)≤A; (2)对于任意可测集E满足0<|E|<∞,当p′≤0满足1/p+1/p′=1,则存在一个子集E′⊆E满足|E′|≃|E|,且| 利用以上引理,就可得到关于本部分结论的重要证明. 证明给出一个可测集E使0<|E|<∞,f3=χE′且‖f1‖Lp1=‖f2‖Lp2=1,E′的取法可参考文献[10].由上面证明可知 其中ε≥0,由文献[10]可知 所以 得证.
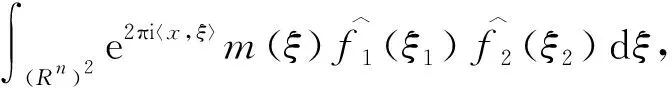
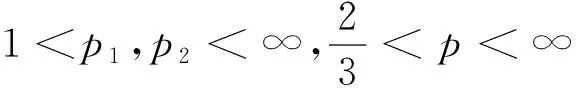
2 预备知识
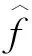

‖{φj*f}j∈Z‖Lp(l∞)‖f‖Lp(Rn).

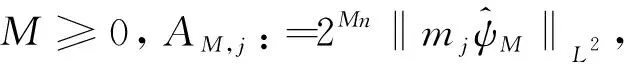
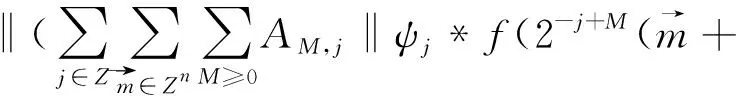
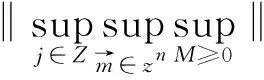
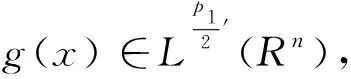

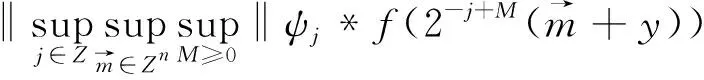
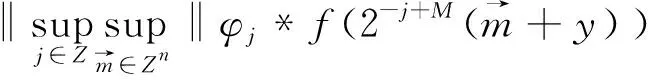

3 定理3的证明