M(P,Q)的一个小注

肖 丹 丹

(重庆师范大学 数学科学学院, 重庆 401331)

0 引言

设H是希尔伯特空间,B(H)为H上所有有界线性算子的空间．若算子P满足条件P=P*=P2,则算子P称为正交投影．P(H)表示B(H)上所有正交投影的全体,R(P)表示P的值域空间,N(P)表示P的零空间,N(Q)表示Q的零空间,R(Q)表示Q的值域空间．

两个投影算子理论是算子理论研究中的一个重要课题,其中M(P,Q)是研究P,Q的联合谱的最重要的工具之一．M(P,Q)是由Gehér等[1]研究Wigner定理在Grassmann空间上的改进时引进的,定义为:

目前已经有了M(P,Q)的一些相关研究[2-4]．Gehér等[1]证明了M(P,Q)的一些性质,并提出了一个问题:若P,Q∈B(H)是正交投影,则是否有

dimR(P)∩N(Q)=dimN(P)∩R(Q)

当且仅当M(P,Q)非空?Dou等[2]证明了以下内容:若P,Q∈P(H),

dimPH∩(I-Q)H=dimQH∩(I-P)H,

则M(P,Q)非空．Gehér等[3]得到R的一些相关性质:‖R-P‖≤sinθ,‖R-Q‖≤cosθ．他们利用M(P,Q)构造了Mθ(P,Q),Mθ(P,Q)被定义为如下形式:

Mθ(P,Q)={R∈B(H):R2=R*=R,
‖P-R‖≤sinθ,‖Q-R‖≤cosθ}．

当R(P)∩N(Q)非空时,

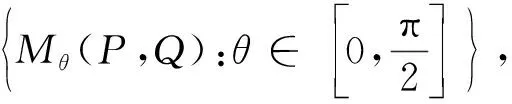
给出了从P到Q的测地线,并讨论

dim(PH∩(I-Q)H)=dim(QH∩(I-P)H)

与Mθ(P,Q)非空的关系．

本文需要的主要工具之一是著名的Halmos两个投影理论[5]．假设P,Q∈P(H),则H可以被分解为:H=H1⊕H2⊕H3⊕H4⊕H5⊕H6,则P,Q具有相应的矩阵表示:

其中T是H5上的正压缩算子,T的特征值不含0和1,V是从H6到H5的酉元,I是单位元．且

H1=PH∩(I-Q)H,H2=(I-P)H∩QH,
H3=PH∩QH,H4=(I-P)H∩(I-Q)H．

特别地,两个投影理论也常作为研究算子的联合谱的工具[6]．

本文将从两个引理出发,证明有关Mθ(P,Q)的一个定理．

1 Mθ(P,Q)的刻画

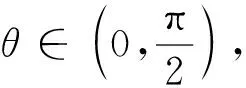
Mθ(P,Q)={R∈B(H):R2=R*=R,

‖P-R‖≤sinθ,‖Q-R‖≤cosθ}．

首先证明以下引理．

引理1若P,Q是B(H)上的投影算子,且

dim(PH∩(I-Q)H)=dim(QH∩(I-P)H)

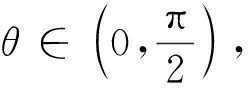
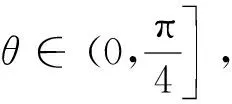
将H分解为:H=H1⊕H2⊕H3⊕H4,其中

H1=PH∩(I-Q)H,H3=PH⊖H1,
H2=QH∩(I-P)H,H4=(I-P)H⊖H2．

根据这个分解,P,Q可以写成如下形式:

其中V是H2和H3的酉元,T是B(H2)的正压缩算子．

注意到在H1⊕H2上,P,Q限制在H1⊕H2的形式为:

因为

dim(PH∩(I-Q)H)=dim(QH∩(I-P)H),

所以H1和H4是同构的．把H1和H4看作相同的空间,令R1在H1⊕H2上为

又因为

‖P1-R1‖2=sin2θ,‖Q1-R1‖2=cos2θ,

所以

‖P1-R1‖=sinθ,‖Q1-R1‖=cosθ．

在H3⊕H4上,因为V是酉元,H3和H4是同构的．在酉变换的意义下,改写P,Q限制在H3⊕H4上的形式如下:

令R2在H3⊕H4上为

同理可得,‖P2-R2‖=sinθ．

因为T是一个正压缩算子,所以可将T看作σ(T)上的连续函数,Q2可以看作

t→Q2(t):σ(T)→M2()

的一个连续映射,其中

R2:σ(T)→M2()

为一个常数映射,对任意t∈σ(T),

则对任意t∈σ(T)⊆[0,1],有

故

又因为

有

‖Q2(t)-R2(t)‖≤cosθ(t∈σ(T)),

所以‖Q-R‖≤cosθ．

综上所述,R就是所期望的投影:

下面,将证明另外一方面．

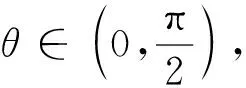
dim(PH∩(I-Q)H)=dim(QH∩(I-P)H)．

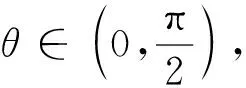
x∈K1=PH∩(I-Q)H,y∈K2=PH⊖K1,

w∈K4=QH∩(I-P)H,

z=K3=(I-P)H⊖K4．

因为R∈Mθ(P,Q),故

‖Rη‖=‖(P-Rη)‖≤sinθ,

(1)

‖(I-R)η‖=‖((I-Q)-(I-R))η‖≤cosθ．

(2)

另一方面,‖Rη‖2+‖(I-R)η‖2=1．由式(1)和式(2)可得,‖Rη‖=sinθ．因此〈Rη,η〉=‖Rη‖2=sin2θ,由于Rη=x+y+z+w,故

w=sin2θη+ξ,

(3)

其中ξ∈QH∩(I-P)H且ξ⊥η．注意到

‖PRη-Rη‖=‖-z-sin2θη-ξ‖=

以及

‖PRη-Rη‖≤‖P-R‖‖Rη‖=sin2θ．

由此可得z=ξ=0,故Rη=x+y+sin2θη．因此‖x+y‖2+sin4θ=‖Rη‖2=sin2θ,且

‖x+y‖=sinθcosθ,

(4)

注意到‖PRη‖≥‖Rη‖-‖Rη-PRη‖≥sinθ-sin2θ．

下面将证明QPRη=0．因为Rη=x+y+sin2θη,则

R(x+y-cos2θη)=0,

(5)

注意到

‖x+y-cos2θη‖2=‖x+y‖2+cos4θ=cos2θ．

因此‖x+y-cos2θη‖=cosθ．

另一方面,

Q(x+y-cos2θη)=Q(x+y)-cos2θη．

又因为

η∈QH,〈Q(x+y),η〉=〈x+y,η〉=0,

故

‖Q(x+y)-cos2θη‖≥cos2θ．

(6)

由式(5)可以得到,

‖Q(x+y)-cos2θη‖=
‖(Q-R)(x+y-cos2θη)‖≤
cosθ‖x+y-cos2θη‖=cos2θ．

(7)

比较式(6)和式(7),有

‖Q(x+y)-cos2θη‖=cos2θ,

因此Q(x+y)=0．则

QPRη=0,PRη∈PH∩(I-Q)H,

而且‖PRη‖≥sinθ-sin2θ．

综上所述,得到一个从QH∩(I-P)H→PH∩(I-Q)H的有界的线性的双射η→PRη．同理可以得到反过来的结论．因此

dim(QH∩(I-P)H)=dim(PH∩(I-Q)H)．

由引理1和引理2,可以得到以下的定理．

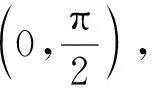
dim(QH∩(I-P)H)=dim(PH∩(I-Q)H)．

特别地,若

dim(QH∩(I-P)H)=dim(PH∩(I-Q)H)≠0,

则对任意R∈Mθ(P,Q),‖P-R‖=sinθ且‖Q-R‖=cosθ．