一类弱齐次向量优化问题解集的非空有界性
邹 萌, 李耿华
(重庆工商大学 数学与统计学院, 重庆 400067)
0 引言
弱齐次函数是Gowda等[1]在研究变分不等式问题时提出的一类新的函数,它是多项式函数的推广,近年来引起了众多学者的关注,并取得了一定的研究成果[1-4].解的存在性、稳定性及求解方法是优化问题和变分不等式的重要内容,许多文献对其进行了研究[5-6].由于渐近锥和渐近函数可以处理无界集合和函数,因而它们是优化问题及变分不等式解的存在性、有界性和稳定性研究的重要方法[7-18].
近年来,国内外学者利用渐近函数和正则性条件研究了多项式优化问题的解,并将其推广到了弱齐次优化问题.首先,Hieu等[10]利用多项式互补问题的正则性条件,证明了与多项式互补问题对应的优化问题的解集是非空紧的.随后,该学者在文献[11]中研究了多项式优化问题的正则性条件,并建立了非空闭集上该问题的Frank-Wolfe型定理和Eaves型定理.进一步地,Hieu[4]改进了文献[1-2]的弱齐次函数,并研究了相应的弱齐次优化问题解集的非空性和有界性.另一方面,Liu等[12]利用渐近函数定义了强型和弱型的正则性条件,并用其研究了多项式向量优化问题解的非空性、有界性和稳定性.
受文献[1,4,11-13]的启发,本文将研究文献[4]中的这一类弱齐次向量优化问题.首先,给出了该问题所对应的强型和弱型正则性条件,并研究其性质.其次,借助正则性条件,在函数没有凸性的假设下,研究了弱齐次向量优化问题的(弱)Pareto有效解集的非空性和有界性.此外,我们提出了该问题解集非空有界性的一个新的充分性条件,并讨论了它与强正则性条件的关系.
1 预备知识
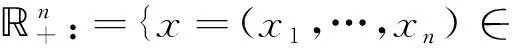
设f=(f1,…,fs):ns是向量值函数,K是n中的非空闭集,考虑如下向量优化问题:
首先,回顾向量优化问题几种解的定义,渐近锥、弱齐次函数的定义及相关性质.


注1显然,Ss(K,f)⊆Sw(K,f).当s=1时,VOP(K,f)退化为问题
OP(K,f):Minx∈Kf(x).
上述问题的解集记为S(K,f).
定义3[16]设K是n中的非空子集,K的渐近锥定义为
K∞:=
显然,K∞是闭锥;K有界当且仅当K∞={0};当K是非空闭凸集时,有K+K∞=K;特别地, ∅∞=∅.
定义4[4]设C是n中的一个闭锥,K是C中的一个无界闭集,h:C→是一个连续函数.如果对所有的x∈C和λ>0都有h(λx)=λrh(x),那么称h是r(≥0)阶正齐次的.若函数f:C→在K上满足f=g+h,其中h:C→是r阶正齐次的,g:C→是连续的.当x∈K且‖x‖→∞时,有g(x)=o(‖x‖r),则称f在K上是r阶弱齐次的h是f在K上的渐近齐次函数.
注2在上述定义中,渐近齐次函数h不一定是唯一的(参见文献[4]的例2.1).
本文主要研究弱齐次向量优化问题VOP(K,f),其中f=(f1,…,fs):ns在K上是连续的,且fi在K上是ri阶弱齐次的(i=1,…,s),h=(h1,…,hs)是f在K上的渐近齐次向量值函数.
下面,我们给出一个性质,说明f不同的渐近齐次向量函数在K∞上有相同的值.


hi(tkv)+gi(tkv)=fi(yk)=


下面介绍一个引理,它对研究问题VOP(K,f)的Pareto有效解的存在性具有重要作用.
引理1[20]设λ∈int和G(x0)={x∈K|fi(x)≤fi(x0),i=1,2,…,s}.若x′∈S(Gx0,g),则x′∈Ss(K,f).
接下来,讨论强型和弱型正则性条件的性质.


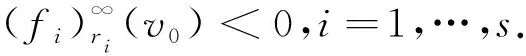

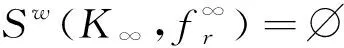



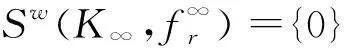

和
(1)

将上述不等式两边同时除以‖xk‖ri,当k→+∞时,有
(2)


注4性质2-4将文献[12]中多项式向量优化问题正则性条件的性质推广到了弱齐次向量优化问题中.
2 问题VOP(K,f)解集的非空性和有界性
本节旨在研究问题VOP(K,f)Pareto有效解集的非空性和弱Pareto有效解集的有界性.首先,给出了问题VOP(K,f)Pareto有效解存在的充分性条件.
定理1假设下列条件之一成立:
(ii)∃i0∈{1,…,s}使得
则Ss(K,f)是非空的.

fi(xk)≤fi(x0),∀i=1,…,s.
将上述不等式两边同时除以‖xk‖ri,当k→+∞时,有
(3)
显然,式(3)与
和
矛盾.故Gx0是紧的.由Weierstrass定理可知,S(Gx0,gλ)≠∅.由于S(Gx0,gλ)⊆Ss(K,f)(由引理1可得),所以Ss(K,f)≠∅.
注5定理1将文献[12]定理5.1的结论推广到了弱齐次向量优化问题中.此外,还提出了问题VOP(K,f)Pareto有效解存在的一个新的充分性条件(iii).

例1向量值函数f=(f1,f2),其中
K={(x1,x2)∈2|x2≥x1≥0}.
显然,
由于
{(x1,x2)∈K|x1=0,x2≥0}⊆SS(K,f),
故SS(K,f)是无界的.
下面,我们讨论问题VOP(K,f)弱Pareto有效解存在的必要性条件.


(4)

fi0(xk)-fi0(x0)≥0.

下面,我们将给出问题VOP(K,f)Pareto有效解存在性和弱Pareto有效解集有界性的一个充分性条件.


fiyk(y)-fiyk(yk)≥0.


由定理3和性质4(i)可得下述推论.

下面给出一个例子来说明定理3和推论1.
例2向量值函数f=(f1,f2),其中
K={(x1,x2)∈2|0≤x1-1≤3,x2-x1≥0}.

Ss(K,f)={(1,1)},
Sw(K,f)={(x1,x2)∈2|1≤x1≤4,x2=1},
故定理3和推论1成立.
下面,给出问题VOP(K,f)解集非空性与有界性的一个新的充分性条件,它比定理3中的条件弱.
定理4若函数f满足下列条件

则Ss(K,f)非空且Sw(K,f)有界.
证明由定理1可知,Ss(K,f)是非空的.下证有界性.我们先证明

(5)
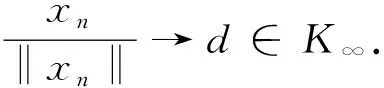
因此,式(5)成立.又因为Ss(K,f)≠∅,所以将式(5)结合条件(ii)可得,[Sw(K,f)]∞={0}.故Sw(K,f)是有界的.
注8定理4的条件(i)来源于文献[13].一方面,由性质4易知


最后,给出一个例子来说明定理4.

K={(x1,x2)∈2|x1≥1,1≤x2≤4}.

K∞={(x1,x2)∈2|x1≥0,x2=0},
因而
且

可知定理3条件不成立.
3 总结
本文研究一类目标函数是弱齐次的非凸向量优化问题.首先,给出了问题VOP(K,f)所对应的强型和弱型正则性条件,并研究其性质.随后,借助正则性条件,在函数没有凸性的假设下,研究了弱齐次向量优化问题的(弱)Pareto有效解集的非空性和有界性.此外,我们还提出了该问题解集非空有界性的一个新的充分性条件,并说明了该条件弱于定理3中的条件.

