基于相对利润最大化下的非对称量子Cournot博弈的动力学分析
邓 智 艺
(兰州交通大学 数理学院, 甘肃 兰州 730070)
0 引言
在传统经济学中,相对利润最大化是企业和个体在决策过程中的最终目标.然而,随着科技进步和市场竞争的不断发展,经济系统中的决策环境变得越来越复杂.为了更好地理解这种复杂性,研究者们开始将量子纠缠引入博弈模型,通过应用量子力学中的概念研究经济体中的决策行为和相互之间的联系.Meyer[1]通过掷硬币的模型,首次在经济模型中提出了量子博弈.随后,Eisert等[2]通过囚徒困境说明了在经典博弈模型中无法达到帕累托最优时,将量子纠缠引入可以达到帕累托最优.Li等[3]通过在连续策略空间中具有量子纠缠的Cournot博弈模型,提出了LDM(Li-Du-Massar)量子化方案,表明在引入量子纠缠之后,企业之间的决策不再是独立和相互对立的.随后,诸多学者开始应用量子方案来解决经济博弈的问题[4-8].量子博弈理论为我们提供了一种全新的视角,使我们能够更好地理解市场竞争、合作和战略决策的复杂性.
在实际经济系统中,需求函数和成本函数常常存在非对称性.不同企业或个体面临着不同的市场条件和资源约束,导致需求函数和成本函数之间存在差异.在Cournot博弈中,一个企业先行动,而其他企业根据该行动做出反应.这种非对称性对于博弈行为和策略选择产生重要影响,后续通过动力学分析来探索系统的演化和稳定性.
动力学分析是一种研究经济系统中随时间演化的行为和模式的方法.通过建立数学模型和动态方程,研究者们可以揭示经济系统中各个因素之间的相互作用和变化规律.Rand[9]首次将非线性动力系统与寡头垄断模型相结合,开辟了一条分析经济系统复杂性的新途径.Bischi等[10]则运用平面离散时间动力系统描述有界理性企业的双寡头博弈,深入研究了复杂的动力学现象和吸引盆的结构,并借助临界曲线探究了不可逆映射.另外,Liu等[11]应用不变集和横向Lyapunov指数研究了同步行为,并通过数值模拟探讨了吸引子共存条件下的吸引池.还有研究者关于博弈论与动力系统进行了其他领域的研究[12-14].这些研究为我们更好地理解经济系统中的复杂行为和动力学现象提供了重要的见解,也为经济学及相关领域未来的研究奠定了坚实基础.
本文通过建立有限理性下具有非对称需求函数以及成本函数的Cournot博弈模型,关注纳什均衡点处的局部稳定性,并探索参数对其影响.其次,研究不同参数下分岔引起的混沌现象,揭示在不同参数下企业量子决策的动态变化和系统行为.
1 模型建立
考虑一个双寡头Cournot模型,市场中的两家企业具有如下的逆需求函数:
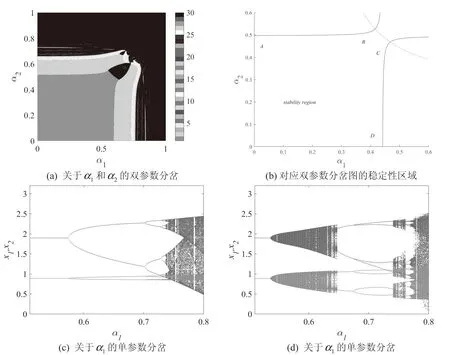
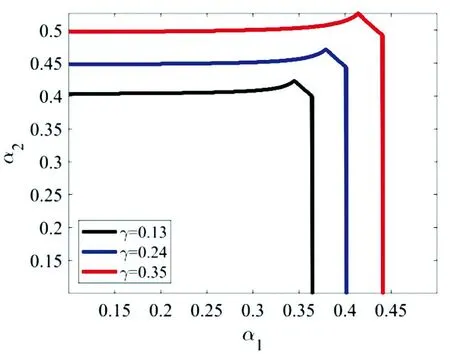
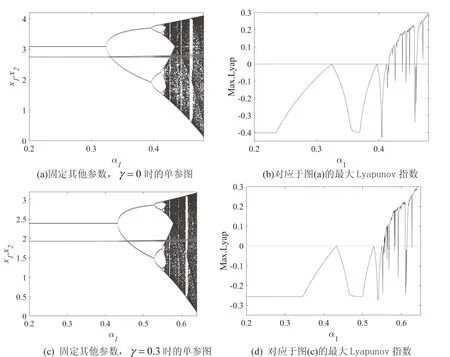
其中a>0表示产品被市场给出的最高价格,0 两家企业的成本函数为:Ci=ciqi,i=1,2,其中ci>0为边际成本.此时两个公司的绝对利润为: 两个公司的相对利润为: 其中,x1和x2分别代表企业1和企业2在市场中所采取的决策.从中可以发现,当γ≠0时,两个企业的决策不像经典博弈模型中那样是相互独立的情况,而是相互合作,两者发生纠缠的情况.而当γ=0,即两家企业不存在量子纠缠的情况下,量子博弈退化为经典博弈模型. 将量子纠缠引入经典博弈模型后,得到量子博弈模型的相对利润表达式为: 将上面企业1以及企业2的相对利润函数分别对x1和x2求偏导,可以得到相对边际利润为: 在实际情况中,企业在市场中无法获得全部的需求信息,所以假设企业采取有限理性期望,即根据上一个时期的边际相对利润来调整下一个时期的产量.这种调节机制可以用如下的方程表示: 根据上面的调节机制可以建立如下的动态博弈模型: (1) 其中α1>0,α2>0分别表示第一个企业和第二个企业的产量调节速度. 在模型(1)中,令xi(t+1)=xi(t),可以得到下式 (2) 根据式(2)可以得到系统的三个边界均衡点 以及唯一的纳什均衡点E*=(x*,y*). 令 其中A=2a-2c1-ab1+ab2+b1c2-b2c2,B=2a-2c2+ab1-ab2+b2c1-b1c1. 由于产量只有大于0在实际情况中才有意义,所以下面的分析是基于均衡点为正的情况下给出的.而边界均衡点表示市场中有一家企业的产量为0,这在实际情况中几乎是不可能的,对此研究没有什么意义.为了使研究更符合实际情况,对在纳什均衡点E*=(x*,y*)处的局部稳定性进行分析. 系统T在E*处对应的雅可比矩阵为: (3) 其中 为了便于分析,根据在纳什均衡点E*处有下式成立 (4) J(E*)= 则矩阵J(E*)的特征多项式可以表示为: P(λ)=λ2-Tr(JE*)λ+Det(JE*), 其中Tr(JE*)为雅可比矩阵J(E*)的迹,Det(JE*)为雅可比矩阵J(E*)的行列式,分别为: 根据非线性动力学的相关理论[15],可以用对应量子均衡点处的雅可比矩阵特征值的模与常数1的关系来分析该均衡点的局部稳定性.当|λ1|<1,|λ2|<1,此时量子均衡点是一个稳定的结点;当|λ1|>1,|λ2|>1,此时量子均衡点是一个不稳定的结点;若|λ1|<1,|λ2|>1或|λ1|>1,|λ2|<1,此时量子均衡点是一个鞍点.而矩阵J(E*)的特征值的表达式难以求解.根据Jury判据[16],当|Tr(J)|-1 (5) 由1-Tr(J)+Det(J)>0,知系统(1)在纳什均衡点处不会通过叉式分岔、折分岔或跨临界分岔失去稳定性.并据1+Tr(J)+Det(J)>0以及1-Det(J)>0,可得: (6) 当满足式(6)时,系统在E*处才是稳定的. 若采用对称的需求函数以及成本函数,即b1=b2=b,c1=c2=c时,系统(1)可化为: (7) (8) 由式(8)可知1-Tr(J)+Det(J)>0成立,剩下两个条件可化为: (9) P(λ)=λ2-Tr(J(E*))λ+Det(J(E*))=0, 在量子Cournot博弈离散动态系统中,涉及两家企业基于有限理性做出决策的产品产量博弈.这种博弈无法立即达到量子纳什均衡状态,需要经历多次重复博弈才能逐渐接近均衡状态.值得注意的是,量子纳什均衡是局部渐近稳定的,这意味着系统可能对任意参数的微小变化相对敏感.为了更深入地了解系统行为,利用数值模拟探究不同参数变化对量子Cournot博弈的影响.通过这种方法,可以更具体地了解企业间决策行为和产量博弈的演化过程.这将有助于揭示量子Cournot博弈的动态特性,并为制定决策策略提供有价值的见解.Zhu等[17]根据分岔图、最大Lyapunov指数图以及吸引盆分析了基于等弹性需求函数的量子博弈模型的动力学行为.本文采取类似的分析方法,探讨不同调整速率和量子纠缠下系统的动态演化. 本文将数值模拟中各参数无量纲化,得到基准值分别为a=6.0,b1=0.1,b2=0.2,c1=0.2,c2=0.2.采用双层迭代算法,得到当γ=0.3时,参数平面(α1,α2)的二维分岔(见图1(a))以及对应的稳定区域(见图1(b)),其中棕色区域表示周期1,浅绿色区域表示周期2,以此类推,超过30个周期的区域用黑色表示.在图1(b)中发现,若α2穿过曲线AB或CD,系统将经历Flip分岔;当α2穿过曲线BC时,系统将经历Neimark-sacker分岔.根据式(10),得到当调节速率的值取α1f以及α1NS时分别会发生Flip分岔和Neimark-Sacker分岔.并且从图1(b)中看出,当调整速率过大时,系统可能会陷入混沌状态.所以控制调节速率的值可以维持市场环境的相对稳定.当选取参数a=6.0,b1=0.1,b2=0.2,c1=0.6,c2=1.2,α2=0.5时,如图1(c)所示,此时系统会通过Flip分岔失去稳定性;而当α2取值增大到1.1时,如图1(d) 所示,此时系统通过Neimark-Sacker分岔失去稳定性. 图1 双参图及其对应的稳定性区域以及关于α1的单分岔图 (10) 图2展示了量子纳什均衡点在(α1,α2)平面内稳定区域的边界曲线.当固定参数a=6.0,b1=0.1,b2=0.2,c1=0.2,c2=0.2时,随着纠缠参数γ的增大,量子均衡点的稳定性区域将会增大.这种现象表明,当量子纠缠参数增大时,可以使市场和企业变得更稳定.这是因为纠缠参数的增加会导致企业之间的纠缠程度加深,使相关的量子系统之间的关联性更强.这种增强的关联性可以帮助企业更好地理解市场动态,提高决策的可预测性.因为纠缠现象本身具有一定的规律性,市场中的企业可以更准确地预测其他企业的行为或市场的未来走势,从而减少市场的不确定性. 图2 不同量子纠缠对应系统稳定域的边界曲线 固定参数a=6.0,b1=0.1,b2=0.2,c1=0.1,c2=0.2,α2=0.1,图3展示了关于参数α1的单参数分岔以及相对应的最大Lyapunov指数.从图3中可以发现,当纠缠系数γ增大之后,产量调整速度对市场的灵敏度减小,这意味着产量的变动对市场影响较小.同时,系统的稳定性增强,出现分岔和混沌的可能性较低.通过观察图3(b)以及图3(d)中的最大Lyapunov指数,我们可以验证之前的分析.当最大Lyapunov指数为负时,系统呈现稳定状态;当最大Lyapunov指数为零时,系统处于分岔点;而当最大Lyapunov指数为正时,系统进入混沌状态. 图3 纠缠程度对系统的影响 这种情况下,两个企业之间的量子纳什均衡产量可能会下降.这是由于纠缠度的增大导致企业间的相互影响变得更为复杂和强烈,从而影响了均衡产量的确定.纠缠度的增加可以改变博弈的动态特性,导致均衡产量向低调整. 需要注意的是,纠缠度对系统稳定性和均衡产量的影响是多方面的,受到其他因素的综合作用.纠缠度增大可以提高系统的稳定性、降低分岔和混沌的可能性,但在特定情况下,它也可能导致均衡产量的下降.这种复杂性要求我们在研究中要综合考虑各种因素,并基于具体情况进行分析和推断. 综上所述,随着纠缠度的增大,产量调整速度对市场产量的灵敏度减小,系统的稳定性增强,分岔和混沌的可能性减小.然而,这种情况下两个企业之间的量子纳什均衡产量可能会下降,因为受到纠缠度及其他因素的综合影响. 最后,分析采用对称的需求函数以及成本函数时的情况,即b1=b2=b,c1=c2=c.取a=6.0,b=0.1,c=0.2,γ=0.3,参数平面(α1,α2)的双参数分岔如图4(a)所示.从图4中可以观察到,此时系统只能通过Flip分岔进入混沌,图4(b)可以验证这种说法.并且,当采用对称的需求函数以及成本函数时,可以得到与前面一致的结论,即当企业以较小的调整速率来调整其产量时,可以使得市场环境保持相对稳定的情况. 图4 对称情况下的双参图以及关于α1的单分岔图 上述数值模拟验证了理论分析的结果,即当采用对称的需求函数以及成本函数时,系统只会通过Filp分岔失去稳定性.而根据前面的分析,当采用非对称的需求函数以及成本函数时,系统会通过Filp分岔和Neimark-Sacker分岔两条路径通向混沌. 吸引子共存现象是指在一个动力系统中同时存在多个稳定状态或周期性行为的现象,这些吸引子之间相互影响,并且可以通过调节系统参数来改变它们的相对稳定性.固定参数a=6.0,b1=0.1,b2=0.2,c1=0.1,c2=0.2,α2=0.6,γ=0.3(见图5).图5表明,当初值取在黄色区域中时,产生的轨迹会收敛于黑色4周期吸引子,而当初值取在绿色区域中时,产生的轨迹会收敛于红色4周期吸引子,蓝色区域为逃逸区域.从图5(a)到图5(b)可以发现,随着α1从0.527增加到0.534,黑色4周期吸引子变为8周期吸引子,并且黄色区域的面积逐渐增大.在经济学和市场中,吸引子共存现象被用来解释不同竞争策略的共存和相互影响.在市场竞争中,企业可以采取不同的策略,例如产量竞争、产品差异化或专注于特定市场细分.这些不同的竞争策略可以被视为不同的吸引子,它们在市场中共存并相互影响. 图5 共存吸引子及其吸引盆 针对现有研究领域单一的需求函数和成本函数以及研究对象多为静态模型的不足,本文提出了具有非对称需求函数以及成本函数的Cournot博弈模型,旨在深入研究经济系统中复杂行为和决策过程.通过引入量子纠缠,将之前独立的决策关系变为相互合作的决策关系.并基于有限理性调节机制建立了动态方程来描述企业之间的相互作用和策略选择的变化.通过分析这些动态方程,我们可以揭示系统中的平衡点、周期性行为以及稳定性的条件.动态分析揭示了系统的演化、稳定性和行为模式,为我们深入理解经济系统的动态行为和决策提供了有益的洞察,为经济决策者和政策制定者提供了有效的参考和指导.未来的研究可以进一步拓展这些概念,对经济系统中动态行为做出进一步说明.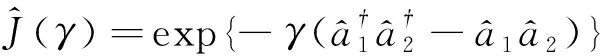
2 平衡点的局部稳定性

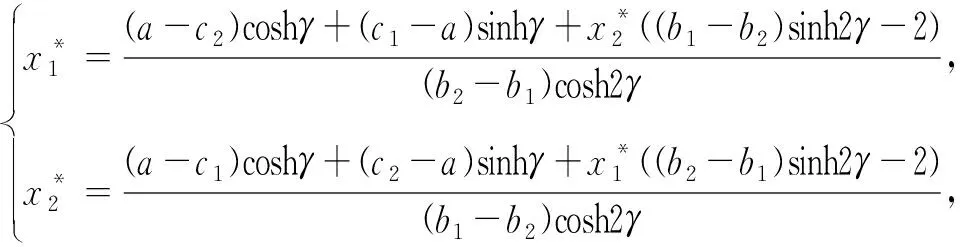
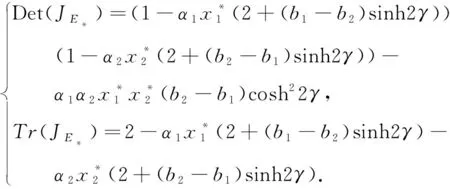
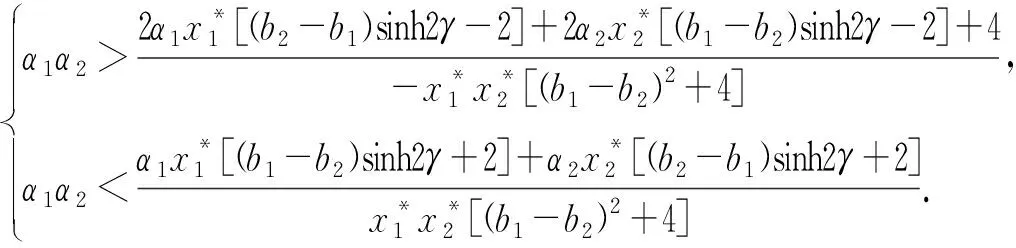

3 数值模拟


4 总结

