基于近场动力学方法的玻璃板冲击破坏数值模拟研究

李松波, 王志良, 申林方, 华 涛, 李 泽

(昆明理工大学 建筑工程学院,昆明 650500)

玻璃作为一种具有耐高温、耐腐蚀、强度高等优点的材料,在建筑、汽车、航空航天等重要领域得到广泛的应用。在建筑领域,玻璃材料应用于大型玻璃幕墙、天窗、隔断墙等,其强度和耐久性直接关系到建筑物的安全和舒适度[1]。在汽车领域,玻璃是车窗和车灯等结构的必备部件,其质量和强度对车辆的安全性能至关重要[2]。在航空航天领域,航空仪器和航天器中使用了大量玻璃材料,其性能直接影响着飞行安全和任务成功[3]。因此,针对玻璃材料在冲击荷载作用下的失效机理及破坏形态展开研究,具有重要的理论和工程应用价值。

目前,国内外学者关于冲击荷载作用下玻璃板的破坏机理及损伤形态已开展了大量的研究工作,并在理论分析、试验研究及数值模拟等方面,取得了丰硕的研究成果。在理论分析方面,研究人员基于极限状态设计理论、断裂力学理论、疲劳失效理论、可靠性理论等,提出了多种描述玻璃失效的准则和概率模型,如:最大主应力准则、最大切应力准则、应力强度因子准则等。如:Shand[4]认为玻璃裂纹孕育起源于局部应力超过某一最小值,且裂纹扩展速率随裂纹的增长而增加。姚国文等[5]提出了一种由偏应力冲量决定的损伤累积模型,并采用Heaviside 函数来描述材料内部的破坏迟滞现象。Pyttel等[6]提出了一种夹层玻璃在冲击载荷作用下的失效准则,并认为玻璃在发生失效前必须达到临界能量阈值。高轩能等[7]基于爆炸冲击波传播特性与玻璃强度理论,提出了建筑玻璃的爆炸冲击破坏准则,并分析了框支承玻璃在爆炸冲击波作用下的安全距离。然而,这些准则和模型均需要在一定假设的前提进行简化计算,与玻璃冲击破坏的实际情况往往存在较大误差。试验研究作为最可靠和直观的方法,在评估玻璃抗冲击性能和冲击破坏研究方面得到了有效的应用。濮勇等[8]将空气炮冲击试验与高速摄影及数字图像处理技术相结合,研究了夹层玻璃开裂及碎片结构特性。张宗恒等[9]基于落锤试验,研究了不同冲击能量下PVB夹层玻璃的破坏模式。况利民等[10]针对夹层玻璃开展了冲击试验,并分析了冲击速度、夹层厚度、玻璃类型等因素对玻璃试件开裂破坏形态的影响。陈胜等[11]开展了刚球冲击建筑浮法玻璃的破坏试验,并分析了风致飞掷物对建筑浮法玻璃的冲击破坏效应。但是,通常情况下试验结果受限于试验条件及试样尺寸等,且试验成本往往较高,尤其是考虑多种影响因素的情况下。为此,数值模拟方法成为解决该问题的重要研究手段。Xu等[12]基于了扩展有限元法对低速头部碰撞下的汽车挡风玻璃裂纹进行了数值计算,并得到了径向和环向裂纹的扩展特征。陈胜等基于LS-DYNA建立了飞掷物冲击浮法玻璃的有限元模型,并探讨了飞掷物的冲击位置、冲击姿态和外形等特性对其冲击效应的影响。Lin等[13]基于有限元方法研究了汽车挡风玻璃的冲击断裂行为。Chen等[14]采用有限差分法模拟了单颗粒光学玻璃磨削的动态冲击效应。然而,有限元法、扩展有限元法以及有限差分法等传统的数值计算方法,均是基于连续介质假设和空间偏微分方程求解的,在计算多裂缝扩展、分叉等复杂不连续问题时,会遇到计算精度较差和效率低等情况。由Silling[15]提出的基于空间积分方程和非局部作用的近场动力学理论,摆脱了材料不连续处平衡方程失效的限制,在处理断裂问题方面具有独特的优势,故可以有效地模拟裂纹萌生和自由扩展。基于近场动力学方法,Gerstle等[16]有效地模拟了混凝土结构中的损伤和开裂问题;顾鑫等[17]研究了混凝土板侵嵌问题;Hu等[18]探讨了球形弹丸撞击玻璃板的冲击失效破坏机制;Jafaraghaei等[19]分析了玻璃板在冲击载荷下的失效行为。

目前针对冲击荷载作用下玻璃板的结构破坏研究,虽已取得了丰硕的研究成果,但是仍存在一些不足之处。如:上述研究对象主要为夹层玻璃,对于普通建筑玻璃的冲击破坏行为和抗冲击性能研究则涉及较少。同时,目前的研究成果局限于玻璃板宏观裂纹扩展过程及力学行为的定性描述,而对于裂纹网络形态参数的定量化研究则较少。为此,本文基于键型近场动力学方法,建立了低速冲击作用下浮法玻璃板结构损伤及裂纹扩展过程的数值模型,并基于数字图像处理技术将Zhang-Suen细化算法[20]用于裂纹骨架的提取,采用统计分析方法定量计算了裂纹网络的形态参数(裂纹长度、裂纹占比)等,以此来评价刚球初始冲击速度、刚球直径和玻璃板厚度等因素对玻璃损伤和裂纹扩展的影响。

1 键型近场动力学方法

1.1 理论计算模型

经典连续介质力学是一种局部理论,即假设某点仅与其相邻点有相互作用,在采用空间微分方程处理裂纹不连续性问题时会出现奇异性。而近场动力学则基于非局部作用和空间积分方程,将材料视为通过非局部力相互作用物质点或粒子的集合[21],使得该方法能够准确地模拟材料的损伤、裂纹的萌生及扩展过程。近场动力学通过物质点与其近场影响范围内物质点的相互作用来表征宏观的物理力学行为,如图1所示。物质点之间的相互作用由微势能控制,而微势能则与材料本身特性和变形密切相关。物质点间相互作用的影响范围由近场半径δ决定,当δ趋于0时,近场动力学可退化为经典的弹性力学。键型近场动力学是基于成对物质点之间相互作用力大小相等方向相反的假设而建立的,如图2所示。

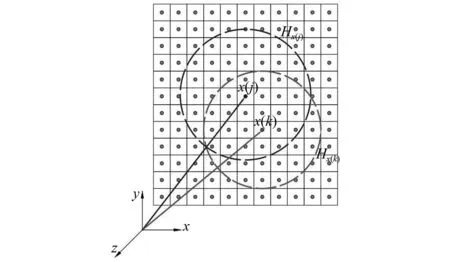
图1 近场动力学物质点x(k)与物质点x(j)之间的相互作用Fig.1 The interaction between particle x(k) and particle x(j) based on peridynamics

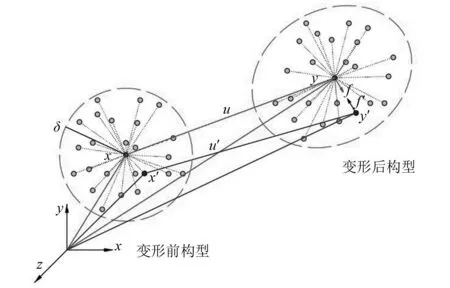
图2 物质点x和x′间的变形及作用力Fig.2 Deformation and forces between particle x and particle x′

物质点在t时刻的运动方程为

(1)

式中:ρ为物质点密度;x为物质点坐标;t为时间;H为近场作用域;u为位移向量;f为力密度矢量;b为外力矢量;x′、u′为近场作用域内物质点的坐标及位移。

力密度矢量f为物质点x′施加在x上单位体积平方的力矢,与物质点间的伸长率呈线性关系,可表示为

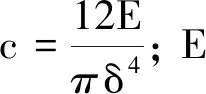
考虑物质点x与其近场作用域内其它物质点x′的相互作用,采用显式向前、向后差分技术对式(1)进行时域积分,可将运动方程离散为

(3)

式中:n为时间步;N为近场作用域内的物质点总数;V为物质点的体积;k、j为物质点号。

根据时间步n的加速度和速度,可计算出时间步n+1的速度;同理,由时间步n的位移和时间步n+1的速度,可确定时间步n+1的位移。相应的计算公式为

(4)

(5)

式中:k为第k个物质点;Δt为时间步步长。

当邻域物质点位于近场边界附近时,会出现近场作用域不完整的情况,即,部分体积在近场作用域以外,故须引入体积修正因子vc(j)

(6)

式中:r=Δ/2为到近场作用域表面的距离;Δ为物质点间距;ξ(k)(j)=|x(j)-x(k)|为物质点之间的距离。

引入体积修正因子后,运动离散方程式(3)可改写为

(7)

1.2 结构损伤定义

在近场动力学方法中,材料损伤是通过物质点之间相互作用键的断裂来表征的。当两个物质点之间的伸长率s超过临界伸长率sc时,就会产生键的断裂,这就意味着两点之间的作用力发生不可逆地消除。考虑键断裂的影响,将材料的损伤定义为

(8)

式中:φ为损伤变量,取值范围为[0,1],当φ=0为该物质点与其近场作用域内所有物质点间的作用键完好,而φ=1则表示作用键全部断裂;μ为标量函数,表示物质点对的键破坏情况,表达式为

(9)

键临界伸长率sc的取值与临界能量释放率Gc有关,可表示为[22]

(10)

式中,E为材料的弹性模量。

1.3 刚体冲击作用机制

将冲击物视为刚性球体,以初始速度v0与被冲击物发生撞击;而被冲击物的变形则由近场动力学运动方程控制,整个冲击过程如图3所示。当两个物体发生接触时,存在相互贯穿的现象,而实际情况中并不存在这样的接触,故须将穿透到冲击物内部的物质点重新定位至冲击物外的新位置处,这些物质点的新位置为距离冲击物表面最近点的坐标。刚性球体的冲击过程主要通过以下5个步骤实现:

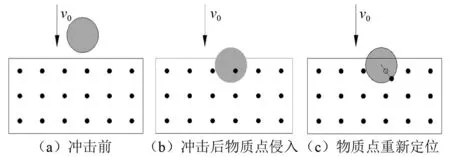
图3 冲击过程示意图Fig.3 Schematic diagram of impact process

步骤1搜寻侵入刚球内部的物质点。遍历被冲击物上的所有物质点,并计算其到球心的距离dm,如dm小于刚球半径r,则该物质点侵入刚球内部,需重新定位。

步骤2确定侵入刚球内部物质点的新坐标。首先计算球心与侵入刚球内部物质点连线的外法线方向;然后将该物质点沿法线方向移至刚球表面,如图3(c)所示。

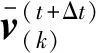
(11)

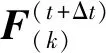
(12)

将侵入刚球内部所有物质点对刚球的冲击反力进行求和,可得t+Δt时刻冲击物受到的反作用力F(t+Δt)

(13)

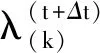
(14)

步骤5根据牛顿第二定律更新下一时间步刚球的加速度、速度及位移。

1.4 裂纹骨架提取及形态参数量化

为了对玻璃板的冲击破坏效果进行定量的评价,根据近场动力学的数值计算结果,将φ>0.4的物质点定义为裂纹,标记为1;其它物质点标记为0,由此得到二值化的裂纹网络结构图。同时,基于数字图像处理技术将Zhang-Suen细化算法应用于裂纹网络骨架的提取,用于表征裂纹形态及扩展规律[23],图4为裂纹损伤结构图与提取骨架图的对比。最后,采用统计方法对裂纹网络进行量化计算,并提出了以下形态参数:

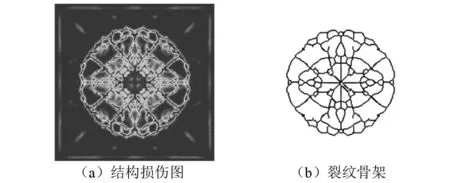
图4 裂纹损伤结构图与提取骨架对比Fig.4 Comparison between crack damage structure and extracted skeleton

(1)裂纹占比De:裂纹物质点面积与计算域总物质点面积之比

(15)

式中:Sd为损伤值大于0.40的物质点面积;St为计算域总物质点面积。

(2)裂纹长度:将裂纹骨架物质点的长度相加,即为裂纹长度

(16)

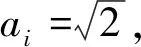
2 算例验证

Kalthoff-Winkler试验[24-25]是经典的金属动态断裂问题。试验中将冲击物视为圆柱状刚体,其直径为D0=0.05 m,高度为H=0.05 m,初始冲击速度为v0=-32 m/s。受冲击钢板长为L=0.2 m,宽为W=0.1 m,厚度h=0.009 m,弹性模量为E=191 GPa,泊松比为υ=0.25,密度为ρ=8 000 kg/m3。钢板中对称分布两条裂缝,其宽度为a0=0.001 5 m,长度为h0=0.05 m,裂缝间距为d=0.05 m。钢板不受位移约束,且初始处于静止状态,在圆柱体的冲击下发生动态断裂破坏。计算模型如图5所示。

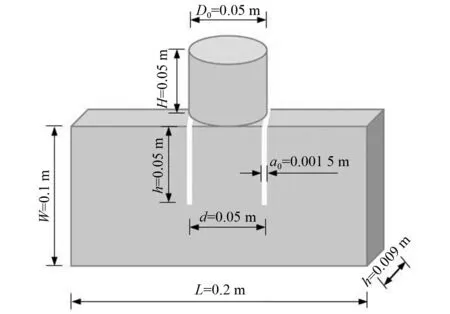
图5 Kalthoff-Winkler试验模型Fig.5 Kalthoff-Winkler experiment model

基于键型近场动力学方法,针对圆柱状刚体冲击带裂缝钢板,致使其发生断裂破坏过程进行了数值计算,图6为计算得到的结构损伤图。该数值模型计算得到的钢板裂纹扩展方向与中轴线的夹角为67.49°,这与文献[24]的试验结果夹角为68°非常吻合。同时,钢板裂纹的起裂时间约为28.7 μs,与试验得到的起裂时间略低于29 μs也较为一致。这充分证明了本文计算模型在处理刚体冲击导致结构产生裂纹及裂纹扩展方面,具有较好的适应性和计算精度。

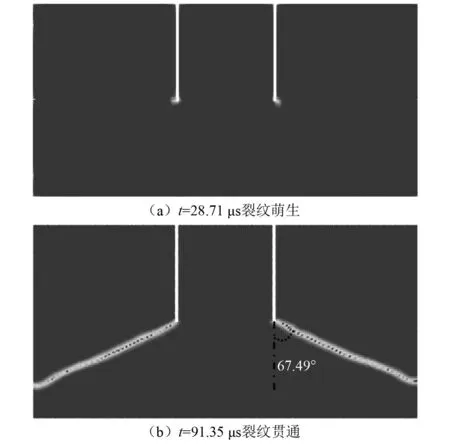
图6 Kalthoff-Winkler试验数值计算结果Fig.6 Simulated damage cloud image of Kalthoff-Winkler experiment

3 计算结果讨论

为了研究刚体冲击作用下玻璃板的裂纹破坏形态,基于键型近场动力学方法,通过编写Fortran代码建立了刚球低速冲击浮法玻璃板的三维数值模型,如图7所示。玻璃板长为L=100 mm,宽为W=100 mm,厚度为h=3 mm,板的四周受固定约束。刚球与玻璃板的净距为t=2 mm,刚球直径为D=10 mm,初始速度为v0=10 m/s。玻璃板的材料参数为:密度为ρ=2 530 kg/m3,弹性模量为E=72 GPa,泊松比为υ=0.25。近场动力学模型参数为:物质点间距Δ=0.5 mm,近场邻域半径为δ=3.015Δ=1.508 mm,键的临界伸长率为sc=0.000 1,时间步长为Δt=8.7×10-8s。为了探究刚球初始冲击速度、刚球直径和玻璃板厚度等因素,对刚球冲击玻璃板破坏形态的影响,设计如表1所示的计算工况。

表1 计算工况Tab.1 Design of calculation conditions

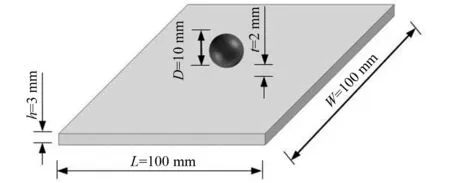
图7 刚球冲击玻璃计算模型Fig.7 Calculation model for rigid ball impact glass

3.1 初始冲击速度

为了研究刚球初始冲击速度对玻璃板破坏形态的影响,针对冲击速度v0分别为5 m/s、10 m/s、15 m/s、20 m/s、25 m/s的工况一分别进行了数值计算,得到的玻璃板结构损伤特征及裂纹网络骨架分别如图8、图9所示。由图可知:采用Zhang-Suen细化算法所提取的裂纹网络骨架能够反映出玻璃板破坏形态的变化。随着刚球初始冲击速度的增大,玻璃板的碎裂化程度加剧。当冲击速度大小为5 m/s时,裂纹沿着最大应力方向呈辐射状扩展,环状裂纹则较为不明显;随着冲击速度的增加,冲击点附近的局部破坏面积逐渐扩大,结构损伤加剧,而裂纹分支数量也趋于增多,且径向裂纹的尖端向边界扩展。径向裂纹尖端倾向于同相邻的裂纹尖端连接形成环状裂纹,并构成由环向裂纹和径向裂纹组成的裂纹网络。当冲击速度增加至15m/s时,玻璃板出现了大规模破坏,裂纹数量增多,并伴随裂纹分支的扩展和贯通。此后,随着冲击速度的进一步增加,玻璃板裂纹网络形态变化较小,但损伤程度进一步加剧。本文的玻璃板冲击破坏的裂纹网络形态与文献[26]的试验结果表现出了较好的一致性。

图8 不同冲击速度下玻璃板的结构损伤图Fig.8 Structure damage images of glass panels under different impact velocities

图9 不同冲击速度下玻璃板的裂纹网络骨架Fig.9 Crack network skeleton of glass panels under different impact velocities

图10为不同初始冲击速度作用下玻璃板中裂纹占比及裂纹长度的演化趋势。由图可知,裂纹长度和裂纹占比均随初始冲击速度的增加而增大,且近似呈线性规律。当冲击速度v0≤15 m/s时,随着冲击速度的增加裂纹长度增加显著;此后裂纹长度增加趋势略有减缓,这表明此时玻璃板的碎裂化程度已较为严重,裂纹扩展已趋于边界。而裂纹占比的变化趋势则未表现出较大的波动现象,说明随着冲击速度的增加裂纹宽度也逐渐增大,在一定程度上弥补了裂纹长度增加趋势减缓的损失。

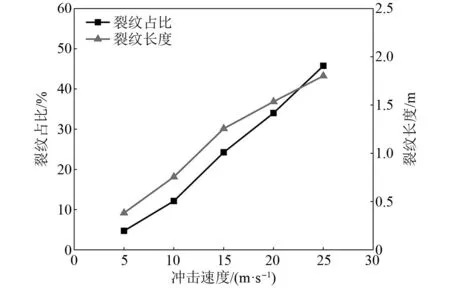
图10 裂纹形态参数与冲击速度间的关系Fig.10 Relationship between crack morphology parameters and impact velocity

图11为不同初始冲击速度下刚球的速度时程曲线。由图可知,刚球与玻璃板接触后在极短的时间内速度迅速降低,之后速度平稳下降直至穿透玻璃板。同时,初始冲击速度越大,刚球与玻璃板的冲击作用持续时间越短,刚球速度减小值也越大,刚球对玻璃板的冲击力也越大,从而造成玻璃板的裂纹网络更加复杂,结构碎裂程度加剧。

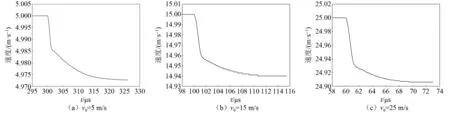
图11 不同初始冲击速度情况下刚球的速度时程曲线Fig.11 Velocity time history curves of rigid ball under different initial impact velocities

3.2 刚球直径

刚球直径直接影响着冲击过程中玻璃板结构的损伤以及裂纹网络形态的发展。为了研究刚球直径对玻璃板冲击破坏的影响,针对工况二刚球直径分别为D=2 mm、4 mm、6 mm、10 mm、14 mm五种情况下的玻璃板冲击破坏过程进行了数值计算,其结构损伤情况如图12所示。由图12可知:随着刚球直径的增加,其与玻璃板的接触区范围扩大,致使玻璃板的损伤程度加剧,且更易形成结构复杂的裂纹网络。当刚球直径D=2 mm时,玻璃板裂纹呈十字放射状分布,且裂纹分支并不明显。随着刚球直径的增加,其结构破坏范围逐渐扩大,裂纹分支也愈发显著,且环状裂纹增多,各裂纹之间逐渐连通、交叉,并形成了复杂的裂纹网络。

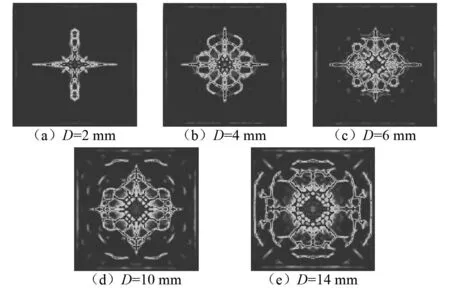
图12 不同刚球直径下玻璃板的结构损伤图Fig.12 Structure damage images of glass panels under different rigid ball diameters

图13为裂纹形态参数(裂纹占比和裂纹长度)与刚球直径间的关系。由图13可知:裂纹占比和裂纹长度呈现出相似的变化趋势,且均随着刚球直径的增加而显著增大。当刚球直径D从2 mm增加至4 mm的过程中,裂纹形态由十字放射状转化为放射环状发生了显著变化,故裂纹占比和裂纹长度均发展迅速;当刚球直径D增加至6 mm时,玻璃板结构损伤变化不大,故裂纹形态参数变化有减缓的趋势。此后,随着刚球直径的进一步增大,玻璃板碎裂化程度加剧,裂纹形态参数也显著增加,且均与刚球直径近似呈线性关系。图14为不同直径刚球的速度演化时程曲线,由图14可知:随着刚球直径的增加,在与玻璃板撞击后其速度损失逐渐增大,且速度衰减趋势随直径增加而加剧。当刚球直径分别为2 mm、4 mm、6 mm、10 mm及14 mm时,其速度衰减量分别为:0.013 2 m/s、0.019 4 m/s、0.025 6 m/s、0.043 1 m/s以及0.068 5 m/s。因此刚球直径增加使得其对玻璃板的冲击力也相应的增大,这也是导致玻璃板结构损伤以及裂纹形态参数变化加剧的重要因素。

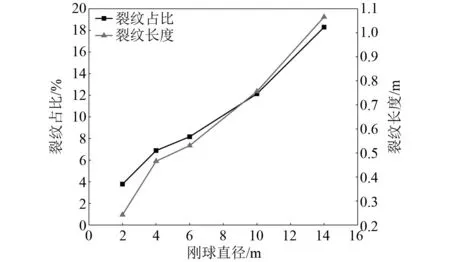
图13 裂纹形态参数与刚球直径间的关系Fig.13 Relationship between crack morphology parameters and rigid ball diameter

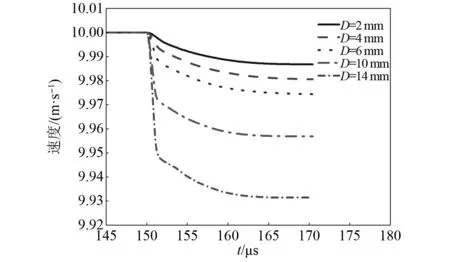
图14 不同直径情况下刚球的速度时程曲线Fig.14 Velocity time history curves of rigid ball with different diameters

3.3 玻璃板厚度

为了研究同等刚球冲击条件下,玻璃板厚度对其结构损伤及冲击破坏的影响,针对工况三厚度为h=1.5 mm、3.0 mm、4.5 mm、6.0 mm及7.5 mm五种情况时的玻璃板冲击破坏过程进行了数值计算,并得到了相应的结构损伤结果,如图15所示。从图中可以明显看出:玻璃板厚度越大,其结构损伤范围越大且碎裂化程度越显著,而裂纹扩展分支也增加越多,裂纹形态逐渐趋于复杂化。当玻璃板厚度较小(h=1.5 mm)时,其冲击过程迅速完成,在刚球与玻璃板接触部位附近的局部结构损伤较为严重,但整体影响范围较小;随着玻璃板厚度的增加,其结构损伤的影响范围显著扩大,而冲击点附近的局部结构损伤则有所减弱。

图15 不同玻璃板厚度下结构损伤图Fig.15 Structure damage images of glass panels with different thickness

图16为玻璃板破坏时的裂纹形态参数(裂纹占比与裂纹长度)与其厚度间的关系。由图16可知:裂纹占比与裂纹长度均随玻璃板厚度的增加而增大,且变化趋势略有减缓。产生这种现象的原因主要是由于玻璃板厚度越大,刚球冲击持续时间越长,速度衰减量也相应的增加,如图17所示,从而导致玻璃板所承受的冲击能有所增加。当玻璃板厚度从h=1.5 mm增加至7.5 mm过程中,速度衰减量从0.014 4 m/s增加至0.270 8 m/s,增加显著;而冲击持续时间则由14.268 μs增加至47.154 μs,故刚球对玻璃板各部分的扰动并非同时发生,而是存在一个历时过程,这也是导致玻璃板裂纹结构复杂化、影响范围扩大、碎裂化程度加剧的重要原因。

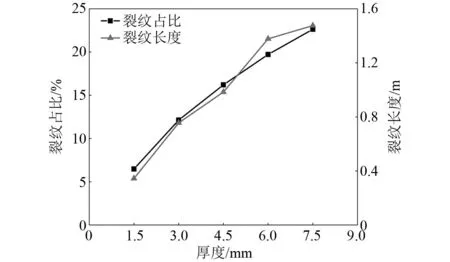
图16 裂纹形态参数与玻璃板厚度间的关系Fig.16 Relationship between crack morphology parameters and glass panel thickness

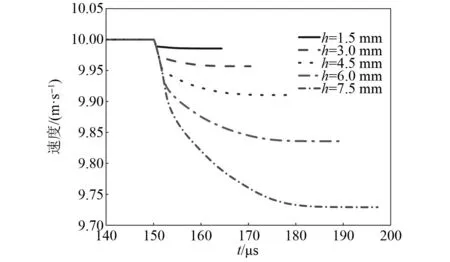
图17 不同板厚情况下刚球的速度时程曲线Fig.17 Velocity time history curves of rigid ball under different glass panel thicknesses

4 结 论

基于键型近场动力学方法,考虑冲击作用下结构损伤产生断裂破坏影响,建立了刚性球体冲击玻璃板的三维数值计算模型。同时,采用数字图像处理技术对玻璃板的裂纹破坏形态进行了量化统计分析。最后,探究了刚球冲击作用下初始冲击速度、刚球直径以及玻璃板厚度等因素,对玻璃板冲击破坏结构形态、裂纹扩展机制的影响,得出以下结论:

(1)基于键型近场动力学方法,针对Kalthoff- Winkler试验过程进行了数值计算,从裂纹扩展方向以及起裂时间来看,本文数值计算结果与试验结果非常吻合,验证了本文计算模型在处理刚体冲击致结构破坏问题的可靠性。

(2)刚球的初始冲击速度对玻璃板的裂纹扩展形态有着显著影响。当初始冲击速度较小时,裂纹以径向辐射状为主,随着冲击速度的增加,径向裂纹尖端间倾向于形成环状裂纹,并形成放射环状的复杂裂纹网络。故刚球初始冲击速度越大,其对玻璃板的冲击力也越大,从而造成玻璃板结构的碎裂程度加剧。此外,玻璃板的裂纹长度和裂纹占比均随初始冲击速度的增加而增大,且近似呈线性关系。

(3)当刚球直径较小时,玻璃板裂纹呈十字放射状径向扩展。随着刚球直径的增加,玻璃板的损伤程度会加剧,且裂纹网络倾向于复杂化。同时,刚球与玻璃板撞击后其速度损失量随直径的增加而逐渐增大,且速度衰减趋势也加剧,使得其对玻璃板的冲击力增加,从而加重结构的损伤破坏。

(4)随着玻璃板厚度的增加,刚球冲击持续时间越长,速度衰减量也相应地增加,从而导致玻璃板所承受的冲击能有所增加,因此当玻璃板厚度较小时,刚球与玻璃板接触部位附近结构损伤严重,但整体影响范围较小;而当厚度较大时,其结构损伤的影响范围扩大,而冲击点附近的局部损伤则有所减弱。