基于磁性阻尼动力吸振器的管道减振技术研究

周 帅, 高红波, 林 磊, 陈志林, 徐德城, 陈明亚

(苏州热工研究院有限公司,江苏 苏州 215004)

管道振动是核电和火电等电力行业长期存在的问题[1-5]。引起管道振动的原因众多,通常可归纳为流致管道振动、机械强迫管道振动、管道共振等。管道振动的主要危害为引起自身的金属疲劳破坏、导致附属小支管的疲劳破坏以及造成与之相连的支吊架的松动或损坏。电力行业的管道振动治理是目前的热门研究问题,林磊等[6]针对核电厂仪表管道振动疲劳耐久性能的改进开展研究,发现通过增大管道外径和壁厚、改变焊接形式等措施能够显著改进结构低频共振。陈锐等[7]对600 MW机组高压加热器至除氧器疏水管道的振动开展治理工作,通过调高管道刚度和加装阻尼器等措施实现了疏水管道的振动治理。薛宪阔等[8]对1 000 MW核电机组再循环管道开展振动分析和治理,通过支架改造和流体系统改造,有效消除了管系的振动。王树升等[9]对核电厂碱计量泵出口管道振动开展分析及治理工作,通过更换管道原有弹性支撑和在合理位置增加支撑后,改变了管道固有频率,最终降低了管道系统的振动。综上所述,电力行业管道振动治理的方案主要为改造流体系统消除振源和改变管道本身刚度避免共振。但是,有时管道内部流动异常复杂,不易消除振源。有时现场管道所在位置空间狭窄,无法在合适的位置增加支架。而动力吸振器作为一种无根减振器可以实现在狭窄空间管道上进行安装。动力吸振器在轨道车辆等领域已有大量应用研究。孙倩等[10]对城市轨道车辆车体复合吸振器进行了建模与仿真研究,结果表明安装复合吸振器后,对车体刚性和弹性振动都有较好的减振效果。白世鹏等[11]开展了动力吸振器对车辆垂向振动能量及悬架性能的影响研究,发现对于简谐路面激励和随机路面激励,簧上吸振器侧重于提升车辆的悬架性能,簧下吸振器可以吸收更多的振动耗散能量。刘国政等[12]对动力吸振器在驱动桥减振降噪上的应用开展仿真和试验研究,结果表明,安装动力吸振器后的桥壳振动幅值降低75%左右。徐涆文等[13]针对钢轨动力吸振器对轮轨振动噪声的影响开展分析研究,发现在轨腰位置安装钢轨动力吸振器对轮轨振动噪声降低效果较好,降噪量为3.2dBA。另外,大量国外学者也对动力吸振器对结构的振动治理效果开展了大量研究工作[14-16]。动力吸振器在管道减振方面也有应用,陈果等[17]研发了一种用于管道减振的新型动力吸振器(悬臂式结构),主要由夹持件、弹簧片和质量块组成,并设计了实验室三维管路进行减振验证,结果表明可将共振频率下的振动降低90%以上。刘彬彬等[18-19]在陈果开发的新型动力吸振器基础上进行改进,发明了可调谐的新型动力吸振器。黄秀金等[20]研究了一种可控环形动力吸振器在抑制管道强迫振动中的应用,使用了四根弹簧可以抑制较宽的频带的振动。张炳康等[21]开展了悬臂式调谐质量阻尼器抑制管道振动研究,结果表明所设计的动力吸振器可以抑制300 Hz左右的高频振动。综上所述,管道振动问题研究和动力吸振器在各种结构的减振研究一直是热点问题,动力吸振器在管道减振中的应用也已开展一定的研究工作。但仍存在一些不足,如用于管道减振的悬臂式动力吸振器,吸振器本身的弹簧片承受较大的弯曲应力,可能存在频率断裂问题;可控环形动力吸振器的质量块基本由弹簧支撑,可能存在结构不稳定的问题。另外,动力吸振器的安装位置的最优化研究目前尚未开展。因此,本文将设计一种新型的基于磁性阻尼的动力吸振器,并对其安装位置的最优化和减振效果进行研究。

1 动力吸振器设计

1.1 基本原理

主振系统上附加动力吸振器的力学模型如图1所示。f=Fsinωt,为激励力;x1、x2分别为主振系统和动力吸振器的位移;K为主振系统的刚度;k为动力吸振器的刚度;m为动力吸振器质量块的质量;c为动力吸振器的阻尼系数。

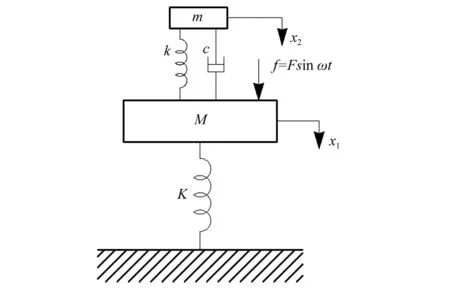
图1 力学模型Fig.1 Mechanical model

系统的运动方程如式(1)

(1)

将激励力和位移分别通过复数形式表示。求解方程,可得式(2)和式(3)

(2)

(3)

分子分母同除以(Mω)2,并引入以下各项

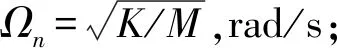
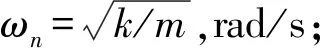
Xst为主振系统的静变形,Xst=F/K,m;

μ为质量比,μ=m/M;

ζ为阻尼比,ζ=c/(2mΩn);

λ为强迫振动频率比,λ=ω/Ωn;

γ为固有角频率比,γ=ωn/Ωn;

(4)

(5)

(6)

(7)

X1/Xst称为位移的振幅比,动力吸振器的设计目标即为使该值最小。根据定点理论[22],当满足最优同调和最优阻尼条件时,可实现位移振幅比最小的设计目标。

1.2 最优设计公式

满足最优同调条件时,可得动力吸振器和主振系统的固有频率比为

(8)

满足最优阻尼条件时,得到最优阻尼表达式

(9)

满足最优设计条件下的振动系统的最大振幅比

(10)

根据上述最优同调和最优阻尼条件,可以推导出质量比μ构成的动力吸振器的3个元素的设计公式。

动力吸振器的质量

m=μM(kg)

(11)

动力吸振器的弹簧刚度

(12)

动力吸振器的阻尼系数

(13)

基于Visual Basic编程软件,将动力吸振器的关键参数求解程序化,并设计人机交互界面,方便参数计算和调整,如图2所示。

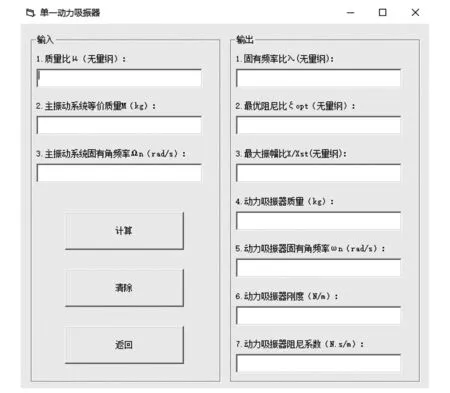
图2 动力吸振器关键参数计算器Fig.2 Key parameter calculator

1.3 设计流程

一般应用于三维管道减振的单向有阻尼动力吸振器设计流程如下:

(1)确定对三维管路的前n阶模态开展振动治理;

(2)有限元仿真软件计算三维管路动力学特性参数:模态质量、固有频率、模态刚度、模态振型;

(3)动力吸振器的关键参数计算:质量、刚度、阻尼系数;

(4)动力吸振器的结构设计:结构形式、各部件形状尺寸、安装尺寸;

(5)有限元仿真计算初步验证振动治理效果;

(6)试验验证振动治理效果。

1.4 安装位置优化

在动力吸振器安装位置优化中,以安装位置参数为优化变量,以管道结构在前3阶固有频率下的振动响应为优化目标函数。安装位置优化涉及多个目标函数,因此采用精英策略的非支配排序遗传算法(the non-dominated sorting genetic algorithm-Ⅱ,NSGA-Ⅱ)[23]。相对把多个目标函数整合成单目标的经典多目标优化算法,该方法基于Pareto对目标演化机制,同时在进行选择操作之前对个体进行了快速非支配排序、采用了精英策略并引入拥挤度策略代替了需指定共享半径的适应度共享策略,从而提升了运算效率和计算精度。算法实现流程如图3所示。

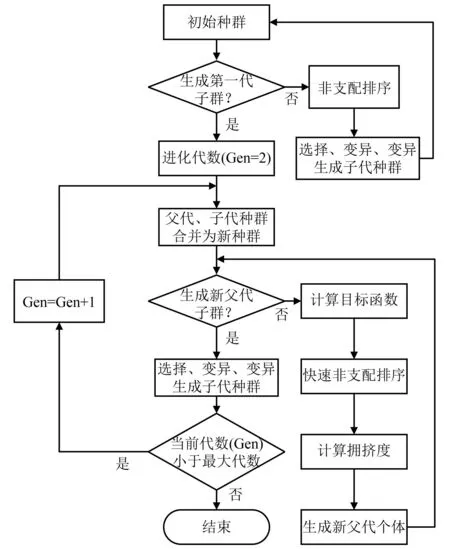
图3 算法实现流程Fig.3 Algorithm implementation flow

2 管道减振案例

2.1 三维管路

图4为试验用三维管路,作为振动治理对象,管路参数如表1所示。三维管路由5段管跨组成,管跨①～管跨⑤的长度依次为1 000 mm、1 000 mm、1 500 mm、1 000 mm和500 mm。其中,管跨①下端通过夹具和螺栓固定在振动台上,由振动台在该处进行激振。

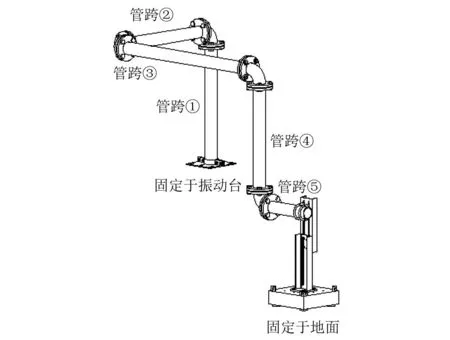
图4 三维管路示意图Fig.4 Three-dimensional pipeline diagram

表1 管路参数

通过有限元仿真对三维管路开展模态分析,模型如图5所示,将其两端固定约束,采用solid185单元,共8 358个单元,43 854个节点。

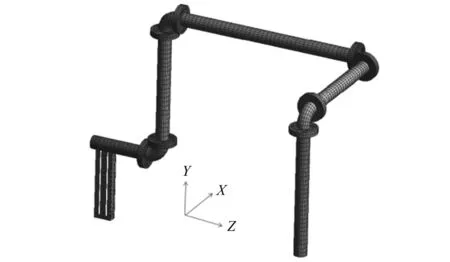
图5 有限元模型Fig.5 Three-dimensional pipeline design drawing

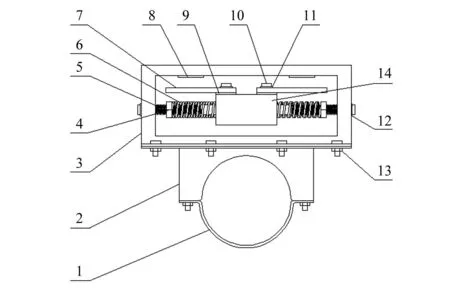
1-下卡箍; 2-上卡箍; 3-壳体; 4-紧固螺母; 5-质量块滑杆; 6-弹簧; 7-导体板; 8-永久磁铁; 9-绝缘垫; 10-螺栓; 11-螺栓绝缘垫; 12-螺栓垫圈; 13-螺母; 14-质量块

采用分块法对三维管路前3阶模态进行提取,获得如表2所示的模态参数。针对前3阶模态设计的动力吸振器分别命名为TMD1、TMD2、TMD3。

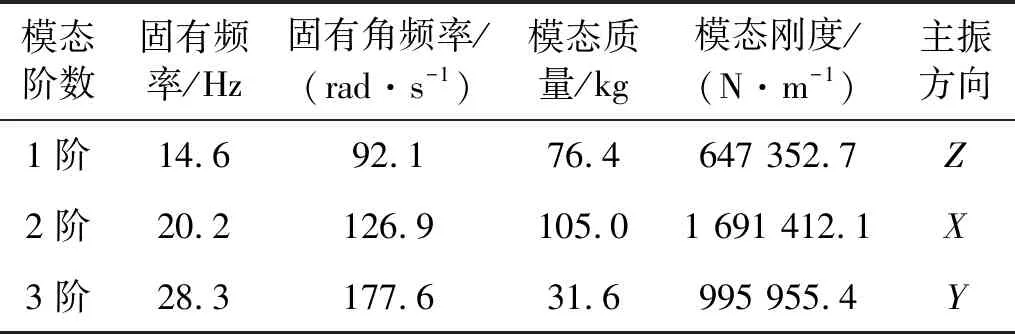
表2 模态参数

2.2 动力吸振器参数计算

将模态分析获取的三维管路前3阶模态参数输入单一动力吸振器的参数计算器中,得到结果如表3所示。

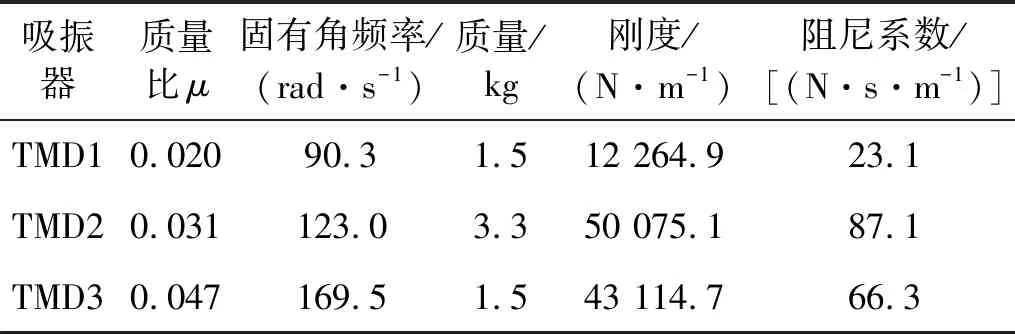
表3 单一动力吸振器优化设计计算结果

2.3 动力吸振器结构设计

设计适用于管道结构的单一动力吸振器如图5所示,主要由质量块、弹簧、永久磁铁和导体板、上下卡箍等结构组成。其中质量块提供质量、弹簧元件提供刚度、永久磁体和导体板提供磁性阻尼、上下卡箍用于管道固定。质量块和弹簧材质均为不锈钢,导体板材质为铜,永久磁体材料为磁铁,其余材料为铝。

上下卡箍的尺寸根据管道直径确定,质量块的尺寸按照其质量进行设计,弹簧尺寸和电磁阻尼元件尺寸参数的确定按下面方法。

(1)弹簧设计

根据标准GB/T 2089—2009[24]对弹簧进行选型,确定弹簧材质、卷线直径、卷簧有效直径等基本参数,通过控制弹簧长度来确定弹簧刚度。适用于三维管路前3阶模态的弹簧参数如表4所示,其中单个动力吸振器中使用4根弹簧,单根弹簧的刚度为动力吸振器所需弹簧刚度的1/4。

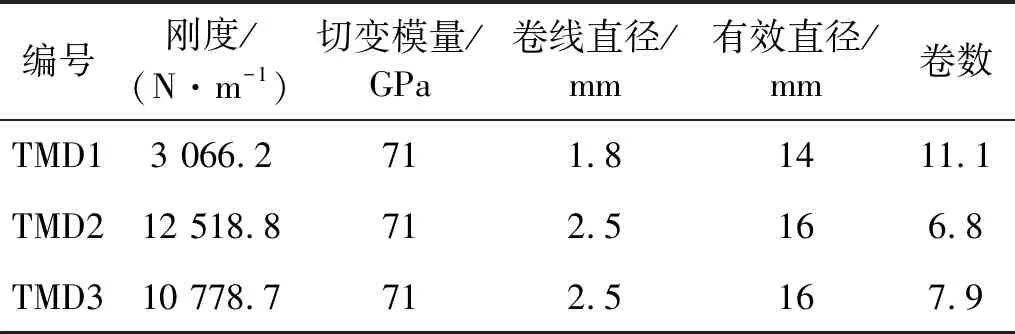
表4 弹簧参数

(2) 磁性阻尼结构设计

磁性阻尼结构的基本构成如图7所示,主要由永磁体和导体组成。

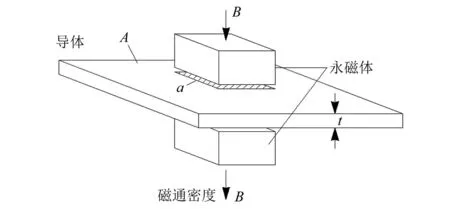
图7 磁性阻尼结构示意图Fig.7 Schematic diagram of magnetic damping structure

根据动力吸振器的结构尺寸,首先确定导体板尺寸、导体板材质(确定导体电阻)、永久磁体磁极面积等参数,参考《动力吸振器及应用》确定所需的平均磁通密度,通过选用不同磁性的永磁体和调节导体与永磁体的相对位置来调节磁通密度。磁性阻尼结构的设计参数如表5所示,单个动力吸振器有两个磁性阻尼结构,单个磁性阻尼结构的阻尼系数为动力吸振器阻尼系数的1/2。

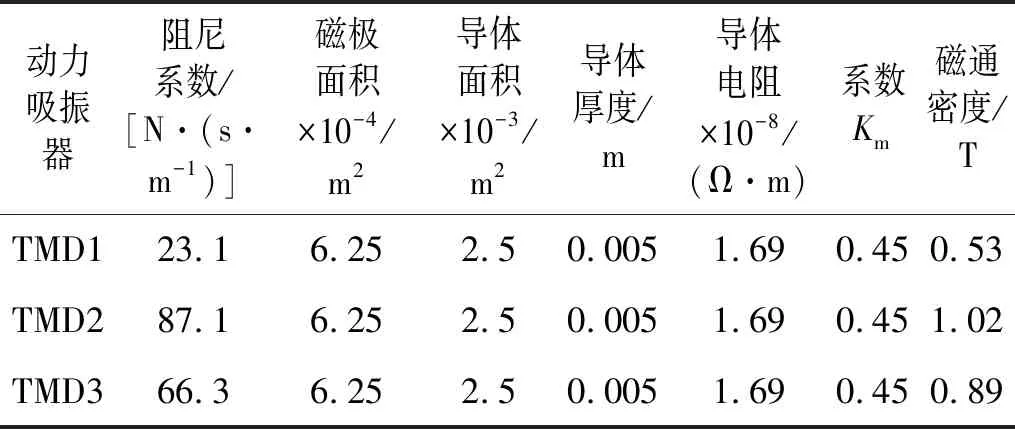
表5 磁性阻尼结构参数

动力吸振器的最终设计结构如图8所示,安装示意如图9所示,本文设计的动力吸振器的质量块、弹簧、永久磁铁和导体板等均集中布置在吸振器壳体内,具有结构紧凑的特点。质量块本体开孔,穿过两根滑杆(接触设置有无油衬套,减小摩擦,提高耐磨性),提高了质量块振动的稳定性。该动力吸振器的质量块在弹簧之间振动,弹簧为主要弹性受力元件,其受力特性强于弹性片结构。

图8 单一动力吸振器三维结构图Fig.8 3D structure diagram

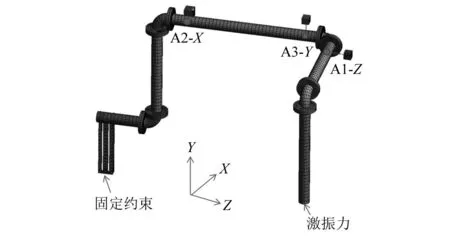
图9 单一动力吸振器安装图Fig.9 Installation diagram

2.4 仿真验证

为初步验证质量块质量、弹簧刚度和阻尼系数选择的正确性,开展仿真验证。分别建立安装动力吸振器前后的有限元模型,如图10所示。将动力吸振器简化为带阻尼的弹簧振子结构,弹簧刚度、阻尼系数和振子质量均为2.3节中计算所得,三维管路系统的阻尼比设置为0.02。三维管路槽钢支架端采用固定约束,激励端在X方向施加2 m/s-2的激振加速度,该激振加速度通过远大于管道系统质量的质量点施加。通过谐响应分析模块,计算10～35 Hz内的管道振动加速度响应,加速度提取点和提取方向如图10中所示的A2-X(2阶模态振动最大点的X方向)、A3-Y(3阶模态振动最大点的Y方向)和A1-Z(1阶模态振动最大点的Z方向),结果如图11所示。

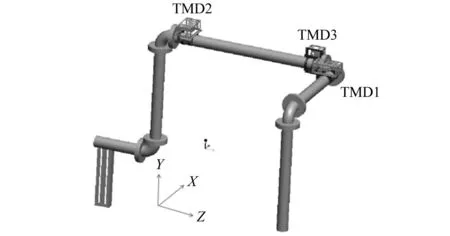
图10 有限元模型Fig.10 Finite element model

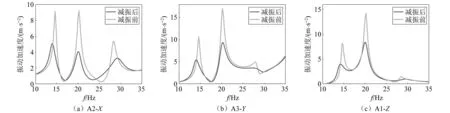
图11 加速度/频率曲线(仿真)Fig.11 Acceleration/frequency curve (simulation)

安装减振器后三维管路各振动加速度提取点在10～35 Hz之间的振动加速度峰值均减小,该频率范围减振效果如表6所示,各提取点的减振效果在27.1%～55.8%之间。

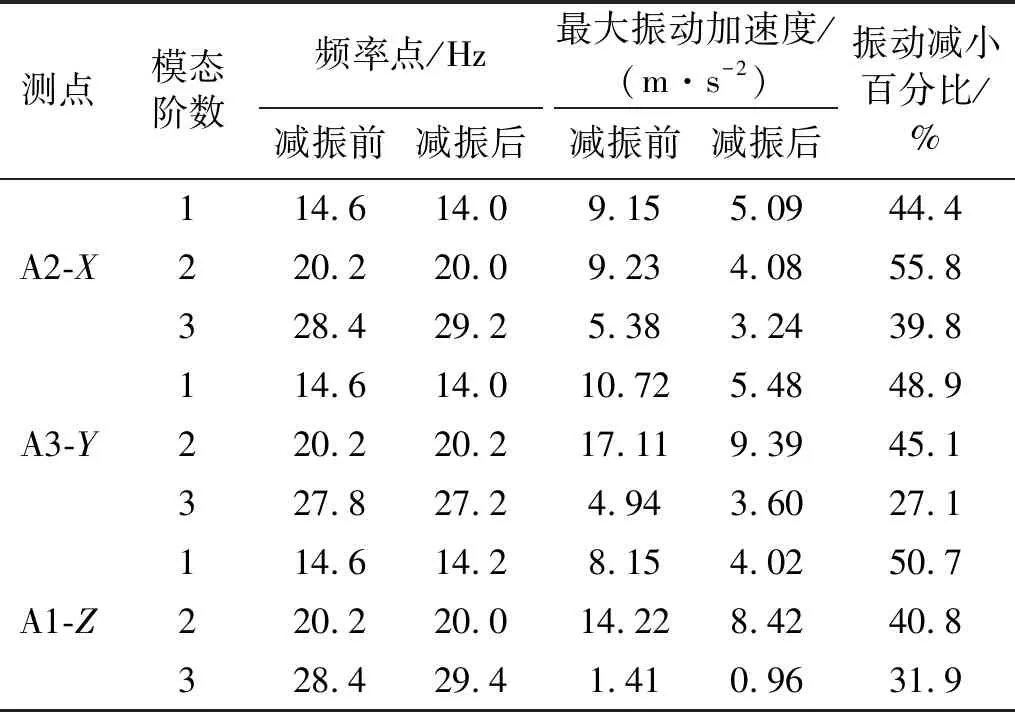
表6 减振前后最大振动加速度对比(仿真)

2.5 安装位置优化

如图12所示,以安装位置参数为优化变量,以管道结构在前3阶固有频率下的振动响应为优化目标函数,采用NSGA-Ⅱ算法开展优化计算。

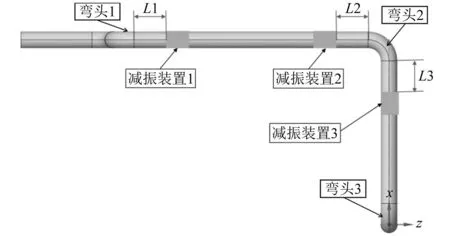
图12 减振装置安装位置Fig.12 Installation position of vibration damping device

安装位置优化计算结果如表7所示,优化方案安装位置参数L1、L2、L3分别为0.411 m、0.010 m、0.071 m,相对于初始计算方案(人工选择的最优安装位置),管道振动位移响应在第1阶、第2阶固有频率下的振动位移响应均呈现不同程度下降,第3阶固有频率下的振动位移响应有所上升。但相对于未加装动力吸振器的情况,优化方案的管道振动位移响应均下降了50%以上,说明通过NSGA-Ⅱ算法开展动力吸振器安装位置优化计算具有一定可靠性。

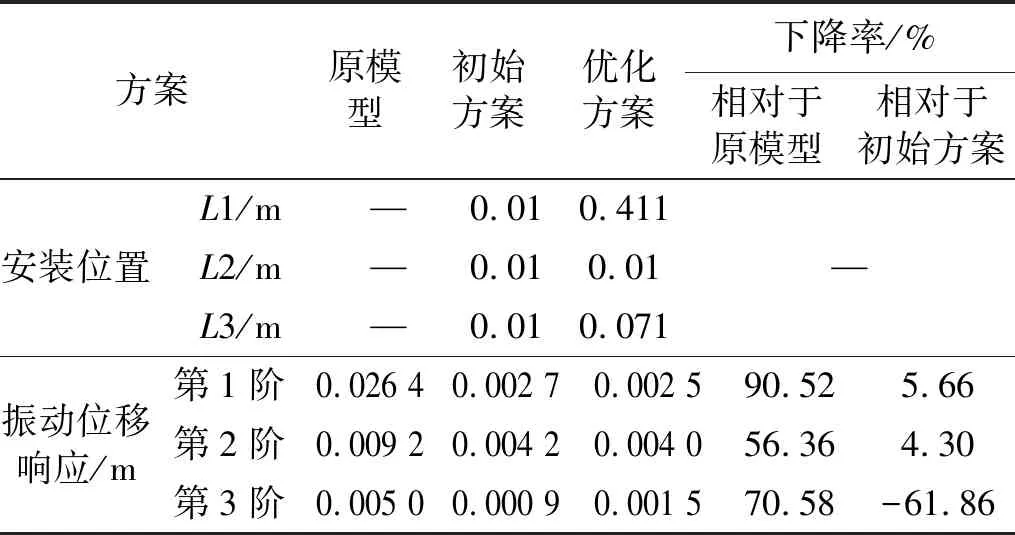
表7 安装位置优化结果

2.6 试验验证

图13为搭建的试验管路并安装动力吸振器,关键试验参数为:水平振动台的激振加速度设置为2 m/s2,扫频范围为10～35 Hz,扫频速率为0.2 Hz/s。在图10所示仿真计算加速度提取点位置安装振动加速度传感器。

图13 试验管路Fig.13 Test pipeline

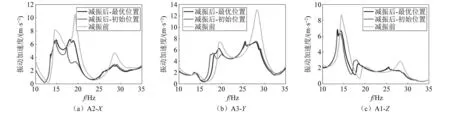
图14 加速度/频率曲线(试验)Fig.14 Acceleration/frequency curve (test)

开展3次管路振动试验,分别为:试验(1)光管振动试验(未安装动力吸振器);试验(2)含动力吸振器管路试验(初始安装位置,L1=0.020 m、L2=0.020 m、L3=0.020 m),试验(3)含动力吸振器管路试验(最优安装位置,L1=0.411 m、L2=0.01 m、L3=0.071 m)3次试验中振动加速度随激振频率变化曲线如图13所示。

安装动力吸振器后(初始安装位置和最优安装位置)三维管路各振动加速度测点在10～35 Hz之间的振动加速度峰值普遍减小,优化结果如表8所示。其中,TMD1吸振器将主作用Z方向的振动减小23.0%,TMD2吸振器将主作用X方向的振动减小35.5%,TMD3吸振器将主作用Y方向的振动减小43.2%,减振效果明显,且减振效果与仿真计算相近。

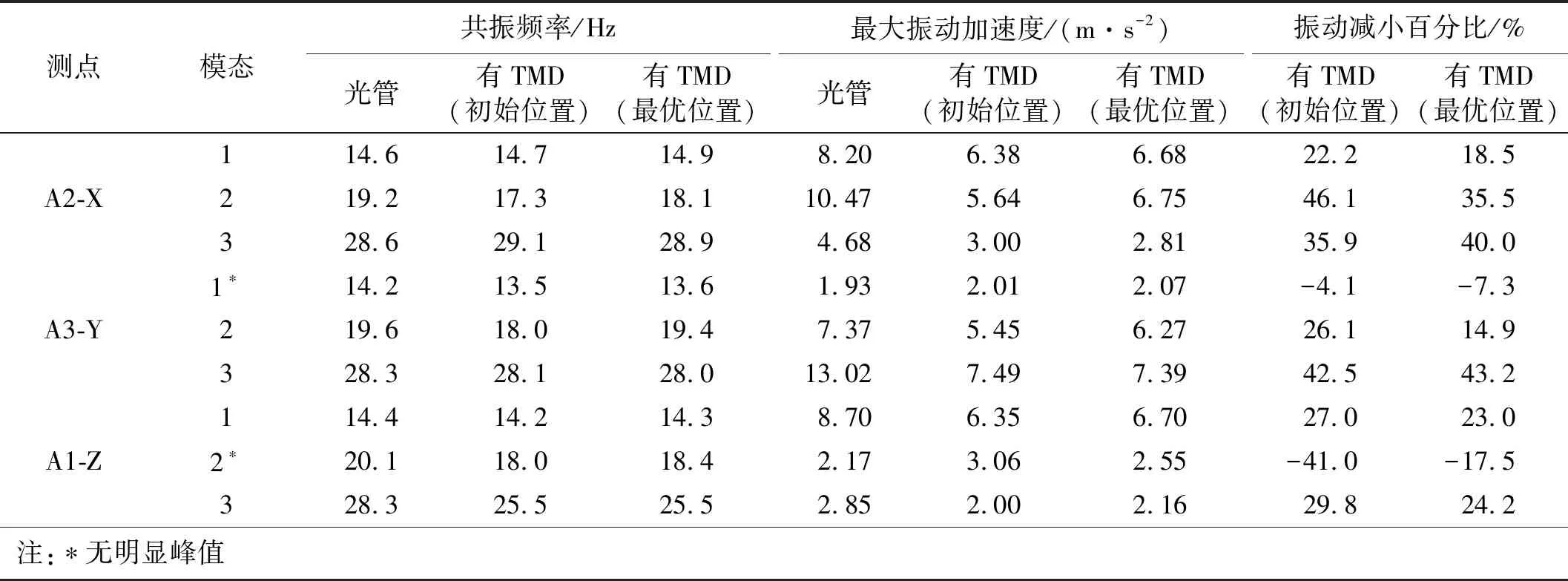
表8 减振前后最大振动加速度对比(试验)

优化方案与初始方案减振效果差异较小,因为初始位置的设置已近似为最优位置。另外,安装动力吸振器后,共振点处出现两个峰值,且两个峰值的大小相近,符合定点理论的最优同调和最优阻尼条件。而图11中仿真验证结果中,安装动力吸振器后,共振点仍然为一个峰值,原因为动力吸振器设计时计算得到的动力吸振器的所需阻尼系数偏大。

3 结 论

基于定点理论,开发设计了一款适用于三维管路的单向有阻尼动力吸振器,通过有限元仿真计算和吸振器安装位置参数优化设计,初步验证了动力吸振器的减振效果,并获取了最优安装位置,最后通过试验进行验证,得出结论如下:

基于定点理论,给出了动力吸振器关键设计参数的计算方法,并通过Visual Basic编制了参数计算器。设计的动力吸振器具有结构紧凑,稳定性好,弹性原理受力特定好的特点。

通过仿真计算,初步验证三维管路各振动响应点的减振效果在27.1%～55.8%。但是动力吸振器设计时计算得到的所需阻尼系数偏大。

但相对于未加装动力吸振器的情况,优化方案的管道振动位移响应均下降了50%以上,说明通过NSGA-Ⅱ算法开展动力吸振器安装位置优化计算具有一定可靠性。

通过试验验证发现,TMD1、TMD2和TMD3分别将各自主作用方向的振动减小23.0%、35.5%和43.2%,减振效果明显,且减振效果与仿真计算相近。