水轮机调节系统与轴系耦合模型对系统参数的敏感性分析

章志平, 张送校, 杨 雄, 秦 程, 孙 洁, 冯 陈, 张玉全

(1. 江西洪屏抽水蓄能有限公司,江西 宜春 336000;2. 河海大学 水利水电学院,南京 210098; 3. 河海大学 能源与电气学院,南京 210098)

抽水蓄能作为现阶段电力系统中最可靠的蓄能技术,它的投运可以更好地配合可再生能源大规模开发,克服风、光等清洁能源不稳定的缺点[1-2]。然而,随?着大容量、高水头、高转速水电机组的投运,水电机组的振动问题与安全稳定运行问题也日渐凸显[3]。水轮发电机组的振动问题会引发机组轴系摆度恶化,威胁着机组的发电质量、机组的寿命和安全稳定运行[4-6]。我国要继续建设、发展高质量抽水蓄能电站,推进“双碳”目标实现,就必须关注到这一问题。

在水力发电机组振动问题上,已有大量学者做出了贡献,这些研究成果主要是围绕水力发电机组轴系动力学建模展开的。如刘伟珣等[7]建立了单支撑轴系动力特性分析有限元模型,并研究了轴系对中偏差对单支撑轴系振动的影响。邹佳杰等[8]建立了水轮机流道模型与轴系模型,分析了不同负荷稳态工况下机组轴系振动的动力学特性。李建玲考虑了随机扰动、外部作用力和系统内部参数,建立了更加精确的水力发电系统非线性数学模型,并在此基础上分析了复杂外力作用下水力发电轴系的振动特性及运行稳定性。张浩[9]考虑了影响机组振动的水力、机械和电磁等因素,对水力发电系统瞬态动力学进行了建模,并深入地探究了相关的稳定性机理。Chen等[10]提出了一种基于状态空间方程的水轮机系统模型,探究了水轮机系统的非线性动力学行为。Zhang等[11]基于改进的LuGre摩擦模型,建立了考虑不平衡磁拉力、油膜力和不平衡水力激励的转子-流道-轴承系统的摩擦冲击动力学模型,揭示了磁流变液阻尼器对球泡式水力发电机组轴系振动的影响规律。

在水轮机调节系统动力学模型及其稳定性研究方面,近些年也取得了丰硕的研究成果[12-15]。如Li等[16]提出了一种改进的引力搜索算法(modified gravitational search algorithm,MGSA),提高了水轮机调节系统中的参数辨识能力。Zhang等[17]考虑了压力管内弹性水柱效应,建立了抽水蓄能水电站的线性化降阶动态模型,研究了随机负荷下PI增益对抽水蓄能电站动态特性的影响。Guo等[18]建立了一种新的随机模型来分析水力发电系统的能量分布,讨论了随机强度对水轮机运行过程中能量转换的影响。Zhang等[19-20]考虑到液压伺服系统的惯性和响应时间,将水轮机调速系统转化为快慢水轮机调速系统,研究了系统在不同时间尺度下的快慢动力学行为。

综上所述,水轮机轴系振动研究领域重点关注了影响轴系稳定性的水力因素,机械因素,和电气因素,并对相关因素的影响特性,影响因子权重进行了分析和讨论。然而,这些研究都假定机组为稳态运行,没有关注到抽水蓄能电站频繁的暂态过程对轴系振动的影响。而在水轮机调节系统的研究中,尽管关注到了暂态过程对水压力,转速的影响,但往往忽略了轴系摆度响应。在此背景下,本文以MATLAB R2021a仿真平台为研究依托,以抽水蓄能电站水泵水轮机组轴系及引水系统管道为研究对象,建立了综合考虑调节系统和轴系系统的暂态耦合模型,讨论了机组在暂态过程中的动态响应特性以及发电机偏心质量以及发电机励磁电流对轴系暂态过程的影响。本文的研究目的是建立一个完整的能够反映水电机组暂态响应的调节系统与轴系耦合模型,为水电机组的暂态研究提供理论基础。

1 水轮机调节系统与轴系耦合模型

1.1 水轮机模型

本文采用由IEEE PES Working Group on Prime Mover 提出的线性水轮机模型。其数学方程可以表示为[21]

(1)

式中,mt,qt,h,x,y分别为转矩,流量,水头,转速,导叶开度的相对偏差值。ex,ey,eh,eqx,eqy,eqh为模型系数,ex=∂mt/∂x,ey=∂mt/∂y,eh=∂mt/∂h,eqx=∂q/∂x,eqy=∂q/∂y,eqh=∂q/∂h。本文的系数取值参考石等人的取值[22],ex=-1,ey=1,eh=1.5,eqx=0,eqy=1,eqh=0.5。

1.2 调节系统模型

1.2.1 压力引水管道模型

本文假定压力引水管道长度较短,发生的水击为刚性水击,此时的压力引水管道动态特性可以表示为

(2)

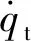
1.2.2 机组转速动态特性方程

水轮机转矩和负载力矩相互影响下的机组转速动态特性可以表示为[23]

(3)

式中:Ta和Tb分别为发电机和负载和惯性时间常数,Tab=Ta+Tb;en为综合自调节系数。

1.2.3 电液伺服系统微分方程

电液伺服系统微分方程可以表示为[24]

(4)

1.2.4 PID控制方程

PID控制方程可以写为

(5)

式中:Ty为主伺服电机时间常数;kp为比例增益;ki为积分增益;kd为微分增益。

结合1.1节的水轮机模型和1.2节的调节系统模型,水轮机调节系统的瞬态动力学模型可以表示为

(6)

1.3 轴系振动模型

1.3.1 阻尼力模型

水轮发电机组在稳定运行时,轴系受到的阻尼力可以表示为[25]

(7)

1.3.2 碰摩力模型

在碰摩力模型中,发生碰摩时认为接触点产生了法向和切向摩擦力。不考虑转子运动过程中摩擦的热效应,并假定转子与定子的碰撞为弹性碰撞,变形为弹性变形,x,y方向上的摩擦力可以表示为[26-28]

(8)

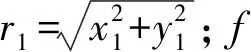
H1=0.5sign[abs(r1-δ)]+0.5sign(r1-δ)

(9)

1.3.3 电磁力不平衡模型

发电机转子不平衡电磁力是影响机组振动的重要因素之一,它诱发于发电机转子不均匀的磁场,会加剧转移偏心效应,表达式为[29]

(10)

(11)

式中:R和L分别为发电机转子半径和长度;kj为气隙基波磁动势系数,与发电机的磁极对数、匝数等有关;Ij为发电机的励磁电流;μ0为空气磁导系数;Λn为气隙磁导的fourier系数;ε为相对转子偏心量。

1.3.4 非线性油膜力模型

大扰动工况下的转子非线性动力学分析有必要考虑轴承油膜非线性的影响,假定流体不可压且黏度恒定,作用在x,y方向上的非线性油膜力如下[30]

(12)

(13)

式中:α为油膜的起始动态边界角;σ为Sommerfeld修正数;μ为油膜黏度;hoil为油膜厚度;Rb为轴承半径;Lb为轴承长度。

1.3.5 水力不平衡力模型

水力因素导致的轴系振动可能会导致过流断面存在不均匀性,造成径向水推力不平衡。由法兰密封处水流的圆周运动造成的水力不平衡力可以表示为[31]

(14)

水轮机叶片出水边开口不均匀引起的水力不平衡力可以由式(15)表示[32]

(15)

由于转轮不圆或机组轴系摆度使水封间隙周期性变化引起的压力脉动,可以表示为[33]

(16)

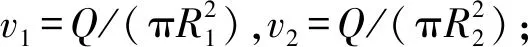
1.3.6 密封力模型

环形密封中的流体激振力表现出来的非线性特性可能会造成转子失稳。本文引入Muszynska模型表示密封力,如式(17)所示

(17)

式中:ω为转子旋转的角速度;K为密封力的当量刚度;Ds为密封力的当量阻尼;mf为密封力的当量质量;K,Ds,τf均为扰动位移x1,y1的非线性函数。

根据轴系动能和势能方程,结合1.3.1节～1.3.6节描述的作用在轴系上的由机械因素、电磁因素、水力因素引起的振动,可以得到水轮发电机轴系振动数学模型,如式(18)所示

(18)

1.4 水轮机调节系统与轴系耦合模型

机组扭矩与负荷扭矩的关系可以表示为[34]

k2(d-lsina)(x1sinωt-y1cosωt)-

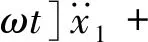
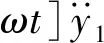
对上式进行变换,将其改写为式(19)形式

(19)

(20)

则水轮机调节系统-轴系瞬态耦合模型可以表示为

(21)

2 计算参数设置

本文采用MATLAB R2021a仿真平台进行研究,研究对象为抽水蓄能电站水泵水轮机组轴系及引水系统管道,装机容量为300 MW,额定转速为500 r/min,该电站的其他基本参数如表1所示。

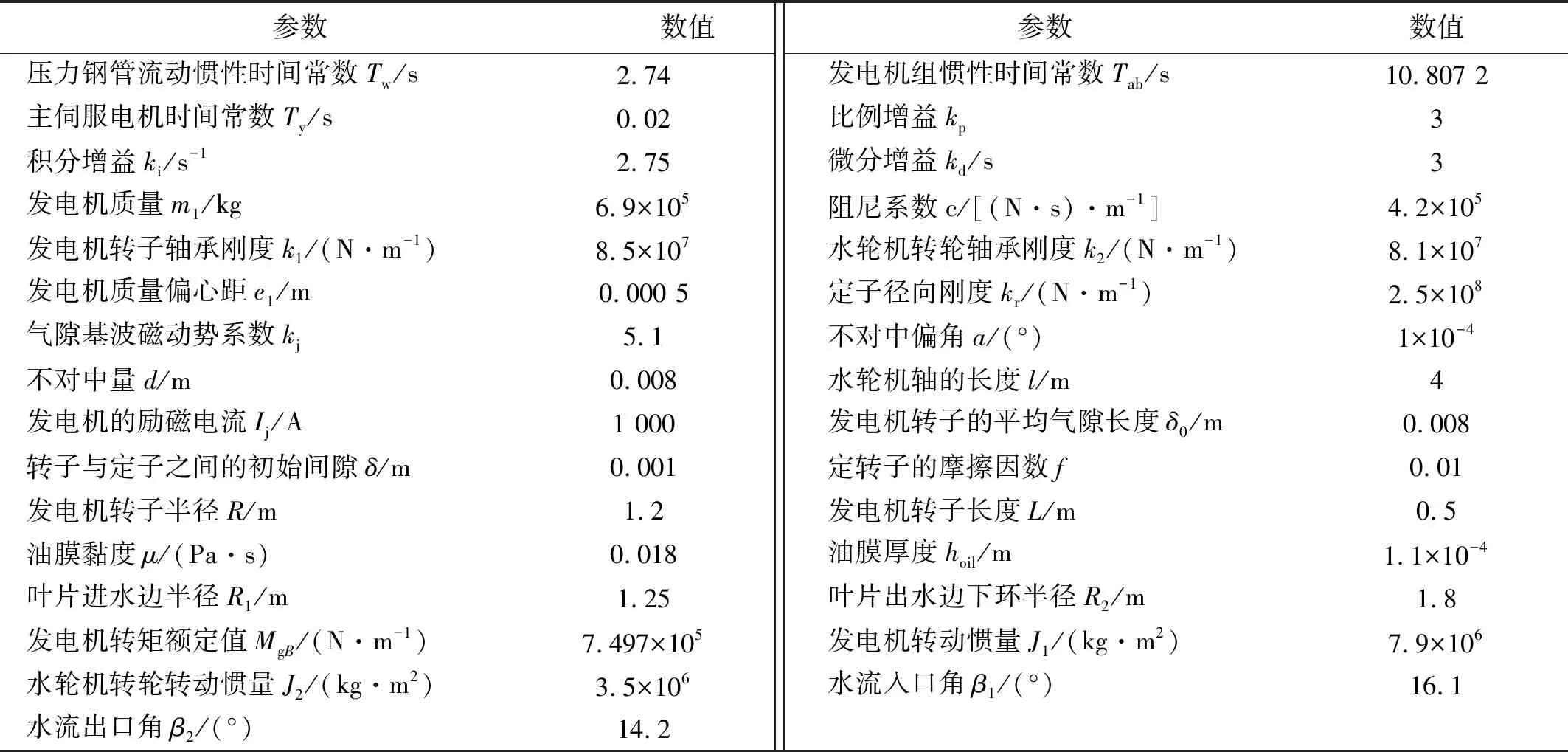
表1 电站基本参数Tab.1 Basic parameters of hydropower station

3 不同负荷扰动下的系统响应

本文计算了不甩负荷,甩30%负荷,甩60%负荷,以及甩100%负荷工况下的调节系统以及轴系系统的动态响应情况,如图1所示。根据图1(a),甩负荷后,机组的相对转速在波动若干次后收敛到平衡位置,经历的时间约为65 s。根据图1(b)～图1(f),甩负荷后,发电机转子在x方向上的振动受到了很大影响,振幅先突增,之后逐渐趋于稳定。不甩负荷时发电机转子在x方向上的振幅稳定在0.205 mm;甩30%负荷,甩60%负荷,以及甩100%负荷工况下发电机转子在x方向上的最大振幅分别为0.593 mm,0.827 mm,以及0.960 mm;再次稳定后发电机转子在x方向上的振幅则变为0.346 mm,0.429 mm,以及0.464 mm,较之负荷变化前分别增加了68.7%,109.3%,以及126.3%。图1(f)所示为发电机转子在y方向上的振动幅值变化,与x方向上的振动响应非常相似,不再赘述。

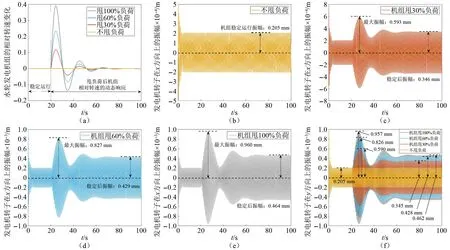
图1 甩不同负荷下调节系统及轴系系统的动态响应Fig.1 Dynamic response of regulating system and shafting system under different load rejection

4 参数敏感性分析

调节系统参数,轴系结构参数,以及运行工况参数等都会对轴系振动产生影响,本文重点分析发电机质量偏心以及发电机励磁电流变化对轴系振动响应的影响,具体见5.1节以及5.2节所示。

4.1 发电机质量偏心的影响

如图2所示是发电机偏心质量为0.4 mm,0.5 mm,以及0.6 mm时甩100%负荷后系统的动态响应变化。在甩负荷前,稳定运行下发电机转子在x方向上的振幅分别为0.099 mm,0.205 mm,以及0.342 mm,可见发电机质量偏心越小,轴系振动也越小,机组运行越稳定。甩100%负荷后,不同发电机偏心质量下振幅的最大值突增至0.892 mm,0.960 mm,以及1.042 mm;重新稳定后的振幅分别为0.373 mm,0.464 mm,以及0.589 mm。可知发电机偏心质量越大,甩100%负荷后转子的振动值也越高,轴系运行越不稳定。

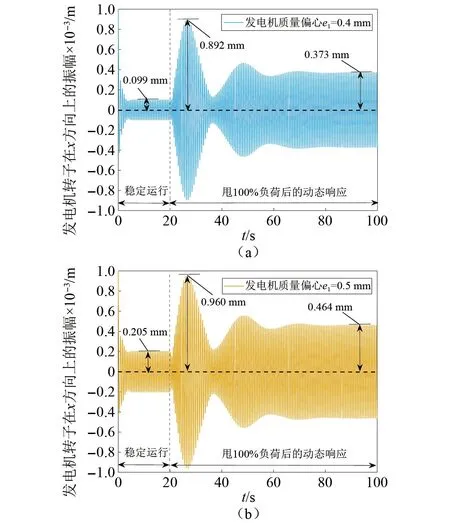
图2 发电机偏心质量变化对甩100%负荷后系统动态响应的影响Fig.2 The influence of generator eccentric mass change on the dynamic response of the system after 100% load rejection

如图3所示是不同发电机偏心质量下甩60%负荷后系统的动态响应变化。机组在稳定运行时,转子振幅与图2完全相同,当机组突然甩去60%负荷后,发电机偏心质量为0.4 mm,0.5 mm,以及0.6 mm下转子在x方向上的最大振幅分别为0.751 mm,0.827 mm,以及0.924 mm,稳定后的振幅分别为0.332 mm,0.429 mm,以及0.558 mm。图3(d)为y方向转子的振幅变化情况,可以更为直观地对比三种发电机偏心质量下轴系的响应情况。与图2相比,甩去的负荷减小,轴系响应时的最大幅值以及再次恢复稳定后的幅值也随之减小。

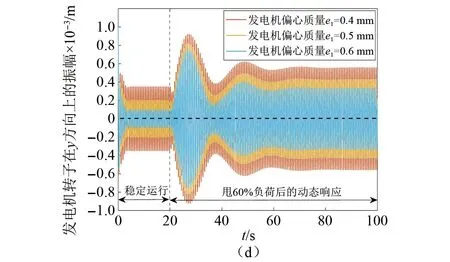
图3 发电机偏心质量变化对甩60%负荷后系统动态响应的影响Fig.3 The influence of generator eccentric mass change on the dynamic response of the system after 60% load rejection

如图4所示是发电机偏心质量为0.4 mm,0.5 mm,以及0.6 mm下甩30%负荷后系统的动态响应。甩负荷后,不同偏心质量下的最大幅值分别达到了0.501 mm,0.593 mm,以及0.715 mm;稳定后的幅值分别为0.248 mm,0.346 mm,以及0.481 mm。由图2、图3、图4可知,当发电机偏心质量一定时,甩去的负荷越多,动态响应过程中幅值的波动越大,轴系运行越不稳定;当甩去的负荷一定时,发电机的偏心质量越大,水轮发电机组轴系在动态响应过程中的幅值越高,这会给系统稳定运行带来挑战和隐患。

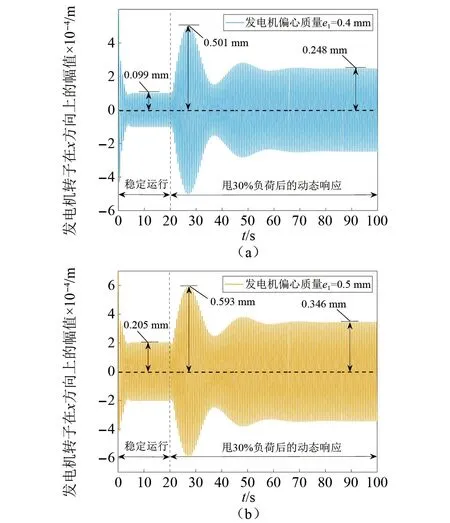
图4 发电机偏心质量变化对甩30%负荷后系统动态响应的影响Fig.4 The influence of generator eccentric mass change on the dynamic response of the system after 30% load rejection

4.2 发电机励磁电流的影响

如图5所示是发电机励磁电流为800 A, 1 000 A, 1 200 A时,甩100%负荷后发电子转子在x方向上的动态响应的过程。在甩负荷前,励磁电流越大,转子的振幅越小,在800 A, 1 000 A, 1 200 A下的转子振幅分别为0.254 mm,0.205 mm,以及0.147 mm。突然甩掉100%负荷后,其最大振幅突增至0.984 mm,0.960 mm以及0.857 mm,励磁电流越大,突增后的幅值越小。轴系再次稳定后,振幅也停止波动,分别稳定在0.549 mm,0.464 mm,以及0.346 mm。图5(d)描述了y方向上的动态响应,可以看出较大的励磁电流更有利于机组稳定运行。

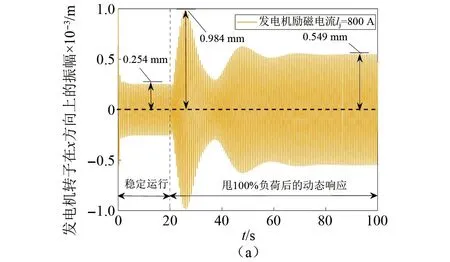
图5 发电机励磁电流变化对甩100%负荷后系统动态响应的影响Fig.5 The influence of generator excitation current change on the dynamic response of the system after 100% load rejection

图6为甩60%负荷后不同励磁电流下发电子转子的径向振动响应情况。在800 A, 1 000 A, 1 200 A下,x方向上的最大振幅达到0.865 mm,0.827 mm,以及0.692 mm,暂态过程结束后的振幅分别稳定在0.512 mm,0.429 mm,以及0.318 mm。与图5相比,当甩去的负荷变少,轴系振动的幅值也变小,机组运行变得更加稳定。

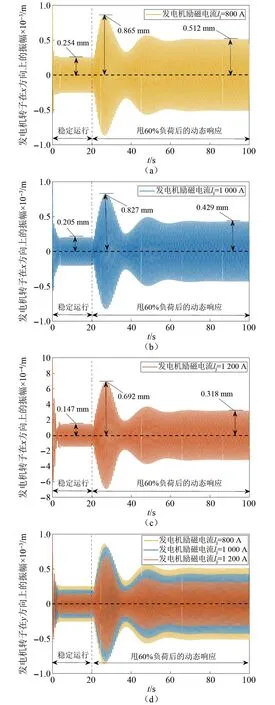
图6 发电机励磁电流变化对甩60%负荷后系统动态响应的影响Fig.6 The influence of generator excitation current change on the dynamic response of the system after 60% load rejection

图7是发电机励磁电流变化对甩30%负荷后系统动态响应的影响。x方向的最大振幅在800 A, 1 000 A, 1 200 A下分别达到了0.659 mm,0.593 mm,以及0.457 mm,稳定后的振幅分别达到了0.420 mm,0.346 mm,以及0.252 mm。根据图5～图7可以发现,甩相同负荷时,励磁电流越大,轴系在响应过程中的幅值越小,越有利于系统稳定运行。

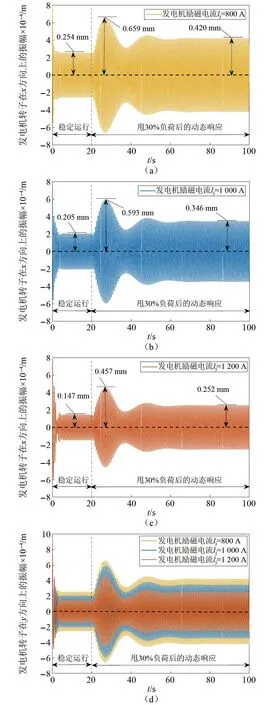
图7 发电机励磁电流变化对甩30%负荷后系统动态响应的影响Fig.7 The influence of generator excitation current change on the dynamic response of the system after 30% load rejection

5 结 论

本文建立了水轮机组调节系统与轴系系统的瞬态耦合模型,分析了机组甩负荷下轴系的振动响应情况,探讨了耦合模型对质量偏心、励磁电流的敏感性。得到的结论如下:

(1) 甩负荷后,机组的相对转速在波动若干次后收敛到平衡位置,经历的时间约为65 s,发电机转子的振幅先突增,在经历短暂波动后逐渐趋于稳定。

(2) 甩30%负荷,甩60%负荷,以及甩100%负荷工况下发电机转子在x方向上的最大振幅分别为0.593 mm,0.827 mm,以及0.960 mm;再次稳定后发电机转子在x方向上的振幅较负荷变化前分别增加了68.7%,109.3%,以及126.3%。

(3) 当甩去的负荷一定时,发电机的偏心质量越大,水轮发电机组的轴系在动态响应过程中的幅值越高,这会给系统稳定运行带来挑战和隐患;而励磁电流越大,轴系在响应过程中的幅值越小,越有利于系统稳定运行。当发电机偏心质量以及励磁电流一定时,甩去的负荷越多,动态响应过程中幅值的波动越大,轴系越不稳定。