核电工程异形水箱流固耦合分布式参数模型与效用研究

李建波, 刘 佳, 李志远, 林 皋

(1. 大连理工大学 海岸与近海工程国家重点实验室,辽宁 大连 116024;2. 大连理工大学 建设工程学院,辽宁 大连 116024;3. 中国水利水电科学研究院 工程抗震研究中心,北京 100048)

2011年日本福岛核事故后,核电结构的抗震分析模型变得日益精细化和体系化。在土-结构相互作用框架下,液体和屏蔽厂房之间的流固耦合效应成为结构抗震分析的重要组成部分。许多学者基于精细模拟对异形水箱的流固耦合问题开展了深入研究,发现了结构形状对液体的晃动特性有显著影响。

在核电结构异形水箱的流固耦合仿真分析中,主要有两种思路:一是基于声学-结构耦合法(Acoustic-Structural coupling,CAS)、光滑粒子流体动力学(smoothed particle hydrodynamics, SPH)[1]、耦合欧拉-拉格朗日(coupled Eulerian-Lagrangian,CEL)法[2-3]等精细模拟液体和器壁动力耦合相互作用的耦合数值模型;二是以附加质量表征流体动力学特征的集总参数模型,如在有限域水体中的Housner等[4-5]模型和无限域水体中基于Westergarrd[6]公式的动水附加质量模型。

虽然前者更为精细,但是具有建模复杂、求解耗时长等缺陷,并且其分析过程与输入地震动密切耦联,不适用参与复杂条件的工程计算。此外,与CAS法相比,虽然SPH和CEL方法能够反映液体的形态,但由于流固耦合的特殊性,它常常导致土结构相互作用在稳定性方面出现严重问题,在CEL法中泄漏问题是经常遇到的情况,SPH法的计算精度偏低,计算耗时。因此,在流固耦合中CAS法是基于有限元的较为常用数值模拟方法,此外还有边界元法[7]、比例边界有限元法[8]等边界类数值方法,都在流固耦合分析中也取得了进展。需要指出的是,边界元法和属于比例边界有限元法本质上仍然属于全耦合求解过程。

在以工程结构设计为目标的抗震分析通常使用一种标准化的稳定附加质量模型,在核电领域中也应该建立相匹配的标准化模型方法。虽然核电抗震设计规范中推荐使用Housner模型,但传统的Housner附加质量模型主要有两方面不足:一方面,Housner模型只有在刚性器壁下截面规则的断面才能得到稳定解析解;另一方面,集中式附加质量模型只能反映整体效应,导致在局部应力分析中存在明显不足。目前通过将波函数方法直接应用于Housner模型的推导公式,最终得到分布式质量模型[9]。如黄文等[10]利用Housner模型和流固耦合方法计算了圆柱形容器中的地震响应。宝鑫等[11-12]在Housner附加质量模型的基础上研究了环形水箱、底部为锥形和圆柱形的PCS水箱,并给出了其经验公式。

除以上方法,还有基于精细模拟流固耦合模型直接提取动水压力的计算结果[13]将其转化为附加质量的方法,但这种方法面临在不同的激振信号下结果具有不确定性的问题。综上所述,虽然等效附加质量的求解方式繁多,但Housner模型的基本建模思路仍然占据主要地位。

目前在流固耦合领域剥离附加质量模型主要存在两个问题:其一是解耦动水附加质量与激励地震动变量之间的解耦问题;其二现有的等效附加质量模型中常常忽略动水附加质量中的对流质量,而对流质量会对计算结果产生不确定性的影响[14]。

本文基于模态综合法[15]提出一种复杂水箱的流固耦合分析方法,并且解耦动水质量与加速度激励之间的关系,获得了稳定的动水分布质量模型,并将其应用于核电异形水箱。模型具有以下特点:第一,从异形水体动力特性的理论角度出发,将流固耦合界面的动水压力描述成动水压力与地震激励相乘的形式,剥离附加质量与地震激励的耦联关系。第二,晃动质量不再在整体器壁上进行积分,而是在各个点的控制处进行积分。同时,冲动质量的定义也发生了变化,它使用该层水体和其差值来定义,而不再使用总体差值来进行分摊,使得模型更加精确和准确。本模型通过与精细有限元模拟模型进行验证,证实了该模型的准确性和有效性;同时,针对不同水位情况和不同格栅工况下非能动水箱的响应和减震作用进行了研究,得出了非能动水箱的较佳水位和格栅分布,为水箱的抗震和减晃措施研究提供了一种有效手段。

1 流固耦合分析的分布质量模型

1.1 液体对器壁的动水压力

假定容器器壁为刚性,液体不可压缩、无黏、无旋。以速度势函数Ф(x,y,z,t)为变量的控制方程及结构交界面、自由液面的边界条件为

(1)

(2)

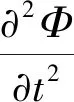
(3)

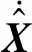
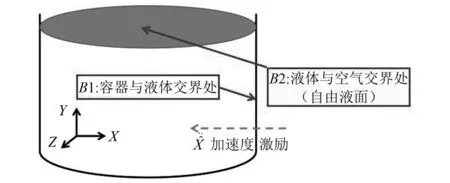
图1 水平激励下的任意形状液体容器Fig.1 Liquid container of arbitrary shape under horizontal excitation

(4)

在液固耦合分析中,通过设置不同的边界条件可将液体动水压力分解为与器壁共同运动的脉冲分量和液体自由振动的对流分量。对于包括脉冲分量和对流分量的总动水压力,自由液面处的边界条件由伯努利方程确定,即z=HL处的动水压力为

p=ρLgh

(5)

式中:HL为液体深度;h为液面离开自由液面静止位置的垂直位移。当不考虑液体自由振动的对流分量时,在水平激励作用下液体与器壁共同运动,在自由液面不会产生竖向运动,则z=HL处的动水压力为

p=0

(6)

求解式(1)～式(6)可以得到储液容器内任意位置处的动水压强p。将势函数Φ分解成与液体晃动相关的运动势ΦS和与液体脉动相关的冲动势ΦU。液体对侧壁总的动水压力可表示为

(7)

基于刚性器壁假定,冲动势ΦU函数可表示为器壁速度的线性函数。因此,求解动水压力的问题关键为求解运动势函数ΦS。

在分析域Ω上对ΦS的边界条件和运动方程进行变分并使用格林函数进行化简,可得控制方程

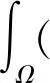
(8)

式中,φ*为权函数。液体的对流分量体现液体自由振动运动,因此ΦS可表示为液体自由振动模态的叠加

(9)

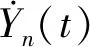
(10)

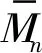
(11)

(12)

求解式(10)可以得到振型的广义坐标Yn(t),代入式(9)中可得对流势函数,代入式(7)可得液体对器壁的动水压力。

1.2 流固耦合的分布质量模型

式(7)、式(11)和式(12)均为积分方程,对于简单规则形状的容器可直接求解,但对于异形水箱无法直接计算。针对异形水箱,采用对容器侧壁进行有限元离散,对液面下的每个侧壁单元上的动水压强积分,可以得到这个单元上承担的动水压力值

(13)

式中,s为离散单元的面积。根据等参变化,式(13)的积分可在母单元的局部坐标下计算,通过雅可比矩阵将参变量转换到实际单元中。

为了更加直观地表示对流质量和脉动质量,将对流质量对应的广义坐标采用液体晃动相对运动来表示。定义变量

(14)

水体相对于水箱晃动的相对位移表示为

(15)

则对应的液体对侧壁的动水压力表示为

(16)

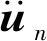
(17)

(18)

每个节点处的等效脉冲质量和对流质量可通过,节点控制面积与单元面积的比值进行求解。至此对于任意形状储液容器液体的动水压力分析,可以等效为分布式的对流质量和脉动质量,从而对复杂的流固耦合问题进行解耦并有效的提高计算效率。

1.3 基于建立模型流固耦合分析的计算流程

本文提出的基于分布式等效附加质量的流固耦合解耦模型,自主开发了相应程序,实现了液体脉冲质量、对流质量以及弹簧常数的自动计算和添加,及动力求解等功能。计算流程图如图2所示,基于提出模型的流固耦合分析主要包括两个步骤:①对液体进行有限元建模,利用自编程序计算附加质量;②将附加质量以弹簧质量单元施加到结构整体模型中,进行地震动力计算。

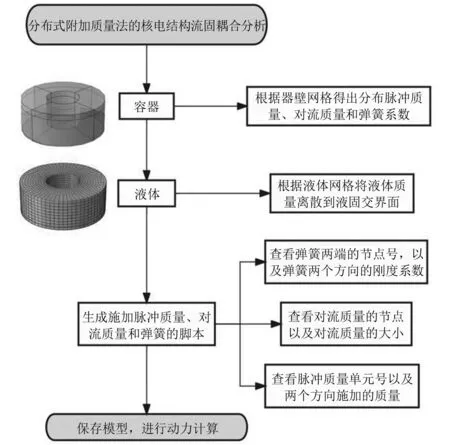
图2 分布式质量简化模型计算流程图Fig.2 Calculation flow chart of distributed mass simplified model

2 分布式质量模型的验证与讨论

2.1 圆柱形水箱的自振频率及动水压力

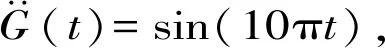
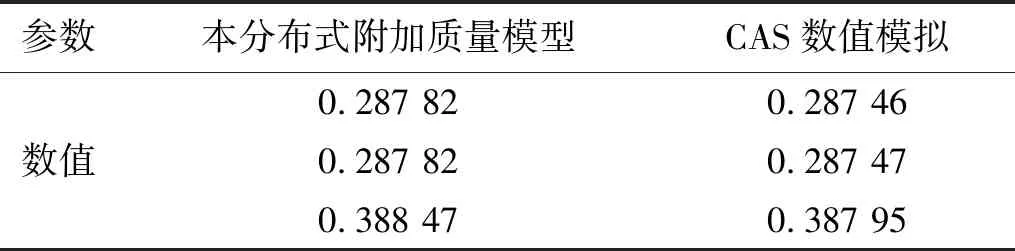
表1 前3阶振型的固有频率

为了验证声学-结构耦合法和分布式附加质量法的合理性,在圆柱形平底水箱的情况下提取了位于水箱中部位置的动水压力,并将其与Housner模型[16]的结果进行对比,如图3所示。由图3可知,本文提出的分布式附加质量模型和CAS模型在分析规则圆柱形水箱时产生的等效压力结果与Housner模型的结果是一致的,这进一步验证了这两种方法的合理性。

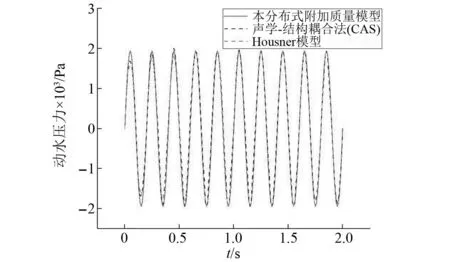
图3 距自由液面2 m处动水压力时程曲线Fig.3 Time history curve of dynamic water pressure 2 m away from the free liquid surface

2.2 PCS水箱的自振频率及动水压力

李建波等建立的AP1000模型如图4所示,重力水箱在核电厂屏蔽厂房的顶部,质量约3 000 t,正常运行水深为9.8 m。安全壳材料采用C40标号混凝土,质量密度为2 400 kg/m3,泊松比0.17,弹性模量3.25×104MPa;液体部分密度为1 000 kg/m3,剪切模量1.96 GPa。PCS水箱和结构厂房的尺寸如表2所示。

表2 材料参数表Tab.2 Material parameter table

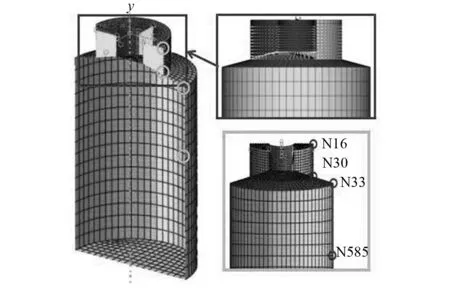
图4 AP1000 PCS有限元模型剖面图和关键点示意图Fig.4 AP1000 PCS finite element model and profile Schematic diagram of key points

结构的模态和频率是结构的固有特性,为验证此分布式附加质量模型的正确性以及其精度,将本模型与流固耦合分析中常用的CAS数值模拟的前3阶振型的固有频率(Hz)相对比如表3所示。

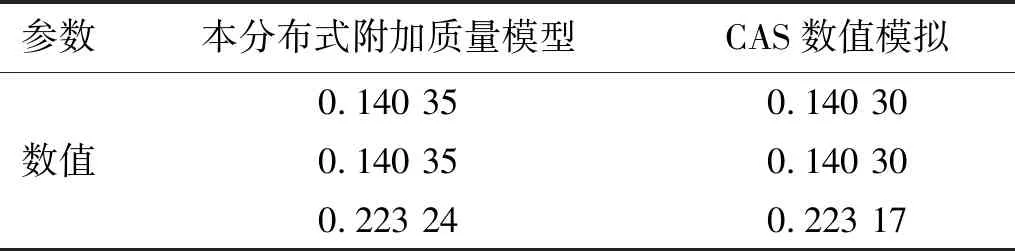
表3 前3阶振型的固有频率

根据法规标准谱RG1.60[17-18]合成地震波加速度时程输入,持续时间为27.99 s,时间步长为0.01 s,加速度峰值为0.3g。由1.2节的计算得到的脉冲质量和对流质量,以弹簧阻尼器和附加质量的形式施加在AP1000顶部的水箱侧壁和斜底面,进行动力求解计算。

提取位于水箱中部位置的动水压力,如图5所示。不难看出,本文分布式附加质量模型与CAS模型所产生的等效压力具有较好的一致性。

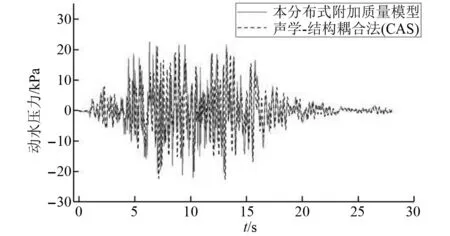
图5 距自由液面3 m处动水压力时程曲线Fig.5 Time history curve of dynamic water pressure 3 m away from the free liquid level

2.2.1 计算效率

为了比较两种方法的计算效率并确保计算时间的可比性,以上的计算分析都在同一台计算机上进行。该计算机的配置如下:内存容量为32 G,CPU主频为2.61 GHz,拥有6核12线程。在相同的安全壳网格划分下,不同计算所需的时间如表4所示。

表4 两种方法计算时间比较

CAS模型的计算时间相较于附加质量模型高出一倍。分析其主要原因有两点:首先, CAS模型在计算过程中需要同时处理液体网格,导致计算量显著增加;其次,CAS模型需要同时考虑液体和器壁之间的接触关系,在判断边界条件时需要耗费大量时间。因此,本文提出的分布式附加质量模型在计算效率上明显优于CAS模型,显著提升了求解效率。

2.2.2 结构响应的加速度时程

对核岛结构进行动力计算并提取两种计算方法的3个观测点在RG1.60地震动下的加速度时程响应结果如图6～图8,在地震动下加速度响应峰值对比如表5所示,并分析两个模型计算结果的相对误差。

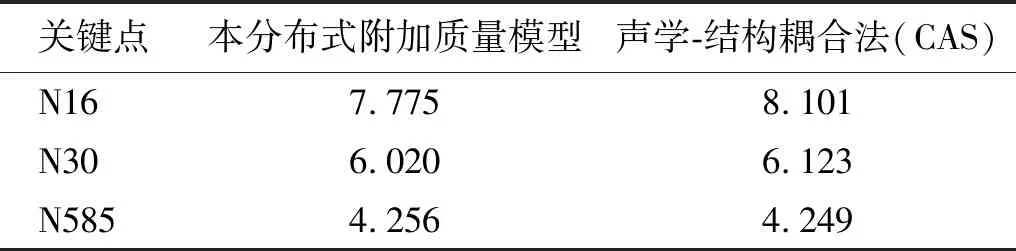
表5 RG1.60地震下加速度峰值对比

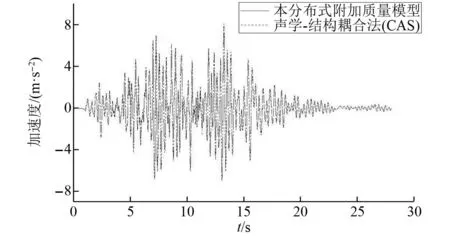
图6 观测点N16加速度时程Fig.6 Observation point N16 acceleration time history

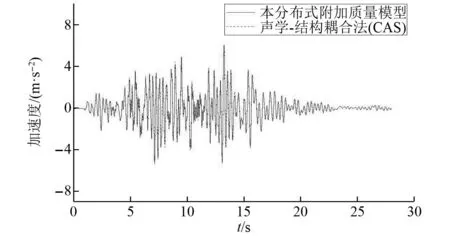
图7 观测点N30加速度时程Fig.7 Observation point N30 acceleration time history

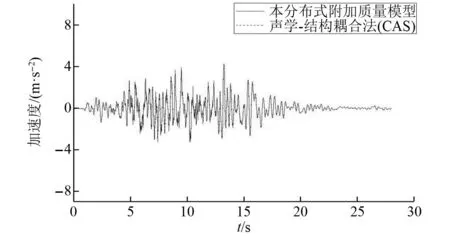
图8 观测点N585加速度时程Fig.8 Observation point N19 acceleration time history

通常在箱线图中样本数据超出上边缘线和下边缘线的概率低于0.7%,故使用箱线图可以极好地反映各点加速度响应相对误差的离群程度,并且此种统计方法将误差分析从峰值点拓展到全时程。

如图9所示3个观测点中各点加速度响应的相对误差最大值都小于4%,本分布式附加质量模型在保证理想计算精度的条件下,节省了计算时间,极大地提高了计算效率,证明了本分布式附加质量模型与CAS计算模型在模拟结果中的高度一致性。

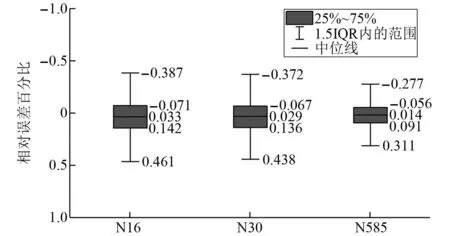
图9 误差箱线图Fig.9 Error box diagram

2.2.3 结构响应的楼层谱

根据加速度反应的时程曲线计算得出楼层反应谱,图10～图12列出了AP1000模型在地震动激励下3个观测点的楼层反应谱情况,在水平方向激励下两种计算模型的反应谱曲线在各个频段基本吻合。为了更清楚地反映其差异大小,图13绘制了3个观测点楼层反应谱的误差箱线图。由箱线图可以得出在100 Hz以内所有频率点中绝大部分的误差都小于5%,说明两种计算模型结果具有一致性。

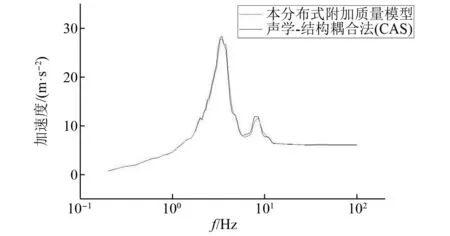
图10 观测点N16反应谱对比Fig.10 Observation point N16 acceleration time history

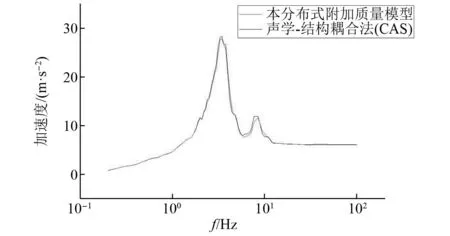
图11 观测点N30反应谱对比Fig.11 Observation point N30 acceleration time history

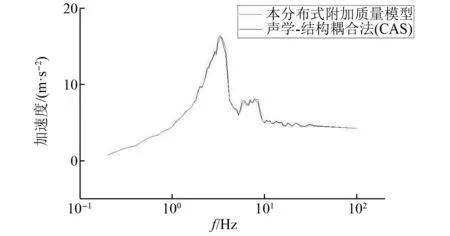
图12 观测点N585反应谱对比Fig.12 Observation point N19 acceleration time history

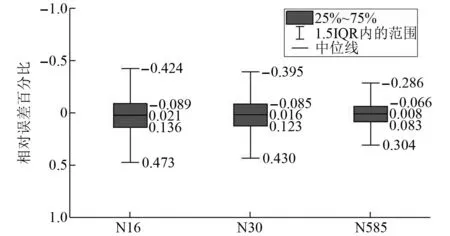
图13 误差箱线图Fig.13 Error box diagram

2.2.4 安全壳应力包络图

图14为本分布式附加质量模型和CAS计算模型所计算得到的安全壳最大Mises应力包络分布云图。由图14可知,两种方法计算得到的包络云图分布基本一致,两种计算方法所得到的最大Mises应力值均出现在安全壳侧壁转角的位置,即为安全壳应力包络图红色部分所示。其中声学-结构耦合(CAS)法所得到的最大值为55.11 MPa,本分布式附加质量模型的应力最大值为53.73 MPa,相对误差为2.50%。在考虑流固耦合效应的实际工程应用中,应在安全壳侧壁转角处以及安全壳底部充分考虑安全裕度。

图14 本分布式附加质量模型(左)与声学-结构耦合(CAS)计算模型(右)最大Mises应力分布图Fig.14 Distributed additional mass model (left) and Acoustic-structural coupling (CAS) calculation model (right) maximum Mises stress distribution

2.3 分布式附加质量的讨论

通常在动水压力中对流质量的占比较小,由于核电结构精细模拟的必要性,在核电结构设计中仍然考虑对流质量。

图15和图16给出了脉冲质量和对流质量随液体高程分布图。图15中曲线①表示水箱内壁的脉冲质量随高程的分布,曲线②表示水箱外壁的脉冲质量分布。

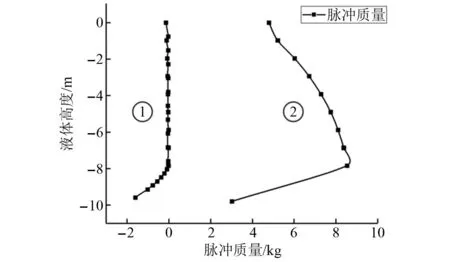
图15 脉冲质量随高程分布图Fig.15 Pulse mass distribution with elevation

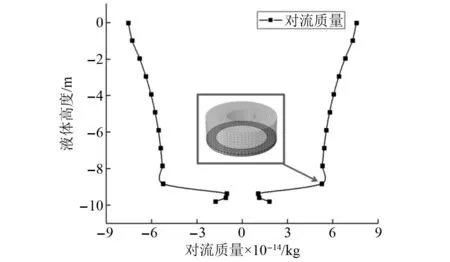
图16 对流质量随高程分布图Fig.16 Distribution of convective mass with elevation

本分布式附加质量模型克服了经典Housner模型的局限性,将规则水箱的求解拓展到了不规则水箱。

为得出附加质量沿容器圆周分布的规律,获取从X轴正向逆时针偏转30°、60°、90°的脉冲质量,如图17所示。可以得出最大质量值截面在X轴0°方向上,并且随着偏转角度的增加,各截面的沿高程分布的附加质量值逐渐减少。当截面旋转到图17中圆形图例截面位置时,该位置上附加质量接近于0。

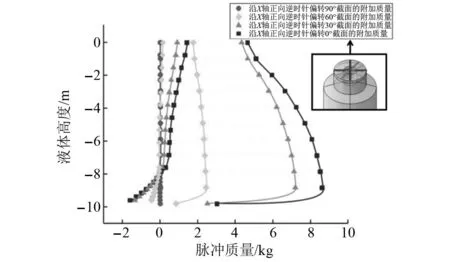
图17 附加质量随高程分布图Fig.17 Additional mass distribution map with elevation

3 AP1000安全壳动力响应的规律讨论

异形水箱的不规则性主要体现在以下两点:截面的不规则性和网格划分的不规则性。在面临液体内有夹杂的复杂工况时,例如容器存在减震格栅、容器内部存在异种液体分层、容器边角倒角等情况,本文以格栅为代表进行探讨,计算不同数目格栅情况下的加速度响应以及倾覆力矩等。

网格划分的不规则性主要出现在对容器内部液体的网格中,一般在规则水箱中的液体网格划分以六面体为主,很少出现不规则的网格。但是在不规则容器中,液体内部可能出现四面体单元。在参考文献[15]中只对圆柱形平底水箱进行了数值分析验证,本文将其推广到了异形水箱,并使用有限元的方法建立附加质量模型可以基于四面体单元进行离散,解决网格划分不规则性的问题。

3.1 水位对AP1000安全壳结构响应的影响

图18设定了AP1000水箱三种不同水位的示意图,其中图18(a)为高储液率水位,取水位值为9.8 m;图18(b)为中储液率水位,取水位值为4.9 m;图18(c)为低储液率水位,取水位值为2.45 m。

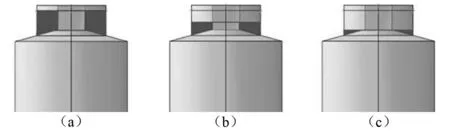
图18 AP1000模型水箱不同水位工况示意图Fig.18 Schematic diagram of different water levels of AP1000 model water tank

图19给出了三种储液率工况下的附加质量分布图。图20给出了不同水位工况下AP1000安全壳不同高度点的峰值加速度在RG1.60地震作用下的变化情况,在AP1000顶点(N16)的加速度响应随着水箱水位的降低表现为逐渐增大的变化规律,从高储液率下降到中储液率时增加幅度较不明显,但中储液率下降到低储液率时增加幅度较大。在AP1000结构中部位置(N30和N33),中储液率的峰值加速度高于高储液率和低储液率工况的峰值加速度,随水箱水位高度的变化规律表现为先增大再减小。在AP1000结构中下部位置(N585)在各个水箱水位工况下的峰值加速度变化幅值不大,规律变化也表现为先增大再减小。水箱的液体确实在一定程度上起到了降低加速度响应的作用,如表6所示。

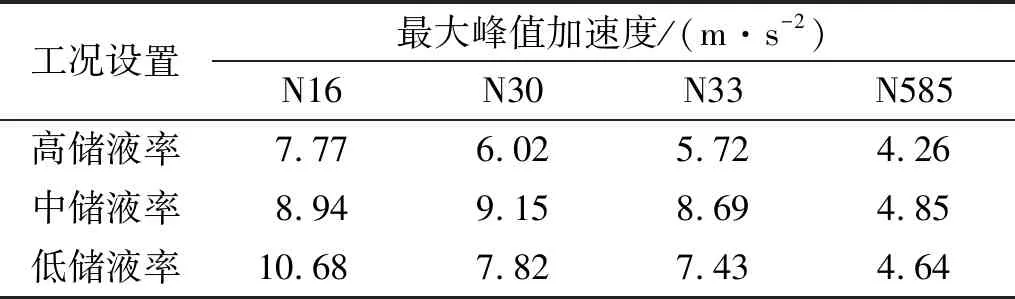
表6 RG1.60地震下加速度峰值和水位高度的关系

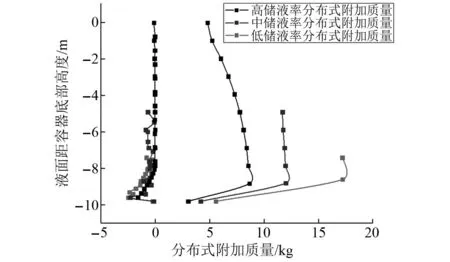
图19 不同水位工况下的附加质量分布图Fig.19 Additional mass distribution maps under different water level conditions

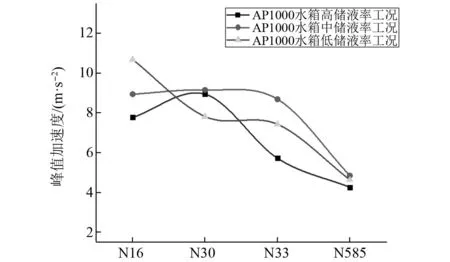
图20 RG1.60下加速度峰值和水位高度的关系Fig.20 Relationship between peak acceleration and water level at RG1.60

3.2 格栅对AP1000安全壳结构响应的影响

当核电工程遭遇地震作用时,PCS重力水箱中的动水压力对结构造成不利影响甚至导致水箱破坏,因此抑制液体晃动的格栅具有极高的实际应用价值[19-20]。四格栅和八格栅AP1000水箱示意图,如图21所示,在工况设计中将格栅高度考虑为从容器顶部连接到容器底部,同时水箱水位都假定为9.8 m。

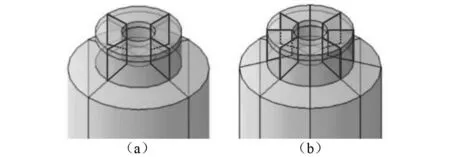
图21 AP1000模型水箱四、八格栅图Fig.21 AP1000 model water tank four, eight grid diagram

图22给出了三种不同格栅数目工况下的附加质量分布图。图23表示AP1000安全壳不同观测点位置与不同格栅工况的峰值加速度之间的变化关系。在AP1000顶点(N16)的加速度响应随着格栅数量的增加表现为减小-增加的变化规律。格栅数量从无格栅增加到四格栅时峰值加速度降低,格栅数量从四格栅增加到八格栅时峰值加速度增加。

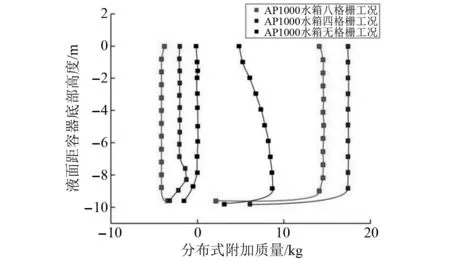
图22 不同格栅数目下的附加质量分布Fig.22 Additional mass distribution under different number of grilles

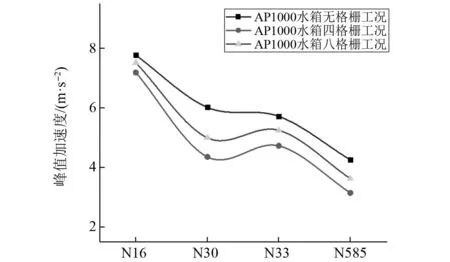
图23 RG1.60下加速度峰值与格栅数量的关系Fig.23 Relationship between peak acceleration and number of grilles at RG1.60

在AP1000结构中部位置(N30和N33),中储液率的峰值加速度高于高储液率和底储液率工况,随水箱水位高度的变化规律表现为先增大再减小。在AP1000结构中下部位置(N585)在各个水箱水位工况下的峰值加速度变化幅值不大,规律变化也表现为先增大再减小。表7可得出在水箱内部布设一定数目的格栅能在一定程度上能降低加速度响应,在计算的三种格栅数目工况中四格栅表现最佳。

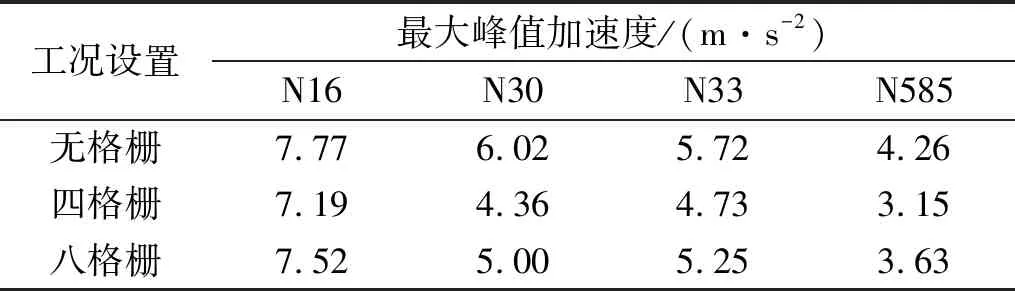
表7 RG1.60地震下加速度峰值与格栅数量的关系

4 结 论

本文提出了一种适用于异形水箱的液体晃荡动力性质模拟的分布式质量简化模型,这一模型能够有效地克服传统的Housner模型仅适用于规则水箱,且过于强调整体水体晃动效应的局限性。

从理论中基于势流理论和模态综合法进行分析,不仅适用于不规则水体形状,而且有效分离了液体晃动特征与激振条件之间的耦合作用。在数值方面,通过与精细流固耦合模型进行比较,验证了该模型具有良好的精度。

从工程实践中围绕核电异形水箱的液固耦合动力响应分析,在不同水位及采用不同数量的格栅减晃措施下,容器壁的动力响应反映出显著的差异,说明本文模型在工程适用性方面具有较好的参数敏感性特征,并对工程的优化设计问题具有一定的参考作用。