公钥加密综述*

陈 宇, 易红旭, 王煜宇

1.山东大学 网络空间安全学院, 青岛 266237

2.密码科学技术全国重点实验室, 北京 100878

3.山东大学 密码技术与信息安全教育部重点实验室, 青岛 266237

4.电子科技大学, 成都 611731

1 引言

密码几乎与文字一样古老, 发展历程大概可以分为以下两个阶段:

• 古典阶段: 该阶段的密码内涵局限于加密方案.在古典密码早期, 密码就已经广泛应用于战争的机密通信中, 密码方案的安全性依赖于对其本身的保密, 最为著名的是Caesar 密码, 其本质是将字母循环后移三位进行简单的单表代换加密.在古典密码中期, 密码的安全性摆脱对于系统保密性的依赖, 转向对密钥的保密, 代表性的方案是多表代换加密的Vigènre 密码, 其不断重复密钥并与加密消息进行相加.在古典密码后期, 人们进一步发展Caesar、Vigènre 等简单代换、置换密码的设计思想, 设计出古典密码的巅峰代表Enigma 密码, 其代换规则是动态的, 每加密一个字母的消息后, 随着内部诸多转子的位置变化, 代换规则动态地改变, 从而使得代换、置换关系更为复杂.总的来说, 古典阶段的密码通常由代换和置换构成, 缺少系统的设计方法论, 一旦加密方案暴露, 容易受到密码分析而被攻破, 从而陷入了“攻破-修复” 的循环, 密码的设计更类似于一种“艺术”, 而非“科学”[1].

• 现代阶段: 现代阶段的早期, Shannon 在著名论文《密码学的数学理论》[2]首次使用概率论的方法对密码系统的安全性进行了精准刻画, 奠定了现代密码学的基础, 使得密码学从“艺术” 走向“科学”.随着信息化的加速, 密码也从军用扩展到商用和民用, Feistel 基于可逆计算的概念设计了Feistel 密码体系[3], 该体系在对称密码的理论和实践上都占据重要地位, 对称密码的设计与分析逐渐形成较为系统的方法, 对称密码标准DES (data encryption standard) 应运而生; 现代阶段的中期, 计算设备的算力飞速提升、计算环境由集中式迁移到分布式, 信息技术的迅猛发展对密码学提出了新的挑战.1976 年, Diffie 与Hellman 发表了著名的论文《密码学的新方向》[4], 其中蕴含的“不对称” 思想标志着公钥密码学的诞生.Goldwasser 和Micali[5]给出了公钥加密的合理安全性定义—语义安全, 构造出了满足语义安全的概率公钥加密方案, 并在此过程中开创了可证明安全的方法, 即借助计算复杂性理论中的归约技术将密码系统的安全性严格归结为计算困难问题的困难性.此后, 密码学蓬勃发展, 内涵不断丰富, 从加密、签名和密钥交换扩展到零知识证明[6]、安全多方计算[7]等.2000 年以后至今, 信息化技术进一步高速发展, 面对更为多样的应用需求和更强的攻击手段, 函数加密、全同态加密等高功能密码方案和抗泄漏、抗篡改等高等级安全相继出现[8].总的来说, 区别于古典阶段密码设计的“随意的艺术”, 现代密码学与计算复杂性理论结合更为紧密, 建立起丰富的归约网络[9], 强调形式化的定义、准确的计算困难假设和严谨的可证明安全的技术框架.

本文将按照安全性增强和功能性扩展这两条并行的线索对公钥加密的发展历程和前沿进展做系统综述.在密码学的发展历程中, 当具有新的功能性或安全性的方案被提出后, 密码学家通常先给出若干具体方案, 然后随着研究的深入再抽象出更基本的密码原语, 进而以它们为底层组件给出通用构造.通用构造不仅能够总结一般的方法对既有方案进行分类, 还能凝练关键的思想从而加深对密码方案本质的认识、启发新的构造, 因此极具价值.为了引领读者从更高的观点回顾公钥加密, 本文注重对通用构造的介绍, 其中所涉及的底层密码原语将有助于读者拓展知识面、加深理解认知.

2 预备知识

2.1 符号与记号

对于自然数n ∈N,[n]表示集合{1,2,···,n},Zn表示集合{0,1,···,n−1},Z∗n表示集合{x ∈Zn|gcd(x,n) = 1}.对于集合X,|X| 表示其大小; 对于变量x,|x| 表示其二进制表示长度.xR←−X表示对集合X进行随机采样, 得到元素x.本文使用λ ∈Z+表示安全参数.如果关于λ的函数小于任意关于λ的多项式的逆, 则称其是可忽略的(记作negl); 如果一个随机算法的运行时间由关于λ的多项式函数界定, 则称其是概率多项式时间的(记作PPT).

2.2 公钥加密的定义与安全性

Diffie 和Hellman[4]在1976 年的划时代论文中正式提出公钥加密(public-key encryption, PKE),其与对称加密的根本差别在于每个用户自主生成一对密钥, 公钥用于加密、私钥用于解密, 发送方仅需知晓接收方的公钥即可向接收方发送密文.

定义1 (公钥加密方案) 公钥加密方案由以下四个PPT 算法组成(如图1 所示):

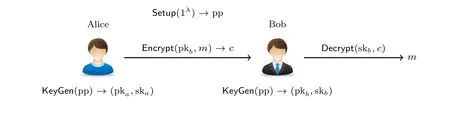
图1 公钥加密方案示意图Figure 1 Schematic diagram of public-key encryption scheme

• Setup(1λ): 系统生成算法以安全参数1λ为输入, 输出系统公开参数pp.pp 通常包含系统中所有用户可共享的信息, 如公钥空间PK、私钥空间SK、明文空间M和密文空间C的描述.1系统公开参数的内容并没有严格规定, 在一些例子中可能退化为⊥: 如对于RSA 公钥加密方案, 明文空间和密文空间均与公钥相关, 所以由算法KeyGen 输出.该算法由可信第三方运行, 生成的pp 将作为以下所有算法的输入.当上下文明确时, 常常为了行文简洁省去pp.

• KeyGen(pp): 密钥生成算法以系统公开参数pp 为输入, 输出公/私钥对(pk,sk), 其中公钥公开,私钥由用户秘密保存.

• Encrypt(pk,m;r): 加密算法以公钥pk∈PK、明文m ∈M和随机数r为输入, 输出密文c ∈C.

• Decrypt(sk,c): 解密算法以私钥sk∈SK 和密文c ∈C为输入, 输出明文m′∈M或者⊥表示密文非法.解密算法通常为确定性算法.

正确性.该性质刻画公钥加密的功能性, 确保使用私钥可以正确恢复出对应公钥加密的密文.正式地,对于任意明文m ∈M, 有:

公式(1)的概率建立在Setup(1λ)→pp、KeyGen(pp)→(pk,sk) 和Encrypt(pk,m)→c的随机带上.如果上述概率严格等于1, 则称公钥加密方案满足完美正确性.基于数论假设的公钥加密方案通常满足完美正确性, 而格基方案由于底层困难问题的误差属性, 解密算法往往存在误差.

安全性.令A=(A1,A2) 是攻击公钥加密方案安全性的敌手, 定义其优势函数如下:

在上述定义中,A= (A1,A2) 表示敌手A可划分为两个阶段, 划分界线是接收到挑战密文c∗的时候,state 表示A1向A2传递的信息, 记录部分攻击进展.Odecrypt(·) 表示解密谕言机, 其在接收到密文c的询问后输出Decrypt(sk,c).如果任意PPT 敌手在阶段1 和阶段2 均可自适应访问Odecrypt(·) 的情形下仍仅具有可忽略优势, 则称公钥加密方案满足选择密文攻击下的不可区分(indistinguishability against chosen-ciphertext attack, IND-CCA) 安全, 或者也可称为IND-CCA2 安全; 如果任意PPT 敌手仅在阶段1 可自适应访问Odecrypt(·) 的情形下具有可忽略优势, 则称公钥加密方案满足IND-CCA1 安全.如果任意不可访问Odecrypt(·) 的PPT 敌手A在上述游戏中的优势函数均为可忽略函数, 则称公钥加密方案满足选择明文攻击下的不可区分(indistinguishability against chosen-plaintext attack, IND-CPA) 安全.

3 公钥密码学发展的两条主线

在1976 年Diffie 和Hellman 的开创性论文[4]后, 公钥密码学的发展一日千里、日新月异, 热潮持续至今, 孕育了很多新的密码原语和重要技术.

公钥密码的发展大体有两条主线: 一条是安全性的增强, 从最初的直觉安全演进到可证明的语义安全,再到不可区分选择密文安全和各类超越传统安全模型的高级安全性, 如选择打开攻击安全、抗泄漏安全、抗篡改安全和消息依赖密钥安全; 另一条是功能性的丰富, 从最初简单的一对一加解密到可委派身份密钥的身份加密, 再到支持细粒度访问控制的属性加密乃至极致泛化的函数加密和可对密文进行计算的(全)同态加密.本文将按照这两条主线(如图2 所示) 梳理公钥密码学的发展历程, 介绍重要的成果.

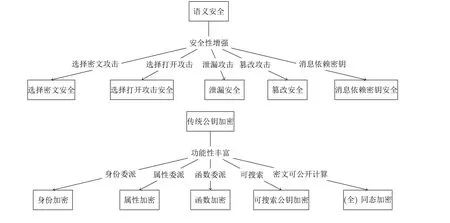
图2 公钥加密发展主线Figure 2 Development of public-key encryption

4 安全性增强

本文在综述安全性增强这条发展主线时, 如果不特意提及, 则约定密码方案为标准的公钥加密方案(定义1).

4.1 传统安全模型

对于密码方案, 给出恰当的安全性定义至关重要, 安全性在必须可达的同时又须足够强以刻画现实中存在的攻击.

随着应用场景的不断丰富和攻击手段的不断增强, 公钥加密的安全性是从弱到强逐渐提升的, 强安全的公钥加密方案往往基于弱安全的公钥加密方案构造.

1976 年, Diffie 和Hellman[4]首次提出了公钥加密的概念但并没有给出具体方案构造.1978 年,Rivest 等[10]基于数论问题构造出了首个公钥加密方案—RSA 加密.在这一阶段, 公钥加密的安全性仅具备符合直觉的单向性, 即在平均意义下从密文中恢复出明文是计算困难的.到上世纪80 年代, 密码学家们逐渐认识到单向性并不足以满足现实的隐私保护需求.具体来说, 对于单向安全的公钥加密方案, 敌手尽管无法从密文中恢复出明文的全部信息, 但有可能恢复出明文的部分信息.而在应用中, 由于数据来源的多样性和不确定性,明文的每一比特都可能包含关键的机密信息(比如股票交易指令中的“买”或“卖”).

1982 年, Goldwasser 和Micali[5]发展了可证明安全的技术框架: 建立安全模型以准确刻画敌手的攻击行为和攻击效果, 将密码方案的安全性归约到计算困难问题的困难性上.此外, Goldwasser 和Micali还指出单向安全的不足, 提出了公钥加密的合理定义—语义安全(semantic security).语义安全的直观含义是密文不泄漏关于明文额外的有效知识, 因此密文对敌手求解明文没有帮助.严格定义颇为精妙, 定义的形式是基于模拟的, 即掌握密文的敌手的视角可以由一个不掌握密文的PPT 模拟器在计算意义下模拟出来.语义安全性可以看做Shannon 完美安全在计算意义的对应, 然而在论证的时候稍显繁琐笨重.

Goldwasser 等[5,11]给出了另一个等价的定义(等价性证明参见Dodis 和Ruhl 的短文[12]), 即选择明文攻击下的不可区分性(indistinguishability against chosen-plaintext attack, IND-CPA).IND-CPA安全定义的直觉是密文在计算意义下不泄漏明文的任意一比特信息, 即任意两个明文对应的密文分布是计算不可区分的, 其中选择明文攻击刻画了公钥公开特性使得任意敌手均可通过自行加密获得任意明文对应密文这一事实.使用IND-CPA 安全进行安全论证相比语义安全要便捷很多, 因此被广为采用.

选择密文安全.IND-CPA 安全仅考虑被动敌手, 即敌手只窃听信道上的密文.1990 年, Naor 和Yung[13]指出敌手有能力发起一系列主动攻击, 比如重放密文、修改密文等, 进而提出选择密文攻击(chosen-ciphertext attack, CCA) 刻画这一系列主动攻击行为, 允许敌手自适应地获取指定密文对应的明文; 所对应的安全性称为选择密文攻击下的不可区分性(indistinguishability against chosen-ciphertext attack, IND-CCA), 即IND-CCA 安全.Naor 和Yung 考虑了两种选择密文攻击, 一种是弱化版本, 称为午餐时间攻击(lunch-time attack), 含义是敌手只能在极短的时间窗口(收到挑战密文之前) 进行选择密文攻击, 该攻击类型对应IND-CCA1 安全; 另一种是标准版本, 敌手可在长时间窗口(收到挑战密文前后)进行选择密文攻击, 该攻击类型对应IND-CCA2 安全, 或简称为IND-CCA 安全.

1998 年, Bleichenbacher[14]展示了针对PKCS#1 标准中公钥加密方案的有效选择密文攻击, 从而实证了关于IND-CCA 安全的研究并非杞人忧天, 而是具有重要的实际意义.从此, IND-CCA 安全成为了公钥加密方案的事实标准.根据模型划分, 构造IND-CCA 安全的公钥加密方案有以下主流的方法技术:

• 随机谕言机模型下:

– OAEP (optimal asymmetric encryption padding) 转换.Bellare 等[15]提出了随机谕言机模型(random oracle, RO), 而后在文献[16] 提出了一种基于陷门置换构造IND-CCA 安全PKE方案的通用转换, 即OAEP 转换.Shoup[17]指出OAEP 转换并不是对所有的陷门置换成立.Fujisaki 等[18]则进一步指出了OAEP 转换应该满足的条件, 并提出了基于RSA 类型陷门置换的RSA-OAEP 方案.

– Fujisaki-Okamoto (FO) 类提升安全性的通用转换.Fujisaki 和Okamoto[19]首先提出了在RO 模型下利用混合加密将IND-CPA 安全的PKE 方案提升为IND-CCA 安全的PKE 方案的通用转换, 其核心思想是引入哈希函数绑定密文的各部分使得密文不可延展.Fujisaki 和Okamoto 在同年[20]将底层PKE 方案的安全性从IND-CPA 安全弱化为单向安全, 这一通用转换称为FO 转换[20,21].类似的通用转换还有许多, 但其核心思想均与FO 转换相似, 如Pointcheval[22]在RO 模型下将单向陷门函数转换为IND-CCA 安全的PKE 方案, 又如Okamoto 和Pointcheval[23]提出的REACT 通用转换.

– FO 类通用转换的改进.由于FO 转换思想简洁、转换高效, 近期的工作主要是在FO 转换的基础上进行改进.Hofheinz 等[24]将FO 转换分为去随机化重加密和哈希映射两个部分进行模式化分析, 将类似于FO 转换的通用转换, 例如REACT[23]、GEM[25]等统一在一起, 阐明了底层PKE 方案的性质、密文结构的不同对FO 转换后得到的PKE 方案安全性的影响, 并推广FO 转换到量子RO 模型下.后续的工作则集中在提升文献[24] 中的归约效率[26]或者降低密文开销[27,28].

• 标准模型下:

– 使用非交互零知识证明将任意IND-CPA 安全的PKE 强化为IND-CCA 安全.Naor 和Yung[13]首次提出双密钥加密策略结合非交互零知识证明(non-interactive zero-knowledge proof, NIZK) 将任意IND-CPA 安全的PKE 方案转换为IND-CCA1 安全; Dolev 等[29]设计出矩阵式加密结构, 结合一次性不可伪造签名(one-time signature, OTS) 和NIZK 将任意IND-CPA 安全的PKE 方案提升至IND-CCA 安全; 受上述两个工作启发, Sahai[30]展示如何用OTS 将普通NIZK 强化为模拟稳固(simulation soundness, SS) 的NIZK, 以此为工具应用Naor-Yung 双重加密范式, 将任意IND-CPA 安全的PKE 方案强化为IND-CCA 安全.Biagioni 等[31]和Cramer 等[32]分别给出了Naor-Yung 双重加密范式的两个变体, 前者对加密随机数进行了安全的重用, 后者使用了新的加密重复策略和消息一致性证明方法.

– 基于弱化的非交互式零知识证明构造IND-CCA 安全的PKE.Cramer 和Shoup[33]提出了一种特殊的指定验证者非交互式零知识证明(designated-verifier NIZK, DV-NIZK)—哈希证明系统(hash proof system, HPS), 并基于HPS 给出了一类基于判定性困难问题的IND-CCA安全的PKE 方案的通用构造.Wee[34]提出了一种特殊的指定验证者非交互式零知识的知识证明—可提取哈希证明系统(extractable HPS, EHPS), 并基于EHPS 给出了一类基于搜索性困难问题的IND-CCA 安全的PKE 方案的通用构造, 该构造不仅解释了已有的方案[35–37], 还启发了基于CDH 假设的新PKE 方案的设计.

– 以结构更丰富的加密方案为起点构造IND-CCA 安全的PKE.Boneh 等[38]以身份加密(identity-based encryption, IBE) 为底层方案, 结合OTS 或消息验证码(message authentication code, MAC) 构造出IND-CCA 安全的PKE 方案.Kiltz[39]将IBE 弱化为基于标签的加密(tag-based encryption, TBE), 结合OTS 构造出IND-CCA 安全的PKE 方案.

– 基于更强的单向陷门函数.Kiltz 等[40]提出了自适应单向陷门函数(adaptive trapdoor functions, ATDF), 并基于此给出了IND-CCA 安全的PKE 方案的通用构造.该构造简洁优雅, 并且涵盖了基于有损陷门函数[41]和相关积单向函数[42]的构造.最近的突破性结果是Hohenberger 等[43]展示了如何仅基于单射陷门函数构造IND-CCA 安全的PKE.

– 基于不可区分混淆的编译器.Sahai 和Waters[44]引入可穿孔伪随机函数, 借助不可区分混淆(indistinguishability obfuscation,iO) 构造出IND-CCA 安全的PKE 方案.该构造实现了Diffie 和Hellman 自20 世纪70 年代起的愿景, 展示了如何将对称加密编译为公钥加密.

– Chen 等[45]提出了可公开求值伪随机函数, 并基于此给出了PKE 方案的通用构造.该构造不仅从更抽象的层次阐释了经典的GM 加密方案[5]和ElGamal 加密方案[46]的设计思想, 还统一了基于(可提取) 哈希证明系统、单向陷门函数、可穿孔伪随机函数与iO的构造.

选择打开安全.IND-CPA 安全模型和IND-CCA 安全模型主要考虑一对一的两方通信场景, 但是PKE 方案常常被应用到多对多的分布式协议当中.例如考虑如下场景,n −1 个发送者用某用户的公钥对某轮协议中(相关联) 的消息进行加密, 并发送给该用户.此时存在一个强力的敌手, 其腐化了该轮协议一部分消息发送方的计算机, 不仅获得了他们密文对应的明文, 还获得了加密用的随机数.类似于两方通信下PKE 方案的语义安全, 在多方的环境下, 仍然希望敌手不会获得除了条件分布以外关于未腐化用户的明文的有效知识.Bellare 等[47]首先考虑了上述的情景, 将这样的安全性称为选择打开(selective opening, SO) 安全, 并从模拟和不可区分两个角度分别给出了SO 安全的SIM-SO 和IND-SO 两种形式化定义.同时, 他们也提出了有损加密(lossy encryption) 这一新概念.简单来说, 有损加密有两种加密模式, 单射模式下利用私钥可以解密密文得到明文, 而有损模式下则是多个密文对应到一个明文, 从而无法正确解密, 他们证明了有损加密方案本身为IND-SO-CPA 安全的, 而具有某种高效打开算法的有损加密方案本身为SIM-SO-CPA 安全的.但是上述的场景—多用户根据同一个公钥加密消息发送给某一用户(敌手腐化发送方取得明文与加密随机数) 与真实的多方协议相去甚远.因此, Bellare 等[48]提出了一个新的场景—某一用户根据多个用户不同的公钥加密发送不同的加密消息给不同的用户(敌手腐化接收方取得私钥).为了区分, 他们称第一种场景下的安全性为发送者SO (sender SO, SSO) 安全, 第二种场景下的安全性为接受者SO (receiver SO, RSO) 安全.SO 安全的主要研究工作集中在如何构造SSO 安全和RSO 安全的PKE 方案上.

• SSO 安全的PKE 的构造: Bellare 等[47]利用有损加密给出了SSO 安全的PKE 方案的构造, 后续一系列研究延续Bellare 等的路线, 围绕着有损加密方案的构造展开.Hemenway 等[49]从多种密码原语出发(例如同态加密、哈希证明系统等) 给出了有损加密的多种构造方法, 结合All-But-N有损陷门函数进一步构造出了IND-SSO-CCA 安全的PKE 方案.Hofheinz[50]将All-But-N有损陷门函数拓展为All-But-Many 有损陷门函数, 构造出了SIM-SSO-CCA 安全的PKE 方案.Fehr 等[51]则采取了另外一条有别于Bellare 的路径.他们先证明了发送者模糊性(sender equivocable, NC) CCA 安全蕴含了SIM-SSO-CCA 安全, 然后给出一种基于哈希证明系统和交叉验证码构造NC-CCA 安全的PKE 方案的通用方法, 进而构造出SIM-SSO-CCA 安全的PKE方案.Huang 等[52]指出了Fehr 等[51]的证明中的问题, 并给出了一个可行的修正方法—将交叉验证码的性质加强.格上SSO 安全的PKE 方案的构造主要是从All-But-Many 有损陷门函数[53,54] 出发.

• RSO 安全的PKE 的构造: Hazay 等[55]首先利用接受者非承诺加密(non-committing encryption for receiver, NCER) 构造了SIM-RSO-CPA 安全的PKE 方案, 并用NCER 的变体构造了INDRSO-CPA 的PKE 方案.Jia 等[56]基于Naor-Yung 双重加密范式给出了IND-RSO-CCA 安全的PKE 的通用构造.该构造将IND-RSO-CPA 安全的PKE 方案和CCA 安全的PKE 方案相结合, 并通过NIZK 转换为IND-RSO-CCA 安全的PKE 方案.Hara 等[57]将类似的方法推广到了SIM-RSO-CCA 安全的PKE 方案的构造中, 并额外基于DDH 假设给出了一个效率较高的具体构造.

孤立的SSO 安全或者是RSO 安全仍然与现实多对多分布式协议的安全性要求并不十分吻合, 后续有些研究开始考虑更为广泛意义下的SO 安全性.例如, Lai 等[58]首次在一个模型下同时考虑SSO 和RSO 两种安全性, 形式化提出了基于模拟的SIM-(w)Bi-SO-CCA 安全性, 并基于密钥模糊性哈希证明系统这一新的密码原语给出了SIM-wBi-SO-CCA 安全的PKE 方案的通用构造.这些研究成果使得SO 安全的PKE 方案可以有效保障多对多分布式协议的安全.

另外, 除了关于SO 安全的PKE 方案具体构造的研究外, SO 安全性与其他安全性间的强弱联系等理论问题也得到了深入的研究.例如, Bellare 等[47,59]证明了SIM-SSO-CPA 安全性在黑盒意义上蕴涵IND-SSO-CPA 安全性; Bellare 等[48]证明了标准的IND-CPA 安全性不蕴涵SIM-SSO-CPA 安全性等.

消息依赖安全.IND-CPA 安全模型下敌手可以获得消息对应的密文, 而IND-CCA 安全模型下敌手还可以额外获得选定密文对应的明文, 除此之外, 敌手不能获得其他与sk 有关的信息, 这通常无法契合复杂的现实应用场景.以Windows 操作系统下最为知名的文件加密程序BitLocker[60]为例, 其不仅将保密文件经过加密放在硬盘上, 还将相应的密钥对加密存储在硬盘上, 那么对于恶意的敌手而言, 他不仅获得了机密文件对应的密文, 还获得了私钥的密文, 此类攻击行为显然无法被IND-CPA 安全和CCA 安全所刻画, 类似的场景还有匿名证书系统[61]等.为了刻画敌手可以获得加密的私钥的能力, Black 等[62]首先定义了消息依赖密钥(key-dependent message, KDM) 安全, 其含义简单来说就是, 即使敌手看到了与密钥相关的密文, 密码系统仍然可以保证通信的机密性.非正式地说, 假定n组密钥对为{(ski,pki)}i∈[n],F为密钥相关函数集, 如果PKE 方案的敌手在看到f(sk1,sk2,···,skn)(任何一个f ∈F下) 在所有pki下加密的密文后, 其他消息的机密性对于敌手而言仍然保持, 那么就称该PKE 方案为F-KDM 安全的.显然, 密钥函数集F越大, 对应的F-KDM 安全性越强, 而关于消息依赖密钥安全研究的一个核心问题就在于如何扩大密钥函数集F.

Boneh 等[60]基于DDH 假设构造出首个KDM-CPA 安全的PKE 方案, 其支持的密钥相关函数集为仿射函数Faff.Applebaum 等[63]基于LWE 假设构造出另一个Faff-KDM-CPA 安全的PKE 方案.之后, Malkin 等[64]基于DCR 假设给出了一个相关密钥函数集为次数有界多项式Fpoly的KDM-CPA安全的PKE 方案.Wee[65]基于同态的哈希证明系统给出了一个通用的KDM-CPA 安全的PKE 方案设计框架, 统一了诸多已有的具体构造[60,66].

后续工作致力于构造更强的KDM-CCA 安全的PKE 方案.Camenisch 等[67]指出Naor-Yung 双重加密范式可将F-KDM-CPA 安全的PKE 方案强化为F-KDM-CCA 安全的PKE 方案.然而该通用方法的效率不高, 需要使用NIZK, 且密文尺寸为O(λ) 数量级.之后, Hofheinz[68]针对KDM 安全的一个特例—循环安全(circular security), 基于DCR、DDH 和DLIN 假设构造了密文紧致(尺寸为O(1))的PKE 方案, 但是密文仍然包含50 个以上的群元素.Han 等[69]延续文献[70] 的技术框架, 提出了一个密文紧致的Faff-KDM-CCA 安全的PKE 方案, 并进一步拓展为Fpoly-KDM-CCA 安全的PKE 方案.Kitagawa 等[71]基于DDH 假设构造出了F-KDM-CCA 安全的PKE 方案, 密文尺寸为O(λ) 数量级.Kitagawa 等[72]提出对称密钥封装这一新型密码原语改进之前的方案, 得到了更为高效Faff-KDM-CCA安全的PKE 方案, 密文相较于Han 等[69]的Faff-KDM-CCA 安全的PKE 方案进一步减少了10 个以上的群元素, 而其Fpoly-KDM-CCA 安全的PKE 方案的密文长度相较于Han 等[69]的Fpoly-KDM-CCA安全的PKE 方案实现了数量级上的缩减, 当多项式次数的上界为d, 密文长度为O(d), 而Han 等[69]方案的密文长度为O(d9).

类似于SO 安全的研究,对KDM 安全的研究除了关于KDM 安全的PKE 方案的具体构造,KDM 安全性与其他安全性间的强弱联系等理论问题也得到了深入的研究.例如, Kitagawa 等[73]证明了KDMCPA 安全和KDM-CCA 安全在黑盒意义上是等价的; Waters 等[74]证明了对于PKE 方案而言, 单密钥循环安全在黑盒意义上蕴含了支持相关函数集为任意有限深度电路的KDM 安全等.

4.2 超越传统安全模型

IND-CPA 与IND-CCA 仍然属于传统安全模型范畴.传统安全模型的一个基本假设是完美黑盒, 即密码算法的软硬件实现可以完美防护内部秘密信息(如私钥、随机数), 敌手仅能以黑盒的方式通过预定义的接口收集信息以分析密码算法, 而无法篡改或通过其他方式获取内部秘密信息.

完美黑盒假设可以细分为抗泄漏、抗篡改假设:

• 抗泄漏: 敌手无法通过预定义接口以外的信道获取秘密信息.

• 抗篡改: 敌手无法篡改密码算法软硬件实现及其中的秘密信息.

长久以来, 传统安全模型的“完美黑盒” 假设被认为是合理稳固的.然而, 自上世纪90 年代起, 密码分析技术的飞速发展表明密码算法的软硬件实现难以达到真正的黑盒, 上述两大假设均不成立.攻击者既可以通过分析算法运行时间[75]、监测能耗水平[76]、分析电磁辐射[77]、冷启动读取内存[78]等多种侧信道攻击获取安全模型既定接口之外的秘密信息, 也可以通过故障植入[79,80]、截断线路、加热冷冻、射线照射等多种手段对密码算法的软硬件实现及其中的秘密信息实施篡改.这些低成本的有效攻击导致许多在传统安全模型中可证明安全的密码方案在实际应用中并不安全.为了防御上述攻击, 工业界一般采用屏蔽、混淆等硬件层次的防御方法, 但大多只针对具体攻击和具体方案有效, 通用性不足, 难以应付层出不穷的泄漏、篡改攻击.密码学界从2004 年起致力于从源头上给出抗侧信道攻击的通用解决方法, 即在经典安全模型的基础上建立泄漏安全模型以刻画绝大多数已知甚至未知的侧信道攻击(刻画方式通常是将攻击者通过侧信道可能获得的秘密状态信息表达为关于秘密状态的多项式可计算的函数), 奠定了获得可证明抗侧信道攻击的理论基础.

抗泄漏安全.2004 年, Micali 和Reyzin[81]提出了物理可观测安全密码学, 拉开了从理论上防御泄漏攻击的研究序幕.2008 年, Dziembowski 和Pietrzak[82]正式提出了抗泄漏密码学, 在传统安全模型之上, 通过允许敌手访问泄漏函数建立了更强的泄漏安全模型.在泄漏安全模型下可证明安全的密码方案能够抵御一系列已知或未知的侧信道攻击, 适用于各种复杂未知的应用环境.

总体而言, 泄漏模型通过增加泄漏谕言机Oleak(·) 强化传统安全模型.敌手可以自适应地向泄漏谕言机发起一系列泄漏询问fi: sk0,1}ℓi并获得相应的结果, 其中fi是关于私钥的函数, 称为泄漏函数.不同的泄漏模型通过对泄漏函数施加不同的限制获得.Micali 和Reyzin[81]首先给出唯计算泄漏模型, 即要求泄漏函数的输入只能是私钥参与计算的部分.然而冷启动攻击表明该模型无法全面刻画现实攻击, 未参与计算的存储单元同样可能发生泄漏.之后出现的模型对发生泄漏的存储单元不再加以限制, 即所有的存储单元均可能存在泄漏.其又可进一步分为相对泄漏模型(relative memory leakage model) 和连续泄漏模型(continual memory leakage model), 前者对密码系统在整个生命周期内的泄漏量存在一定限制;后者考虑密码系统可进行连续更新, 只对状态更新之间的泄漏量存在一定限制, 而对整个生命周期内的泄漏量没有限制.

• 相对泄漏模型中, 攻击者能够通过访问泄漏函数获取关于私钥的信息.对泄漏函数施加的细粒度限制进一步细分了此类模型.Akavia 等[83]提出的有界泄漏模型(bounded leakage model) 的限制是其中ℓi为敌手自适应选择的泄漏询问fi的输出长度,ℓ为泄漏量上界, 泄漏率被定义为比值ℓ/|sk|, 用于衡量泄漏量的多少.Akavia 等在有界泄漏模型下基于LWE 假设给出了抗泄漏安全的公钥加密方案和身份加密方案.随后Naor 和Segev[84]基于哈希证明系统给出了有界泄漏模型下抗泄漏公钥加密的通用构造, 并给出多个实例化方案, 特别地, 基于Cramer-Shoup加密方案的变体给出了泄漏率为1/6−o(1) 的选择密文安全构造.此外, Naor 和Segev[84]还将有界泄漏模型放宽为噪声泄漏模型(noisy leakage model), 该模型不再对泄漏函数输出长度总和进行限制, 仅要求泄漏后私钥的最小熵仍大于预设的下界.后续的工作致力于提升抗泄漏选择密文安全公钥加密方案的泄漏率.Liu 等[85]基于Cramer-Shoup 加密方案的新变体给出了泄漏率为1/4−o(1) 的构造.Dodis 等[86]猜测完全基于哈希证明系统的选择密文安全构造泄漏率不可能大于1/2−o(1).Qin 等[87]等结合哈希证明系统和一次性有损过滤器(one-time lossy filter)给出了选择密文安全公钥加密的新构造, 并在文献[88] 中通过精心的实例化达到了最优泄漏率1−o(1).Chen 等[89]对有损陷门函数[41]进行弱化, 提出正则有损函数(regular lossy function, RLF), 并展示了其在抗泄漏领域的强力应用: 一方面正则有损函数蕴含了最优泄漏率的单向函数和消息验证码, 另一方面与哈希证明系统结合则可构造出具有最优泄漏率的选择密文公钥加密方案.由于代数友好的哈希证明系统蕴含正则有损函数, 因此该结果否证了Dodis 等人[86]的猜想.Chen等[90]综合不可区分混淆(iO)、可穿孔(公开求值) 伪随机函数和有损函数给出了构造抗泄漏公钥加密的非黑盒新路线, 方法的核心是利用iO将可穿孔(公开求值) 伪随机函数编译为抗泄漏版本, 并借助有损函数达到最优泄漏率.

有界泄漏模型和噪声泄漏模型的泄漏容忍上界正比于私钥长度, 泄漏上界的提升将导致密码系统私钥长度的增加和运行效率的下降.为了在泄漏上界极大(如O(2λ)) 的情况下尽可能实现优良的运行效率, Alwen 等[91]提出有界获取模型(bounded retrieval model).该模型允许敌手获取关于私钥高达ℓ=O(2λ) 比特量级的信息, 同时要求密码算法运行时间与泄漏量ℓ无关, 仍为关于安全参数λ的多项式.Alwen 等[92]利用身份哈希证明系统基于不同困难假设构造了一系列有界获取模型下抗泄漏的身份加密方案.Dodis 等[93,94]观察到上述相对泄漏模型的共同点是要求泄漏后私钥仍有一定的统计意义下的最小熵.于是, 他们将统计意义进一步放宽到计算意义, 得到了更具一般性的辅助输入模型, 并在该模型下构造了抗泄漏的公钥加密方案.

• 持续泄漏模型: 该类模型中针对密钥具有连续更新机制的密码系统定义.攻击者每个更新周期内都可以获得任意内存单元的泄漏.在该模型下, Brakerski 等[95]利用线性代数的技巧, 基于双线性群中的线性假设构造出抗泄漏的PKE 方案和IBE 方案.Lewko 等[96]利用双系统加密技术,给出了更强意义下的抗泄漏的(H)IBE 方案和属性加密方案, 其中泄漏不仅可以针对一个身份/属性的多个私钥发生, 还可针对主私钥发生.Lewko 等[97]基于合数阶群中的判定性假设, 给出抗泄漏的公钥加密方案, 且允许更新过程中的泄漏量超过指数级别.Yuen 等[98]将连续内存泄漏模型和辅助输入模型结合, 利用双系统加密技术给出了抗泄漏的(H)IBE 方案.以上持续泄漏模型的局限是仅允许泄漏发生在每个私钥生命周期中, 不允许在私钥更新过程中发生泄漏.Dachman-Soled等[99]利用不可区分混淆构造了一个编译器, 可对持续泄漏模型下的公钥加密方案进行强化, 进一步容忍私钥更新过程中的泄漏.

主流的泄漏安全模型聚焦私钥的泄漏, 但是, 在真实的泄漏场景中, 不仅仅是存储私钥的存储单元可能存在泄漏, 参与计算的存储单元甚至所有的存储单元都可能存在泄漏.那么在一定的程度上来说, 只考虑私钥的泄漏是不合理的, 更强的抗泄漏模型还应考虑密码算法执行中各类存储单元的泄漏, 例如使用的随机数的泄漏.针对广泛情形下的泄漏, 一条可行的技术路线是研究抗泄漏的存储编码技术, 抗泄漏的存储编码技术保证敌手即使获得了部分消息编码后的信息, 仍然无法获得原始消息的有效知识.如此, 如果算法本身将随机数进行抗泄漏编码后存储, 则可以满足抗随机数泄漏的性质.但正如Goldwasser 和Rothblum[100]指出的, 安全模型不进一步限制敌手行为, 则难以抵御任意存储单元的泄漏攻击, 故存储编码方案的构造通常还需要其他对敌手限制的假设.Davì 等[101]提出了抗泄漏存储的存储编码技术, 其在存储泄漏相互独立的假设和泄漏函数低复杂度的假设要求下, 利用双源提取器等技术得到了两种抗泄漏存储编码方案.Dziembowski 等[102]仍基于存储泄漏相互独立等假设, 推广[101] 到持续泄漏模型下, 可容忍更高程度的泄漏, 但也需要动态地存储更新的过程.Dodis 等[103]则进一步基于文献[97] 中的技术去除了存储更新过程中对不同存储间同步通信的要求, 使得存储编码方案更加方便快捷, 契合现实使用要求.除了上述的存储编码技术外, 另外一条技术路线是研究抗不同类型泄漏的通用编译器, 它们能将非抗泄漏的密码方案转换为抗泄漏的密码方案.在不同类型的泄漏下, 抗泄漏的通用编译器也得到了充分的研究[100,104,105].

抗篡改安全.同在2004 年, Gennaro 等[106]提出了抗篡改密码学, 在传统安全模型之上, 通过允许敌手访问篡改函数获取秘密状态的额外信息.例如, 具体到公钥加密, 敌手可以询问解密谕言机(ϕ,c) 以获得c在密钥ϕ(sk) 下的解密值.可见, 区别于泄漏攻击敌手的被动性, 篡改攻击的敌手具有主动性.因此, 篡改攻击的威力极强, Boneh 等[107]曾指出, 一个随机性的错误足够攻击基于RSA 的签名, 从而, 研究抗篡改安全的公钥密码是非常重要的.

就最广泛的意义而言, 拥有篡改能力的敌手可以同时篡改算法对应的电路C和内部秘密状态st (例如包含私钥sk), 具体来说, 敌手可以对(C,st) 实施任何的篡改函数得到(C′,st′) =f(C,st), 这被称为计算篡改(tampering with computation) 模型.若不具有篡改能力的敌手能访问某个密码算法谕言机C(st,·),那么具有篡改能力的敌手就能访问篡改后的密码算法谕言机C′(st′,·).显然, 如果不给f施加限制, 那么可使篡改后的密码算法对应的电路C′直接输出内部状态st, 而内部状态st 往往包含sk, 从而敌手可直接从密码算法谕言机中获得sk 从而实现任意的解密.为了避免类似的平凡攻击, 在讨论抗篡改安全模型时,通常均会限制f从某个篡改函数集Φ 中选择.篡改安全模型的强弱取决于篡改函数集Φ 的大小, 因此如何扩大可容忍的篡改函数集是抗篡改密码学的核心问题.Ishai 等[108]在计算篡改模型下研究了这个问题, 他们采取的方法是构造通用的电路编译器, 将不抗篡改攻击的密码电路编译为具有篡改性质的.但是,他们只能在非常受限的篡改函数集Φ 上得到一般的通用电路编译器.后续一系列研究[109–111]致力于扩展文献[108] 中篡改函数集的限制, 但是效果比较有限, 与实际可行的篡改函数集相比仍存在较大差距.

与最广泛的计算篡改模型相比, 目前在唯内存篡改(memory-only tampering) 模型取得的进展更多.在唯内存篡改的模型下, 敌手只能对内部秘密状态st 进行篡改, 而不能对电路本身进行篡改.内部秘密状态主要可分为密钥sk 和随机数, 但是文献[112] 指出即使篡改少量的随机数, 对整个密码系统的影响都是毁灭性的, 故目前关于抗唯内存篡改的研究通常假设篡改攻击的敌手仅能篡改私钥sk, 即实施相关密钥攻击(related-key attack, RKA).具体地, 如果密码算法可以抗篡改函数集为Φ 的篡改攻击, 则称该密码算法为Φ-RKA 安全.而关于RKA 安全的密码方案的研究主要可分为三类, 一类研究的着重点在于构造具体的方案, 而另外一类研究的着重点则在于构造通用的强化方法, 此外, 亦有一些关于不可能结果的理论研究.

• 具体方案: Bellare 等[113]首次提出了针对密码算法的RKA 安全的理论模型, 并展开了对PRF、PRP 的RKA 安全的研究.早期RKA 安全的研究主要集中在PRF、PRP 这类的密码原语上[114–116].Bellare 等[115]首次将RKA 安全的理论模型推广到PKE 和IBE 上, 并且证明了可利用BCHK 转换[38]将Φ-RKA 安全的IBE 转换为Φ-RKA 安全的PKE.Wee[117]基于适应性陷门关系给出了RKA-CCA 的通用构造, 并分别基于BDDH、LWE 等假设得到了相应的实例化, 但是Wee 的构造篡改函数集Φ 限制在仿射函数集Φaff.Bellare 等[118]则延续文献[115] 的研究方法, 从RKA 安全的IBE 入手, 基于非标准d-EDBDH 假设给出了篡改函数集为d次多项式Φpoly的IBE 方案, 从而得到了Φpoly-RKA-CCA 安全的PKE 方案.为了基于标准假设构造RKA-CCA 安全的PKE 方案, Qin 等[119]将文献[120] 中提出的不可延展密钥导出函数(nonmalleable key derivation functions, NM-KDF) 扩展为连续不可延展密钥导出函数(cNM-KDF),并以此为工具将一系列密码方案(包括公钥加密) 提升为对函数集Φhoeiocr(高输出熵且输入-输出抗碰撞的函数集, 该函数集包含次数有上界的多项式函数) 的Φhoeiocr-RKA 安全的方案.Chen 等[121]首次提出不可延展函数(non-malleable function, NMF) 的概念, 建立起其与单向函数之间的全面联系, 并展示了NMF 在抗篡改安全领域中的强力应用, 具体地, 将cNM-KDF 强化为RKA 安全的可认证密钥导出函数, 并基于NMF 给出简洁的黑盒构造.该构造凝练了Qin 等cNM-KDF 的本质思想, 并且扩大了可容许的篡改函数集, 从而提高了提升转换的编译效果.Fujisaki 等[122]则基于DBDH 假设进一步将篡改函数集推广到ΦaInv(有效可逆函数构成的函数集).为了得到更为广泛的篡改函数集, 同时绕过Gennaro 等[106]给出的不可能结果—针对sk 无限制的篡改函数集实现RKA 安全是不可能的, Damgård 等[123]提出了有界篡改模型.有界篡改模型虽然不限制篡改函数集,但是限制敌手的篡改次数,衡量其安全强度的一个重要指标是篡改率ρ(λ):=τ(λ)/s(λ)(其中τ(λ) 为篡改的次数上界,s(λ) 为sk 的比特长度).Damgård 等[123]基于双线性映射得到了第一个ρ(λ)=O(1/λ) 的RKA 安全的PKE 方案.Faonio 等[124]基于哈希证明系统得到了不基于双线性映射的ρ(λ)=O(1/λ) 的RKA 安全的PKE 方案.

• 通用的强化方法: 与具体方案不同, 这条路线主要考虑如何采用通用的方式将不具有RKA 安全性的密码方案转换为具有RKA 安全性的密码方案, 而这也正是Gennaro 等[106]最初构造RKA 安全密码方案的主要着手点.Dziembowski 等[125]提出了不可延展编码(non-malleable code) 这一新的密码原语, 并基于该原语构造了一个能将不具有RKA 安全的密码方案编译为具有RKA 安全的密码方案的通用编译器, 但是他们只证明了该编码的存在性, 而没有给出在较强安全模型下该编码的构造.后续的工作主要围绕不可延展编码的构造展开, 而其核心问题仍然是如何扩大篡改函数集的大小, 例如Faust 等[126]考虑了空间有界的篡改函数集, Brian 等[127]考虑了多项式深度电路对应的篡改函数集等.

• 不可能结果: Wang 等[128]证明了在有界篡改模型下, 即使敌手的篡改次数被限制为一次, 也无法通过黑盒归约基于任意的计算困难问题证明多种具有唯一性的密码原语的RKA 安全性.具体包括: 可验证随机函数、单射单向函数、具有唯一性的签名和具有唯一消息性的加密, 涵盖了Cramer-Shoup 加密[33]、RSA 签名[10]、Waters 签名[129]等方案.

4.3 紧归约安全

密码学中的紧归约安全研究始于伪随机函数[130].具体来说, 假定安全性证明中包含归约R, 其将高效的敌手A转换为归约算法RA解决底层某个计算困难问题,记敌手A和归约算法RA的运行时间分别为tA(λ)和tRA(λ), 优势分别为ϵA(λ)和ϵRA(λ), 且有tRA(λ)/ϵRA(λ)=ℓ(λ)·tA(λ)/ϵA(λ), 那么ℓ(λ)即可作为衡量归约损失的度量,ℓ(λ) 越大, 则归约损失越大, 归约越低效.在密码背景下, 归约算法和敌手的运行时间通常均为多项式级别, 因此密码学归约更关注比值L(λ) =ϵA(λ)/ϵRA(λ), 如果L(λ) =O(1)(或者L(λ) =O(λ)), 则称对应的密码方案为(几乎) 紧归约安全的.通常来说, 如果采用一般的混合论证技术(hybrid argument),L(λ) 往往与敌手控制的参数相关, 例如用户的数量n、加密查询的次数Qe、解密查询的次数Qd等.一般来说,n、Qe和Qd的数量级在230以上[131,132], 这对归约效率影响极大.密码方案若安全归约低效, 则需增大安全参数以保证方案的安全性, 进而会影响方案效率, 而具有紧归约安全的密码方案无须调整安全参数.综上, 对密码方案紧归约安全的研究不仅具有理论价值, 也具有实际意义.

公钥密码的紧归约安全的研究发源于文献[133] 中对多挑战多用户模型下归约效率的讨论, 但其并没有得到O(λ) 或者是O(1) 的紧归约CCA 安全的PKE 方案.而后, 密码学家对如何在标准模型下构造多挑战多用户的紧归约CCA 安全的PKE 方案这一问题展开了广泛且深入的研究.总的来说, 目前在多挑战多用户的设定下设计紧归约CCA 安全的PKE 方案主要有两种方式, 第一种基于Naor-Yung 双重加密范式, 第二种基于哈希证明系统.

• 基于Naor-Yung 双重加密范式: 由于Naor-Yung 双重加密范式的转换是紧的, 即在紧归约安全的NIZK 下, 紧归约CPA 安全的PKE 方案可转换为紧归约CCA 安全的PKE 方案, 而且紧归约CPA 安全的PKE 方案很容易构造[133], 所以基于双重加密范式的紧归约的CCA 安全的公钥加密方案主要集中在如何构造紧归约安全的NIZK 上.Hofheinz 和Jager[134]设计了第一个紧归约安全的结构保持的签名方案(structure-preserving signature, SPS), 并利用Groth-Sahai 证明[135]得到了第一个紧归约安全的无界模拟稳固(unbounded simulation sound, USS) 的NIZK,从而得到第一个基于标准假设的紧归约CCA 安全的公钥加密方案.但是该方案开销过大, 后续的工作主要集中在如何保证紧归约的同时使NIZK 更为高效.Abe 等[136]通过构造紧归约安全的带标签的单次签名得到了更为高效的紧归约安全的SPS, 使用文献[134] 中的转换框架得到了高效的紧归约USS 的NIZK; Libert 等[137,138]则更进一步, 他们注意到在Naor-Yung 双重加密范式下, 利用更弱的NIZK 即可得到CCA 安全的PKE 方案, 他们将NIZK 弱化为准适应性NIZK (quasi-adaptive NIZK, QANIZK), 并利用线性同态性结构保持签名(linear homomorphic SPS, LHSPS) 构造了高效的紧归约USS 的QANIZK; Gay 等[139]利用适应性划分(adaptive partition) 技术构造了一个紧归约安全且非常高效的MAC, 并借助Bellare-Goldwasser 转换[140]得到一个非常高效的SPS, 使用文献[134] 中的转换框架也就得到了高效的紧归约USS 的NIZK;目前在标准模型、标准假设下最好结果是Abe 等[141]构造的紧归约USS 的QANIZK 与SPS,其QANIZK 的证明部分只需要14 个群元素的开销且公共参数串的长度与安全参数无关, 其SPS的签名部分只需要11 个群元素的开销且其验证算法只使用7 个配对积方程.

• 基于哈希证明系统: 传统HPS[33,142]的固有结构难以实现紧归约CCA 安全, 故相关工作主要集中在如何设计HPS 的变体, 并基于此来设计紧归约CCA 安全的PKE 方案.Gay 等[143]根据标签的比特位来线性组合多个HPS 的私钥, 并基于标签对挑战密文、解密谕言机询问进行划分, 以O(λ) 的损失引入了指数量级的熵, 得到了第一个不基于双线性映射的紧归约CCA 安全的PKE方案; 但是文献[143] 中由于私钥和公钥的数量与安全参数成线性关系而开销过大, 文献[144] 则进一步改造HPS 为合法证明系统(qualified proof system, QPS), 借助于或证明(OR proof) 的技术将私钥、公钥的数量缩减到常数, 得到了非常高效的紧归约CCA 安全的PKE 方案.后续的工作主要围绕这二者进一步展开, 并将类似技术推广到更强的安全模型下[132,145,146].

除此之外, 还有许多基于未充分研究的假设的紧归约工作, 其主要可以分为基于非标准的q类(qtype) 假设[50], 以及基于合数阶群上的计算困难假设[147,148], 这里不一一阐述, 关于这方面更进一步的介绍请参阅文献[149].

5 功能性丰富

本文在综述功能性丰富这条发展主线时, 如果不特意提及, 则约定将密码方案的安全模型限定为对应功能性下基本的安全模型.

5.1 身份加密

通常, 传统公钥加密的密钥产生算法得到的公钥不具备语义特性, 因此公钥与用户的身份信息必须通过可信第三方签发的证书进行绑定, 在实际应用中, 公钥必须通过PKI 体系的认证才能使用.为了摆脱对PKI 体系的依赖, Shamir[150]提出了身份加密(identity-based encryption, IBE) 这一新概念.相比于传统公钥加密, 身份加密增加了密钥派生算法, 即可以通过主私钥msk 派生出针对身份id 的身份密钥skid.其中, id 允许用户使用任意字符串(如手机号码、Email、地址) 作为公钥.IBE 规避了复杂的证书管理与公钥分发验证过程, 不再依赖PKI.不过, IBE 亦有一些缺点, 例如, IBE 方案的用户私钥由可信的PKG生成, 密钥托管(key escrow) 的问题难以避免.

Shamir 最初的工作只给出了IBE 的概念, 并没有给出具体方案.直到2001 年前后, 三组密码科学家几乎同时独立地给出了IBE 的具体构造, 分别是Sakai 等[151]基于双线性Diffie-Hellman 逆假设、Boneh 等[152]基于判定性双线性Diffie-Hellman(DBDH)假设和Cocks[153]基于二次剩余假设.Gentry等[154]与Horwitz 等[155]提出了层级身份加密(hierarchical IBE, HIBE).以上方案均在随机谕言机模型下可证明安全.为了在标准模型下构造安全的IBE 方案, Canetti 等[156]提出了较弱的选择身份模型(selective-identity model), 即敌手必须在游戏的开始阶段承诺挑战身份id∗, 而非自适应选择.Boneh 和Boyen[157]在选择身份模型下基于DBDH 假设给出了不依赖随机谕言机的IBE 方案.随后, Boneh 和Boyen[158]展示了如何使用可容许哈希函数(admissible hash function) 实例化随机谕言机, 得到标准模型下的IBE 方案, 然而该方案效率低下无法应用于实际.Waters[129]通过巧妙的设计身份到群元素的映射实例化随机谕言机, 基于DBDH 假设得到了首个标准模型下高效的IBE 方案.Hohenberger 等[159]给出了基于不可区分程序混淆和可容许哈希函数实例化全域哈希类范式中随机谕言机的方法, 应用该方法可将Boneh-Franklin IBE[152]的安全性从随机谕言机模型提升到标准模型.上述所有IBE 方案在证明中均采用的是分割策略(partition strategy), 即归约算法将身份空间I切分为I0和I1, 期望敌手选择I0中的身份进行私钥询问, 选择I1中的身份作为挑战.分割策略成功的概率决定了归约的松紧.Katz 和Wang[160]指出当IBE 的私钥生成算法符合全域哈希签名形式时(如Boneh-Franklin IBE), 可以使用双私钥的技术收紧归约.然而这种技术应用范围仅局限于随机谕言机模型下的部分方案, 不适用于标准模型下的IBE 方案.Gentry[161]基于判定性可增双线性Diffie-Hellman 指数(DABDHE) 假设给出了标准模型下紧归约的高效IBE 方案.此外, Gentry 在该工作中还首次为IBE 引入了匿名性.Gentry 的工作是IBE 发展的一个里程碑, 后续的研究方向转向如何基于格基假设设计IBE.

基于格的IBE 与基于双线性映射的IBE 演进路线基本一致.Gentry 等[162]首先构造出对偶的Regev PKE 方案, 再利用随机谕言机将其升级为IBE 方案.Agrawal 等[163]设计了格基采样算法, 以此在选择身份模型下设计出首个不依赖随机谕言机的IBE 方案.Cash 等[164]设计了格基代理算法, 设计出首个完全安全的标准模型下的IBE 方案.虽然文献[164] 达到了适应性安全, 但是由于其格基代理算法的固有结构使得其公钥、私钥、密文长度都是O(λ) 的, 其效率远不及文献[163] 中选择身份模型下安全的公私钥、密文开销仅为O(1) 的IBE 方案, 故后续的工作主要集中在如何兼顾完全的适应性安全以及较高的效率[165–171].其中, Yamada[170]设计了新的划分技术, 给出了兼顾安全性和效率的优良结果, 其公钥长度为O(log2λ), 私钥和密文长度均为O(1) 常数量级.目前为止, 最优的结果由文献[172] 给出, 其进一步改进了Yamada[170]中的划分技术, 在保持安全性和私钥、密文长度开销几乎不变的情况下, 将公钥长度降低到了ω(1) 超常数, 具体的方案下可为O(log logλ).

在IBE 的各种具体构造百花齐放后, 密码学者开始探索构造的不可能结果.Boneh 等[173]指出IBE无法以黑盒的方式由陷门置换或CCA 安全的PKE 构造得出.Papakonstantinou 等[174]指出IBE 无法以黑盒的方式基于DDH 假设构造得出.Döttling 和Garg[175]使用基于混淆电路(garbled circuits) 的非黑盒技术绕过上述不可能结果, 首次基于计算性Diffie-Hellman 假设或大整数分解假设构造出IBE.

在通用构造方面, Döttling 和Garg[176]展示了如何基于任意选择安全的IBE 构造完全安全的IBE.Hofheinz 和Kiltz[177]抽象出离散对数群上的可编程哈希函数(programmable hash function, PHF), 以此解释了一类标准模型下基于分割证明策略的IBE 方案.Zhang 等[171]提出并设计出格基可编程函数,以此为工具设计出高效的IBE 方案.Alwen 等[92]和Chen 等[178]提出了身份哈希证明系统, 阐释了一系列基于判定性假设的IBE 方案的设计思想[161,162,179,180].Chen 等[181]提出了身份可提取哈希证明系统, 阐释了一系列基于搜索性假设的IBE 方案的设计思想[35,182–185].

最近关于IBE 的工作主要是集中在如何增强IBE 的功能性和安全性, 构造IBE 的变体以应对更为丰富的实际场景、更加契合实际使用要求.在功能性上, 一个重要问题是如何使得PKG 拥有类似于PKI的密钥撤销(key revocation) 的功能.事实上, 早在文献[152] 中就提出过一种朴素的撤销思路, 即PKG每隔一定时间段内为诚实用户更新关于(id,t) 的功能密钥, 但是通信开销与用户成正比而显得过于笨重.Boldyreva 等[186]第一次形式化了可撤销IBE (revocable IBE, RIBE) 的安全模型, 利用二叉树构造了通信开销为对数量级的RIBE.Seo 等[187]讨论了文献[186] 中RIBE 安全模型的缺陷并加以修正, 后续关于RIBE 的工作[188–190]的安全模型均基于此修正增强后的安全模型.除了对于密钥撤销这一功能性的考量, IBE 的计算效率、身份匹配模式等性能性、灵活性的主题也都得到了广泛且深入的研究[191–193].

5.2 属性加密

如果把身份加密看作一种访问控制的策略, 那么IBE 只有当解密者拥有加密者所期望的身份才能进行正确解密, 这属于一对一的简单访问控制结构, 但是对于现实应用而言, 通常希望一个加密的文件对于拥有某种权限的人都能解密, 即实现一对多的访问控制结构, 从而IBE 这种简单的访问控制结构是远远不够的, 需要新的密码原语以提供更强大的访问控制结构.Sahai 和Waters[194]拓展了IBE 的内涵, 结合秘密共享方案, 提出第一个基于门限访问控制的属性加密(attribute-based encryption, ABE) 方案, 具体来说, 他们将身份加密下的身份看作由不同的属性构成, 这种ABE 只要解密者的属性密钥与加密者所期望的属性集合足够相似即可以进行正确解密.相比于身份加密下实现的一对一的访问控制结构, ABE 的主要优点是支持更为丰富、强大的控制策略, 具有一对多的访问控制结构, 更加灵活、更加细粒度.

Goyal 等在文献[195] 中正式给出了ABE 的语义, 他们考虑到密文和密钥在控制与被控制关系上的对称性, 将ABE 进一步划分为密钥策略的ABE (key-policy ABE, KP-ABE) 以及密文策略的ABE(ciphertext-policy ABE, CP-ABE) 以适用于不同的应用场景, 顾名思义, KP-ABE 就是将控制策略与委派的属性密钥相绑定, 而将属性集与密文相绑定, 能够正确解密当且仅当密文的属性集符合密钥的控制策略, CP-ABE 亦作类似解释, 除此之外, 他们利用双线性映射、秘密共享, 给出了第一个选择属性模型下的单调访问控制结构(即与门和或门构成的布尔电路) 的KP-ABE 方案, 但需要注意的是, 不同于秘密共享, 他们定义的ABE 还需要额外满足抗合谋性.但是也正是为了满足抗合谋性, CP-ABE 的构造显得较为困难, Bethencourt 等[196]在一般群模型(generic group model, GGM) 下通过给不同的属性密钥引入随机数以防止其重组与合谋实现了第一个支持单调访问控制结构的CP-ABE.利用类似的思想, Cheung和Newport[197]在标准模型下构造了只支持与门构成的访问控制结构的CP-ABE.Waters[198]则开发了新的证明技术, 其通过将线性秘密共享嵌入到公开参数中, 实现了在标准模型和标准假设下的支持单调访问控制结构的CP-ABE, 并且密文大小仅与访问控制结构对应的单调电路大小成线性相关.另一方面,由于单调访问控制结构对应的布尔电路仅包含与门和或门, 并不完备, Ostrovsky 等[199]利用Naor 等在文献[200] 中运用的技术, 将KP-ABE 推广到了非单调访问控制结构.Okamoto 和Takashima[201]则进一步将CP-ABE 也推广到了非单调访问控制结构.

在安全性方面, 上面论述的早期ABE 方案一般都只能达到选择模型下的安全性, 如果简单使用IBE中的分割策略, 当属性空间较大时, 安全归约将指数级地松弛, 从而失效.Lewko 等[202]以合数阶群的双线性映射为代数工具, 结合双系统加密技术[203]构造出首个适应性安全的ABE.Okamoto 等[201]则引入对偶配对向量空间, 进而利用素数阶群的双线性映射模拟合数阶群的双线性映射, 同样结合双系统加密技术构造除了适应性安全的ABE.

格上的构造与群上构造的发展路线几乎一致.Agrawal 等[191]利用类似于文献[194] 中的技术, 构造出了格上第一个基于LWE 问题的门限访问控制结构的属性加密.同年, Zhang 等[204]将类似的结果推广到了CP-ABE 下.Boyen[205]基于LWE 假设构造了支持单调访问控制结构的KP-ABE, 大大扩大了格上构造的ABE 的控制策略的表达能力.Gorbunov 等[206]则更进一步, 基于LWE 假设, 将格上KP-ABE 的构造推广到了全电路(即任意多项式深度), 其密钥大小和电路大小有关, 密文大小则与电路的深度成线性相关.Boneh 等[207]结合同态加密[208]的思想, 构造了支持访问控制结构为全电路的KP-ABE, 相较于文献[206], 其最大的效率提升在于密钥的大小仅与电路的深度有关.Brakerski 等[209]则提出了支持访问控制结构为全电路的CP-ABE, 且其密文的大小仅与电路的深度有关, 但是该方案的安全性只停留在密码分析上, 没有给出安全性证明.Datta 等[210]基于LWE 假设给出了一个支持访问控制为NC1电路的CP-ABE 方案.

但是, ABE 的诸多构造主要强调的是加密消息的语义安全, 即具有载荷隐藏(payload-hiding) 的性质, 而属性集是公开的, 但在一些场合下, 属性集也希望对外保密, 即希望ABE 方案具有属性隐藏(attribute-hiding) 的性质.为了达到这样的安全要求, Katz 等[211]首先正式提出了谓词加密(predicate encryption) 的概念, 其安全模型在不可区分实验下精准刻画了属性隐藏的含义, 他们基于合数阶群的双线性映射构造了选择性安全的内积谓词加密, 并基于内积谓词加密, 给出了针对多项式、析取逻辑等谓词族的谓词加密.与ABE 的研究路线相同, 谓词加密研究的主要问题在于如何兼顾安全性的同时扩大谓词族.Lewko 等[202]利用对偶配对向量空间技术, 在素数阶群上基于n-eDDH 假设构造了适应性弱属性隐藏安全的内积谓词加密.Okamoto 等[201]利用对偶配对向量空间技术, 在素数阶群上基于DLIN 假设亦构造出适应性弱属性隐藏安全的内积谓词加密.Okamoto 等[212]开发了对偶配对向量空间下的新技术—索引(indexing) 和随机性放大(randomness amplification), 利用这些新的技术, 他们基于DLIN 假设构造了第一个适应性属性隐藏安全的内积谓词加密, 并且将该结果进一步推广到无界(unbounded) 内积谓词加密.Gorbunov 等[213]延续文献[214] 中的思想方法, 将ABE 与同态加密相结合, 基于LWE 假设构造了选择性安全但谓词族为有限深度布尔电路族的谓词加密.一个自然的问题是能否构造谓词加密方案, 其在满足较强适应性安全的同时亦可支持谓词族为更为广泛的电路族(如NC1) 的谓词加密? Bitansky 和Vaikuntanathan[215]指出适应性安全且支持的谓词族为广泛的电路族的谓词加密将直接蕴含不可区分混淆(indistinguishability obfuscation,iO).Wee[216]为了避开上述结果, 提出了部分属性隐藏这一新的安全性质, 构造了半适应性(semi-adaptive) 部分属性隐藏安全的谓词加密方案, 其在公开属性上支持的谓词族为算术分叉程序(arithmetic branching program, ABP), 在私有属性上支持的谓词族为内积函数, 首次得到了“双赢” 的谓词加密构造.Datta 等[217]利用对偶配对向量空间的方法进一步将上述结果推广到适应性安全下.

其他关于属性加密的研究主要集中在如何进一步增强属性加密功能的多样性, 以便适用于更广泛的应用场景, 例如, 类似于IBE, 如果只有一个权威可信方分发属性密钥, 那么可信方势必要对大量的用户进行服务而造成性能瓶颈, IBE 为了应对这样的场景而拓展为HIBE, 对应地, 分层次的ABE (hierarchy ABE, HABE) 也被Wang 等[218]提出, 他们将HIBE 和CP-ABE 相结合给出了HABE 的通用构造, 后续关于HABE 的工作则是如何增强HABE 的安全性[219–221].除此之外, 还有关于ABE 各种变体的研究, 比如多权威ABE[210,222,223]、注册化ABE [224,225] 等.

5.3 函数加密

自1978 年公钥加密体制问世以来, 其被广泛应用于保障机密数据的传输和存储安全.然而在经典的公钥加密体制中, 解密为完全或无(all or nothing) 的方式, 即拥有私钥能够恢复全部信息, 否则得不到任何信息.随着云计算时代的到来和隐私保护技术的发展, 要求公钥加密体制支持任意细粒度访问控制机制的需求愈发迫切.考察如下的应用场景: Alice 想通过社交网站与好友们分享合照, 希望每个好友只能看到合照中的他本人和Alice, 看不到其他人, 为了保护隐私信息, Alice 计划将合照加密后上传.显然, 经典的公钥加密体制无法满足这一需求.在此背景下, O’Neill[226]和Boneh 等[227]分别独立提出函数加密(functional encryption, FE) 的概念.简单来说, 函数加密相较于传统的公钥加密增加了函数密钥委派算法, 其可以针对函数族中的合法f(例如某个访问控制策略) 委派出函数密钥skf, 函数密钥skf的拥有方可以调用函数加密方案的解密算法从密文中计算出f(m), 而不一定是数据m本身, 从而超越了传统密码的完全或无的加解密方式.针对上述分享合照实际场景, Alice 可以作为函数加密方案的主私钥持有方, 并且根据一定的委派策略为不同好友分享不同的函数密钥skfi, 这样不同的好友仅能从加密的照片中计算出fi(m), 即为他本人和Alice 的合照.函数加密极大拓宽了公钥加密的内涵, 是传统公钥加密(PKE)、身份加密(IBE)[150,152]、可搜索公钥加密(public-key encryption with keyword searching, PEKS)[228]、模糊身份加密[194]、属性加密(ABE)[195,202]、谓词加密(predicate encryption, PE)[211,229]逐步升华泛化的结果.函数加密的强大功能性使其不仅具有重要的理论研究意义, 更使其在互联网、物联网、云计算中的自主访问控制、密文搜索、隐私保护、外包计算等领域有着广泛的应用.

就研究的函数族而言, 函数加密主要可以划分为两大类, 一类主要研究针对通用的函数族的函数加密方案, 其针对的函数族可为多项式深度布尔电路对应的函数族等, 这类研究虽然得到的密码方案功能性强大, 但往往会依赖于较沉重的密码学组件, 例如不可区分混淆(indistinguishability obfuscation,iO) 等,通常其理论意义大于现实意义.另外一类则主要研究针对特定且常用的函数族的函数加密方案, 例如内积函数、二次函数等, 其不像第一类研究中针对通用函数族的函数加密方案那样有强大的功能性, 但其构造的方案的效率、安全性却有大幅提升, 具有更大的现实意义.

• 针对通用函数族的函数加密方案: 由于抗无界(unbounded) 函数密钥腐化攻击的通用FE 难以直接构造, 早期的研究主要是在有界函数密钥腐化模型下进行考虑, Sahai 和Seyalioglu[230]首次在单次函数密钥腐化模型下, 利用混淆电路和PKE 作为基本组件构造出了针对全电路的FE.但是其密钥大小与表示函数密钥的电路大小相关, Goldwasser 等[214]以ABE 和全同态加密作为组件解决了这一问题, 使得密文大小与函数密钥对应的电路大小无关.另外一方面, 文献[231,232] 也将上述在单次函数密钥腐化模型下的构造提升到有界函数密钥腐化模型下.通用FE 构造的一个重要突破是Garg 等[233]在无界函数密钥腐化模型下, 基于iO构造的选择性安全的通用FE 方案.Boyle 等[234]则进一步基于推广的差分输入iO构造了适应性安全的通用FE 方案.而差分输入iO的构造可分别由iO[235]或多线性映射[236]给出.针对于iO的构造, 密码学界也展开了大量的研究[237–242], 其中文献[241] 指出iO可以由三线性映射或者简洁三次函数加密构造, 而最新的里程碑成果[238]中, Jain 等从四个标准假设的亚指数困难性出发构造出了亚指数安全的iO.

• 针对特定函数族的函数加密方案: Abdalla 等[243]首先研究了针对较为简单的内积函数的函数加密方案, 他们利用类似于并行ElGamal 加密的结构基于DDH 假设构造了选择性安全的内积函数加密方案, 利用类似的结构, 他们也得到了基于LWE 假设的选择性安全的内积函数加密方案.Agrawal 等[244]将文献[243] 中的密文结构改为类似于HPS 的密文结构, 并分别基于DDH、DCR、LWE 假设给出了适应性安全的内积函数加密方案.Agrawal 等[245]进一步改造文献[244]中的内积函数加密方案, 将其IND-CPA 安全性提升为SIM-CPA 安全性.理论上, 从内积函数加密出发可以朴素地构造出任意次数多项式的函数加密, 但是这种朴素构造开销过大, 比如二次函数的构造至少是平方的密文开销.另一方面, 受限于目前的密码组件多是线性, 模拟二(高) 次多项式时常会出现交叉项而难以处理, 从而二次函数加密的构造更显得困难.Baltico 等[246]利用双线性映射处理交叉项, 首次以线性的密文开销实现了选择性IND-CPA 的二次函数加密.Gay[247]提出了部分函数隐藏的内积函数加密这一新的密码原语, 并基于此给出了内积函数加密方案向二次函数加密方案的通用转换, 实现了半适应性SIM-CPA 和半适应SIM-CCA 安全的二次函数加密方案.Gong 和Qian[248]将底层线性组件模拟二次函数出现的交叉项用另一套内积函数加密方案进行封装加密, 得到了比文献[247] 开销更小的二次函数加密方案.Wee[249]则重新考虑了使用底层线性组件模拟二次函数的方式, 进一步得到了开销更小的二次函数.但是, 到目前为止, 能否在密文为线性的开销下实现适应性安全的二次函数加密仍然是一个长期的公开问题.

其他关于函数加密的研究主要集中在如何进一步增强函数加密方案功能的多样性, 以便适用于更广泛的应用场景, 例如Goldwasser 等[250]为了实现n个输入源下n个不同输入源索引的消息mi(i ∈[n])的独立加密以及协同的函数解密, 提出了多输入函数加密这一新的密码概念, 而多输入函数加密在内积函数[251–253]、二次函数[254,255]上均有深入的研究成果; 又例如一般的内积函数或者是二次函数加密方案都会在最开始固定消息向量的维度, 这并不适宜于云计算背景中的应用, 因为云服务器上存储的密文是非常大的, 但是实际上云服务器只需要对其中的一部分进行函数计算, 从而如果函数解密算法作用于整体密文, 则云服务器计算开销高昂.为了应对此种场景, Datta 等[256]提出了无界(unbounded) 内积函数加密, Tomida 和Takashima[257]基于对偶配对向量空间的方法给出了其在IND-CPA 安全性下的构造,Tomida[258]也进一步把无界性推广到二次函数加密的语境下, 并基于RO 给出了高效的构造.除此之外,函数加密还有诸如多权威[259]、去中心化[260,261]、多层次[262]等更丰富功能性下的扩展变体.

5.4 可搜索加密

函数加密强大的功能性使得函数密钥的拥有方能够做指定的函数运算以知道消息的函数值, 其安全性则保证了函数密钥的拥有方除了消息的函数值外一无所知.这样的特点使得函数加密这一密码原语拥有广泛的应用场景, 例如, 考虑如下云存储的场景: 医疗机构将巨量加密后的病历及其对应的关键词索引等数据存储在云服务器上, 除此之外, 医疗机构也希望能够通过与云服务器交互, 在加密的数据上检索任何一位病人的病历数据, 且不会泄漏关于病例数据的明文的任何有效知识给云服务器和第三方.显然,理论上来说, 针对全电路/图灵机的函数加密可以完美地实现上述场景, 但是由于其存在性依赖于沉重的密码组件, 极大的计算开销和查询复杂度使得其很难应用到现实生产环境中.另一方面, 在加密数据上进行检索又是现实中非常普遍的、亟需解决的问题, Song 等[263]针对这样的场景, 首次提出了可搜索加密(searchable encryption, SE) 的概念, 并利用对称加密构造了非常高效的可搜索加密方案.从此之后, 可搜索加密飞速发展, 其上研究主要可以分为基于对称加密的对称可搜索加密(symmetric searchable encryption, SSE), 以及基于公钥加密的非对称可搜索加密(asymmetric searchable encryption, ASE), 下面将主要介绍ASE 方面的研究成果.

Boneh 等[228]首次将可搜索加密引入了公钥密码学的领域, 为其建立了基本的语义和形式化的安全模型, 并分别基于双线性映射和陷门置换函数构造了第一个基于公钥加密的关键词可搜索方案(publickey encryption with keyword searching, PEKS).Abdalla 等[264]则注意到身份加密中的身份和搜索关键词的关联性, 给出了匿名IBE 方案到PEKS 方案的通用转换.但是以上关于ASE 的工作都是针对单关键词的可搜索加密, 现实中的搜索应该支持更为丰富的高级搜索选项, 例如多个关键词、区间搜索、模糊搜索等.Golle 等[265]重新定义了基于公钥加密下的可搜索加密的语义, 将其推广到了支持多个关键词的搜索, 并基于DDH 假设构造了通信复杂度与数据库中的数据量成线性关系的可搜索加密方案.Boneh等[229]提出隐藏向量加密(hidden vector encryption, HVE) 这一新的密码原语, 并基于该原语分别给出了支持多关键词、区间搜索、子集检索的高效简洁的可搜索加密方案的通用构造框架.在安全模型上,Baek 等[266]注意到一般在讨论可搜索加密的时候[228,264]都是单独考虑关键词域的安全性, 他们认为这样安全模型并不完整, 因此将关键词域部分的PEKS 和对应的数据域部分的PKE 作为一个整体, 同时考虑其安全性, 定义了PKE-PEKS 的安全模型.Zhang 等[267]则注意到Baek 定义的PKE-PEKS 的安全模型忽略了关键词域部分的安全性, 重新定义了PKE-PEKS 的安全模型.Bellare 等[268]进一步注意到在CCA 安全下不仅仅需要考虑PKE 解密谕言机的信息泄漏, 还需要额外考虑PEKS 的关键词匹配谕言机的额外信息泄漏, 从而再度增强了PKE-PEKS 安全模型, 并利用基于标签的CCA 安全的PKE 方案和PEKS 方案给出了满足增强安全性后的PKE-PEKS 方案.Chen 等[269]则是改进了Bellare 等[268]的构造, 给出了从匿名HIBE 到PKE-PEKS 的通用构造, 其密钥大小约为文献[268] 中的一半.后续的工作则是进一步细化关键词的搜索匹配模式, 比如针对于不同度量距离(如汉明距离、编辑距离等) 下的模糊搜索[270–273], 除此之外, 还有一系列工作是将可搜索加密推广到更广泛的使用场景下(例如多用户等) [274,275].

以上构造可搜索加密的底层公钥加密方案几乎都是概率性加密算法, 虽然得到的安全性较高, 但是云存储服务器的查询复杂度一般都与数据库中的数据量成线性关系, 针对存储着大量加密数据的云服务器, 这样的查询复杂度是无法接受的.另外一条实现可搜索加密的路径是使用确定性加密(deterministic encryption) 方案.Bellare 等[276]提出了确定性公钥加密, 形式化了其PRIV 安全模型, 并利用“以哈希值作为加密随机数(encrypt with hash)” 的技术构造了PRIV 安全的确定性公钥加密.除此之外, 他们利用PRIV 安全的确定性加密方案给出了高效可搜索方案的通用构造, 其思想极简洁: 对关键字域做哈希运算得到关键字的短标签, 然后将关键字用上述技术进行确定性加密就可以得到高效的可搜索加密(存储相应的短标签和关键字的密文可以采用树状数据结构).接收者若要查询相应的关键字, 可以直接计算关键字的哈希值得到其短标签, 云存储服务器根据短标签的值可以采用类似于二分查找的方法快速定位相应的关键字, 其查询复杂度仅为数据量的对数级别.最开始满足PRIV 安全性的确定性加密方案是在随机谕言机(RO) 下进行构造的, 而Boldyreva 等[277]利用文献[41] 中的技术在较弱的PRIV1 安全模型下给出了标准模型和标准假设下的构造.Bellare 等[278]进一步详细讨论了确定性加密不同安全性的等价关系,给出了更多的构造.事实上, 如果关键字域的最小熵较小, 那么基于确定性加密的可搜索加密会遭受暴力遍历攻击, 并且Bellare[276]定义的安全模型是选择性的模型, 而非适应性的模型, 所以如何为确定性加密定义更强的安全模型并给出相应的构造是后续研究的主要关注点, 一系列的工作均围绕此展开[279–284].

5.5 (全) 同态加密

身份加密、属性加密、函数加密、可搜索加密的解密过程可以统一理解为用私钥对密文进行秘密计算, 计算的结果为明文.从而, 即使是极致泛化的函数加密也无法对密文进行有意义的计算(在不拥有函数密钥的情况下), 也就很难将数据的计算外包给半诚实或者恶意的云服务器.事实上, Rivest 等[285]就提出一个问题—“能否在保护数据隐私的同时实现数据的外包计算？” 这样的问题在现实应用中是非常普遍的, 比如, 某个医疗机构想要对内部采集的保密且巨量的基因数据进行分析, 显然分析带来的巨大计算开销是普通机构无法承受的, 这时, 在保证数据不泄漏的情况下实现相应的计算任务就显得极为重要.围绕(全) 同态加密的研究正是为了能解决这样的问题, 并且是以更省、更快、更普遍的方式加以解决.

根据可计算的函数类型, 同态加密的方案可分为部分同态加密和全同态加密(fully homomorphic encryption, FHE), 其中全同态的加密方案支持任意深度的电路, 而部分同态的加密方案仅支持非常受限类型的电路.事实上, 部分同态的PKE 方案很早就存在, 例如Goldwasser 等[286]的GM 加密方案即支持模2 上的无限制次数的加法运算, 又例如Rivest 等[10]的RSA 加密方案即支持Z∗N上无限制次数的乘法运算.后续有很多方案在部分同态上走得更远, 例如Boneh 等[287]的基于双线性映射的PKE 方案可以支持有限域上无限制次数的加法和仅一次乘法, Sander 等[288]的PKE 方案可以支持对数深度的电路(即NC1).部分同态的加密方案要么存在着密文随着同态运算次数的增多而快速膨胀的问题, 要么存在着仅能支持一种运算、或者有限次运算的问题.2009 年Gentry[289]基于理想格提出了真正意义上的全同态加密, 这是全同态加密领域的一个里程碑式的研究成果, 此后, 各种全同态加密方案被陆续提出, 下面按照四个世代对其展开阐述.

• 第一代全同态加密: Gentry[289]提出了第一个全同态加密方案, 其中的关键为自举(bootstrapping) 技术, 该技术可以在保证不损坏同态性的同时减少噪声从而使得密文合法, 即可以正确解密,该技术可以将某些具有自举性质的部分同态的加密算法转换为全同态加密算法, Gentry 基于理想格上的困难问题构造了满足自举性质的部分同态加密方案, 然后将其自举, 得到了全同态加密方案.Gentry 的全同态加密方案虽然是理论上的一大突破, 但是实际运行效率并不高, 每比特运算需要耗时30 分钟[290].Van Dijk 等[291]将文献[289] 底层的基于理想格的部分同态加密方案换为基于整数的部分同态加密方案, 并沿用Gentry 的技术路线, 得到了第二个全同态加密方案.

• 第二代全同态加密: Brakerski 和Vaikuntanathan[292,293]革命性地改进了自举技术, 在标准格上基于(R)LWE 假设以及循环安全假设(circular security assumption) 构造了两个新的全同态加密方案, 他们引入了两个非常重要的技术, 即重线性化技术(re-linearization) 与模缩减(modulus reduction) 技术.重线性化技术可以压缩密文的大小, 防止其过度膨胀, 模缩减则可以将部分同态的密码方案转换为全同态的密码方案, 该技术将较大模下的密文转换为较小模下的另一密文, 引入的噪声更小, 也不需要利用稀疏子集困难问题进一步压缩电路, 更加高效.Brakerski 等[294]则进一步提出支持有限深度电路的层次化的全同态加密的概念, 使得全同态加密在一定程度上摆脱了计算开销较大的自举技术, 大幅提高了效率.后续的工作则进一步通过引入并行化、打包、批处理[295,296]等优化技术, 使得效率进一步提高.而近期相关的研究则是仅基于RLWE 假设, 在多项式环上实现上述BGV 方案[294]的变体, 效率更优[297,298].

• 第三代全同态加密: Gentry 等[208]利用新的技术—近似特征向量方法(approximate eigenvector method), 避免了重线性化给乘法带来的较大噪声.Brakerski 和Vaikuntanathan[299]则注意到对于特殊的电路, GSW 方案[208]的噪声增长速度更慢, 从而给出了更高效和更安全的实现, 该全同态加密方案基于多项式近似的GapSVP 假设.Alperin-Sheriff 和Peikert[300]进一步基于此观察, 同时结合FFT (fast Fourier transform) 算法等优化方法, 得到了具有高效的自举过程的全同态加密方案.Chillotti 等[301]基于文献[300] 的思想, 利用另外一种自举方式[302]得到了极其高效的实现, 其自举一个比特仅需要12 ms.

• 第四代全同态加密: Cheon 等[303]提出了可以支持某些浮点运算的分层次全同态加密方案, 而浮点运算是诸多工业应用(例如训练神经网络) 所需要的, 这使得分层次全同态加密具备了落地实用的可能.次年, 他们[304]又将类似结果推广到了全同态加密下.后续的工作则进一步研究了CKKS 方案的更优化的实现[305,306], 例如支持打包等操作.Li 和Micciancio[307]讨论了CKKS方案[303]在被动攻击下的安全性, 他们指出在部分场景下, IND-CPA 安全性可能并不足够, 并给出了一些具体的攻击.关于Li 和Micciancio[307]的攻击, 一些修补方法也陆续被提出[308].

总的来说, 自从Gentry[289]在2009 年提出第一个全同态加密方案后, 全同态加密的研究主要是对自举技术不断改进, 将自举开销从分钟量级[290]最终降低到毫秒量级[309], Rivest 等[285]的愿景终于成为现实.

6 前沿进展与新方向

6.1 公钥加密选择密文安全的复杂度下界

公钥加密中一个重要的公开问题是: CPA 安全的PKE 是否在黑盒意义下蕴含CCA 安全的PKE?近年的一系列前沿工作正式围绕这一问题展开.Koppula 和Waters[310]提出了hinting PRG (带提示的伪随机数生成器), 并以此为工具给出了CPA 安全PKE 到CCA 安全PKE 的黑盒转换.该结果并未解决公开问题, 因为目前已知的hinting PRG 构造仍需依赖CDH 假设、大整数分解假设或LWE 假设.根据已知的结果, 标准的单射单向陷门函数蕴含CPA 安全的PKE, 具有丰富性质的单向陷门函数(如信息有损、相关积安全) 可以蕴含CCA 安全的PKE.Hohenberger 等[43]向着公开问题迈出了重要的一步,证明了标准的单射单向陷门函数即可蕴含CCA 安全的PKE.此后, 只需证明CPA 安全的PKE 蕴含单射单向陷门函数即可彻底解决公开问题.Garg 等[311]展示了结合具有伪随机密文性质的CPA 安全加密和hinting PRG 即可构造出单向陷门函数.因此, 我们认为今后研究的焦点将围绕探寻构造hinting PRG所需最弱假设展开.

6.2 细粒度模型下的公钥加密

传统密码学中, 几乎所有私钥密码方案的安全性都至少依赖单向函数的存在性, 而公钥加密等公钥密码方案则依赖输入同态弱不可预测函数等更强的密码原语或者整数分解类、Diffie-Hellman 类等具体的结构化数学假设.然而, 至今单向函数是否存在仍是密码学领域乃至整个计算复杂性领域中一个悬而未决的问题, 更遑论公钥加密方案.随着密码分析技术的发展, 更强的密码原语或结构化数学假设一旦被攻破, 现有的公钥加密大厦恐将瞬间坍塌.

为缓解上述威胁, Merkle[312]于1978 年开启了关于细粒度模型下的密码学(fine-grained cryptography) 的研究.细粒度模型下的密码学旨在根据实际情况针对(如计算量、存储量或算法回路深度等) 运算资源相对受限的攻击者进行更精细的划分和定义, 并要求: (1) 只基于非常弱的假设甚至不基于任何假设针对精细定义的攻击者设计安全的密码方案; (2) 用户运行方案时所消耗的资源不超过攻击者所消耗的资源, 以保证密码方案能高效运行.一般情况下, 运行该类密码方案所消耗的资源远少于传统密码方案, 因此, 虽只考虑资源有限的攻击者, 该模型下的密码仍具有广泛的实用价值.例如, 细粒度模型下的签名能保证攻击者伪造签名须消耗一定时长, 因此能在降低成本的同时通过拒绝签名超时的用户来过滤攻击者; 而细粒度模型下的加密能以极低的成本加密具有实效性的信息.此外, 通过利用双层加密等手段将细粒度模型下的密码方案与传统密码方案相结合, 可立即得到在强假设下能抵御任意的多项式攻击者且在弱假设下能抵御资源相对受限的攻击者的混合密码方案.下面将重点介绍细粒度模型下公钥加密领域的代表性成果.

Merkle[312]在随机谕言机模型下提出了非交互密钥交换协议, 其运行的时间复杂度为O(n) 并能抵御时间复杂度为O(n2) 的攻击; Biham 等[313]则基于强单向函数实现了同样的方案; LaVigne 等[314]基于zerok-clique 实现的私钥交换协议可抵御复杂度为O(n1.5) 的攻击者.这些方案都可被转换为细粒度模型下的公钥加密.Degwekar 等[315]基于被广泛认可的最坏复杂假设NC1⊊⊕L/poly 针对NC1(即深度为O(logn) 且由多项式个扇入2 的与、或、非门组成的回路集合) 的攻击者构造了一个满足INDCPA 安全性且能在AC0[2] (即常数深度且由多项式个无限扇入与、或、非、异或门组成的回路集合, 注:AC0[2] ⊊NC1) 中运行的公钥加密方案.在同样的细粒度模型下, Campanelli 和Gennaro[316]提出了准同态公钥加密方案; Egashira 等[317]提出了细粒度模型下的单向陷门函数与满足IND-CCA 安全性的公钥加密方案, 并进一步提出了该模型下的全域单向陷门函数[317]; Wang 等[318]提出了该模型下的属性基加密方案以及QA-NIZK, 前者可被实力化为针对多种谓词函数的属性基加密、广播加密、身份加密以及模糊身份加密, 后者可用于实现带有公开验证机制的细粒度IND-CCA 加密; Wang 和Pan[319]则提出了该模型下的全同态公钥加密方案.研究如何基于不同的弱假设使密码原语抵御更大范围的攻击者以及如何在实现相同安全性的前提进一步弱化假设会是细粒度模型下的重要课题.

除了以上提及的两个前沿方向外, 抗量子攻击的公钥加密方案是学术界和产业界共同关注的热点与焦点, 关于这方面的前沿进展请参阅文献[320].