新形态对称密码算法研究*

吴文玲, 王博琳

1.中国科学院 软件研究所, 北京 100190

2.中国科学院大学, 北京 100049

1 引言

数据安全与人们的生产生活已密不可分, 从飞机、汽车的设计制造, 到个人生活点滴的记录, 数据已渗透到人类社会的各个方面.大数据时代的数据安全不仅包括传统的机密性、完整性、可用性等, 也包括隐私保护; 不仅包括防止数据泄露的隐私保护, 也包括数据分析意义下的隐私保护.数据安全问题的解决需要有可信赖的技术手段支持, 近年来, 涌现出一大批数据安全新技术, 包括具体高效的安全多方计算技术、同态加密、函数加密、差分隐私保护技术、可验证计算技术、零信任技术等.

安全多方计算(secure multi-party computation, MPC) 由姚期智先生于1982 年通过提出并解答百万富翁问题而创立, 能够在不泄露任何隐私数据的情况下让多方数据共同参与计算, 然后获得准确的结果,可以使多个非互信主体在数据相互保密的前提下进行高效数据融合计算, 达到数据可用不可见.基于秘密分享的MPC 协议的参与方可以利用本地拥有的份额进行加法、数乘的计算, 不需要与其他参与方进行交互和通信, 协议通信主要发生在乘法门计算, 所有运算定义在有限域上, 也可推广至一般环上.为了让数据安全地进出基于秘密分享的MPC 协议, 一种有效的解决方案是直接使用系统内的对称密码算法进行计算.然而, 基于AES 或SHA-3 的伪随机函数(PRF) 在此应用场景的性能不好.主要问题是数据类型不匹配, MPC 的数据通常表示为有限域Fp上的元素, 而AES 和SHA-3 的数据都表示为比特串; 虽然两者可以转换, 但代价昂贵; 当底层引擎执行算术模运算时, 数据格式转换将极大影响MPC 的实现性能.因此, MPC 需要基于算术运算的对称密码算法.在MPC 中使用现有对称密码算法标准, 其实现性能和通用实现性能差距很大.比如, 在X86 等处理器上, AES 可以在100 个时钟周期内完成一次分组加密, 而在MPC 中实现相同的密码运算需要数十亿个时钟周期.主要原因在于, 在X86 等处理器上实现线性运算(XOR) 和非线性运算(AND) 的成本差别不大, 而MPC 的情况完全不同.线性运算几乎是免费的, 只进行本地计算, 不会增加太多噪声, 而涉及对称密码算法和各方交互的非线性运算会显著增加噪声.因此,面向安全多方计算设计对称密码算法时, 希望算法中的非线性运算个数尽可能少.分组密码LowMC 是第一个适宜MPC 的对称密码算法.2020 年, Rechberger 等人发起了LowMC 分析挑战赛, 吸引了许多密码学者的研究兴趣.随着MPC 的发展及其应用需求的推动, 一些适宜MPC 的新形态对称密码算法应运而生, 如MiMC 及其变体、Ciminion 和HYDRA 等.

同态加密(homomorphic encryption, HE) 方案指能够对加密数据进行加法或乘法操作而不需要解密密钥的加密方案.全同态加密(fully homomorphic encryption, FHE) 是指同时满足加法同态和乘法同态性质, 可以进行任意多次加法和乘法运算的加密函数.2009 年, Gentry 基于理想格上的困难问题构造了第一个可行的全同态加密方案, 随后发展出了基于不同安全假设的全同态加密方案, 比如BGV、BFV 和GSW 方案.尽管在效率方面已有较大提升, 但仍未脱离Gentry 所提出的构造全同态加密方案的理论框架, 首先构造一个部分同态加密方案, 之后再通过自举来实现全同态加密.考虑到部分同态加密方案的安全性, 加密过程需要引入噪声; 随着同态运算的进行, 噪声不断地累积, 一旦噪音的尺寸超出某个阈值, 就会出现解密错误.通常, 乘法运算引起的噪声大于加法的噪声.因此, 大多数情况下全同态加密方案参数化时, 需要评估所要考虑的布尔电路的乘法深度.乘法深度指的是可以在密文上执行的连续同态乘法的最大数量, 许多全同态加密方案的噪声随着电路的乘法深度而快速增长.因此, 面向全同态加密的对称密码算法, 设计目标首先是最小化乘法深度.其次, 虽然某些特定应用程序的同态操作的成本取决于密码的乘法深度, 但计算额外解密电路本身的代价主要取决于乘法数量.因此, 尽量减少乘法门的数量也是适宜全同态加密的对称密码算法的设计指标.除了噪声问题, 全同态加密方案还存在密文扩展问题, 严重影响其在带宽、存储和计算能力有限的场景落地应用.许多云服务应用框架组合使用对称加密算法和非对称同态加密方案, 以AES 作为对称密码的实例算法, AES 解密计算的乘法深度成为一个瓶颈, 因此, 亟需面向全同态加密的对称密码算法.近几年推出的对称密码算法有: Kreyvium、FLIP、Rasta 及其变体、Pasta、Chaghri 和Rubato 等.

零知识证明(zero-knowledge proof, ZK) 是由Goldwasser 等人在20 世纪80 年代初提出的, 指的是证明者能够在不向验证者提供任何有用信息的情况下, 使验证者相信某个论断是正确的.零知识证明不仅作为一个基本工具为实现各种密码协议分析与构造提供强有力的支持, 而且其证明方法也成为一种方法论被广泛使用.在零知识证明系统中, 需要将计算问题编码为有限域上的代数约束满足问题, 这一过程称为算术化(arithmetization), 目前常用的算术化方法是R1CS、Plonk 和AIR 等三类.近些年使用广泛的证明系统分为ZK-SNARKs 和ZK-STARKs 两种, 它们采用不同的算术化方法进行描述, ZK-SNARKs基于R1CS 和Plonk 两类算术化方法, 而ZK-STARKs 基于AIR 方法, 因此证明大小和生成时间的计算方式均不同.在ZK-SNARKs 中, 证明代价与执行的非线性操作的数量成正比; 而在ZK-STARKs 中,证明代价与必须验证的电路的次数和深度有关.因此, 零知识证明系统通常需要选取针对乘法数量和乘法深度可以优化实现的对称密码算法, 具体的优化目标取决于应用场景的需求.此外, 在许多此类应用中, 需要使用定义在奇特征有限域上的杂凑函数, 特别是素域上的杂凑函数.例如, 部署在Zcash 的零知识证明系统.近些年陆续推出了一系列与相关应用环境相匹配的新形态对称密码算法, 例如Jarvis、Friday、Vision、Rescue、POSEIDON、STARKAD 以及Reinforced Concrete.对以上算法的研究也在如火如荼地进行着, 如2020 年发起的“STARK-Friendly Hash Challenge” 挑战和2021 年以太坊基金设立的包括POSEIDON 在内的几种适宜零知识证明的对称密码算法挑战赛.

综上可知, 安全多方计算、全同态加密和零知识证明为对称密码算法提出了一些新的性能指标, 而AES 等现有标准算法不能满足这些需求.因此, 近些年国际上推出了一批与相关应用相匹配的新形态对称密码算法.不同于现有的对称密码算法标准, 此类算法更强调算术运算, 如环上的运算、有限域Fp及F2n上的运算等, 且在利用该类算法时, 均需将其转换为代数问题, 并经历一个算术化的过程, 这个过程在本质上是相似的, 因此统称它们为面向算术化的对称密码算法.新形态对称密码算法通常关注以下三个性能指标.一是乘法复杂度(MC), 一般指电路中的乘法数量(AND 门数量); 二是每个加密比特的AND 门数量(MC/bit); 三是电路的乘法深度(ANDdepth).除了以上性能指标, 设计算法时还需要综合考虑特殊结构及状态大小等因素的影响.本文根据应用场景对新形态对称密码算法分类介绍, 但一些算法在设计时关注了多个性能指标, 因而同时适用于多种应用场景, 如LowMC 同时适用于MPC 和FHE, MiMC 同时适宜MPC 和ZK.表1 总结了不同类型新形态对称密码算法的运算所在有限域及适宜的应用场景.

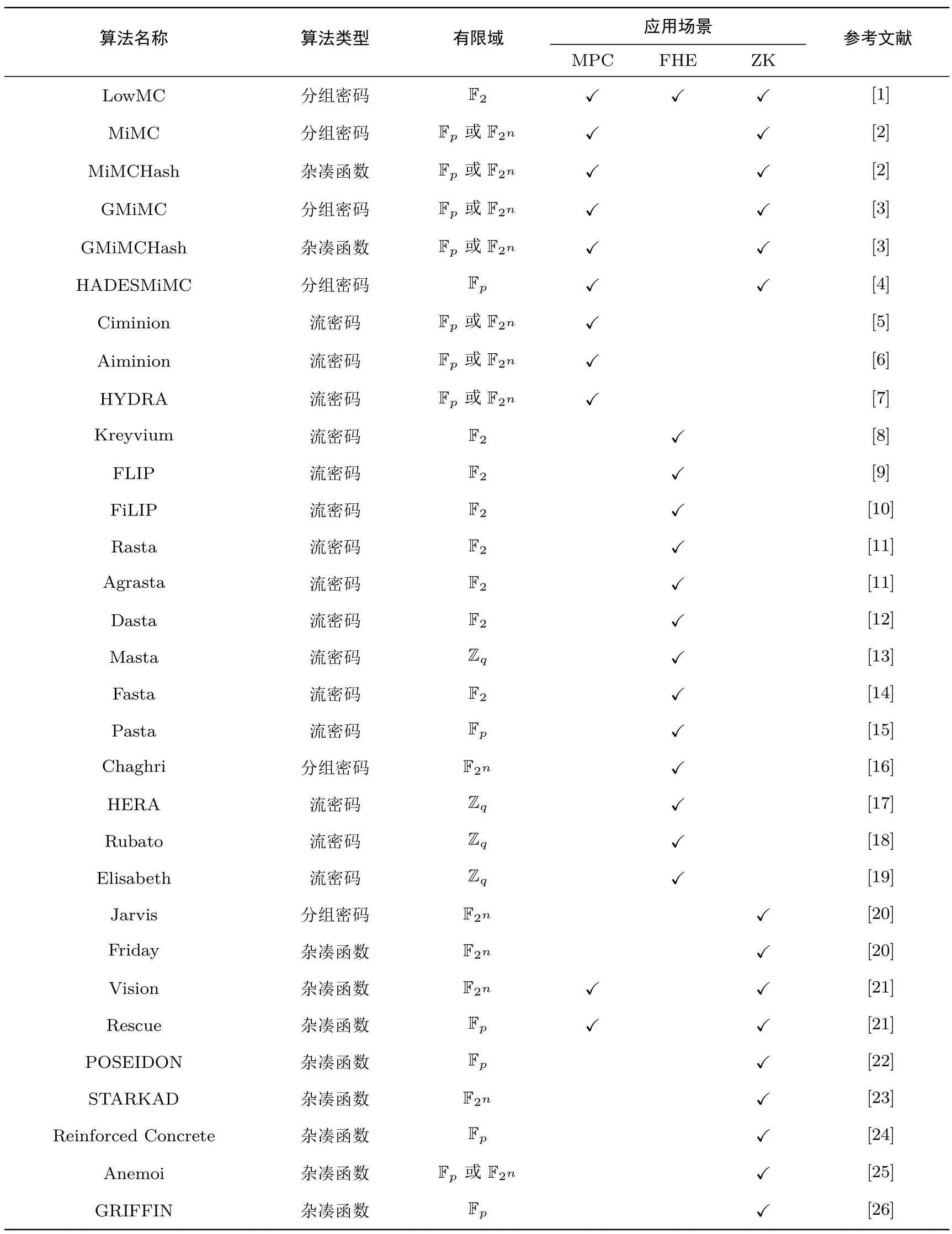
表1 新形态对称密码算法Table 1 New morphologic symmetric cryptographic algorithms

本文的组织结构安排如下: 第2 节、第3 节和第4 节分别介绍了适宜MPC、FHE 及ZK 的新形态对称密码算法, 第5 节总结新形态对称密码算法的特点以及面临的问题.

2 适宜MPC 的对称密码算法

2.1 LowMC

2015 年, Albrecht 等提出了P-SPN 结构的分组密码LowMC[1].P-SPN 结构又称为部分SPN 结构, 该结构在算法每一轮的非线性层中只有一部分使用非线性S 盒的变换, 其余部分均为恒等变换.作为第一个新形态对称密码, LowMC 吸引了密码学界的大量关注.LowMC 的轮函数包括四个操作: S 盒层、线性层、轮常量异或及轮密钥异或.S 盒层采用3 比特S 盒, 线性层使用基于比特操作的n×n的二进制矩阵.它的特点是用户可以根据需求自主选择参数(每轮S 盒数量、线性层、轮常量、密钥编排函数) 来进行实例化.LowMC 设计的亮点在于S 盒层减少了并行S 盒的数量, 即采用部分S 盒的设计来降低乘法复杂度, 为了在低乘法复杂度的情况下满足安全性要求, 在线性层中使用伪随机生成的二进制可逆矩阵.除此之外, 轮常量及轮密钥也是随机生成的.Albrecht 提出了两个具体实例.第一组采用80 比特密钥提供“类似于PRESENT” 的安全性, 而第二组采用128 比特密钥提供“类似于AES” 的安全性.在MPC和FHE 的实现方面, 当加密大量数据时, LowMC 在计算和通信复杂度方面均有不同程度的改进.在乘法复杂度和乘法深度方面, 最接近的竞争对手分别是Simon 和PRINCE.

LowMC 自提出后不久, 就出现了对其的高阶差分攻击[27]和插值攻击[28], 这两种攻击均需要很多选择明文.为了抵抗这些攻击, 设计者推出了LowMC v2 版本, 即使用新的公式来确定安全轮数.2018 年,Rechberger 等人[29]提出了利用差分枚举中间相遇攻击分析LowMC v2 的多个实例, 导致了LowMC v3版本的出现.2021 年, Liu 等人[30]结合差分枚举技术和代数攻击, 仅用2 个选择明文和可忽略的内存复杂度就可以对LowMC v3 的一些实例进行分析.此外, 选择2 个明文对LowMC 的攻击可以扩展到对LowMC-M 使用大量选择明文进行攻击, 这些分析使得LowMC-M[31]的设计者增加了轮数.之后, Liu等人进一步改进对LowMC 的差分枚举攻击, 提出了代数中间相遇攻击[32].Rechberger 等人[29]的差分枚举中间相遇攻击的存储复杂度是攻击轮数的指数, 虽然代数攻击[30]可以使存储复杂度忽略不计, 但攻击轮数有限.代数中间相遇攻击不仅可以降低差分枚举中间相遇攻击[29]的存储复杂度, 与代数攻击[30]相比, 还可以通过使用额外的内存来提高攻击轮数, 并且适用于各种LowMC 参数的实例.2023 年, Qiao等人[33]针对完整S 盒层的LowMC 实例, 提出了一种新的差分枚举攻击框架, 该方法不再考虑传统的差分, 转而考虑2-差分.利用代数方法枚举2-差分, 并用线性化技术从恢复的2-差分迹中恢复密钥.将攻击应用于分组大小分别为129、192 和255 比特的4 轮LowMC, 攻击的数据复杂度均为3 个选择明文.与Liu 等人的攻击[30]相比, 在时间复杂度或成功概率方面有所改进.

LowMC 系列分组密码的主要应用之一是用于后量子签名方案PICNIC 中.PICNIC 在实例化时需要一个具有较低计算开销的函数, 这种开销在很大程度上取决于计算函数所需的非线性运算的数量, 即乘法数量.LowMC 是一种专门针对FHE 和MPC 设计的高效分组密码, 旨在最大限度地减少乘法数量,这使得LowMC 成为PICNIC 实例化的十分合适的选择.令E(K,pt) 为使用密钥K对明文pt 进行的LowMC 加密.明文/密文对(pt,ct =E(K,pt)) 用作签名方案的公钥(验证密钥), 加密密钥K用作秘密密钥(签名密钥).如果攻击者可以在仅给定单个明文/密文对(pt,ct), 即签名方案的公钥的情况下恢复加密密钥, 则实际上他可以计算出秘密签名密钥, 进而允许他通过使用恢复的签名密钥来伪造签名.因此, 在单个明文/密文对背景下对LowMC 分组密码的密钥恢复攻击会直接影响PICNIC 签名方案的安全性.2020 年5 月, 在微软等公司的资金支持下, 知名学者Rechberger 等人发起了LowMC 算法分析挑战赛[34], 尤其针对应用于PICNIC 底层的LowMC 算法实例, 以此促进LowMC 算法及PICNIC 方案的研究发展.有三个团队在这种攻击场景中提出了针对LowMC 的新攻击[35–38].根据第三轮结果的公布,中间相遇方法[36]和多项式方法[37]的攻击被选为目前最好的攻击, 但这两种方法的一个共同特点是消耗大量内存.后来, Banik 等人[39]结合了文献[36] 中的线性化技术和文献[37] 中的方程求解方法, 分析了具有完整S 盒层的LowMC 实例, 大大降低了内存复杂度.之后, Liu 等人[40]通过使用更好的时间存储折中策略, 进一步显著改进了PICNIC 背景下对LowMC 的攻击.

2.2 MiMC 及其变体

(1) MiMC

2016 年, Albrecht 等给出了定义在有限域F2n或Fp上的以最小化乘法复杂度为目标的对称密码系列MiMC[2].MiMC 包括: 分组密码MiMC-n/n和MiMC-2n/n、杂凑函数MiMCHash.分组密码MiMC-n/n直接通过函数F(x)=x3和轮子密钥及轮常量实现加密.分组密码MiMC-2n/n在Feistel 结构中使用与MiMC-n/n相同的非线性置换F(x) =x3进行加密, 记为Feistel-MiMC, 且轮数为MiMCn/n轮数的2 倍.杂凑函数MiMCHash 是在Sponge 结构中实例化置换MiMC-n/n得到的.MiMC 作为适宜MPC 的PRF 是一个非常有竞争力的候选者.与AES 相比, 测试结果表明, MiMC 在线阶段的吞吐量高出10 倍以上, 在LAN 设置中的离线/预计算阶段仍然快约6 倍.由于MiMC 的串行性质和相对较高的轮数, 延迟可能会相对较高, 但也优于AES 的延迟.

(2) GMiMC

2019 年, Albrecht 进一步推广MiMC 中使用的设计方法, 他们使用两个非平衡的Feistel 结构和一个新的平衡Feistel 结构来构造一个新的分组密码系列—GMiMC[3], 包括GMiMCcrf、GMiMCerf和GMiMCmrf, 并用它来在Sponge 结构中构造杂凑函数GMiMCHash.在MPC 中, GMiMC 的吞吐量与MiMC 相比提高了4 倍以上, 同时预处理工作减少了80% 以上, 尽管以更高的延迟为代价.在SNARK应用程序中, GMiMCerf在三种结构中的性能最好.对于N ≈1024 比特分组大小的GMiMCerf, 当t=8时, 观察到其比MiMC-1025 有所改进.对于单个消息分组, GMiMCHash-256 比MiMCHash-256 快1.2倍以上.与MiMCHash 相比, GMiMCerfHash 的主要优势是它可以使用超过256 位或更小的素域.在最近提出的基于ZK 的后量子密码签名方案领域, LowMC 被认为是小签名和运行时间的最佳选择.由于可以灵活选择分支数, GMiMC 与LowMC 相比具有一定的竞争力, 并且比MiMC 效率高得多, 其签名大小约为MiMC 的三十分之一.

(3) HADESMiMC

2020 年, Grassi 等提出了将经典SPN 结构与P-SPN 结构相结合的HADES 结构[4].该结构将整体轮数分为三部分: 中间部分为P-SPN 结构, 两边为相同轮数的SPN 结构.一方面, 为了确保算法针对差分和线性密码分析的安全性, 在开始和最后使用SPN 结构.另一方面, 为了尽可能减少非线性操作的总数, 在中间部分使用P-SPN 结构(通常情况下非线性层使用一个S 盒), 这样不仅可以达到较高的代数次数, 还可以尽可能地满足低乘法复杂度的要求.最后, 通过选择完整S 盒层和部分S 盒层的轮数之间的最佳比例, 可以同时实现安全性和性能要求.由以上方法得到的HADES 结构不仅可以直接使用宽轨迹策略进行分析, 还可以针对代数攻击给出安全性声明.

分组密码HADESMiMC 是Grassi 等基于HADES 结构给出的在素域Fp上设计的面向MPC 的一个实例.轮函数由三部分组成: S 盒层、线性层和轮密钥加, 其中S 盒采用的是幂函数S-Box(x)=x3.线性层使用基于字操作的MDS 矩阵, 密钥编排函数是线性的.在使用安全多方计算保护分布式数据库的数据传输中, 与目前最快的MiMC 相比, HADESMiMC 的在线带宽要求和吞吐量显著提高, 并减少了预处理工作, 同时具有相当的在线延迟.

2019 年, Li 和Preneel[41]提出了对MiMC 的插值攻击, 这是对MiMC 的第一个第三方分析.与MiMC 设计文档里给出的经典插值攻击相比, 攻击只需要常数大小的存储或数据复杂度.对于具有82 轮的MiMC-129/129, 可以破解38 轮, 数据和时间复杂度分别为265.5和260.2, 存储复杂度可忽略.对于具有较大密钥的MiMC 变体, 该攻击的复杂度更低.除此之外, 作者还提出了对具有简单密钥编排的分组密码的通用插值攻击.2020 年, Eichlseder 等人[42]给出了定义在F2n上的接近全轮MiMC 的高阶差分区分器和接近MiMC 两倍轮数的已知密钥零和区分器, 以及F2n上全轮MiMC 的密钥恢复攻击和具有低次数轮函数的密钥交替密码的代数次数增长的新上界.

2020 年, Roy 等人[43]将文献[41] 的低内存插值攻击扩展到具有低次数函数的非平衡Feistel 结构, 并将其应用于GMiMC.之后他们给出了针对具有扩展轮函数的GMiMC 的有效密钥恢复技术, 并表明最终的密钥恢复步骤不仅可以简化为GCD 问题, 还可以简化为求根问题.Beyne 等人[44]给出了GMiMCerf和HADESMiMC 置换的低复杂度积分区分器和零和区分器.在ZK-STARKs 中时, 针对实际使用的Sponge 结构的具体设置, 给出了GMiMC 置换的缩减轮的实际碰撞攻击.除此之外, 他们还将这几种密码技术推广到了奇特征的有限域.2022 年, Beyne 等人[45]利用截断差分密码分析, 得到了对收缩型Feistel 结构密码的改进通用攻击.当应用于GMiMCcrf时, 上述攻击对于某些实例可以得到全轮区分器和密钥恢复攻击.然而, 这些攻击的实际意义可能相对有限, 因为GMiMCcrf的大多数应用程序使用的分支数量t相对较小, 但选取的有限域很大.Cui 等人[46]将二元域上的可分性质推广到有限域F2n上, 给出了一种对基于算术运算的密码代数次数进行检测的通用方法.主要思想是评估分组密码的多项式表示是否包含某些特定的单项式.在深入研究基于域运算的算法特征的基础上, 引入了基于域运算的单项式传播规则, 并利用SMT 的比特向量理论对其进行了有效建模.利用代数次数与单项式指数之间的关系,构造了一种新的次数估计搜索工具.之后, 将上述方法应用于Feistel-MiMC、GMiMC 和MiMC.对于Feistel-MiMC, 结果表明代数次数的增长明显低于指数界, 并首次提出了一种高达124 轮的秘密密钥高阶差分区分器, 比Beyne 等人[44]对Feistel-MiMC 置换给出的83 轮区分器要多41 轮.此外, 还给出了一个已知密钥条件下的全轮零和区分器, 数据复杂度为2251.将以上方法扩展到更多的分支, 成功地找到了目前最长的秘密密钥高阶差分区分器, 可用于分组密码GMiMCerf的实际实例, 最长可达50 轮, 比之前的最优区分器[44]长10 轮.对于MiMC, 得到的结果与Bouvier 等人[47]所证明的精确代数次数相一致.

2.3 Ciminion 和HYDRA

流密码算法Ciminion 的设计目标是最大限度地减少有限域F2n或Fp上的域乘法次数[5].在MiMC、GMiMC 和HADESMiMC 中, 非线性层均采用的是幂函数来对独立的域元素进行操作.而Ciminion 提供了一种不同的设计方法, 它的设计基于Toffoli 门[48]和一个简单的非线性双射, 将三元组(a,b,c) 转换为三元组(a,b,ab+c).同时, 为了进一步地优化实现性能, Ciminion 使用非常轻量级的线性层.由于作者最终的设计目标不是构造一个低乘法复杂度的密码, 而是提供一个低乘法复杂度的加密函数.因此, 他们通过采用Farfalle 结构[49]的修改版本来实现, 从而可以执行流加密.Farfalle 是一个有效的并行置换结构, 具有可变输入和输出长度的伪随机函数.采用Farfalle 结构的优点是可以尽量减少密码的轮数, 从而最大程度地减少域乘法的数量.设计者根据数据量限制条件分别定义了Ciminion 算法的标准实例、MPC应用实例及保守实例.为了促进对Ciminion 算法的进一步分析, 设计者还提出了Ciminion 算法的简化版本, 称为Aiminion 算法[6].

与MiMC、HADESMiMC 和Rescue 等相比,Ciminion 在MPC 中实现了最佳性能.然而,Ciminion的安全性高度依赖于其子密钥的独立性,这是通过使用复杂的密钥编排来实现的.由于许多涉及对称PRF的MPC 用例依赖于秘密共享的对称密钥, 复杂的密钥编排也必须在MPC 中计算.因此, Ciminion 在这些用例中的性能显著降低.2023 年, Grassi 等解决了这个问题[7], 他们按照Ciminion 设计者介绍的方法提出了Farfalle 的修改版本—Megafono 设计, 旨在实现较小的乘法复杂度, 而无需任何密钥编排.按照这种策略, 进一步提出了PRF HYDRA, 它同时利用了Lai-Massey 结构和在其非线性层中命名为Amaryllises 的新型结构.Amaryllises 可以看作是Lai-Massey 的变体, 它允许进一步降低HYDRA 的乘法复杂度.由于Ciminion 的密钥编排乘法深度较大, 且参与方之间的通信量较大, 因此, Ciminion 只有在不需要计算密钥编排时才具有竞争力.总的来说, HYDRA 在低乘法复杂度、小通信、良好的普适性能以及合理的深度之间取得了很好的平衡, 使其成为大多数网络环境中MPC 的首选PRF.

在Ciminion 的设计文档中, Dobraunig 等对其进行了全面的安全分析, 研究了Ciminion 对线性密码分析、差分密码分析、高阶差分密码分析、插值攻击和Gröbner 基攻击的安全性.由于Ciminion 的结构新颖, 传统分析方法对其安全性分析效果并不好.除此之外, 对于Gröbner 基攻击, 他们研究的是Ciminion的一个弱化版本.2022 年, Bariant 等人[50]针对实际的Ciminion 来建立方程组, 且给出的Gröbner 基攻击的渐近复杂度为O(24rω), 而设计者给出的攻击复杂度为O(26rω), 其中r为轮数,ω为矩阵乘法的指数.Zhang 等人[51]提出了F2n上Ciminion 的高阶差分区分器及Fp上Ciminion 的积分区分器.通过对Ciminion 轮函数的研究, 给出了轮函数的弱随机数条件, 并在弱随机数条件下, 提出了对Aiminion 的子密钥恢复攻击.

3 适宜FHE 的对称密码算法

3.1 Kreyvium

流密码Kreyvium[8]具有与Trivium 相同的内部结构, 但允许更大的密钥比特(128 比特).与Trivium 唯一不同的是, Kreyvium 在288 比特的内部状态中增加了两个128 比特的寄存器, 分别与密钥和IV相对应, 目的是使过滤和转换函数都依赖于密钥和IV.Kreyvium 相对于Trivium 的主要优势在于, 它在与Trivium 具有相同的乘法深度情况下提供了128 比特的安全性(而不是80 比特), 并继承了相同的安全性参数.除了更高的安全级别, Kreyvium 的另一个优点是可能的IV 数量, 以及在同一密钥下可以加密的最大数据长度.在HE 方案的具体实现中, 与LowMC 相比, Trivium 和Kreyvium 具有出色的性能.

2017 年, Liu[52]提出了对基于非线性反馈移位寄存器(NFSR) 的密码系统的代数次数迭代估计的一般框架.在此基础上, 进一步提出了一种求代数次数上界的有效算法, 算法具有线性时间复杂度, 需要的内存可以忽略不计.之后, 将以上算法应用于Kreyvium, 并通过设置不同的输入变量来分析代数次数的各种上界.Kreyvium 的初始化轮数为1152, 当Kreyvium 以所有密钥和IV 比特作为输入变量时, 使生成的密钥流比特达到最大代数次数的初始化轮数至少为982.当以所有IV 比特作为输入变量时, 初始化轮数至少是862.通过该算法, 可以在立方测试器中使用任意大小的立方.该算法为Kreyvium 找到的最好的立方大小为61, 利用该立方可以得到Kreyvium 的872 轮零和区分器.

在文献[53] 中, Wang 等人利用超级多项式(superpoly) 的各种代数性质来改进基于可分性质的立方攻击.基于大小为102 的立方, 作者提出了891 轮Kreyvium 的密钥恢复攻击.2018 年, 一种利用线性化技术在立方攻击中测试非线性超级多项式的一般框架被提出[54].对于Kreyvium, 结果表明, 使用新框架找到二次超级多项式的概率是找到线性超级多项式的两倍.2020 年, Kesarwani 等人[55]将Liu[52]的代数次数估计方法与文献[56] 中的贪心算法结合起来, 提出了一种新的立方生成算法, 得到了Kreyvium 大小为56 的立方, 并给出了875 轮的零和区分器.

2018 年, Watanabe 等人[57]给出了Kreyvium 的条件差分密码分析.他们分别利用20 阶和25 阶的高阶条件差分特征获得了Kreyvium 的730 轮和899 轮区分器.之后, 作者又根据20 阶的高阶条件差分特征得到了Kreyvium 的736 轮密钥恢复攻击.在文献[58] 中, Roy 等人利用差分故障攻击(DFA)技术, 提出了对Kreyvium 的密钥恢复攻击.通过注入3 个错误和考虑450 多个密钥流比特, 可以恢复Kreyvium 的完整密钥.

3.2 FLIP 和FiLIP

2016 年, Méaux 等人介绍了一种新的流密码结构—滤波置换器(filter permutator, FP)[9].主要设计原则是将布尔函数应用于常量密钥寄存器的公共比特置换, 从而使流密码输出的布尔复杂度是恒定的.更准确地说, 在每个周期, 密钥寄存器被伪随机生成的置换打乱, 然后对打乱的密钥寄存器的输出应用非线性滤波函数.这种结构的主要优点是总是直接对密钥比特应用非线性滤波函数, 从而使得输出的噪声水平是恒定的.之后, 作者研究了滤波置换器中各组件的优化, 基于梳状结构设计了一个滤波函数, 并指定了一系列滤波置换器, 称为FLIP.除此之外, 还给出了流密码FLIP 的几个实例, 用于80 和128 比特安全性, 该算法的特点是密钥长度远大于安全界.与LowMC、Trivium 和Kreyvium 相比, FLIP 设计具有非常低的乘法深度, 这使得它们也适用于第二代FHE 方案.在HElib 的实现中, FLIP 实例在延迟和吞吐量的性能方面综合表现良好.

Duval 等人[59]利用FLIP 的结构弱点对FLIP 的安全性进行了分析.他们采用的是猜测确定攻击的一种变体技术: 猜测一些空密钥比特的位置, 而不是对密钥或内部状态比特的值进行假设.FLIP 流密码系列的两个特征表明使用猜测确定攻击可能是有效的: 首先是其固定的内部状态, 其次是其滤波函数的定义.更准确地说, 寄存器不进行更新意味着在任何时候猜测一个密钥或内部状态比特, 都会给出一个比特的信息.攻击的主要思想是: 首先猜测空密钥比特的位置, 由于滤波函数F高阶的单项式数量很少, 在有很多空密钥比特的情况下, 高阶单项式有很大的概率被抵消.然后, 收集关于未知密钥比特的低阶方程, 选取那些空密钥比特可以将次数大于等于3 的单项式消去的方程.最后, 使用线性化技术求解方程系统.将以上攻击应用于FLIP 的两个实例进行密钥恢复, 针对80 和128 比特的安全级别, 时间复杂度分别为254和268个基本操作.FLIP 系列流密码的最大问题在于其滤波函数, 一个可能的改进方向是使用含有更多高阶单项式的滤波函数.在文献[58] 中, Roy 等人提出了对FLIP 的密钥恢复攻击.如果密码的状态中有1 比特错误, 那么从9000 个正常和错误的密钥流比特中就可以恢复密钥.对于单比特故障, 需要为每530个可能的故障位置求解方程组, 以恢复正确的FLIP 密钥.

2019 年, Méaux 等利用FP 并根据FLIP 的最新进展提出了改进的滤波置换器(improved filter permutator, IFP)[10], 主要从两个方向进行改进.首先, IFP 利用扩展密钥寄存器, 因此密钥大小大于作为滤波器的布尔函数的输入, 这使得滤波器的输入随着密钥大小的增加而越来越接近均匀分布, 而对于FP 情况则不同.其次, IFP 使用了一个白化阶段.也就是说, 在发送到滤波器之前, 经过置换的密钥比特先和一个随机的公共值进行异或操作.之后, 作者给出了具体的实例FiLIPDSM, 与现有的FLIP 实例相比, 它们进一步降低了乘法复杂度.在HElib 的实现中, 对于80 比特安全级别, FLIP、FiLIPDSM、Rasta 和Agrasta 的噪声是大致相同的, FiLIPDSM在延迟方面的表现最佳.对于128 比特安全级别,FiLIP-1280 的密文噪声略微小于Agrasta 和FLIP, FiLIP-1216 的延迟优于FLIP.

3.3 Rasta 及其变体

(1) Rasta

Rasta 是由Dobraunig 等人提出的面向全同态加密的流密码[11].与基于线性反馈移位寄存器(LFSR) 的流密码完全不同, Rasta 更像一种分组密码.它的设计同时考虑如下两个度量标准: 每个加密比特的与门数量和电路的乘法深度.该算法采用类ASASA 结构来生成密钥流, 其中替换层是公开且固定的, 采用的是Keccak 中的χ变换.仿射层包括一个二进制矩阵操作和轮常量异或的置换, 均是由nonce 和计数器通过可扩展输出函数(extendable-output function, XOF) 派生的.因此, 允许在分析过程中将矩阵和轮常量看作随机生成的进行处理, 但限制条件是相同的nonce 和计数器总是会得到相同的矩阵和轮常量.敌手在Rasta 中永远无法在同一密钥下访问相同的类ASASA 置换, 这种设计方法的优点如下: 一是可以防止文献[60–62] 中提出的攻击, 二是由于XOF 不使用秘密信息, 其不会影响FHE 应用中与AND 门相关的评估.基于线性密码分析、差分密码分析等经典攻击方法及代数攻击的结果, 作者建议Rasta 的轮数选取为4–6 轮, 并且给出了80、128 及256 比特安全级别下的分组大小.除此之外, 从理论的角度来看, 更低轮数的Rasta 实例也很有趣, 因此, 还增加了2 轮和3 轮的参数.与Kreyvium 和LowMC 对比, 它们允许密钥大小与安全级别一样, 而Rasta 和FLIP 一样, 需要更长的密钥.Dobraunig等人证明了即使Rasta 的乘法深度很小时, 如在2–6 之间选取, 某些攻击也可能不存在.传统上, 线性操作的成本与非线性操作相比几乎可以忽略不计, 但在某些环境中, 异或操作的数量过多, 不可以被忽略.与LowMC 类似, Rasta 需要的异或操作远远多于FLIP 和Kreyvium, 因此在FHE 应用场景中的计算代价不可忽略.根据实现的性能比较, Rasta 的乘法深度选取4 到6 在实际中是更有用的.

Rasta 的密钥大小主要由得到的单项式最大数量的界和存在好的线性逼近的概率界决定.然而, 在对Rasta 的分析中, 实际的攻击远小于以上界.因此, 作者进一步提出了密钥大小与安全级别匹配的一种Rasta 变体Agrasta, 其密钥大小等于安全级别大小加一.因此, Agrasta 在80、128 及256 比特安全级别下的分组大小分别为81、129 和257, 轮数分别为4、4 和5 轮.

(2) Dasta

由于Rasta 依赖于一个伪随机函数来生成仿射层中的矩阵, 导致在Rasta 中生成每次加密的仿射层非常耗时.因此, Hebborn 和Leander 提出了Dasta[12], Rasta 中的线性层被可变比特置换和确定性线性变换所取代.这种方法有如下优点, 首先, 由于线性层是固定的, 因此可以优化它们的实现.其次, 更重要的是, 可以将Rasta 的基于随机的安全参数提升到固定线性层情况下的参数.除线性层的生成外,Dasta 在密钥大小和轮数的参数选取方面和Rasta 相同.在离线密钥流的生成时间方面, Dasta 比Rasta快200–400 倍.在HElib[63]中实现的FHE 环境下, 与Rasta 相比, Dasta 的运行时间减少了大约15%–20%.

(3) Masta

尽管Rasta 在FHE 的成本度量方面提供了良好的结果, 但有两个缺点限制了它的实际应用.一是Rasta 在二进制明文空间上操作, 而大多数HE 方案都是在特定类别的环上运行.二是Rasta 的仿射层需要生成大量的伪随机比特, 导致在客户端需要大量的计算成本.因此, Rasta 的又一变体算法Masta 被提出[13].与Rasta 类似, Masta 将密钥和一个nonce 作为输入, 并为每个计数器生成一个密钥流.Masta的结构和Rasta 很相似, Masta 通过交替应用仿射层和χ变换来计算其密钥流分组.但Masta 与Rasta相比有两个主要区别: Masta 在非二进制明文空间上使用模运算, 并且它通过有限域乘法定义仿射层, 使得仿射层使用较少的随机比特.通过这种方式, Masta 在BGV/BFV 下的HE 方案的传输框架中优于Rasta.实现表明, 在客户端吞吐量方面, Masta 比Rasta 快505–592 倍, 在服务器端要快4792–6986 倍.

(4) Fasta

2022 年, Cid 等提出了用于实现更快同态加密的流密码—Fasta[14].Fasta 可以被认为是Rasta 的变体, 同样在二进制明文空间上操作.它采用6 轮类ASASA 结构的轮函数来生成密钥流, 其中非线性层为χ变换, 仿射层是基于移位操作构造的, 其中参数是随机生成的.Fasta 使用特定选择的参数和线性层使得其在BGV 方案中能有效地实现, 特别是在HElib 中的实现.并且所选取的参数利用BGV 提供的并行性, 使得密文中的槽被打包以在评估非线性层时可以实现完全并行.Fasta 实例的参数选择保证了128比特安全性, 其不仅可以作为独立的对称密码, 也可以与它所应用的BGV 方案的特定实例串联使用.在Rasta 中, 线性层是由随机矩阵生成的, 导致填充效率很低.因此, 在进行同态计算时, Fasta 比相应的(修改过的) Rasta 实例快6 倍以上, 比原始Rasta 版本快25 倍.

在文献[64] 中, Dobraunig 等利用相关密钥高阶差分区分器在单个明文/密文对条件下对1、2、3、4轮的Agrasta 进行了密钥恢复攻击.结果表明, 1、2、3 轮Agrasta 的密钥恢复攻击快于蛮力攻击.2021年, Liu 等人[65]指出, Rasta 和Dasta 的设计者忽略了χ变换的一个重要性质.结合Rasta 和Dasta 的特殊结构, 这一性质直接导致了代数攻击的显著改进.特别是, 他们在理论上能够分析3 个完整Agrasta实例中的2 个.主要策略是构建由χn表示的n位χ操作的可利用方程, 并且这些方程都是通过首先研究较小n的χn得到的.之后, Liu 等人[66]又证明如果χn的逆χ−1n的显式公式已知, 则所有这些可利用的方程都将是显式的, 并且在设计时可以避免类似Rasta 密码的弱点.他们给出了一个非常简单的χ−1n公式, 并以严格的方式证明了它的正确性.基于此公式, 可以很容易地推导出类Rasta 密码的可利用方程的公式, 从而找到更多可利用的方程.

3.4 Pasta

2021 年, Dobraunig 等人提出了面向混合同态加密(hybrid homomorphic encryption, HHE) 优化的流密码Pasta[15].与Rasta 相比, Pasta 同样采用类ASASA 结构的轮函数来生成密钥流, 但其使用两种不同的S 盒层, 这样做的目的是尽可能减少轮数.前r −1 轮采用的S 盒设计灵感来自χ变换, 最后一轮采用幂函数构造的S 盒S(x) =x3.此外, Rasta 中的前馈操作被截断操作所取代, 这允许以更有效的方式防止中间相遇攻击, 但代价是使用更大的状态.Pasta 的线性层生成也比Rasta 简单得多, 其并不直接生成随机可逆矩阵, 而是通过选取随机元素来构造两个序列矩阵, 然后通过混合操作将这两个矩阵组合成一个随机可逆矩阵.

Pasta 对定义在Fp上的明文进行操作, 与之前提出的大多数定义在F2上的对称密码相比, 大大提高了性能.此外, Pasta 利用最先进的整数HE 密码系统(BFV 和BGV) 的结构来最小化HHE 中的解压缩延迟, 同时仍然保持较少的轮数和乘法深度.作者评估了Pasta 在SEAL 和HElib 中的性能, 并和LowMC、Rasta、Dasta、Agrasta、Kreyvium、FLIP 和Masta 等对称密码算法进行了比较.结果表明,在同态计算时间和噪声量方面, Pasta 在HHE 中优于其竞争对手.具体来说, 当应用于HElib 中的一个小用例时, Pasta 的速度是Agrasta 的82 倍, 后者是目前FHE 中最快的算法.而当应用于SEAL 中的一个更大用例时, Pasta 的速度是Masta 的6 倍.

3.5 Chaghri

分组密码Chaghri 以Vision 的设计为起点[16], 采用SPN 结构, 状态向量为解密轮数为8 轮, 每轮包括相同的两步, 每步由S 盒层、线性层和轮密钥加组成.其中S 盒层包括一个幂映射G(x)=x232+1和一个仿射变换B(x)=c1x23+c2,c1,c2为常量.线性层是一个3×3 的MDS 矩阵.密钥编排实际上是迭代地应用解密轮函数.在HElib 的实现中, Chaghri 实现了0.28 秒/比特的吞吐量, 在相同设置下比AES 快63%.

在Chaghri 被提出后不久, 其安全性就遭受到了攻击.2023 年, Liu 等人[67]提出了一种称为系数分组的方法来评估Chaghri 的代数次数, 结果发现其代数次数增长是线性的而非指数的.核心思想是通过用一个整数向量来描述每一个指数集合, 从而将研究指数的传播简化为研究向量的传播, 这种方法的效率来自于如下事实: 向量的传播是确定的, 可以在线性时间内计算, 且与轮数无关.利用MILP 解决了将整数向量转化为代数次数的问题.作者又利用上述方法对Chaghri 构造了一个时间和数据复杂度均为263的13 轮区分器, 并进行了13.5 轮密钥恢复攻击.特别是对8 轮Chaghri 进行了高阶差分攻击, 时间和数据复杂度为238.因此, 以上分析结果表明8 轮的Chaghri 是远远不够安全的.Chaghri 的漏洞在于其使用了稀疏仿射变换B(x), Liu 等人进一步给出了新的仿射变换B′(x) =c′1x+c′2x22+c′3x28+c′4来替换B(x), 可以实现几乎指数级的代数次数增长.

3.6 HERA 和Rubato

2021 年, Cho 等人提出了一种支持对加密数据进行近似计算的同态加密框架, 称为RtF 框架, 可以在没有显著的密文扩展或客户端计算过载的情况下对实数进行加密[17].作为框架中流密码的一个实例, 他们提出了流密码HERA.HERA 的主要特点是在生成密钥流的轮函数中, 它使用一个十分简单的随机密钥编排, 即将主密钥直接与XOF 的输出随机值进行乘积操作.HERA 的轮函数与AES 类似, 对4×4 的状态矩阵进行操作, 除最后一轮外, 其轮函数包括列混淆、行混淆、S 盒层及轮密钥异或操作.与使用随机线性层的FLIP 和Rasta 等密码相比, HERA 需要更少的随机比特数.在HElib 的实现中, 与LowMC、FLIP、Rasta、Dasta 和Masta 相比, HERA 在客户端和服务端的延迟和吞吐量表现均是最优的.

2022 年,Ha 等提出了一个带噪声的流密码系列,称为Rubato[18].作为近似同态加密框架中LWE 加密和传统对称加密的结合, 该算法采用一种新颖的设计策略将噪声引入到一个低代数次数的对称密码中,Rubato 不适合对精确数据进行加密, 因为服务器在加密后可能会丢失原始消息的一些信息.Rubato 采用和HERA 一样的随机密钥编排, 轮函数也类似.与现有的适宜HE 的密码相比, 这种策略可以使得密码的乘法复杂度显著降低, 但不会降低整体安全性.更准确地说, 给定一个中等大小的分组(16–64), Rubato具有较低的乘法深度(2–5) 和每个加密字的少量乘法数量(2.1–6.25), 代价是密文扩展略大(1.26–1.31).与RtF 框架内的HERA 相比, Rubato 在客户端和服务端的吞吐量分别提高了22.9% 和32.2%, 代价是密文扩展仅增加了1.6%.

3.7 Elisabeth

2022 年, Cosseron 等将FLIP 和FiLIP 使用的滤波置换器的设计方法推广到任意群上, 提出了面向混合同态加密的流密码族Elisabeth[19], 并给出了一个实例: Elisabeth-4.在TFHE 实现中, 与FiLIP 相比, Elisabeth-4 的数据开销显著减少, 每比特的速度提高了5–27.5 倍.

4 适宜ZK 的对称密码算法

4.1 Jarvis 和Friday

2018 年, Ashur 和Dhooghe 提出了分组密码Jarvis 及其衍生杂凑函数Friday[20], 均在有限域F2n上运算.Jarvis 和Friday 的设计理念是提高在ZK-STARKs 中使用时的时间、存储和通信成本的效率.Jarvis 的设计灵感来自Rijndael, 通过构造一个具有与Rijndael 相似性质的密码, 使用宽轨迹策略来证明其对差分和线性密码分析的安全性.但与Rijndael 在轮函数中使用多个S 盒不同, Jarvis 对整个状态应用单个非线性变换, 其本质上是使用一个大的n比特S 盒S(x) =x−1.在Jarvis 中, 通过组合单个可逆S 盒、仿射置换多项式和密钥异或来获得轮函数.Jarvis 的密钥编排与其轮函数类似, 主要的区别在于省略了仿射变换.作者给出了Jarvis 的四个实例, 安全级别分别为128、160、192 及256, 且等于密钥大小(分组大小).Friday 是一个基于Merkel-Damgård 结构的杂凑函数.在STARK 证明生成时间方面,Friday 据称比Pedersen 杂凑函数具有20 倍的优势, 比基于MiMC 的杂凑函数具有2.5 倍的优势[68].

在Jarvis 和Friday 提出后不久, Albrecht 等人[69]就提出了对Jarvis 和Friday 的Gröbner 基攻击, 即对Jarvis 的密钥恢复攻击和对Friday 的原像攻击.尽管Jarvis 仿射多项式的高次数可以防止一些代数攻击, 但轮函数的特定代数性质使得Jarvis 和Friday 都容易受到Gröbner 基攻击.结果表明, Jarvis和Friday 轮数的选择不足以提供足够的安全性.

4.2 Vision 和Rescue

2020 年, Aly 和Ashur 等人作为对Jarvis 和Friday 的安全性遭受破坏[69]的回应, 首先系统地给出了针对提高STARK 效率的Marvellous 设计策略的一般结构及设计原则, 旨在提供一种通用的框架可用于在采用算术运算的应用环境中设计安全高效的密码算法.本质上, Marvellous 设计是一个由(q,m,π,m,v,s) 参数化的SPN 结构,q,m,π,m,v,s分别代表有限域的阶、向量空间维数、S 盒、MDS矩阵、常量及安全级别.之后, Aly 等人基于Marvellous 设计提出了一个新的SNARK/STARK 友好杂凑函数系列, 为Vision 和Rescue[21].Vision 在有限域F2n上进行运算, 每一轮轮函数包括两步: 第一步包括S 盒S(x) =x−1, F2上线性化的4 次仿射多项式B, MDS 矩阵M和轮常量加, 第二步非常相似,但将B替换为B−1.Rescue 在素域Fp上进行运算, 轮函数和Vision 一样包括两步, 第一步包括S 盒S(x)−1=x1/α, MDS 矩阵M和轮常量加, 第二步中将S(x)−1替换为S(x)=xα,α=3 或5.分别在采用AIR 和R1CS 的ZK-STARKs 零知识证明系统和MPC 这三个不同应用场景中分析Vision 和Rescue的效率, 结果显示, Rescue 在AIR 系统中比Vision、POSEIDON、STARKAD 和GMiMCerf更有效.在R1CS 系统中, 大多数情况下POSEIDON 的表现优于其他算法.这一结果主要是由于安全界的差异导致的.在MPC 中, Rescue 的在线通信轮数总是优于其他算法, Vision 和POSEIDON 在乘法数量方面有竞争力, 出现以上结果的原因一方面在于安全界的不同, 另一方面是由于不同的优化策略.STARKAD 和POSEIDON 的优化策略是最小化乘法数量, 而Vision 和Rescue 的优化策略是最小化通信轮数(即电路深度).

高级密码协议几乎普遍偏爱素域, 因此, Rescue 得到了比Vision 更多的关注.除设计者外, 2020 年,Beyne 等人[70]研究了Rescue 针对线性密码分析、差分密码分析、乘法子群的传播及反弹攻击的安全性.结果表明, 并未发现任何对Rescue 的直接威胁.在文献[71] 中, Szepieniec 等人以优化实现性能为目标, 基于原始的Rescue 设计进行简化, 提出了杂凑函数Rescue-Prime.改动包括三部分: 简化轮常量的生成方式—采用随机轮常量; 将安全余量从100% 降低到50%; 颠倒每轮两步中S 盒的顺序.2021 年,以太坊基金专门发起了针对Rescue-Prime、Feistel-MiMC、POSEIDON 和Reinforced Concrete 这几种适宜ZK 的对称密码算法挑战赛[72].2022 年, Bariant 等人[50]提出了一种通用方法在代数攻击中可以删除描述SPN 结构中前两轮的所有方程, 前提是第一个操作是S 盒层而不是线性层, 并且S 盒是一个单项式.将以上通用方法与多变量根求解算法结合起来, 针对挑战赛中使用t= 2 和t= 3 (字的个数) 的Rescue-Prime, 成功进行了缩减轮的攻击.

4.3 POSEIDON 和STARKAD

Grassi 等人提出了杂凑函数POSEIDON[22]和STARKAD[23].POSEIDON 是在Fp上运算的杂凑函数族, 其采用Sponge 结构进行实例化, 且内部置换是基于HADES 结构设计的, 被称为POSEIDONπ.在具有部分S 盒层的轮函数中,非线性部分仅使用一个S 盒,目的是降低R1CS 或AET 的代价.S 盒采用幂映射xα,α可选取−1、3 或5,且设计者声称x5更适用于ZK 应用中最流行的两个素域.POSEIDONπ的线性层是由柯西矩阵生成的MDS 矩阵, 生成之后需要利用文献[73] 中的方法判断矩阵是否存在无限长不变/迭代子空间迹.杂凑函数STARKAD 和POSEIDON 的结构一样, 但STARKAD 的设计基于有限域F2n, 且S 盒仅使用x3.

2020 年, Beyne 等人[44]给出了POSEIDON 和STARKAD 内部置换的零和区分器及作为杂凑函数时的原像攻击.在2021 年的欧密会上, Keller 等人[74]显著提高了POSEIDON 的差分和线性密码分析的活跃S 盒数量的下界.之后对STARKAD 算法给出了一个不变子空间攻击.证明对于任何t(即每轮中字的数量) 可被4 整除的STARKAD 算法实例, 该算法允许一个维数较大的不变子空间通过任意数量的P-SPN 轮而不激活任何S 盒.除此之外, 对于STARKAD 算法各种参数的选择, 这个不变子空间可以用于对杂凑函数进行原像攻击, 破坏了其安全性声明, 因此, 后来作者只保留了POSEIDON.在以太坊基金针对POSEIDON[72]发起的挑战赛中, POSEIDON 的S 盒为3且字的个数为3.2022 年,Bariant 等人[50]将可以删除描述SPN 结构中前两轮的所有方程的通用方法与单变量根求解算法结合起来, 针对挑战赛中的POSEIDON 成功进行了代数攻击.

4.4 Reinforced Concrete

2022 年, 为支持查找表的证明系统, Barbara 等人提出了一种新的面向零知识证明和可验证计算的杂凑函数Reinforced Concrete (RC)[24], 且使用的是基于KZG 承诺或FRI 的Plookup 协议[75].Reinforced Concrete 的设计目标如下: 一是最小化ZK 电路中门的数量, 从而最小化证明创建时间, 二是最小化普通计算的时间和电路约束的数量.它有两个突出的优点: (1) 使用查找表比模块化归约在ZK 和普通计算中的速度都更快, 从而使基于递归证明的可验证计算协议更高效; (2) 安全性不再仅仅基于(高) 代数次数,而是基于更传统的类似AES 部件.RC 采用Sponge 结构,其内部置换的设计思路基于POSEIDON设计策略, 即由两种不同的轮函数组成: 用于防止统计攻击的外部轮数和用于防止代数攻击的内部轮数.RC 置换的轮函数采用7 轮的SP 结构,在素域Fp上进行运算且字的个数为3.S 盒为低次数的Bricks 和高次数的Bars, Bricks 是F3p上的一个5 次非线性置换, Bars 是F3p上三个函数复合定义的一个置换.线性层由3×3 的MDS 矩阵和轮常量异或组成.在普通实现中, 与POSEIDON、Rescue 和Rescue-Prime相比, RC 的速度更快, 同时电路门数量更少.具体性能表现取决于素域的选择, 当使用通用的素域时, 如在BLS12-381 或BN254 椭圆曲线的标量域中, RC 比POSEIDON 快5 倍, 比Rescue 快125 倍, 比Rescue-Prime 快110 倍.与作为基准测试的最快的传统杂凑函数Blake2s 比, RC 只比其慢了80%, 但所需门的数量不到其七分之一.虽然RC 算法在计算速度上更优, 但其通用性和可拓展性不如其他算法.由于其S 盒设计非常复杂, 因此利用查表实现S 盒, 这也要求零知识证明系统支持查表运算.

4.5 Anemoi

Anemoi 是由Bouvier 等提出的定义在F2n或Fp上的杂凑函数[25], 与其他适宜ZK 的杂凑函数相比, Anemoi 的主要特征如下: (1) 它的设计目标是在多个证明系统(例如Groth16、Plonk 等) 中均是高效的; (2) 它包含针对特定应用优化的专用功能; (3) 在性能方面具有竞争力.在设计方面, Anemoi 内部置换的设计利用了CCZ 等价和算术运算之间的关系, 轮函数的操作类似于SPN 结构, 作者提出了两种新的组件, 一种是名为Flystel 的新型S 盒, 基于蝴蝶结构(butterfly structure)[76]进行设计.另一种是压缩函数Jive, 用于构造高效的Merkle 树.Flystel 置换分为开-Flystel 置换和闭-Flystel 置换.对于状态大小为偶数的Anemoi, 其S 盒采用开-Flystel 置换, 且第一轮的前两个轮常量由定义给出, 其余轮常量由闭-Flystel 置换得到.线性层可以分为两个子层, 其划分依据是零知识证明协议的不同.具体来说, 当零知识证明系统基于Plonk 时, 应当尽可能地减少加法运算的次数, 此时应采用Duval 和Leurent 提出的最低加法个数的矩阵[77].若采用ZK-STARKs 系统, 则应使用MDS 矩阵.线性层的第二层是伪Hadamard变换, 主要用于抵抗代数攻击.在R1CS 系统中, Anemoi 比POSEIDON 和Rescue-Prime 的效率高约2倍.在Plonk 约束下, 比POSEIDON 实现提高了10%–28%.

4.6 GRIFFIN

2022 年, Grassi 等提出了一种新的结构—Horst 结构[26].Horst 结构是将Feistel 结构中加法操作替换为乘法操作, 且保留原有的加法操作, 破坏了Feistel 结构原有的可逆性, 因此需要特殊函数G来保持Horst 结构的可逆性, 即(x,y)(y+F(x),x) 变为(x,y(y×G(x)+F(x),x).之后, 作者基于Horst 结构设计了一个新的杂凑函数族, 称为GRIFFIN, 其内部置换为定义在Fp上的GRIFFIN-π.GRIFFIN-π的轮函数采用SPN 结构, 但其非线性层和线性层与之前的设计不同.非线性层利用了Horst 结构, 并不采用独立S 盒的级联, 而是由三个不同的非线性函数定义的两个非线性子层组成的.根据状态大小可将线性层分为两种.当状态大小t= 3,4 时, 选择MDS 矩阵作为线性层.当状态大小t= 4t′≥8 时, 线性层可以定义为两个矩阵的乘积, 不仅可以在1 轮后就达到全扩散, 并且通过少量加法就可以实现.在实现方面, 主要与POSEIDON、Rescue-Prime 和GMiMCerf进行比较.在普通实现中, 当字的个数小于等于16时, GMiMCerf速度最快, GRIFFIN 的速度快于Rescue-Prime, 当字的个数大于16 时, GRIFFIN 的速度最快.在R1CS 系统中, GRIFFIN 需要最小数量的R1CS 约束, 且具有最快的证明时间.

5 总结与展望

云计算、大数据、物联网等新型应用的安全需求, 促进了安全多方计算、全同态加密和零知识证明等安全协议的发展和应用, 带动了新形态对称密码算法的设计与分析.自LowMC 被提出以后, 短短几年时间, 国际上公开发布了30 多个与相关应用相匹配的新形态对称密码算法, 发表了几十篇新形态对称密码算法的设计与分析论文.

新形态对称密码算法类型包括分组密码、流密码和杂凑函数.6 个分组密码算法中, LowMC 采用P-SPN 结构, HADESMiMC 采用HADES 结构, Chaghri 和Jarvis 采用SPN 结构, MiMC 的两种参数分别使用了SP 结构和Feistel 结构, GMiMC 使用了Feistel 类结构.除了LowMC, 其他5 个算法的非线性层均使用有限域上的幂函数, 其中MiMC、GMiMC 和HADESMiMC 都使用了立方函数.Jarvis 的轮变换由可逆函数、仿射置换多项式和密钥异或组成.虽然设计者声称设计灵感来源于AES, 但是整个状态用一个S 盒, 和宽轨迹策略没有关系, 该算法设计的重点是仿射置换多项式, 一方面为了安全性, 仿射置换多项式的次数要高, 项数要稠密, 保障轮函数的多项式表达式足够复杂.另一方面, 为了适宜STARK实现, 仿射置换多项式的次数或者其逆多项式的次数要尽可能小.LowMC 的设计亮点在于结构P-SPN,同时为了安全性要求, 线性层使用伪随机生成的二元可逆矩阵.15 个流密码算法中, Ciminion、Aiminion和HYDRA 都采用了Farfalle 类结构, FLIP、FiLIP 和Elisabeth 采用了滤波置换器, Rasta 以及变体采用类ASASA 结构, Kreyvium 具有和Trivium 类似的结构, HERA 和Rubato 都是针对RtF 框架设计的适宜FHE 加密的流密码算法.非线性层多使用二次或三次等低次函数, 同时希望非线性层的逆函数具有高代数次数.线性层多采用随机生成的线性变换或者随机数, 因此, 一般需要一个随机数生成器或者XOF 函数.比如FLIP 采用基于AES-128 的一种随机数生成器, 产生每一拍的随机置换.Rasta 及其变体、HERA 和Rubato 都利用基于杂凑函数的XOF 函数生成随机数或者随机线性变换.10 个杂凑函数,MiMCHash、GMiMCHash、POSEIDON、STARKAD、Reinforced Concrete、Anemoi 和GRIFFIN 算法都采用了Sponge 结构, Vision 和Rescue 采用参数化的SP 结构, Friday 采用MD 结构.MiMCHash和GMiMCHash 的内部置换来源于分组密码MiMC 和GMiMC, POSEIDON 和STARKAD 的内部置换采用HADES 结构, POSEIDON 面向素域, S 盒采用5 次幂函数, STARKAD 面向二元扩域, S 盒采用3 次幂函数.GRIFFIN 的内部置换结合了Fluid-SPN 和扩展Horst 结构, Horst 结构是GRIFFIN 的亮点.Anemoi 内部置换的非线性部件采用Flystel 结构设计, 其中用到了平方和立方等幂函数.Vision 和Rescue 分别面向二元扩域和素域, S 盒采用逆函数和幂函数.Friday 是基于Jarvis 分组密码的HASH 函数, 压缩函数采用Miyaguchi-Preneel 结构.

总的来说, 新形态对称密码算法还处于起步阶段.许多算法的非线性层设计相对简单, 采用低次数的幂函数, 导致算法加密过程中的中间状态可能存在线性或低次的多项式关系, 从而更易受到代数类分析方法的攻击.比如针对Jarvis 的Gröbner 攻击、LowMC 的代数中间相遇攻击、Chaghri 的代数次数的分析.算法结构方面, 推出了P-SPN、HADES、FP、Farfalle 和Horst 结构等, 对于这些结构缺乏系统的安全性研究, 设计思路、构造方式、参数选取等不同层次上均缺乏全面的理论基础.不同于传统对称密码算法, 多数新形态对称密码算法定义在素域、整数环或者二元扩域上, 而且运算规模比较大; 其次, 由于非线性层相对简单, 新形态对称密码算法的线性层一般比较复杂, 而且部分算法采用了随机生成的线性层;另外, 新形态对称密码算法的应用场景比较特殊, 对于安全性分析的数据复杂度等有较强的限制.因此, 传统的密码分析技术难以应用, 目前还没有针对这类算法的系统分析方法.虽然统计类分析方法和代数攻击等方式在对一些算法的分析中发挥了作用, 但可以注意到, 当推出新算法时, 很难对所有类型的攻击做出令人信服的安全论证.因此, 研究如何将现有分析技术应用到此类算法, 以及如何根据算法独特的设计方式和结构特点提出新的分析方法, 都是目前亟需解决的问题.本文介绍了新形态对称密码算法的发展历程、设计目标和理念、算法特点及最新的安全性评估成果, 致力于吸引国内更多的学者参与其中, 推动我国在相关领域的研究发展.