基于格的伪随机函数研究综述*
李一鸣, 刘胜利
1.上海交通大学 计算机科学与工程系, 上海 200240
2.密码科学技术全国重点实验室, 北京 100878
1 前言
伪随机函数(pseudorandom function,PRF)的概念是由Goldreich、Goldwasser 和Micali 在文献[1]中首次提出的.伪随机函数F:K×X →Y是多项式时间可计算且具有伪随机特性的确定性函数, 其伪随机性要求: 对于均匀随机选取的密钥k$←−K, 函数F(k,·) 的计算结果与真随机函数的计算结果之间计算不可区分.我们称描述伪随机函数F的集合K、X和Y分别为伪随机函数的密钥空间、消息空间和输出空间, 本文中, 考虑X={0,1}ℓ是长度为ℓ的比特串集合.部分伪随机函数在计算时还需使用到公开参数及相应的公开参数生成算法.
作为密码学领域的基础原语之一, 伪随机函数有着非常广泛的应用.伪随机函数结合Feistel 结构可以构造伪随机置换.基本的对称密码机制, 如对称加密、消息认证和身份识别, 都可以基于伪随机函数简洁地实现[1,2].进一步地, 伪随机函数也可作为组件构造对称版本的代理重加密和可更新加密[3,4]等高级对称密码方案.在公钥密码领域, 伪随机函数被创造性地应用于构造基于身份的加密、基于属性的加密、支持任意电路的功能加密以及数字签名方案[5–9].在协议设计中, 伪随机函数常用作密钥导出函数, 从相对短的密钥中方便地派生出足够数量的高质量密钥.具有扩展功能(如可验证、水印) 的伪随机函数还可用于设计区块链协议、设计电子货币系统、提供版权保护和盗版追踪等[10–14].除应用于密码方案的设计外,伪随机函数还被用于证明计算复杂性理论以及学习理论的重要结论[15,16].
伪随机函数具有定义简洁、可扩展性强、应用广泛等良好特点, 自提出至今一直都是对称密码领域内的一项重要研究内容.理论上, 伪随机函数可以基于伪随机数生成器(pseudorandom generator, PRG) 通用构造[1,17], 进而基于单向函数构造.但是这一黑盒构造通常效率较低, 而且通过这一方法构造的伪随机函数方案固有串行结构, 很难在浅电路内实现(例如, 文献[8] 中的伪随机函数的输入若为n比特, 则其相应的电路深度就与n呈线性关系).一般而言, 串行PRF 无法在浅电路内实现并不影响其实用性, 但是如果PRF 可以在浅电路内并行实现, 就可以充分利用多处理单元, 以更少的计算时间得到计算结果.如果PRF 被集成在专门设计的硬件设备中, 浅电路并行实现这一特点将会在实际应用中发挥极大优势.此外,PRF 经常和全同态运算结合, 应用于一些复杂密码算法的设计中, 如文献[5–7], 在这种情况下如果PRF电路深度过大, 会导致全同态运算的噪声迅速累积, 影响全同态运算的效率, 进而降低所设计的密码算法的效率.因此, 从某些特定应用的角度考虑, 在保证安全性的前提下, 设计效率更高、并行性更好的伪随机函数方案有着非常重要的意义.
格理论起源于1611 年开普勒提出的关于三维空间中等半径小球最大堆积密度的猜想, 历经诸多数学家的深入研究不断发展成熟, 并于上世纪末被创造性地应用于密码领域.格上有很多问题, 如最短向量问题、最近向量问题等, 被证明是难以求解的, 而且被普遍认为具备抵抗量子攻击的特性, 这使得格困难问题广泛用于后量子密码方案的设计.在量子计算理论以及实现技术快速发展的今天, 基于大整数分解和离散对数求解等传统数论困难问题的密码系统的安全性正遭受严重威胁, 对于后量子密码算法研究的重要性和紧迫性更加凸显.在这一背景下, 对格密码的研究有其重要价值和意义.
基于格困难问题设计伪随机函数的研究正式开启于2012 年欧密会上Banerjee、Peikert 和Rosen 发表的研究成果[18].Banerjeer 等[18]基于容错学习(learning with errors, LWE) 这一格困难问题构造了多个可证明安全的伪随机函数方案.受启发于这一工作, 密码学家们基于格困难问题设计了诸多伪随机函数方案, 并围绕PRF 的安全性、效率以及并行性等方面进行了改进[3,8,19–24].此外, 基于格困难问题设计具备扩展功能的伪随机函数也取得了诸多成果, 如具有密钥同态性质的伪随机函数[3,20,23,25]、约束伪随机函数[26–32]、水印伪随机函数[33–36]、可验证伪随机函数[37–39]等.尽管如此, 对于格上伪随机函数的研究仍然存在发展和完善的空间, 无论是针对PRF 构造方案属性进行优化, 还是丰富其功能以及应用场景, 都有进一步研究的价值.
本文主要针对格上伪随机函数的研究现状进行综述, 剩余部分安排如下: 第2 节回顾伪随机函数设计中经常使用的通用构造方案; 第3 节回顾现有格上伪随机函数方案所依赖的底层安全假设(困难问题);第4 节梳理现有基于格困难问题设计的伪随机函数方案, 重点关注这些方案在降低底层安全假设强度以及提升并行性方面采用的技术以及取得的成果; 第5 节简单介绍基于格困难问题设计具备扩展功能的伪随机函数的研究进展; 最后, 第6 节总结全文.
2 伪随机函数的通用构造方法
本节介绍两种经典的伪随机函数通用构造方法: 一种是Goldreich、Goldwasser 和Micali[1]提出的基于伪随机数生成器的通用构造方法, 将其简记作GGM-PRF; 另一种是Naor 和Reingold[40]提出的基于伪随机合成器(pseudorandom synthesizer,SYN)的通用构造方法,将其简记作SYN-PRF.这两种通用构造方法各具优劣: GGM-PRF 对组件的要求低, 一般来说对密钥的需求量小, 但是并行性差; SYN-PRF具有更好的并行性, 但是往往对密钥的需求量大.前述两种通用构造方法在伪随机函数方案的设计中有很多应用, 如文献[8,18,22,23,41].
2.1 GGM-PRF 通用构造方法
GGM-PRF 的组件是倍长伪随机数生成器(length-doubling PRG, ld-PRG).我们称确定性函数G:{0,1}s →{0,1}y是伪随机数生成器, 如果y>s, 且对于均匀随机采样的种子s$←−{0,1}s, 函数计算结果G(s) 与其输出空间{0,1}y上的均匀随机采样之间计算不可区分.特别地, 如果y= 2s, 那么G是一个倍长伪随机数生成器.GGM-PRF 的构造非常简洁: 对于输入ℓ ∈N 比特长消息的GGM-PRF, 其运算包含ℓ轮串行的ld-PRG 组件调用; 根据GGM-PRF 输入消息的第i ∈{1,2,···,ℓ}个比特从第i轮ld-PRG 的运算结果中选择一半作为第i+1 轮ld-PRG 输入的种子; GGM-PRF 的密钥作为初始ld-PRG 的种子; 第ℓ轮ld-PRG 的运算结果即为GGM-PRF 的输出.更正式地, 给定倍长伪随机数生成器G:{0,1}s →{0,1}2s, GGM-PRFFGGM:{0,1}s×{0,1}ℓ →{0,1}s的定义如下:
其中密钥s ∈{0,1}s, 输入x=(x1,x2,···,xℓ)∈{0,1}ℓ; 对任意种子s ∈{0,1}s, 符号G0(s)∈{0,1}s和G1(s)∈{0,1}s分别表示G(s) 计算结果的左半部分和右半部分.图1 给出了一个输入3 比特长消息的GGM-PRF 构造示例.

图1 GGM-PRF 构造示例, 其中输入消息为x=(101)Figure 1 An example of GGM-PRF with the message x=(101)
GGM-PRF 具有串行结构, 其运算电路的深度至少是输入消息长度的线性函数, 因此GGM-PRF 的实例化方案一般在并行性上会稍显逊色.另一方面, GGM-PRF 对于密钥的需求较小, 其密钥规模是固定的, 并不会随输入消息长度的变化而变化.
2.2 SYN-PRF 通用构造方法
SYN-PRF 通用构造方法使用了一种更强的组件, 即伪随机合成器.我们称确定性函数S:D×D →D是伪随机合成器, 如果对任意参数u,v(u,v= poly(κ) 是安全参数κ ∈N 的多项式函数), 任意u个左输入(x1,x2,···,xu)∈Du以及v个右输入(y1,y2,···,yv)∈Dv,u×v个所有可能的函数计算结果si,j=S(xi,yj)∈D都是伪随机的.SYN-PRF 采用了一种递归的设计思路: 给定伪随机合成器S以及两个输入消息长度为t的独立的伪随机函数F0,F1, 可以构造输入消息长度为2t的伪随机函数F(x1,x2,···,x2t) =S(F0(x1,x2,···,xt),F1(xt+1,xt+2,···,x2t)); 当t= 1, 函数F可简单实例化为根据输入的单比特消息从两个独立均匀随机的密钥中选择一个输出.基于前述递归思路, SYN-PRFFSYN,ℓ:D2ℓ×{0,1}ℓ →D的正式定义如下:
其中,k0和k1分别表示密钥k的左半部分和右半部分,x0和x1分别表示消息x的左半部分和右半部分.图2 给出了一个输入8 比特长消息的SYN-PRF 构造示例.

图2 SYN-PRF 构造示例, 其中密钥为k =(k10,k11,··· ,k80,k81), 输入消息为x=(10001101)Figure 2 An example of SYN-PRF with the key k =(k10,k11,··· ,k80,k81) and the message x=(10001101)
由图可知, SYN-PRF 对应着一棵深度为log(ℓ) 的满二叉树, 具有很好的并行结构.设伪随机合成器S的运算电路深度为dS, 那么FSYN,ℓ的运算电路深度为log(ℓ)·dS.但是注意到, SYN-PRF 的密钥数量是其输入长度的两倍, 其对于密钥的需求量相较于GGM-PRF 往往会更大1对于SYN-PRF 密钥需求量大这一问题有一个简单的解决方案: 可以借助伪随机数生成器, 由一个短密钥生成足够数量的密钥供伪随机函数使用..
3 格上困难问题介绍
格理论起源于1611 年开普勒提出的关于三维空间中等半径小球最大堆积密度的猜想, 后经诸多数学家的深入研究, 格理论不断发展成熟, 并于上世纪末被创造性地应用于密码领域.格上的很多问题被证明是困难的, 且被普遍认为具备抵抗量子攻击的特性.目前, 在设计伪随机函数时使用最多的格困难问题是LWE 问题[42]以及LWE 问题的一个确定性变型—舍入学习[18](learning with rounding, LWR) 问题.舍入容错学习问题[23](learning with rounding and errors, LWRE)在伪随机函数方案的设计中也有使用.此外, 还有子空间LWE 问题[43]等, 可以应用于消息认证码的构造[44].本节将对前述格上伪随机函数方案设计中使用的底层困难问题进行介绍.
3.1 LWE 困难问题
2005 年, Regev 在文献[42] 中首次定义了LWE 问题, 并给出了最坏情况格上困难问题到LWE 问题的量子归约; 后续, 文献[45,46] 又给出了格困难问题到LWE 问题的经典归约.这些研究成果为基于LWE 困难问题设计的密码方案提供了可证明安全的保障.判定版本的LWEn,q,χ,m问题指的是输入均匀随机矩阵A ∈Zn×mq和向量v ∈Zmq, 判断v是通过v⊤=s⊤A+e⊤(modq) 计算得到的还是从Zmq上均匀随机采样得到的, 其中, 参数n,q,χ,m分别对应LWE 问题的维度、模数、噪声分布以及实例数,公开矩阵A$←−Zn×mq和秘密信息s$←−Znq是均匀随机采样的, 噪声向量e ←χm是按照噪声分布χ采样的.相对应的, 判定性LWEn,q,χ,m假设指的是对任意概率多项式时间(probabilistic polynomial time,PPT) 的敌手, LWEn,q,χ,m问题都是难解的.
求解LWE 问题的难度与LWE 问题的维度n、噪声分布χ以及模数q有着密切关系.当噪声分布χ是以σ为参数的离散高斯分布且时, 求解LWEn,q,χ,m问题的难度至少与量子求解任意n维格上的判定版本近似最短向量问题GapSVPγ或近似最短线性无关向量问题SIVPγ的难度相当, 其中近似参数γ ≈O(nq/σ)[42].根据相关文献[47–51], 目前能够在多项式时间内求解的GapSVPγ或者SIVPγ问题需要具有指数数量级的近似参数, 即γ= 2Θ(nloglogn/logn); 如果近似参数γ= poly(n) 是维度n的多项式函数, 那么求解这些问题需要2Θ(nlogn)数量级的时间或者2Θ(n)数量级的时间及空间; 更一般化地, 如果渐进参数γ= 2k, 求解这些问题大约需要2˜Θ(n/k)数量级的时间2符号˜Θ(·) 表示括号内省略了一些小量, 如logO(1)κ; 符号 ˜O(·) 定义类似..而且即便是应用量子算法, 求解这些问题的时间复杂度或空间复杂度也不会有很大提升[52].
除上述标准的定义方式外, LWE 问题还有一些特殊变种, 这些变种LWE 问题同样被证明是难解的.文献[53] 证明了秘密信息s可以采样自噪声分布(或其他一些小模数的分布); 文献[3] 证明了公开矩阵A可以采样自一些特殊分布, 即“Coset Sampleable” 分布(相应LWE 问题称为non-uniform LWE, 简记作NLWE); 文献[22] 证明了秘密信息s和噪声向量e可以采样自Zmp上的均匀随机分布,要求p< 2q且p=nω(1).给定Q= poly(κ) 为安全参数κ的多项式,Q重LWE 问题指的是区分(A,s⊤1A+e⊤1,s⊤2A+e⊤2,···,s⊤QA+e⊤Q) 和(A,u⊤1,u⊤2,···,u⊤Q), 其中秘密信息s1,s2,···,sQ是独立均匀随机选取的, 噪声向量e1,e2,···,eQ是按照噪声分布独立采样的.借助混合论证技术可以证明, 求解Q重LWE 问题至少与求解LWE 问题一样难, 只是在归约损失上需要增加一个Q因子.
3.2 LWR 困难问题
2012 年, Banerjee 等[18]提出了一个LWE 问题的确定性变型, 即LWR 问题.具体地, LWRn,q,p,m问题指的是输入均匀随机矩阵A ∈Zn×mq以及向量v ∈Zmp, 判断v是通过v⊤=⌊s⊤A⌋p计算得到的,还是从Zmp上均匀随机采样得到的.其中, 参数n,q,p,m分别对应LWR 问题的维度、模数、舍入参数以及实例数, 公开矩阵A$←−Zn×mq和秘密向量s$←−Znq是均匀随机采样得到的, 舍入函数⌊·⌋p: Zq →Zp将Zq上的元素x映射为Zp上的⌊xp/q⌋modp3舍入函数运算可以扩展到n 维向量空间上, 设x = (x1,x2,··· ,xn)⊤ ∈ Znq, 令⌊x⌋p := (⌊x1⌋p,⌊x2⌋p,··· ,⌊xn⌋p)⊤..相应地, LWRn,q,p,m假设指的是LWRn,q,p,m问题是难解的, 即分布(A,⌊s⊤A⌋p) 与分布(A,⌊u⊤⌋p) 之间计算不可区分, 其中u$←−Zmq是均匀随机采样得到的4特殊地, 当p 整除q 时, ⌊u⌋p 就是Zmp 上的均匀随机分布..
Banerjee 等给出了一个LWEn,q,χ,m到LWRn,q,p,m的简洁归约, 其思路为: (1) 当模数q和舍入参数p满足q ≥nω(1)σp(或q ≥2κσp) 时, 分布(A,⌊s⊤A⌋p) 与(A,⌊s⊤A+e⊤⌋p) 之间的统计距离为n−ω(1)(或2−O(κ)), 是可忽略的; (2) 由LWEn,q,χ,m假设可证明, 分布(A,⌊s⊤A+e⊤⌋p) 与(A,⌊u⊤⌋p)之间计算不可区分.基于前述归约可知求解LWR 问题至少与求解LWE 问题一样难, 进一步结合LWE问题的困难性可知求解LWR 问题是困难的.
注意到, 上述归约成立要求LWR 问题的模数q至少是超多项式规模的; 如果追求分布(A,⌊s⊤A⌋p)与(A,⌊s⊤A+e⊤⌋p)之间的统计距离是指数级小, 那么q需要是指数规模的.为了放松LWE 到LWR 的归约对于模数q规模的约束,密码学家们进行了诸多探索.在提前给定实例数m的条件下,文献[8,54–57]基于LWE 假设证明了具有多项式模数的LWR 问题的困难性.文献[58] 提出了一个LWR 问题的特殊变型, 并基于LWE 假设证明了具有任意实例数以及多项式模数的变种LWR 问题的困难性.文献[59] 证明了LWE 到LWR 归约的不可能结论: 如果LWE 假设成立, 那么不存在LWE 问题到具有任意实例数以及多项式模数的LWR 问题的逐点归约(即归约中LWE 问题实例独立映射到LWR 实例).
3.3 LWRE 困难问题
2020 年,Kim[23]通过将LWE 问题和LWR 问题“链接”起来,提出了LWRE 问题.除描述LWE 问题以及LWR 问题的参数n,m,q,χ,p外, LWRE 问题还涉及一个链接参数τ ∈N.LWRE 实例是通过串联τ层LWE 实例和LWR 实例来定义的: 对所有i ∈{1,2,···,τ},第i层计算ri ←⌊s⊤i A+e⊤i ⌋p ∈Zmp;第τ层的计算结果即为最终输出.其中, 公开矩阵A$←−Zn×mq和每层计算时使用的秘密信息si$←−Znq都是独立均匀随机采样的; 除初始计算时使用的噪声向量e0设置为全0 向量外, 噪声向量ei ←Dχ(ri−1)是以第i −1 层的计算结果ri−1为输入, 调用分布χ上的采样算法采样得到的.LWREn,q,p,χ,τ,m假设指的是LWRE 实例与Zmp上的均匀随机采样之间计算不可区分.
Kim[23]给出了一个LWE 到LWRE 的归约证明, 从而将求解LWRE 问题的困难性归结到求解格困难问题之上.更具体地, 假设χ是以σ为参数的离散高斯分布且p|q, 如果存在敌手A可以以ϵLWRE的优势解决LWREn,q,p,χ,τ,m问题, 那么存在归约算法B, 可以借助A的能力以ϵLWE的优势解决LWEn,q,χ,m问题, 且有:

3.4 环上LWE 困难问题
Lyubashevsky 等在文献[60] 中提出了环LWE (ring-LWE, RLWE) 的概念.环LWE 的描述与标准的LWE 基本一致, 只是实例(公开参数矩阵、秘密信息以及噪声向量) 采样自一些特殊的环, 典型的如度为n的分圆环.Lyubashevsky 等证明了求解环LWE 问题至少与量子求解任意理想格上的近似最短向量问题一样困难, 从而证明了环LWE 问题的困难性.与LWE 相比, 环LWE 具备更好的紧凑性: 一个环LWE 实例相当于n个LWE 实例.因此, 基于环LWE 设计的密码方案往往具备更好的参数规模以及效率.此外, 文献[18] 和[23] 也分别提出了环版本的LWR 问题以及LWRE 问题, 并基于环LWE 假设证明了它们的困难性.
4 基于格的伪随机函数
格上伪随机函数的研究起始于Banerjee 等发表在2012 年欧密会上的工作[18], 他们给出了三个基于格困难问题的伪随机函数方案.第一个方案是基于LWR 困难问题实例化倍长伪随机数发生器, 进而实例化GGM-PRF 通用构造得到的, 记作FBPR,GGM.结合Banerjee 等[18]给出的LWE 到LWR 的归约, 该方案可基于超多项式模数的LWE 假设证明安全.但是受限于GGM-PRF 固有的串行结构, 该方案的运行电路深度是其输入长度的线性函数.
Banerjee 等[18]的第二个方案是基于LWR 困难问题实例化伪随机合成器, 进而实例化SYN-PRF通用构造方案得到的, 记作FBPR,SYN.这一伪随机函数方案具有更好的并行性.Banerjee 等给出的伪随机合成器实例化为SBPR: Zn×nq×Zn×nq→Zn×np, 其中SBPR(A,S) =⌊A·S⌋p.该伪随机合成器的计算仅涉及矩阵乘法以及舍入函数运算, 可在NC1电路内实现.故而方案FBPR,SYN是NC2电路可实现的.但是FBPR,SYN对底层困难问题的模数q有很高的要求, 其存在所谓的“模数堆叠” (power of moduli) 问题.注意到, 在SYN-PRF 通用构造中, 伪随机合成器组件的输出空间应与其左、右输入空间一致, 但是SBPR并不满足这一点.Banerjee 等给出的解决方案是为每一层的伪随机合成器设置不同的参数q,p, 即第i层伪随机合成器的参数分别为qi和pi, 而且pi=qi−1.根据SYN-PRF 的安全性证明, 每一层伪随机合成器的参数需满足qi ≥κω(1)pi=κω(1)qi−1.如此一来, 最底层伪随机合成器对应的参数qlogℓ(ℓ=poly(κ)是输入消息的比特长度) 在经过logℓ层的堆叠后, 其规模大约为κω(logℓ).也就是说, 方案FBPR,SYN的安全性最终依赖于超多项式模数的LWE 问题.
Banerjee 等[18]的第三个伪随机函数方案是一个(密钥) 子集合乘积结构的直接构造, 记作FBPR,Dir.设FBPR,Dir的输入消息比特长度为ℓ= poly(κ), 方案运算最多需要进行ℓ次矩阵或向量乘法, 因此可在NC2电路内实现.特别地, 该方案的环版本理论上具有更好的并行性, 可以在NC1电路内实现.方案FBPR,Dir的安全性可基于LWE 假设直接证明, 但是要求LWE 的模数q是安全参数的超指数函数.
2013 年, Boneh 等[3]基于LWE 假设给出了首个标准模型下的具有(几乎) 密钥同态性质的伪随机函数方案, 记作FBLMR.该方案采用了(公开参数矩阵) 子集合乘积的构造方法, 可以在NC2电路内实现.方案可基于NLWE 假设, 进而基于LWE 假设证明安全, 但要求模数q=κκ是安全参数的超指数函数.
注意到, 前述伪随机函数方案都要求底层LWE 困难问题的模数q是超多项式甚至是指数大小.然而,底层LWE 问题的模数太大会带来一些弊端.一方面, 如前所述, LWE 问题的困难程度与其模数的规模密切相关: 当模数q= poly(κ) 为安全参数的多项式大小时(对应格困难问题的近似参数γ为多项式), 即使是量子算法求解这样的LWE 问题也要指数级的时间或空间; 当模数q的规模增大, 特别是增大到安全参数的指数数量级(近似参数γ为指数数量级), LWE 问题的求解难度就会大大降低.因此, 基于大模数LWE 问题设计的伪随机函数方案, 其安全性要建立在更强的安全假设之上.另一方面, 底层问题的规模还会影响顶层方案的效率, 一般来说, 伪随机函数方案的参数规模、时间复杂度、空间复杂度等都会与其底层困难问题的规模相关, 因此, 当底层LWE 问题模数变大, 伪随机函数的参数规模和效率也会随之变差.
为了降低底层LWE 问题的模数规模, 提升伪随机函数方案的安全性以及效率, 密码学家们开展了大量研究工作并取得了诸多成果.现有工作中, 降低模数规模使用的方法大致有: 改进SYN-PRF 通用构造方案, 以解决模数堆叠问题; 借助特殊结构, 如树形结构和链式结构降低模数规模; 改进LWE 到LWR 的归约结果; 使用消息空间扩展技术.
改进SYN-PRF 通用构造方案.文献[24,61] 提出了不同的方法来解决FBPR,SYN方案中存在的模数堆叠问题.Banerjee 在他的学位论文[61]中, 对方案FBPR,SYN中原伪随机合成器的设计进行了改进.他将原先方案中的方阵都变为了行列数不同的矩阵, 更具体地, 修改后的伪随机合成器定义为SBan:Zn×mq×Zn×mq→Zm×mp, 其中SBan(A,S) :=⌊A⊤·S⌋p, 且参数满足pm=qn.然后, 他在每层伪随机合成器之上增加了一个可有效计算的双射K: Zm×mp→Zn×mq, 从而实现了上、下层伪随机合成器之间输入和输出的对齐.改进后的方案, 记作FBan,SYN, 其模数q的规模可优化为κω(1).Li 等[24]则通过在SYN-PRF 中引入伪随机数发生器, 同时结合中国剩余定理来解决模数堆叠问题.
树形结构和链式结构.Banerjee 和Peikert[20]提出了一类具有树形结构的、具有密钥同态性质的伪随机函数构造方案, 我们将其称为BP-PRF.BP-PRF 可以看作文献[3] 中伪随机函数方案的扩展和推广:它们都是通过在伪随机函数的计算中插入一些“比特分解” 操作, 来避免安全证明中底层困难问题的噪声累积过快.而BP-PRF 支持(基于二叉树结构的)更精细化的“比特分解”嵌入模式,从而能支持更灵活的参数选择.根据文献[20], 任意一棵完全二叉树都可以对应构造一个BP-PRF.如文献[3]中的方案就对应着一种特殊的完全二叉树, 即树中所有的右孩子节点均为叶子节点(“Left-Spin” 完全二叉树).图3(a)和图3(b)分别给出了对应满二叉树以及对应“Left-Spin” 完全二叉树的BP-PRF 构造.

图3 BP-PRF 构造示例: 基于满二叉树的BP-PRF 方案(a); 基于“Left-Spin” 树的BP-PRF 方案(b)Figure 3 Examples of BP-PRF based on a full binary tree (a) and a left-spine tree (b)
BP-PRF[20]的模数规模以及并行性均取决于其对应的完全二叉树T的形状.模数q的规模主要由二叉树的左深度(left depth) 决定.左深度, 记作e(T), 即从根节点到任意叶子节点路径上左孩子节点的最大数目, 也称作扩张因子(expansion factor).更具体地,q应满足q ≈σ·p·|T|·(nlogq)e(T)·κω(1),其中,n,q,σ为底层LWE 困难问题的参数,|T| 表示T中叶子节点的数目(也是BP-PRF 的输入消息比特长度, 设|T| = poly(κ)).BP-PRF 方案的并行性由T的右深度(right depth) 决定.右深度, 记作s(T), 即从根节点到任意叶子节点路径上右孩子节点的最大数目, 也称作串行因子(sequentiality factor).更具体地, BP-PRF 方案的电路深度约为max{s(T),log(e(T))}·O(logκ).总的来说, 当e(T) 变小, 底层LWE 问题的模数规模也可随之变小; 当s(T) 变小, 方案的并行性一般会随之提升.给定BP-PRF 的输入消息长度(即|T|)、e(T) 的上限e以及s(T) 的上限s, 可以通过动态规划构造最优解的完全二叉树.特别地, 如果约束e=s, 那么最优解有e(T)≈s(T) = log4(|T|), 此时方案的模数规模为q ≈κω(logκ),电路深度为NC2.如果忽略并行性, 那么可以取e(T)=1,s(T)=|T|−1, 此时q ≈κω(1), 电路深度至少是|T| 的线性函数.

Kim[23]还将这种“链接” 的思路应用到已有的伪随机函数方案之上.通过串联文献[20] 中的方案,Kim 构造了新的伪随机函数方案, 记作FKim,BP.该方案的模数规模以及并行性与链接参数τ以及组件的扩张参数e(T) 和串行参数s(T) 相关: 一方面, 方案的安全性要求(2|T|σme(T)+1p/q)τ−1是可忽略量;另一方面, 方案的电路深度为τ·s(T)·log|T| (参数定义参考BP-PRF).令e(T) = 1,s(T) =O(|T|),τ= Θ(κ), 此时方案的模数可取q= 4|T|σm2p, 是安全参数的多项式函数; 方案具备指数安全性, 但是需要线性深度电路实现.
改进LWE 到LWR 的归约结果.Banerjee 等[18]基于LWE 假设证明了LWR 问题的困难性, 但是这一证明成立要求模数q至少是安全参数的超多项式大小.源于这一限制, 基于LWR 假设设计的伪随机函数方案, 其安全性都需要依赖于超多项式模数的LWE 假设.Alwen 等[54]提出了一种新的LWE 到LWR 问题的归约方法, 简单来说, 基于LWE 假设可以将LWR 实例从正常模式切换至损失模式(lossy mode), 损失模式下的LWR 实例不会泄露太多的秘密信息, 因此求解是困难的.这一归约证明对于模数q的要求可放松为q ≥nmσp, 当取n,m,σ,p= poly(κ), 模数q也是安全参数的多项式函数.需要注意的是, 为保证参数满足q ≥nmσp, LWR 的实例数m需要提前给定.
结合Alwen 等[54]的归约结果, GGM-PRF 实例化方案FBPR,GGM[18]可基于多项式模数的LWE 假设证明安全, 为方便区分, 本文将应用了Alwen 等[54]结论的方案记作FAKPW,GGM.注意, GGM-PRF 方案的安全性证明只需要给定实例数的LWR 假设成立, 因此可应用Alwen 等的结果.而其他基于LWR 的伪随机函数方案, 其安全性证明需要LWR 假设对任意多项式大小的实例数m均成立; 如果对这些方案应用Alwen 等的结果, 方案就只能实现受限的伪随机性, 即方案的参数与安全实验中敌手提交的问询次数相关.
Lai 等[8]进一步优化了文献[54] 中LWE 到LWR 的归约证明, 给出了一个n重LWE 问题到Q重LWR 问题的紧致归约证明.借助这一结果, 他们提出了基于多项式模数LWE 假设的具有几乎紧致安全性的GGM-PRF 实例化方案, 记作FLLW,GGM; 该方案也需要线性深度的电路实现.Li 等[24]通过引入具有灵活输出空间的伪随机数发生器以及扩展伪随机合成器(generalized SYN, gSYN), 提出了一个SYN-PRF 通用构造方案的变型, 见图4.他们基于LWR 假设给出了该通用构造方案的两个实例化方案,结合文献[54] 给出的LWE 到LWR 的归约结果, 得到了两个基于多项式模数LWE 假设的伪随机函数方案, 其分别可在NC3和NC2电路内实现.但是源于文献[54] 归约结果的局限性, 这两个实例化方案仅具有受限伪随机性.进一步地, Li 等在前述实例化基础上借助“on-the-fly” 转换[19]解决了安全性受限的问题, 同时提升了方案并行性.最终方案, 记作FLLHG, 可基于多项式模数的LWE 假设证明安全, 且可以在NC1+o(1)电路内实现.
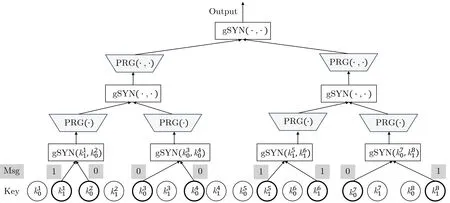
图4 FLLHG 构造示例, 其中密钥为k =(k10,k11,··· ,k80,k81), 输入消息为x=(10001101)Figure 4 An example of FLLHG, where the key k =(k10,k11,··· ,k80,k81) and the message x=(10001101)
使用消息空间扩展技术.一般来说, 伪随机函数方案的参数规模、安全性、效率和电路深度等都会与其输入消息的长度相关.基于这一思考, 一类伪随机函数的优化思路是, 先构造支持短输入的伪随机函数(这类伪随机函数往往可基于更弱的安全假设实现, 且效率和并行性更好), 然后再通过或串或并的方式由支持短输入的伪随机函数组合出支持正常输入的伪随机函数.简单地, 可以先借助通用哈希函数将伪随机函数的输入消息哈希为一个短输入, 然后再调用支持短输入的伪随机函数实现计算[62], 但是这一方案无法抵抗生日攻击.
Bellare 等[63]提出了级联(cascade) 的技术.级联技术使用支持单个消息的伪随机函数FBCK,1:K×X →K作为基本组件, 通过ℓ次串行调用FBCK,1, 得到一个支持ℓ个消息的伪随机函数FBCK,ℓ.级联技术构造思路如图5(a)所示.注意到, 上述级联构造要求组件FBCK,1的输出空间与其密钥空间一致,但对于基于LWR 假设或LWE 假设设计的伪随机函数方案来说, 很多都不满足这一点.Boneh 等[64]提出了增强级联技术(augmented cascade), 他们为每层单个消息的伪随机函数增加了一个外部输入的独立密钥, 去除了级联技术使用时要求输出空间与密钥空间一致这条限制.增强级联使用的基本组件为FBMR,1: (K×S)×X →K, 其构造思路如图5(b)所示.通过(增强) 级联的技术可以构造更高效的伪随机函数方案, 在某些实例化中还可以降低底层假设强度.
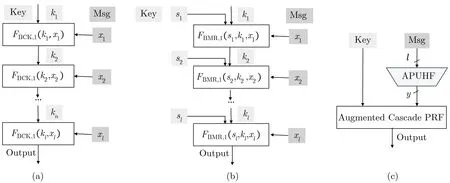
图5 级联技术(a)、增强级联技术(b) 和FJKP,Dir(c) 构造思路示例Figure 5 Illustrations of cascade technique (a), augmented cascade technique (b) and FJKP,Dir (c)
Jager 等[21]提出了一种增强的通用哈希函数, 即all-prefix 通用哈希函数(all-prefix universal hash function, APUHF), 其满足在任意位置对哈希函数的输出进行截断, 得到的新哈希函数仍然是通用哈希函数.Jager 等结合APUHF 以及增强级联伪随机函数提出了一个新的伪随机函数构造方法: 先调用APUHF 将伪随机函数的输入哈希为短向量(如将输入从ℓ= poly(κ) 比特长哈希到y=ω(logκ) 比特长), 然后再调用增强级联伪随机函数方案, 见图5(c).与增强级联方案相比, 该构造方案在效率、并行性、密钥规模以及归约紧致性上都有所提升.Jager 等给出了APUHF 的简洁构造, 并以伪随机函数方案FBPR,Dir[18]实例化了增强级联伪随机函数(FBPR,Dir可看作组件为F((S,a),x) =Sx·a的增强级联结构的伪随机函数), 由此得到了一个基于LWE 假设的伪随机函数方案, 记作FJKP,Dir.该方案具有几乎紧致的安全性, 其模数规模为q=κω(logκ), 且是NC1+o(1)电路可实现的.
Döttling 和Schröder[19]提出了另一种构造具有(几乎) 紧致安全性的伪随机函数的通用构造方法,其构造大致包含两个步骤.首先, 借助通用哈希函数将具有小消息空间的伪随机函数进行消息空间扩展,得到一个受限伪随机函数, 这里小消息空间指的是伪随机函数消息空间的规模为安全参数的多项式函数,对任意Q= poly(κ),Q-受限伪随机函数指的是对伪随机函数进行Q次不同的函数求值问询得到的结果是伪随机的.第二步使用了通用的归约技巧“on-the-fly” 转换, 由受限伪随机函数构造正常的伪随机函数.Döttling 等以FBPR,Dir[18]实例化了这一通用构造方案, 也得到了一个基于LWE 假设的伪随机函数方案,记作FDS,Dir.该方案具有几乎紧致安全性, 模数规模为q=κω(logκ), 且是NC1+o(1)电路可实现的.

表1 整理了现有格上伪随机函数方案的安全性(即敌手打破方案伪随机性的优势)、基于的底层LWE问题的模数规模以及方案的并行性.这些伪随机函数方案很多有其对应的基于环困难问题的版本, 这些环版本的方案与非环版本方案的构造方式一致, 但往往在方案的效率以及参数规模上有更好的表现; 部分方案, 如文献[18,22], 还在并行性上有所提升.对于环版本方案的结果, 表1 也进行了标注.

表1 基于格困难问题的伪随机函数方案Table 1 Lattice-based pseudorandom functions
5 基于格的扩展伪随机函数
除伪随机函数外, 密码学家们还不断地探索如何基于格困难问题设计具备额外功能的伪随机函数, 如具有密钥同态性质的伪随机函数、约束伪随机函数(constrained pseudorandom function,CPRF)、水印伪随机函数(watermarkable pseudorandom function, WPRF) 以及可验证伪随机函数(verifiable random function, VRF) 等.本节将对格上扩展伪随机函数的研究进展进行讨论.
5.1 具有密钥同态性质的伪随机函数
具有密钥同态性质的伪随机函数最早在文献[25]中提出,后续,Boneh 等[3]给出了它的正式定义.称伪随机函数F:K×{0,1}ℓ →{0,1}y具有密钥同态性质, 如果密钥空间及其上的运算(K,⊗)、输出空间及其上的运算({0,1}y,⊕) 构成群, 且对任意密钥k1,k2∈K以及消息x有F(k1⊗k2,x) =F(k1,x)⊕F(k2,x).有时会对这一定义进行放松, 称F具有γ-几乎密钥同态性质(γ-almost key homomorphic), 如果有F(k1⊗k2,x)=F(k1,x)⊕F(k2,x)⊕e, 且e ∈[0,γ]y.具有(几乎) 密钥同态性质的伪随机函数可以用于设计对称密钥版本的代理重加密以及可更新加密方案.前述文献[3,20,23] 中的伪随机函数方案都具有几乎密钥同态性.
5.2 约束伪随机函数/穿孔伪随机函数
约束伪随机函数的概念是由Boneh 和Waters[65]在2013 年提出的, Kiayias 等[66]和Boyle 等[67]也在同时期的独立工作中提出了类似的概念.约束伪随机函数允许通过约束函数来限制函数值的计算:CPRF 的主私钥msk 可以对约束函数f派生出密钥skf; 对于满足约束函数的输入, 即输入x满足f(x) = 1, 可以通过派生密钥计算函数值; 对于不满足约束函数的输入, 即使已知派生密钥, 其函数计算结果仍是伪随机的.穿孔伪随机函数(puncturable PRF, PPRF) 可以看作支持特殊约束函数的约束伪随机函数, PPRF 的约束函数是由某个点集S确定的, 即约束函数fS(x)=1 当且仅当x ∈S.
Brakerski 等[26]基于格困难问题设计了支持给定深度的电路族的约束伪随机函数, 该方案同时具有密钥同态性.Boneh 等[27]基于格困难问题设计了具有约束隐藏属性的穿孔伪随机函数.Canetti 等[28]及Chen 等[29]基于LWE 假设设计了支持NC1电路的具有约束隐藏属性的约束伪随机函数(constrainthiding CPRF, CHCPRF).Brakerski 等[30]以及Peikert 等[31]则分别基于LWE 假设设计了支持任意多项式规模电路的CHCPRF.Davidson 等[32]在标准模型下基于LWE 假设设计了一个支持内积函数的具有自适应安全性的约束伪随机函数.此外, 他们在标准模型下基于LWE 假设以及不可区分混淆(indistinguishability obfuscation, IO) 设计了一个支持P/Poly 电路的具有O(1)-抗合谋安全性的约束伪随机函数.
5.3 水印伪随机函数
水印技术允许在程序中嵌入一个“标记”, 同时不会影响程序的正常工作.其有两个基本的性质要求:一方面, 应当存在提取算法可以从嵌入水印的程序中将水印提取出来; 另一方面, 在不破坏程序功能的情况下将水印移除是很难实现的, 即水印不可移除.水印技术在数字版权保护方面有重要应用价值, 可以用于盗版追踪以及解决版权纠纷等.Kim 等[33]提出了首个基于格困难问题的水印伪随机函数方案, 该方案实现了一种弱的水印不可移除性, 即安全实验中不允许敌手询问水印提取预言机.后续, Quach 等[34]提出的基于格的水印伪随机函数实现了更强的水印不可移除性, 即使敌手访问了水印提取预言机, 仍然无法在不破坏伪随机函数功能的情况下移除水印.但是Quach 等的方案存在水印密钥权限过大的问题, 水印密钥的持有者可以破坏伪随机函数的伪随机性.Kim 等[35]基于LWE 问题分别在标准模型下和随机预言机模型下设计了具有强水印不可移除性的水印伪随机函数方案, 且(部分) 避免了水印密钥权限过大的问题.Kitagawa 等[36]首次考虑能够抵抗量子敌手的水印伪随机函数, 并给出了一个基于LWE 的支持秘密提取的WPRF 方案和一个基于LWE 和IO 的支持公开提取的WPRF 方案.
5.4 可验证伪随机函数
可验证伪随机函数是Micali 等[68]在1999 年提出的, 其允许对函数值进行公开验证, 同时不破坏函数计算结果的伪随机性.可验证伪随机函数与非交互式零知识(non-interactive zero-knowledge, NIZK)证明系统有密切联系, 且可以用于设计区块链协议、电子彩票和电子货币系统.目前大部分可验证伪随机函数方案[64,69–76]都是在配对群上的构造; 文献[77] 和[78] 同时期提出了一个可验证伪随机函数的通用构造方案, 使用了非交互式证据不可区分证明系统、承诺方案以及约束伪随机函数作为组件, 但是这一通用构造尚没有完全基于格困难问题的实例化方案.Chase 等[37]在公开参数模型下可验证伪随机函数的基础上增加了对于可模拟性的要求, 提出了可模拟的可验证伪随机函数(simulatable verifiable random function, sVRF), 给出了一个基于NIZK、承诺方案以及伪随机函数的sVRF 通用构造方案以及一个基于配对群的直接构造方案.Brunetta 等[38]尝试基于格假设对Chase 等提出的sVRF 通用构造进行实例化, 但是这一实例化并不完整(其中一个组件尚没有基于格困难问题的实例化).Li 等[39]提出了一个新的sVRF 通用构造方案, 并在标准模型下基于LWE 假设对这一通用构造进行了实例化.
6 结论
本文从伪随机函数的通用构造方案、设计伪随机函数常用的底层格困难问题、基于格的伪随机函数以及基于格的扩展伪随机函数这四个方面, 对格上伪随机函数的国内外研究现状进行了较为详细的总结.伪随机函数作为密码学领域的基础原语之一, 在对称密码和公钥密码方案设计以及解决现实问题上都有重要应用.作为底层组件, 伪随机函数的安全性以及效率将会直接影响顶层方案的安全性以及效率.因此如何设计安全、高效的伪随机函数方案一直都是密码领域备受关注的问题.格理论经历了30 多年的发展成熟,在同态加密以及其他高级密码方案的设计方面证明了其强大的能力; 此外, 格上的困难问题被普遍认为具备抵抗量子攻击的特性, 在后量子密码体制研究中亦处于关键地位.自然地, 如何基于格困难问题设计伪随机方案是一个很好的研究课题.从2012 年至今, 密码学家们在基于格困难问题设计伪随机函数方面取得了诸多成果, 尽管如此, 格上伪随机函数仍然有进一步发展和完善的空间, 无论是在方案安全性、效率或并行性上的提升, 还是丰富其功能以及应用场景等方面都有进一步研究的价值.本文给出一些值得进一步研究的方向供读者参考.
• 目前已有基于多项式模数LWE 假设且可以在NC1+o(1)电路内实现的伪随机函数方案[24]; 存在NC1电路可实现的PRF 方案, 但是依赖于指数规模模数的环LWE 假设[18,22].那么是否能设计PRF, 使其安全性能基于多项式模数LWE 假设, 且能在NC1电路内实现?
• 目前有许多方案对格上的伪随机函数进行了功能扩展, 如可模拟可验证伪随机函数, 支持多项式规模电路或抗合谋的约束伪随机函数, 具有不可移除性、不可伪造性、公开可嵌入或公开可提取性质的带水印的伪随机函数等.但是这些方案具有很高复杂度, 更多是提供理论上存在的证明, 距离实际应用还有一定差距.因此, 基于格设计具有扩展功能的伪随机函数, 如何避免使用类似非交互零知识证明、不可区分混淆或是多线性配对等复杂组件?如何在所依赖安全假设的强度、参数的规模以及方案效率上进行改进?这些都是很好的研究方向.此外, 随着(功能扩展) 伪随机函数应用场景的不断开发, 对现有(功能扩展) 伪随机函数又会不断提出新的功能、属性上的要求, 如何基于格困难问题设计伪随机函数变种以满足新的应用需求?这也是一个值得研究的问题.

