ARX 型密码算法的设计与分析*
孙思维, 胡 磊, 刘田雨, 牛钟锋, 汪达超, 张英杰
1.中国科学院大学 密码学院, 北京 100049
2.密码科学技术全国重点实验室, 北京 100878
3.中国科学院大学 网络空间安全学院, 北京 100049
4.隆德大学 电子信息系, 隆德
5.北京雁栖湖应用数学研究院, 北京 101408
6.清华大学 丘成桐数学科学中心, 北京 100084
1 引言
ARX 型密码是一类基于模加、(循环) 移位和异或等位运算构造的对称密码算法.由于现代微处理器对这些操作的原生支持, ARX 型密码的软件实现代码紧凑、效率高.另外, 由于模加可以同时提供扩散和混淆功能, 与使用S 盒作为非线性组件的对称密码相比, ARX 型密码避免了查表操作, 在一定程度上可以更好地抵抗基于时间的侧信道攻击.学界和工业界设计了一系列ARX 型对称密码, 包括分组密码、序列密码、密码学置换、杂凑函数、消息认证码和认证加密算法等.
ARX 型密码在实际中应用广泛.HIGHT 和LEA 都是ISO/IEC 国际标准分组密码算法.ChaCha20-Poly1305 序列密码在SSL 和TLS 安全协议中被广泛使用.ZUC-128[1]和SNOW 系列序列密码作为ISO/IEC 和3GPP LTE 算法标准, 被广泛应用于4G 通信领域.类Unix 软件包GNU 核心工具组的b2sum 命令实现了BLAKE2 杂凑函数.BLAKE2 在RAR 和7-Zip 压缩工具中应用于文件校验.SipHash算法被应用于网络流量验证和防御Hash-flooding 拒绝服务攻击等.Chaskey 作为ISO/IEC 的轻量级消息认证码标准, 被广泛应用在微处理器中.SM3 杂凑函数则是ISO/IEC 标准及中国国家标准, 在商用密码领域应用广泛.另一方面, 由于模加运算操作数的宽度一般为16 位、32 位或64 位等, 很难通过穷举的方式刻画其差分和线性等密码学性质.因此, 对ARX 型密码的分析往往比分析基于小型S 盒的设计更困难.本文对ARX 型密码算法的设计和分析进行了归纳总结, 并提出了多个ARX 型密码分析研究中亟待解决的开放问题.
2 代表性ARX 型对称密码
2.1 ARX 型分组密码
ARX 型分组密码包括FEAL[2]、RC5[3]、TEA、XTEA[4]、Bel-T[5]、HIGHT[6]、LEA[7]、SPECK[8]、SPARX[9]、CHAM[10]、Ballet[11]、CRAX[12]和TRAX[12]等.其中, FEAL[2]是第一个公开提出的ARX 型分组密码,对FEAL 的分析, 促进了差分分析和线性分析研究的发展.
FEAL分组密码.FEAL 是由Shimizu 和Miyaguchi 在1987 年提出的[2],与DES 相比,FEAL 更适用于软件实现.FEAL 的分组长度和密钥长度均为64 比特, 总轮数为8 轮, 其轮函数如图1 所示.FEAL 的加密过程见算法1, 记第i个轮函数(i ∈{0,1,···,7}) 的输入为(Li,Ri), 其中,Li=(L0i,L1i,L2i,L3i)∈(F82)4,Ri= (R0i,R1i,R2i,R3i)∈(F82)4.Kj= (K0j,K1j)∈(F82)2(j ∈{0,1,···,15}) 是由主密钥K ∈F642生成的, 具体生成方式见文献[2].

图1 FEAL 密码算法的第i 轮轮函数Figure 1 The i-th round function of FEAL
SPECK分组密码.SPECK 是由美国国家安全局Beaulieu 等人在2013 年提出的, 正式发表于DAC 2015[13].根据不同的分组长度和密钥长度, 该算法有十个版本, 每个版本的轮函数结构相同.分组长度为2n比特的SPECK 算法加密过程的第i轮如图2(左) 所示.密钥长度为mn比特的SPECK 算法的密钥编排如图2(右) 所示(其中Ri为图2 左图使用常数i作为轮密钥的轮函数).

图2 左: SPECK 密码算法的轮函数; 右: SPECK 密码算法的密钥编排算法Figure 2 Left: Round function of SPECK cipher; Right: Key schedule of SPECK cipher
LEA分组密码.LEA[7]是由Hong 等人在2013 年提出的, 目前是韩国标准分组密码之一.该密码算法有三个版本: LEA-128、LEA-192 和LEA-256, 分组长度均为128 比特, 密钥长度分别为128、192 和256).比特, 对应轮数分别为24、28 和32, 每个版本的加密过程使用相同的轮函数结构, 如图3 所示.LEA 采用了纯线性的密钥编排算法, 具体情况请参考文献[7].
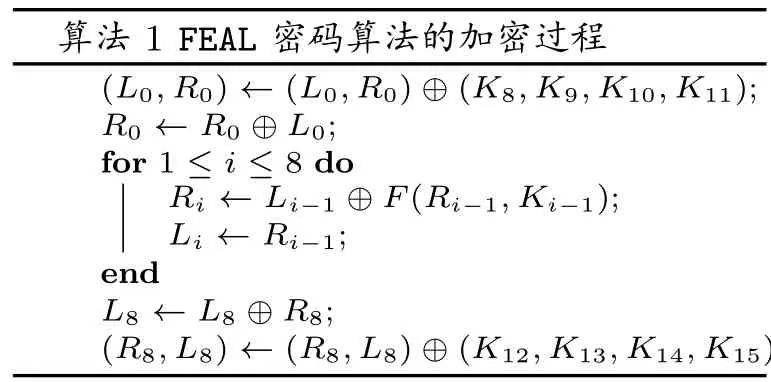
算法1 FEAL 密码算法的加密过程(L0,R0) ←(L0,R0)⊕(K8,K9,K10,K11);R0 ←R0 ⊕L0;for 1 ≤i ≤8 do Ri ←Li−1 ⊕F(Ri−1,Ki−1);Li ←Ri−1;end L8 ←L8 ⊕R8;(R8,L8) ←(R8,L8)⊕(K12,K13,K14,K15
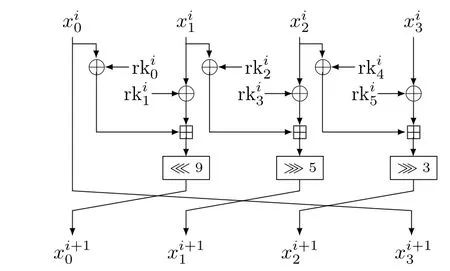
图3 LEA 密码算法的轮函数Figure 3 Round function of LEA cipher
Ballet 分组密码.Ballet 是由崔婷婷等人设计提出的, 是2019 年全国密码算法设计竞赛中获得一等奖的算法之一[11].该密码算法有三个版本: Ballet-128/128、Ballet-128/256 和Ballet-256/256,(Ballet-u/v的分组长度为u比特, 密钥长度为v比特) 轮数分别为46、48 和74.每个版本均使用相同的轮函数结构, 如图4 所示, 最后一轮省略最后一个线性置换操作.记分组长度为4n比特的Ballet 的第i轮轮函数的输入为(xi0,xi1,xi2,xi3)∈F4n2, (skLi,skRi)∈F2n2为第i轮的轮密钥.Ballet 使用了线性密钥编排算法, 细节见文献[11].

图4 Ballet 密码算法的轮函数Figure 4 Round function of Ballet cipher
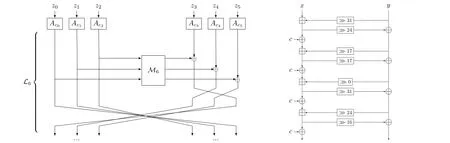
图5 左: SPARKLE 密码算法的第s 步; 右: SPARKLE 密码算法中的ARX-box Alzette (Ac)Figure 5 Left: The s-th step of SPARKLE cipher; Right: The ARX-box Alzette (Ac) in SPARKLE cipher
2.2 ARX 型密码学置换
密码学置换通常在其他对称密码中作为组件使用, 尤其是在基于海绵结构的杂凑函数和认证加密中经常使用.本节只介绍一个典型的ARX 型密码学置换SPARKLE[14].SPARKLE 是由Beierle 等人在2019 年提出的, 基于该置换构造的轻量级认证加密方案和杂凑函数参与了NIST 轻量级密码竞赛并进入第三轮.

2.3 ARX 型序列密码
典型的ARX 序列密码包括Salsa[15]和ChaCha.广义上讲, 在其算法中使用模加操作的对称密码都可以称为ARX 型密码.因此, SNOW 家族(包括SNOW[16]、SNOW 2.0[17]、SNOW 3G[18]和SNOW-V[19])和ZUC[20]等序列密码都可以被归类为ARX 型密码.
ChaCha 序列密码.ChaCha 是由 Bernstein 在 2008 年提出的, 是 eSTREAM 获胜算法Salsa20 的改进版本[21].ChaCha 的密钥流输出过程见算法2, 其中使用了一个所谓的1/4 轮函数QuarterRound(a,b,c,d), 如图6 所示.ChaCha 的初始输入可以看成一个4×4 的矩阵:

图6 ChaCha 密码算法的1/4 轮函数QuarterRound(a,b,c,d)Figure 6 QuarterRound(a,b,c,d), the 1/4 round-function of ChaCha
其中,ci为常数,ki为密钥,mi为nonce,ci,ki,mi的长度均为4 字节.

算法2 ChaCha 密码算法(x0,x1,x2,x3) ←(c0,c1,c2,c3); (x4,x5,··· ,x11) ←(k0,k1,··· ,k7);(x12,x13,x14,x15) ←(m0,m1,m2,m3); (y0,y1,··· ,y15) ←(x0,x1,··· ,x15);for 1 ≤i ≤r do if i is odd then QuarterRound(x0,x4,x8,x12); QuarterRound(x1,x5,x9,x13);QuarterRound(x2,x6,x10,x14); QuarterRound(x3,x7,x11,x15);else QuarterRound(x0,x5,x10,x15); QuarterRound(x1,x6,x11,x12);QuarterRound(x2,x7,x8,x13); QuarterRound(x3,x4,x9,x14);end end(x0,x1,··· ,x15) ←(x0,x1,··· ,x15)⊞(y0,y1,··· ,y15).
SNOW-V 序列密码.SNOW-V 是由Ekdahl 等人在2019 年提出的[19], SNOW-V 是为了满足5G 通信系统中的高速加密需求设计的, 可以视为SNOW-3G 的改进版本.SNOW-V 的内部状态(T0,T1,T2,T3,R1,R2,R3)∈F128×72按算法3 由线性反馈移位寄存器(LFSR) 和有限状态机(FSM) 进行更新.其初始化阶段及密钥流生成阶段分别如图7 和图8 所示, 其中两个AES 加密对应的轮函数的轮密钥设为零,σ为字节置换.在初始化阶段, FSM 的更新依赖于整个状态(T2,R1,R2,R3), 因此需要先执行FSM 的更新,再执行LFSR 的更新.SNOW-V 中LFSR 的更新如图9 所示, LFSR-A 与LFSR-B 满足

图7 SNOW-V 初始化阶段的轮函数Figure 7 Round function of initialization phase ofSNOW-V
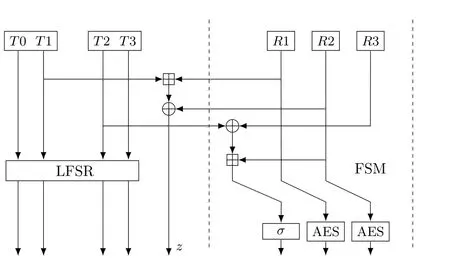
图8 SNOW-V 密码算法产生密钥流工作阶段的轮函数Figure 8 Round function of keystream generationphase of SNOW-V
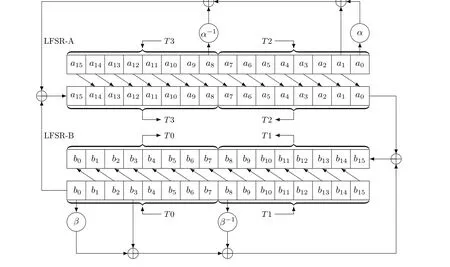
图9 SNOW-V 密码算法中的LFSRFigure 9 LFSR in SNOW-V
其中,α,β分别表示F2[x] 上两个不可约多项式gA(x),gB(x) 的根,α−1,β−1是相应域中的逆.gA(x) =x16+x15+x12+x11+x8+x3+x2+x+1,gB(x) =x16+x15+x14+x11+x8+x6+x5+x+1.若x ∈F216,x=(x15,x14,···,x0),在多项式gA(x)中αx=(x14,x13,···,x0,0)⊕x15·(100110010000111),(100110010000111) 为gA(x) 小于16 次幂的多项式系数; 多项式gB(x) 中同理.依次对LFSR-A 与LFSR-B 对应的等式进行8 轮计算,每一轮计算后将结果放在最高位a15,b15,原其他各位a15,···,1,b15,···,1向低位移动一位至a14,···,0,b14,···,0, 省略原最低位a0,b0.

算法3 SNOW-V 密码算法// 初始化阶段T3 = (a15,a14,··· ,a8) ←(k7,k6,··· ,k0);T2 = (a7,a6,··· ,a0) ←(iv7,iv6,··· ,iv0);T1 = (b15,b14,··· ,b8) ←(k15,k14,··· ,k8);T0 = (b7,b6,··· ,b0) ←(0,0,··· ,0);(R1,R2,R3) ←(0,0,0);for 1 ≤t ≤16 do z ←(R31 ⊞T31,R21 ⊞T21,R11 ⊞T11,R01 ⊞T01)⊕R2;FSM update();LFSR update();T3 ←T3 ⊕z;if t = 15 then R1 ←R1 ⊕(k7,k6,··· ,k0);end if t = 16 then R1 ←R1 ⊕(k15,k14,··· ,k8);end end// 产生密钥流工作阶段, 计算n 个密钥分组z while n > 0 do Output z ←(R31 ⊞T31,R21 ⊞T21,R11 ⊞T11,R01 ⊞T01)⊕R2;FSM update();LFSR update();n ←n −1 end
2.4 ARX 型杂凑函数
具有代表性的ARX 型杂凑函数包括SKEIN 家族[22]、BLAKE 家族[23]、ESCH[14]和我国商用密码标准算法SM3[24]等.
SKEIN 杂凑函数.SKEIN 是由Atighehchi 等人在2010 年提出的, 是SHA-3 竞赛中进入决赛的5个算法之一[25].SKEIN 采用了所谓的唯一分组迭代(unique block iteration, UBI) 结构和可调分组密码THREEFISH 构造.SKEIN 算法根据输出的摘要长度有三个版本, 分别为SKEIN-256、SKEIN-512 和SKEIN-1024.这里只介绍SKEIN-256.首先, SKEIN-256 中的可调分组密码THREEFISH-256 的密钥长度与分组长度均为256 比特, 调柄长度为128 比特.THREEFISH-256 共有72 轮, 每4 轮通过模加注入一次轮子密钥,其4 轮结构及其中的Mix 函数如图10 所示, 共Nr轮.Mix 是ARX 结构的函数, 其移位参数Rd,j与Mix 在THREEFISH-256 中的位置相关, 而Permute 是一个比特置换操作.令(k0,k1,k2,k3)∈F4×642 为主密钥,T= (t0,t1)∈F2×642 为调柄,k4= 0x1BD11BDAA9FC1A22⊕k0⊕k1⊕k2⊕k3,t2=t0⊕t1,Ks,i代表第s个子钥Subkeys的第i个字, 其计算过程如下:

图10 左: SKEIN 杂凑函数中THREEFISH-n 的前4 轮轮函数; 右: Mix 函数结构图Figure 10 Left: First four round functions of THREEFISH-n in SKEIN hash function; Right: Structure of Mix
SKEIN-256 的结构如图11 所示.其中, 初始链接值为256 比特的的全0 字符串, Config 为256 比特的配置字符串, 调柄值Ts= (first,final,Ttype,B,0119−log2len,len)∈F1282, 其中first、final、len 的值如图11 所示,Ttype∈{Tcfg,Tmsg,Tout}⊆F62,B ∈F2,B=1 表示分组的最后一个字节输入不足8 比特, 否则B=0.
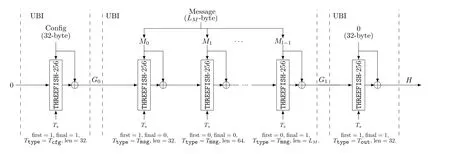
图11 SKEIN 杂凑函数结构图Figure 11 Structure of SKEIN hash function

图12 BLAKE2 杂凑函数的压缩函数Figure 12 Compress function of BLAKE2 hash function
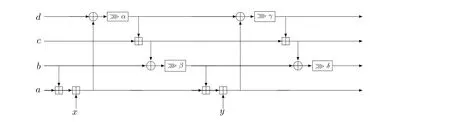
图13 BLAKE2 压缩函数Compress 中的函数G 的轮函数Figure 13 G function in compress function of BLAKE2
G函数的输入状态
然后对状态重复如下操作10 轮:

ESCH 杂凑函数.ESCH 是由Beierle 等人在2019 年基于海绵结构和SPARKLE 置换设计的杂凑函数[14], 该算法参与了NIST 轻量级密码竞赛并进入了第三轮.对于任意长度的消息, ESCH256 可以产生256 比特的杂凑值, ESCH384 可以产生384 比特的杂凑值.这里只介绍主要版本ESCH256, 其结构图如图14 所示.其中的SPARKLEnns为分组长度为n、步数为ns的SPARKLE 算法.在ESCH256 中, 基于的密码学置换为SPARKLE384, 函数Mhb的具体实例为M3, 如式(1)所定义.

图14 ESCH 杂凑函数结构图Figure 14 Structure of ESCH hash function
在ESCH 杂凑函数中, 需首先将消息M填充, 先补1 再补若干个0, 使填充后的消息长度为128 的倍数(若已满足此条件则无需填充), 并将消息分为长度为128 比特的消息分组, 记为P0,P1,···,Pℓ−1,ℓ为消息分组个数(如果消息为空, 则给P0填充至r比特).若最后一个消息分组有填充, 则记常数cM= (0,0,···,0,1)∈F1922, 否则记常数cM= (0,0,···,1,0)∈F1922.在消息吸收阶段, 初始状态为S=(0,0,···,0,0)∈F3842, 对于前ℓ −1 个SPARKLE 置换, 记为SPARKLE3847, 输入为S ⊕(P′j,0192), 即将P′j异或到状态的左半部分上, 其中P′j=M3(Pj||064),j=0,1,···,ℓ −2, 输出仍记为S.对于第ℓ个SPARKLE, 记为SPARKLE38411, 输入为S⊕(P′ℓ−1||0192)⊕cM, 其中P′ℓ−1=M3(Pℓ−1||064), 输出仍记为S.在挤出阶段, 截取状态S的左半部分128 比特, 记为D0; 在进行SPARKLE3847计算后, 截取状态S的左半部分128 比特, 记为D1最后的杂凑值即为(D0,D1).
SM3 杂凑函数.SM3 杂凑函数是2010 年公布的中国商用密码杂凑算法标准, 与SHA-256 等算法一样为Merkle–Damgård 结构, SM3 的安全性也与SHA-256 相当.首先, SM3 密码算法将消息长度填充至512的倍数, 在消息填充中, 需填充一个1, 再填充k个0, 其中k为满足(len+1+kmod 512=448) 的最小正整数, len 为消息长度比特.随后, 添加64 比特的数据长度len 的二进制表示.初始链接值IV∈F2562设置为0x7380166F 4914B2B9 172442D7 DA8A0600 A96F30BC 163138AA E38DEE4D B0FB0E4E; 压缩函数每次吸收一消息块m ∈F5122, 将链接值h= (A,B,C,D,E,F,G,H)∈F2562与消息块m作为输入, 压缩为h′∈F2562, 将h ⊕h′作为下一个消息块的链接值; 在吸收最后一个消息块后, 将更新的链接值作为杂凑函数的256 比特输出.SM3 密码算法的压缩函数为一个ARX 结构的迭代函数, 迭代轮数为64 轮, 如图15 所示, 其中, 压缩函数中的置换函数P0, 算法常量Tj ∈F322, 布尔函数FFj、GGj分别如式(2)–(5)所示.

图15 SM3 压缩函数结构图Figure 15 Structure of compress function of SM3
对于压缩函数的消息扩展算法,512 比特数据的消息块m划分为16 个32 比特消息字(W0,W1,···,W15),并以此16 个消息字生成另外的116 个消息字.消息字W16,W17,···,W67的生成过程为
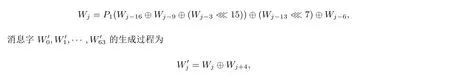
其中, 消息扩展中的置换函数P1(X)=X ⊕(X≪15)⊕(X≪23).
2.5 ARX 型消息认证码
ARX 型消息认证码(MAC) 通常基于ARX 型杂凑函数及密码学置换构造.杂凑函数可天然地构造MAC, 如基于BLAKE2 构造的MAC[27]和SipHash[28]等.其中, SipHash 由Aumasson 和Bernstein于2012 年设计, 是一族带密钥的哈希函数, 与HMAC 的构造方法类似, 设计时参考并结合了BLAKE 和SKEIN 等杂凑函数的特点, 其设计目的是为了应对2011 年底发生的一系列Hash-flooding 拒绝服务攻击.基于ARX 型密码学置换构造的MAC 如Chaskey[29]等.Chaskey 由Mouha 等于2014 年提出, 其置换的初始轮数为8 轮, 后改为12 轮, 12 轮版本的Chaskey 是ISO/IEC 轻量级消息认证码标准[30]之一.
Chaskey 消息认证码.Chaskey 消息验证码是由Mouha 等在2014 年设计提出的基于置换的消息验证码算法[29], Chaskey 密码算法中的置换函数π是基于ARX 结构设计的, 置换π的轮函数如图16 所示.
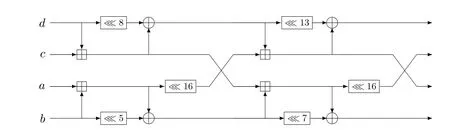
图16 Chaskey 密码算法中置换π 的轮函数Figure 16 Round function of permutation π in Chaskey cipher
Chaskey 密码算法如算法4 所示, 其中Subkeys(·) 将密钥K ∈F1282扩展为(K1,K2)∈F2×1282.其中,K1是由K扩展而来;K2是由K1扩展而来:
K ≪1 为将K左移1 位.
在计算第i个消息分组mi ∈F1282, 1≤i ≤ℓ −1, 置换π的输入为第i个π的输出hi与mi的异或(h1=K), 置换π对每个输入进行12 轮计算, 输出为hi+1.若最后一个消息分组mℓ的长度正好为128比特, 则令hℓ ⊕mℓ ⊕K1作为最后一个置换π的输入, 将输出结果与K1异或得到hℓ+1; 若最后一个消息分组的长度不足128 比特, 需先补1 再补若干个0 填充至128 比特, 并记为mℓ; 且将hℓ ⊕mℓ ⊕K2作为π的输入, 将置换π的输出与K2异或得到hℓ+1.最后, Chaskey 的输出MAC 值为hℓ+1的后t位.

算法4 Chaskey 密码算法(K1,K2) ←SubKeys(K); (m1||m2||···||ml) ←m; h1 ←K;for 1 ≤r ≤(l −1) do hi+1 ←π(hi ⊕mi);end if (|ml| = n) then L ←K1;else ml ←ml||10n−|ml|−1;L ←K2;end hl+1 ←π(hl ⊕ml ⊕L)⊕L;τ ←hl+1[n −t+1,n].
2.6 ARX 型认证加密
ARX 型带关联数据的认证加密方案(AEAD) 通常基于ARX 型序列密码和密码学置换等构造.基于ARX 型序列密码构造的AEAD, 如基于ChaCha20 构造的ChaCha20-Poly1305[31]和基于SNOW 3G和ZUC 构造的LTE 机密性和完整性方案[32,33]等.基于ARX 型密码学置换构造的AEAD, 如基于SPARKLE 构造的SCHWAEMM[14]等.
Schwaemm AEAD 认证加密.Schwaemm 关联数据的认证加密(AEAD) 是由Beierle 等人在2019 年基于SPARKLE 结构设计的密码算法[14], 其为一轻量级认证加密算法参与了NIST 轻量级密码竞赛并进入了第三轮, 对于给定密钥K、Nonce 值N、任意长度的关联数据A以及消息M(关联数据A与消息M的长度不要求相同), 输出一个与消息M等长的密文C以及一个固定长度的认证标签T.Schwaemm AEAD 的4 个版本对应的参数如表1 所示, 其中的SPARKLEnns为分组长度为n、步数为ns的SPARKLE算法, 以其主要版本Schwaemm256-128 进行介绍, 如图17 所示.

表1 Schwaemm AEAD 的参数设定Table 1 Parameters of Schwaemm AEAD
在Schwaemm256-128 AEAD 的加密过程中, 首先对关联数据A与消息M进行填充, 先补1 再补若干个0, 使填充后的关联数据A的长度与消息M的长度均为256 的倍数(若已满足此条件则无需填充), 并将其按256 比特分成若干分组.若A的最后一个分组有填充, 则常数ConstA ∈F3842设置为0x0⊕(0x1≪2), 否则设置为ConstA= (0x0)⊕(0x1≪2); 若M的最后一个分组有填充, 则ConstM ∈F3842设置为0x2⊕(0x1≪2), 否则设置为0x3⊕(0x1≪2).在初始化阶段, 其初始状态为(N,K), 经过SPARKLE38411, 输出为(SL,SR), 其中N,SL ∈F2562,K,SR ∈F1282.随后吸收ℓA个关联数据, 对于第j个关联数据, 0≤j ≤ℓA −2, 首先将(SL,SR)变换为(ρ1(SL,Aj)⊕W128,256(SR),SR), 其中W128,256(x,y)=(x,y,x,y),x,y ∈F642;ρ1(S,D)=FeistelSwap(S)⊕D,S,D ∈F2562; FeistelSwap(S)=(S2,S2⊕S1),S= (S1,S2),S1,S2∈F1282.随后进行SPARKLE3847运算, 输出为(SL,SR).对于第ℓA个关联数据, 首先要异或一个常量, 即SR=SR ⊕ConstA, 随后, 进行相似的运算, 但唯一不同点为使用的置换为SPARKLE38411.在加密阶段, 对于第j个消息, 0≤j ≤ℓM −1, 输出Cj=Mj ⊕SL作为密文.对于第j个消息的吸收, 0≤j ≤ℓM −2, 首先将(SL,SR) 变换为(ρ1(SL,Mj)⊕W128,256(SR),SR)运算, 其中W128,256(x,y) = (x,y,x,y),x,y ∈F642;ρ1(S,D) = FeistelSwap(S)⊕D,S,D ∈F2562;FeistelSwap(S) = (S2,S2⊕S1),S= (S1,S2),S1,S2∈F1282.接着进行SPARKLE3847运算, 输出为(SL,SR).对于第ℓM个消息的吸收, 首先要异或一个常量, 即SR=SR ⊕ConstM, 随后, 进行相似的运算, 输出密文CℓM并吸收消息MℓM; 但唯一不同点为使用的置换为SPARKLE38411.最后, 输出SR ⊕K作为认证标签T ∈F1282.
3 对ARX 型密码算法的分析
ARX 算法作为对称密码算法的一大子类, 针对基于S 盒设计的对称密码算法的分析方法也“自然”地适用于ARX 算法.在目前已知的密码分析中, 一般都是通过挖掘非线性部件的密码学性质, 来实现对整个加密算法的分析; 在基于S 盒设计的对称密码算法中, 由于非线性部件S 盒的规模较小, 可以采用枚举所有可能输入的方式来获取其密码学性质; 然而,在ARX 型密码算法中,由于其唯一的非线性运算—模加操作的规模比较大, 一般为32 比特的字, 枚举方式是不可行的, 相关的理论发展以及分析ARX 算法的工具往往是滞后的, 密码分析者需要去构建新的计算方法来挖掘模加操作的密码学性质进而实现对ARX算法的密码分析.本节将介绍模加操作在五种常用密码分析技术中的分析方法.这五种分析技术是: 差分分析、线性分析、差分-线性分析、可分性分析和飞来去器分析.为了明确模加操作中数值的比特长度, 本节使用符号“⊞” 来表示模2n的模加操作.
3.1 差分分析
差分分析是在1990 年由Shamir 等人提出的.在ARX 算法的差分分析中, 需要精确地刻画模加操作的差分概率: Prl,r∈Fn2[(l⊞r)⊕((l ⊕∆l)⊞(r ⊕∆r))=∆o], 记作(∆l,∆r)⊞−→∆o, 其中,l ∈Fn2,r ∈Fn2,(∆l,∆r)∈Fn2×Fn2是输入差分, ∆o ∈Fn2是输出差分.模加运算差分概率比特向量形式的快速计算方法最先由Lipmaa 和Moriai 在FSE 2001 上给出[34].2013, Schulte-Geers 通过CCZ 等价类的方法给出了相同的结果[35].之后, Wallén 等人给出了矩阵表达形式的计算公式[36].Mouha 等人从S-functions 的角度给出了相同的计算公式[37].Lipmaa 和Moriai 的计算方法在ARX 算法的差分分析以及自动化搜索中被广泛应用[38,39], 因而本节只介绍该计算方法.对于其他表达形式, 需参考相应的文献.最后, 在给出相关计算方法前, 首先给出模加运算与异或运算的关系:

结合模加的差分概率定义及上述定义, Lipmaa 等[34]给出了模加的差分概率计算方法.如定理1 和定理2 所述.
定理1 (∆l,∆r)⊞−→∆O非零的充分必要条件为:
(1) ∆l[0]⊕∆r[0]⊕∆o[0]=0;
(2) 对于任意i ∈[1,n −1], 若有∆l[i −1] = ∆r[i −1] = ∆o[i −1], 则∆l[i −1] = ∆r[i −1] =∆o[i −1]=∆l[i]⊕∆r[i]⊕∆o[i].
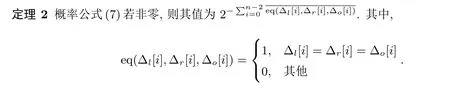
在实际使用中, 由于汉明重量的计算也可以使用位运算技巧将时间复杂度优化到O(logn), 故上述概率计算方法的复杂度可以优化到O(logn).
3.2 旋转差分分析
旋转差分分析是在ARX 算法分析中对差分分析的一种推广, 最早由Khovratovich 等人在FSE 2010上提出[40].在文献[40] 中, 对于ARX 算法E(x), Khovratovich 等人考虑了旋转不变概率, 即E(←−x)⊕←−E(x)= 0 成立的概率.类似于差分分析, Khovratovich 等人假定ARX 算法中的每个非线性操作(模加)均相互独立, 整个算法E(x) 的旋转不变概率等于每个模加旋转不变概率的乘积(旋转参数均一致).对于单个模加x⊞y, 在循环移位参数γ, 0≤γ ≤n −1 下的旋转不变概率定义为:

在FSE 2017 上, Ashur 等人给出了模加的旋转差分概率计算公式[42], 并成功应用到了轻量级分组密码算法SPECK 上.此外, 该公式类似于文献[34], 可以写成比特向量的形式; 模加的旋转差分概率计算公式的相关细节可以参考文献[42], 这里不做详细介绍.
3.3 线性分析
给定n比特的线性掩码Λl,Λr,Γ∈Fn2, 模加操作的线性逼近表达式为Γ·(l⊞r)⊕Λl·l ⊕Λr·r, 其中,l,r ∈Fn2.该线性逼近表达式的相关性定义为
记作cor⊞(Γ,Λl,Λr).
在2003 年, Wallén 给出公式(8)的快速计算方法[43], 解决了模加操作的线性分析中一大计算难题.之后, 在对SNOW 2.0 的分析中, Nyberg 和Wallén 又进一步给出更为通用的方法[44], 用于计算任意个加数的模加操作中的线性相关性.这两个研究工作中的线性分析理论都很长且复杂.这里不介绍过多理论细节, 只针对一个模加的情况, 简述得到的最终结论, 如定理3 所述.
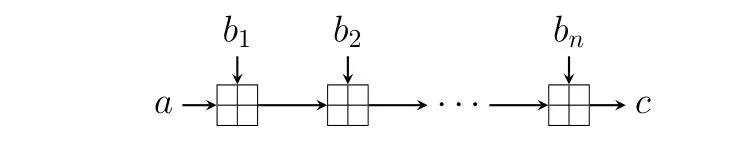
定理3 在cor⊞(Γ,Λl,Λr) 中, 用Λl[i] 表示掩码Λ∈Fn2的第i个比特, 对于Λr,Γ∈Fn2也有相同的记法.设向量u=(u[n−1],u[n−2],···,u[0])∈Zn8,其中,对于0≤i 推论1 公式(9)从左到右的计算过程对应于图18 中的有限状态自动机.状态转移箭头上的数字i代表当前要右乘的矩阵为Mi.如果自动机停机时的状态是“0”, 则线性相关性的计算结果为0.否则, 计算结果为±2−k, 其中k表示在图18 中标记为实线状态转移的转移次数.而正负号由{3,4}出现的次数决定, 出现偶数次则为正号, 反之为负号. 图18 模加操作的线性性质所对应的有限状态自动机Figure 18 Finite state automaton in linear cryptanalysis of a modular addition 此外, 关于模加的线性相关性计算, 也存在比特向量形式的计算方法, 该结果在2013 年由Schulte-Geers 通过CCZ 等价类的方法给出[35].具体理论可查阅相关文献. 差分-线性分析是将差分分析和线性分析结合起来的一类密码分析方法[45], 即通过短轮的差分区分器与线性区分器去构造长轮的区分器.其基本思想如下: 对于分组密码算法E=E2◦E1,E,E1,E2:Fn2→Fn2,假设E1存在差分概率为p的短轮差分区分器: ∆→δ(∆,δ ∈Fn2),E2存在线性偏差为ϵ的短轮线性 其中, ∆l,∆r,Λ∈Fn2.在文献[47] 中, 作者利用划分的方法, 成功解决了公式(10)的计算问题.这里只简单阐述其最终的计算方法, 如定理5 所述, 而具体的理论细节需参考文献[47]. 定理4 在公式(10)中, 用∆l[i] 表示输入差分∆l ∈Fn2的第i个比特.对于∆r,Λ∈Fn2也有相同的记法.设向量u=(u[n−1],u[n−2],···,u[0])∈Zn8,其中,对于0≤i 旋转差分分析是差分分析一“自然” 推广, 并成功应用到了ARX 算法的分析中[40–42,48].Liu 等人提出了利用旋转差分特征替换差分-线性攻击中标准差分特征的方法[49,50]; 并且作者考虑了线性逼近部分输出掩码为单比特向量的特殊情形, 给出了复杂度评估的方法, 将其应用到了Alzette、Siphash 这两个ARX 算法上; 并提出了输出掩码为任意情况时如何计算旋转差分-线性相关度的公开问题.即在数学形式上, 需要研究如下表达式的值. 其中, ∆l,∆r ∈Fn2, Λ∈Fn2为输出掩码. 随后, 在2022 年美密会上, Niu 等人解决了该公开问题[47], 他们基于计算单个模加差分-线性连接相关系数的方法, 将其进一步一般化, 给出了计算单个模加旋转差分-线性连接相关系数的方法.这里只简单阐述其最终的计算方法, 如定理5 所述, 而具体的理论细节需参考文献[47]. 定理5 在公式(12)中, 用∆l[i] 表示输入差分∆l ∈Fn2的第i个比特.对于∆r,Λ∈Fn2也有相同的记法.记γ为循环移位参数.设向量u= (u[n −1],u[n −2],···,u[0])∈Zn8, 其中, 对于0≤i 随后, Niu 等人基于上述理论, 给出了针对ARX 算法的(旋转) 差分-线性分析相关度评估的方法[47],并利用该方法对Alzette、Siphash、SPECK 和ChaCha 进行分析, 大幅度改进了已有的分析结果. 近几年, 针对ARX 的算法, 基于差分-线性区分器的最有效的密钥恢复技术之一为概率中立比特(PNB) 技术[51], 其主要思想如为: 对于R+r轮的密码算法, 假定有R轮的差分-线性区分器: ∆→λ.随机选取一对明文对满足差分∆, 进行加密, 假定在第R轮的中间结果为m,m′; 对于解密密钥的第i个比特, 若将其进行比特反转, 并对得到密文对进行解密r轮, 得中间结果n,n′; 如果λ·(m ⊕m′⊕n ⊕n′) = 0 的概率大于显著因子γ,那么解密密钥的第i个比特为R轮差分-线性区分器: ∆→λ的概率中立比特.对解密密钥的每一个比特逐一判定, 筛选出所有的概率中立比特.在恢复解密密钥的时候, 只需将概率中立比特设为定值; 对非概率中立比特位置, 进行猜测并解密r轮, 利用R轮差分-线性区分器进行密钥恢复.该密钥恢复技术通过后续的不断发展[52–57], 基于该技术的差分-线性分析得到了对ChaCha 算法与Salsa 算法最好的分析结果. 此外, 借鉴多重线性分析的思想, 利用“特殊” 的多条差分-线性区分器(基于“Partition” 技术[58], 即考虑输出在一特定集合上的线性逼近) 并结合额外的技术, 给出了目前对Chaskey 算法最有效的密钥恢复攻击, 详细细节见文献[52,59,60]. 可分性分析是由Todo 在2015 年提出的新的密码分析方法[61].该方法是对积分分析的扩展, 可以找到传统积分分析方法无法找到的区分器, 同时也推动了自动化积分分析技术的发展.这里参考文献[61,62], 先介绍可分性性质的定义.由于模加中采用的是比特级别的可分性分析, 这里着重于比特级别的可分性性质.对于任意两个n比特值k,k′∈Fn2, 若对于0≤i 定义2 设X 为一个多重集合, 其中的元素均为Fm2中的m比特值.当X 满足如下条件时, 称其具有 为了在模加操作中运用比特级别的可分性分析, 需要将输入值和输出值都表示为二进制形式.具体地,设模加操作的两个输入值为两个比特向量x ∈Fn2和y ∈Fn2, 输出结果为z ∈Fn2, 应用前文中的公式(6),并记c=carry0(x,y), 可以得到 (1)z0=x0⊕y0⊕c0,c0=0; (2) 对于1≤i ≤n −1, 有ci=(xi−1∧yi−1)⊕((xi−1⊕yi−1)∧ci−1) 和zi=xi ⊕yi ⊕ci. 最后, 运用上述可分性性质的三条规则, 可以得到模加的可分性性质的传播规则, 相关细节见文献[62]. 除了上述所介绍的可分性分析方法外, Todo 等人还提出可以进一步对公式(13)中的未知情况进行划分, 得到更为准确的可分性性质, 该性质称为“使用三子集的可分性性质”[63].文献[64] 中对模加操作的分析就采用了这个性质, 其规则与本节所介绍的分析规则是相似的, 但需要的规则会更多. 飞来去器分析的基本思想与差分-线性分析相似, 都是通过短轮区分器去构造长轮区分器, 唯一不同的是, 飞来去器分析的区分器是由两条短轮的差分区分器构造.相对其他的分析方法, 模加的飞来去器分析发展较为缓慢, 其主要原因是模加有关飞来去器的密码学性质尚未完全研究清楚.在飞来去器分析中, 密码算法E被拆分为三部分:E1◦Em ◦E0.其中, 对于E0和E1, 需要分别找到一条差分路径.对于Em部分, 需要分析两条差分路径(迹) 的连接情况, 本节只介绍Em为一个模加的情况. 此时, 模加的飞来去器分析就要求寻找图19 中飞来去器性质.该性质由如下概率表达式所描述. 图19 模加操作的飞来去器分析Figure 19 Boomerang cryptanalysis of a modular addition 该表的定义最早由Cid 等人给出[65].之后的研究工作[66–68]对该定义进一步完善, 并给出其快速计算方法, 其计算方式均为矩阵形式.但需要指出, 文献[68] 给出了一种通用的矩阵尺寸约简方法, 可以将矩阵大小约简至最优.因此, 这里以参考文献[68] 的结论进行简述. 设向量u= (u[n −1],u[n −2],···,u[0])∈Zn16, 其中u[i] 的值为8∆l[i]+4∆r[i]+2∇l[i]+∇r[i].那么, BCT 表中每一项的计算公式为 这个公式与线性相关性的计算公式在形式上是相似的, 但公式(9)中的矩阵存在很多相同的情况, 而这里的16 个矩阵都是完全不同的.这里不再一一列出, 它们的具体值参考文献[68] 给出的生成方法.同时, 在线性分析中, 8 个矩阵具有的特殊性质使得我们可以构建出图18, 从而简化计算以及进行自动化搜索建模.但在飞来去器分析中, 目前没有发现这16 个矩阵有类似的性质. 本节主要介绍了单个模加操作的分析技术, 但部分密码算法的分析会涉及到连续多个模加操作, 通常可简化为图20 的情形. 图20 连续的模加操作Figure 20 Consecutive modular additions 这种情况下, 通常有两种解决方法: 采用独立性假设对每一个模加操作进行单独分析, 再合并结果;将单个模加操作的计算公式推广到多个的情况.对于第一种方法, 由于独立性假设不一定总是成立, 最终结果与真实值存在一定差距.而在第二种方法中, 同时处理多个模加操作会增大分析的难度, 也会导致自动化模型过于复杂.目前, 这方面的研究工作较少, 主要集中于差分和线性分析.在差分分析中, 2010年Mouha 等人提出了S-functions 方法[37], 可以很自然地应用到任意多个模加操作的情况.同时, 针对SPECK, Dinur 还提出两轮密钥恢复技术[69].该技术应用到SPECK 的差分攻击中.关于旋转差分分析, Khovratovich 在文献[41] 讨论了多个模加操作的旋转不变性分析问题.在线性分析方面, Nyberg 和Wallén 将线性相关性计算推广到任意多个模加操作的情形[43,44].在差分-线性分析中, Beierle 等人在提出新的划分方法时也进一步考虑了连续两个模加操作的分析[52], 但相应的结果是通过采样实验得到的.在其他复杂的分析方法中, 如飞来去器分析, 目前还缺少相关工作, 其分析过程中主要采取独立性假设来简化研究. 针对ARX 密码的差分自动化分析方法最早是由Leurent 基于S-functions 实现的, 相应的软件工具为ARXtools[70].但该工具无法搜索最优差分路径, 仅对差分路径的验证效果较好.相比于Leurent 的建模方法, 后续发展起来的SAT 和MILP 建模方法更方便, 而且可以实现搜索与验证.因此, 这里仅介绍基于SAT 和MILP 的方法, 见文献[39,71].这两种方法的理论基础为定理1 和定理2. 在SAT 模型中, 由于第3.1 节中两个定理的表述以逻辑表达式为主, 因此可以很方便地将它们整理成如下的逻辑表达式, 即SAT 模型. 唯一的不同为差分概率值的表达.定理2 中的概率值为一个含幂指数的表达式, 该形式不利于构建SAT模型.因此, 取对数作为模型中的变量, 即 在SPECK 中, 根据独立性假设和堆积引理, 最终的目标函数就是所有模加运算的W值的总和, 通过设置约束W ≤k; 并将k由小到大尝试, 直至SAT 模型输出可行解, 即为搜索到的最优差分路径.对其他结构复杂的ARX 密码算法, 目标函数通常也是关于W的线性函数. 线性分析作为对称密码分析的另一种方法, 其自动化分析同样受到广泛的关注.与差分自动化分析不同, 推论1 中的有限自动机更适合MILP 建模.而对于SAT 建模, 需要寻找新的线性相关性计算方法.文献[73]从CCZ 等价角度得到的逻辑表达式,给出了适合SAT 建模的计算方法.本小节将简单介绍MILP建模和SAT 建模. 关于基于SAT 建模的自动化分析方法, 文献[73] 的方法涉及到CCZ 等价的知识, 这里不对细节进行描述, 只简述最终的SAT 模型.在线性分析中, 掩码Λl、Λr和Γ 需满足如下约束, 其中0≤i ≤n −1且0≤j ≤n −3. 在上述约束中, 由于异或运算可以转化为逻辑表达式输入到SAT 求解器中.但对于不等式的转化, 该文献采用了一种编码方法来解决这个问题, 这里只介绍结论.不等式∑i xi ≤k可以转化为如下逻辑表达式组, 其中1 至此, 结合上述逻辑表达式, 即可得到对应的SAT 模型. 差分-线性是对ARX 算法的比较有效的一类分析方法.然而,相比于差分分析与线性分析,ARX 算法的差分-线性自动化搜索发展缓慢, 仅在近几年有所发展.在CT-RSA 2023 上, Bellini 等人利用MQCP(混合二次约束规划) 对差分-线性的中间层Em进行建模[74], 首次实现了ARX 算法的差分-线性自动化分析.其建模过程如下.首先, 若已知各个比特上的差分分布, 且在各个比特上差分分布相互独立的情况下, 经过模加x⊞n y及异或x ⊕y后各个比特上的差分分布可以由以下定理计算. 定理6[49,75]令x,y,x′及y′为n比特串, 满足Pr[xi ̸=x′i]=pi及Pr[yi ̸=y′i]=qi.那么,x⊞n y上各个比特的差分分布为: Pr[(x⊞n y)i ̸=(x′⊞n y′)i]=pi+qi −2piqi −2pisi+4piqisi.其中,s0=0 且 在MQCP 模型中, 由于目标函数必须是线性函数; 但与差分分析以及线性分析相比, 差分-线性区分器的相关度并不是2 的整数次幂.因此, 为了用线性函数表示函数−log(|r|), Bellini 等人基于分段线性插值来逼近非线性函数的思想[74], 将区间分成若干段, 在每段区间上用线性插值, 将−log(|r|) 表示为: 对于差分部分与线性部分的建模, 采用前面提及的MILP 建模, 从而完成了对差分-线性搜索的MQCP 建模; Bellini 等人将该自动化方法应用到了SPECK 算法上[74], 找到了一系列可实践验证的差分-线性区分器, 且这些区分器都是目前最优的. 作为积分分析的扩展, 可分性的自动化分析在近几年受到广泛关注.因此, 成功实现对积分分析的自动化分析成为一个非常重要的问题.如第3.5 小节所述, 模加运算的可分性性质可由三条基本规则构成, 只需为这三条基本规则构建相应的MILP 模型和SAT 模型, 就可以组合出可分性的自动化分析模型.对于MILP 建模, 文献[76] 给出了三条基本规则的MILP 建模, 分别如下. 飞来去器分析虽然作为差分分析的扩展, 但是其在ARX 密码上的发展很缓慢.Leurent 在2013 年给出ARXtools 也同样适用于飞来去器分析[70], 但其只能验证区分器, 无法寻找新的区分器.之后, 直到2020 年, Kim 等人才给出中间层的概率计算公式[66].但该工作并未涉及ARX 密码的飞来去器自动化分析, 其采用的策略依然为先寻找差分路径再尝试进行两两拼接.在2023 年, 我国学者Wang 等人给出了第一个自动化分析方法[68].由于篇幅限制, 本小节仅简述其思路. 该方案采用的为SAT 建模.最大的问题为对公式(15)的建模, 但由于最终的结果不是2 的整数次幂,无法与差分分析一样取对数作为目标函数.文献[68] 通过分析矩阵的性质, 给出一个新的建模方法来避开该问题.在公式(15)中, 对于0≤i ≤n −2, 记 该研究工作将其应用到了SPECK 上, 成功找到目前SPECK 最好的飞来去器区分器.但对于ARX 密码的飞来去器自动化分析, 目前还缺乏足够的研究, 有待后续研究者去研究新的自动化方案. 在ARX 算法分析中, 目前仍然存在很多未解决的重要问题.首先, 在针对Chaskey、ChaCha、Salsa等算法的差分-线性攻击中, 使用了大量实验型差分-线性区分器[52–57,59,60].对这些区分器的相关度计算缺少理论方法.尽管目前有一些对ChaCha 差分-线性区分器相关度进行理论解释的尝试[78], 但相关方法不具一般性, 只对个别特殊情况有效.特别是对于Chaskey 算法的差分-线性区分器[52,59,60], 目前没有任何理论解释的工作. 第二, 对于基于ARX 型置换构造的密码方案, 虽然可以较为容易地搜索到这些密码方案底层置换的区分器(例如, 4 轮Alzette 存在相关度为1 的差分-线性区分器[47]), 但如何利用这些区分器构造上层方案更有意义的攻击(如原像攻击、碰撞攻击、密钥恢复攻击等) 也是非常值得关注的问题. 第三, 对于ARX 算法的可分性分析, 目前的方法还是首先将模加运算分解成比特级与运算和异或运算, 然后再根据可分性特征在这些基本运算中的传播规律去刻画可分性特征在整体模加运算中的传播特征.从单项式预测方法的角度看, 这种方法有可能忽略一些单项式的相消现象, 从而不能精确描述可分性特征在模加运算中的传播规则.另一方面, 尽管模加运算会导致较高的代数次数, 从而似乎可以更好地抵抗可分性分析.但有趣的是, 在基于长轨迹策略设计的SPARX 系列算法中, 基于可分性的密钥恢复攻击是目前最好的[9], 因此, 针对ARX 算法的可分性分析工作是值得进一步挖掘的. 最后, 关于ARX 算法的飞来去器分析, 与差分-线性分析相似, 都是通过覆盖较短轮数的显著的区分器去构造覆盖较长轮数的区分器.但相比于基于小型S 盒构造的对称密码算法[79–83], 针对于ARX 型密码的飞来去器分析工作进展缓慢.在基于S 盒构造的对称密码中, 由于S 盒的规模一般较小, 对其飞来去器的密码学性质, 可以通过遍历所有的输入来得到.此外, 在由S 盒构成的非线性层中, 每个S 盒都是独立的, 可以通过局部飞来去器密码性质推导出整体轮函数的飞来去器密码学性质.然而, 对于ARX 算法,由于模加运算的规模比较大, 通过遍历所有的输入来得到飞来去器密码学性质是不可行的.另外, 由于进位比特的影响, 使得模加当中的任意两个比特都有联系, 难以通过局部的规律得到整个轮函数的密码学性质.而从目前仅有的一些对ARX 算法的飞来去器分析工作来看[84,85], 针对ARX 算法的飞来去器分析工作值得进一步发展.

3.4 差分-线性分析



3.5 可分性分析

3.6 飞来去器分析


3.7 连续多个模加操作的分析
4 自动化分析
4.1 差分分析的自动化分析

4.2 线性分析的自动化分析

4.3 差分-线性的自动化分析

4.4 可分性的自动化分析

4.5 飞来去器的自动化分析

5 讨论与公开问题

