口令猜测研究进展*
邹云开, 汪 定
1.南开大学 网络空间安全学院, 天津 300350
2.天津市网络与数据安全技术重点实验室, 天津 300350
3.数据与智能系统安全教育部重点实验室, 天津 300350
1 引言
口令, 英文为“Password”, 坊间称为“密码”.口令是人类可记忆的短密钥, 是全球53 亿网民可感知、直接接触的密码学组件.口令最早由麻省理工学院的费尔南多·科尔巴托教授引入计算机领域, 用于大型计算机的本地文件访问控制[1].上世纪90 年代, 随着个人计算机和互联网的迅速发展, 各类服务不断上网,口令除了提供数据加密、数字签名等安全功能, 也成为使用最广泛的身份认证方式, 保护着用户绝大多数的数字资产.然而, 随着用户需要管理的网络账户数量的增加, 用户在创建口令时也面临着巨大的安全挑战.一方面, 人类的记忆力有限且长期保持稳定, 通常只能记忆5∼7 个不同口令[2]; 另一方面, 许多网站对口令的复杂度和长度提出了明确的要求(如网页托管服务公司000Webhost 要求用户创建的口令长度至少为6, 且至少包含一个数字和字母), 使得用户记忆众多账户的口令变得愈发困难.这导致许多用户为了方便记忆而采用简单易记的流行口令, 在不同账户中使用相同口令, 使用个人信息创建口令[3].这些脆弱行为一旦被攻击者利用, 将导致严重的安全隐患.
自2000 年以来, 数以千计的各种各样新型身份认证方案被提出, 如多因素认证[4]、生物识别技术[5]以及硬件安全密钥[6]等, 但这些方案在可用性、安全性和隐私保护等方面往往没有取得平衡[7,8].同时,它们在可部署性上也常常劣于传统的口令认证[9].因此, 自2012 年以来, 学术界逐渐达成共识[8,10–12]:在可预见的未来, 口令仍将是最主要的身份认证方法, 基于口令的认证技术仍无可替代.
随着信息化进程的不断推进, 口令所面临的“可记忆与抗猜测” 要求之间的矛盾愈发凸显.“可记忆”要求口令尽量短、有规律、不复杂, “抗猜测” 要求口令尽量长、无规律、越复杂越好.令人更为担忧的是,近年来频繁发生的大规模口令泄露事件(如32 亿条包含邮箱和口令的COMB 数据合集[13]), 为攻击者猜测用户口令提供源源不断的素材.同时攻击者的能力也在不断增强, 如深度学习技术的进展为提高口令猜测效率提供了潜在的新途径[14–16].鉴于口令往往作为保护信息系统的第一道防线, 从攻击者的视角出发, 深入研究口令在猜测攻击下的安全强度变得尤为重要.
口令猜测方法根据技术路线的不同, 主要可分为三类.第一类为基于规则的猜测攻击, 如将口令password 通过首字母大写、字母a 跳变为字符@ 的规则, 转化为P@ssword.此类方法最早可追溯到1979 年, Morris 和Thompson[17]首次设计了一系列启发式变换规则, 以生成字典中单词的变体, 用于口令猜测攻击.随后, 一些口令破解工具(如John the Ripper[18]和Hashcat[19]) 通过利用GPU 来进行大规模自动化的猜测攻击, 进一步推动了基于规则的口令猜测技术的发展.时至今日, 这些工具仍是现实攻击者进行离线口令猜测攻击的主要手段之一.
第二类为基于统计学方法的猜测攻击.这类方法主要通过统计训练口令字典中基本元素的频次来设计概率模型, 典型的代表有马尔科夫链(Markov[20]) 和概率上下文无关文法(PCFG[21]).早在2005 年,Narayanan 和Shmatikov[20]提出了一种基于马尔科夫链的口令猜测模型.该模型通过估算相邻两个字符之间的概率, 揭示了利用自然语言处理(NLP) 技术来生成口令猜测的潜力.在此基础上, Ma 等人[22]于2014 年在马尔科夫链上引入了多种归一化和平滑技术, 以克服原始模型存在的数据稀疏和过拟合问题.此外, 在2009 年, Weir 等人[21]提出了基于概率上下文无关文法的口令猜测模型PCFG.该模型将口令视为多个独立的、不同类型的字符串组成(如字母段L、数字段D 和特殊字符段S), 利用基于统计数据获得的文法规则生成口令结构模板, 随后用训练字典中的字符串填充这些模板.此后, 大量基于PCFG 的猜测方法被陆续提出.例如, 在2014 年, Veras 等人[23]进一步对字母L 段进行语义挖掘, 提出了融合语义信息的Semantic-PCFG 算法.
第三类为基于机器学习/深度学习技术的猜测攻击.这类方法通常将口令猜测视为文本生成任务, 利用现有的机器学习模型学习口令的结构与语义特征.训练完成后, 模型可自动生成大规模猜测.2016 年,Melicher 等人[14]首次将深度学习技术引入到口令猜测领域, 并提出了基于循环神经网络的口令猜测模型FLA (fast, lean, and accurate).与Markov 模型类似, FLA 也通过n阶字符串预测下一个字符, 不同之处在于, FLA 在训练完成后, 自动为字符表中的每个字符都分配一个较小的(非零的) 概率, 作为输入n阶字符串的预测结果.该方法通常在较大猜测规模(如>1010猜测数) 开始展现优势.近年来, 随着生成式对抗网络(GAN) 技术在自然语言处理(NLP) 领域的发展, 涌现出一批基于GAN 的口令猜测模型, 如PassGAN[15]和条件性口令猜测(conditional password guessing, CPG)[16].此外, 还有研究将深度学习技术与传统的基于规则或基于统计学的口令猜测方法相结合, 进一步提升了现有猜测方法的攻击效率.例如, 2021 年, Pasquini 等人[24]提出了自适应动态规则调整攻击方法AdaMs (adaptive, dynamic mangling rules).该方法利用深度学习技术优化了口令与对应规则列表的匹配优先级, 显著提升了(基于规则的) 字典攻击的攻击效率.
在研究口令猜测算法时, 如何准确且公平地评估其优劣是一个关键问题.当前, 学术界主要采用“猜测成功率vs.猜测数” 这一指标来评价不同算法的优劣, 即给定猜测数下, 算法能成功命中口令的比例越高, 算法越好.由于该指标与攻击者所拥有的计算资源和运行算法所需要的系统环境配置无关[25], 只取决于用户口令强度和算法自身的猜测能力, 因此, 这一评价标准逐渐成为公平对比各个口令猜测算法的重要手段.然而, 在现实世界中, 计算资源与环境配置往往是确定的, 在此情况下, 不同类型算法的计算效率差异巨大.例如, 在普通服务器上(CPU: Xeon Silver 4210R 2.4 GHz; GPU: GeForce RTX 3090), 基于统计学方法的PCFG[21]每秒可生成8 万猜测, 而基于机器学习技术的RFGuess[26]生成同样数量的猜测需要约10 分钟.虽然更换更好的硬件设备能提升对应算法的计算效率, 但这涉及到巨大的攻击成本差异.因此, 计算效率和攻击成本理应成为猜测算法的评价指标之一.
此外, 科学合理的实验设置也是评估猜测算法的重要因素.尽管当前关于口令猜测的研究众多, 但在实验设置的细节方面存在较大差异, 其中一些关键设置至今仍未形成普遍共识.在此有以下几个关键方面需要特别关注: 首先是数据集比例的划分方式.不同研究采用了不同的训练集和测试集比例, 如80% 对20%[15,16]、50% 对50%[21,27,28]甚至75% 对25%[26].与之紧密相关的是训练集和测试集的大小问题.以Veras 等人[29]的研究为例, 他们发现PCFG 算法在超过百万量级的训练集上, 进一步增加训练数据的规模并未显著提高猜测成功率.另一方面, Dell’Amico 等人[30]在对不同算法采用蒙特卡洛方法进行评估时, 仅仅选用了1 万大小的测试集, 而Pal 等人[31]的实验结果表明, 当测试集达到10 万时, 基于口令重用的定向猜测算法的破解成功率趋于稳定(误差小于0.1%).其次, 训练集和测试集的选取问题也具有重要意义.在现实场景中, 攻击者往往是聪明的, 因此, 所使用的训练集和测试集的口令分布应越接近越好,即训练集与测试集在语言、服务类型和口令策略上应尽可能保持一致.然而, 当前的研究, 包括一些最新的工作(如文献[16,32,33]), 在实验设置时并未明确考虑这些关键细节.
进一步, 还需要考虑训练集和测试集之间的交叉问题.一些研究(如文献[15,21,33]) 在测试集中去除了训练集中已出现过的口令, 以评估算法生成新口令的能力, 即泛化能力.然而, 与之相对应的是, Wang等人[26]的研究指出, 攻击者在现实场景中往往无法了解被攻击目标的口令分布, 因此更建议保留交叉部分, 避免去除测试集中与训练集重合的部分.此外, 生成训练集中已存在口令的能力, 即重新排列训练集中的部分口令, 也能够反映猜测算法的拟合能力.
面对以上关键问题, 需要深入探讨: 不同比例的训练集与测试集划分是否对猜测算法评估结果产生显著影响?使用何种规模的训练集与测试集是科学合理的?是否有必要保持训练集与测试集的分布尽可能一致?是否应该去除训练集与测试集的重合/交叉部分?回答这些问题将有助于确立更科学的实验设置原则, 以便更准确地评估口令猜测算法的性能(包括攻破率和计算效率).
目前, 针对口令猜测的研究主要聚焦于算法本身, 缺乏对算法在不同场景下实际应用效果的系统讨论.一些基于机器学习的猜测算法(如FLA[14]), 受限于口令生成速度, 更适合作为PSM (password strength meter) 来实际应用.虽然基于统计学的猜测算法(如PCFG[21]) 生成速度较快, 但其往往受限于训练集,在大猜测数下的表现出现瓶颈.此外, 在现实情况下, 攻击者可能采取多种手段来进行口令猜测, 如何在给定计算资源的条件下, 选取更高效的猜测算法是一个值得深入探讨的问题.
另一个值得关注的方向是口令文件泄露检测, 即利用猜测算法生成诱饵口令(decoy passwords, 即honeywords[27,34]), 并与用户真实口令混合存储, 通过监测诱饵口令的登录尝试来判断口令文件是否泄露.然而, 学术界提出的各类口令强度评价算法(特指基于猜测算法的PSM) 和诱饵口令机制, 均未在实际系统中得到广泛部署, 阻碍它们实际应用的障碍与挑战也是一个值得重点关注的议题.
无论是面向国家安全还是个人用户的数字资产保护, 对口令猜测技术进行全面深入研究都具有迫切现实需求.近年来, 口令猜测研究逐渐成为一个热点, 涌现出了一大批关于口令猜测的研究成果(如文献[16,24,26,32,33,35]).2023 年, Yu 等人[36]回顾了2016–2023 年学术界提出的37 种口令猜测算法,并展示了口令猜测领域相关研究的交叉引用趋势.然而, 该研究主要关注基于神经网络的口令猜测算法,并未对不同口令猜测算法之间的性能差异进行深入探讨, 缺乏对已有算法优劣的系统总结.为此, 本文对口令猜测领域的已有主流算法进行了全面的梳理和分类, 并指出该领域存在的研究局限性和未来值得研究的方向.这将有助于后续的研究者审视最新方法, 并避免重复研究.
综上, 本文将首先基于大规模真实口令数据, 分析用户口令构造规律, 挖掘用户的脆弱口令行为, 再围绕不同类型的口令猜测算法, 从技术原理、实验设置(包括算法评估指标)、实际应用与未来研究方向4 个方面, 对国内外最新口令猜测研究进展进行综述.
2 用户口令规律分析
自2009 年以来, 大规模口令数据泄露事件频繁发生.例如, 2009 年, 社交媒体应用开发商Rockyou遭遇黑客攻击, 导致其3200 万用户的口令以明文形式被泄露[37]; 2011 年, 国内多家知名互联网公司(如CSDN、天涯、人人网) 发生大规模用户口令数据泄露[38]; 2012 年, 知名云存储服务商Dropbox 遭遇数据泄露, 6800 万个账户信息被黑客窃取[39]; 2014 年, 国内知名购票软件12306 发生数据泄露, 泄露信息包含用户账号、明文口令、身份证和邮箱等多种个人信息[40]; 2015 年, 知名的游戏直播平台Twitch 遭遇数据泄露事件, 导致约5500 万用户口令文件被泄露[41]; 2016 年, Yahoo 公司宣称其数十亿用户信息在2013 年被泄露, 包括姓名、邮箱和口令等[42]; 2017 年, DNA 检测公司MyHeritage 遭遇黑客入侵, 约9300 万用户的电子邮箱和口令被泄露[43]; 2018 年, 华住集团发生数据泄露, 包括1.3 亿条身份信息、2.4亿条开房记录等, 共计约5 亿条信息[44]; 2019 年, 1.62 亿Dubsmash (多媒体应用) 用户数据被泄露, 包括姓名、用户名和口令等[45]; 2020 年, 知名视频会议软件zoom 的53 万用户口令被泄露[46]; 2021 年,Nitro PDF 数据库超7700 万条数据被泄露, 包括邮箱、用户名和口令等[47]; 2022 年, 黑客入侵了著名的宠物游戏网站Neopets 的数据库, 并窃取了6900 万用户的个人数据, 包括用户名、邮箱和口令等[48].这些源源不断泄露的口令数据为口令猜测研究提供了有力的数据支撑.
本文首先将从流行特性、语言依赖性、长度分布、口令重用、结构和语义特征(如包含个人信息) 等6 个方面挖掘用户的脆弱口令行为, 分析用户口令构造规律.
2.1 数据集简介
表1 展示了本文所采用的口令数据集, 总共包括6 个中文和7 个英文数据集, 涵盖了多种类型, 如邮箱、社交网站、游戏论坛等.其中, 12306、Rootkit 和ClixSense 包含姓名、邮箱、用户名、生日等在内的4∼6 种个人信息.鉴于包含个人可识别信息(PII) 的数据集通常规模较小, 主要用于与PII 相关的分析和实验.在进行口令结构和语义特征分析时, 本文将主要使用不包含PII 的10 个数据集.这些数据集在学术界被广泛应用(见表1 最右一列).
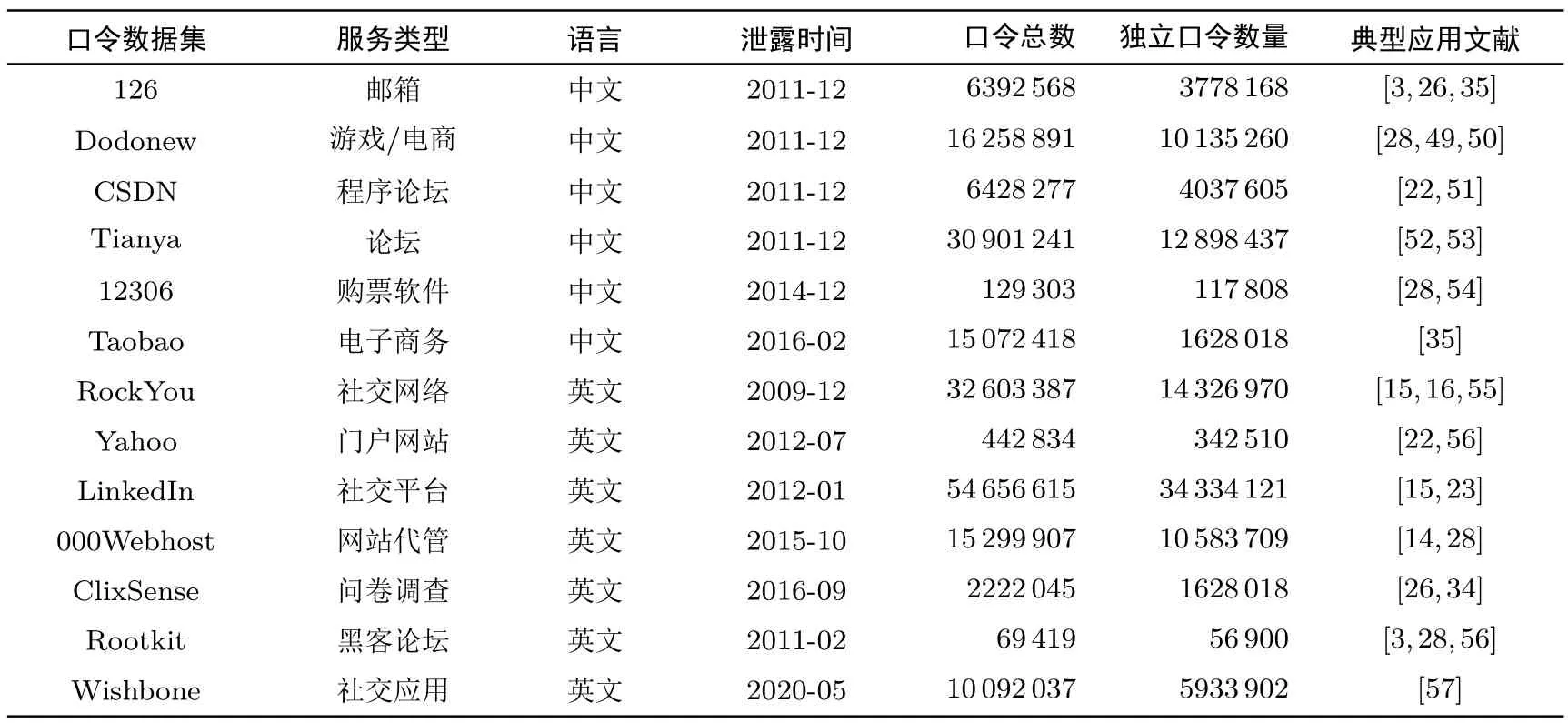
表1 本文所使用口令数据集的基本信息Table 1 Basic information of password datasets used in this paper
2.2 流行口令
流行口令(popular password) 是指用户广泛使用的、相对简单且常见的口令.这些口令通常由短数字、常见单词、常见短语或字符组合构成, 因其普遍性而容易被攻击者利用.表2 为不同数据集按频数排序后排名前十的流行口令及其对应的比例.由于空间限制, 在此仅展示具有代表性的9 个数据集, 其余数据集具有类似的规律.可以看出, 除了CSDN 与000Webhost 以外, 123456 在任何数据集中的流行度都占据第一的位置, 不受语言、文化和网站服务类型的影响.因为口令策略的原因, CSDN 与000Webhost的流行口令呈现出与其他数据集略微不同的特点.例如, CSDN 要求用户生成的口令长度必须大于等于8;000Webhost 的口令生成策略为长度至少为6, 且至少包含一个数字和字母.为了应对这些策略, 用户会采取一些“聪明” 的修改, 如123456→123456789, 123456→a123456.这样的修改显然是徒劳的, 攻击者只需对猜测字典进行简单的调整, 即可快速破解出这些“新的” 流行口令.此外, 还可以观察到一些流行口令与特定网站或平台密切相关的特点.例如, 在Tianya 数据集中, 111222tianya 排名第10; 在Wishbone中, wishbone 排名第4; 在CSDN 数据集中, dearbook 排名第4 (dearbook 为CSDN 旗下书店的域名).而这些特征都是攻击者所努力挖掘的对象.
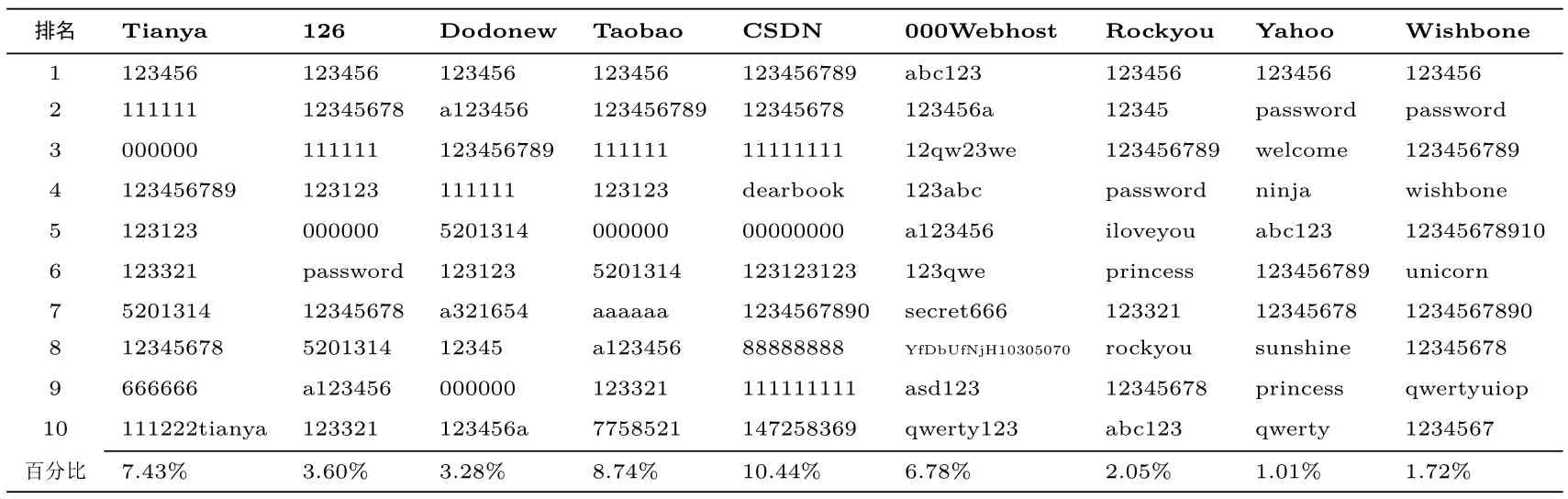
表2 各个数据集中最流行的10 个口令Table 2 Top-10 most popular passwords of each dataset
2.3 口令长度分布
表3 为不同口令数据集的长度分布.总体看来, 口令长度分布在不同数据集之间存在差异, 但绝大多数用户(>75%) 的口令长度都集中在6∼11 之间.除000Webhost 以外, 所有数据集长度大于15 的口令数量都很少(<1.1%).此外, 从长度分布中也能反映不同网站的口令策略.例如, Wishbone 数据集中,没有长度小于6 的口令, 这表明, 该网站的口令策略要求用户创建的口令长度必须大于等于6.类似地,CSDN 数据集中仅有2.2% 的口令长度小于8, 这表明CSDN 可能在开放注册不久后, 便要求其用户创建口令的长度至少为8.除了口令策略, 用户的安全意识也对口令数据集的长度分布有一定的影响.例如,000Webhost 的用户多为网站管理员, 其长口令的比例显著高于其他数据集, 即使与具有相似口令策略要求的网站(CSDN 和Wishbone) 相比, 000Webhost 长口令的比例也明显更高.

表3 口令长度分布Table 3 Password length distribution
2.4 口令字符组成和结构
表4 展示了不同数据集的口令字符组成分布.观察发现,中文用户创建口令时,大约29%∼64%的口令是纯数字,而10%∼23%的口令由纯小写字母构成;英文用户的口令呈现与其相反的趋势,大约25%∼42%的口令是纯小写字母, 仅有9%∼20% 的口令由纯数字构成.这意味着数字在中文用户口令中的地位与小写字母在英文用户口令中的地位相当.这种特性也导致了中英文用户的口令呈现出双相安全性[52]: 面对在线猜测时(即允许的猜测次数较小, 如1∼10 000), 英文用户口令抵御猜测攻击的能力优于中文用户; 面对离线猜测时(即允许的猜测次数较大, 如>105), 中文用户口令抵御猜测攻击的能力优于英文用户.
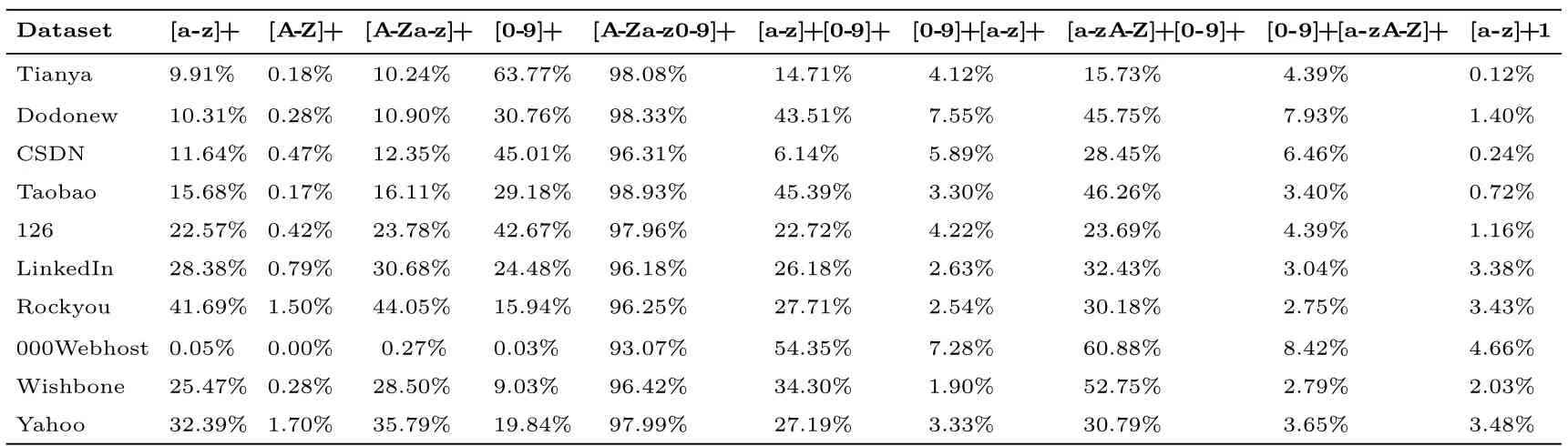
表4 每个数据集的口令字符组成结构Table 4 Character composition information about each password dataset
此外, 还有一些有趣的现象值得注意: 无论是中文用户还是英文用户, 都很少(占比约0.17%∼1.70%)采用纯大写字母作为口令; 有不可忽略的用户(占比约0.12%∼4.66%) 倾向于在口令末尾添加一个数字1; 绝大多数用户(占比>93%) 的口令都仅由字母和数字组成.这些特征的分析和挖掘, 将大大缩小攻击者的搜索空间, 进而提高他们的猜测效率.
2.5 基于个人信息构造口令
为了便于记忆, 用户通常在创建口令时会使用自己的个人信息.然而, 这种行为也带来了潜在的安全风险, 因为攻击者可以利用用户的这一脆弱行为, 大幅提高口令猜测的成功率.例如, Wang 等人[28]的研究结果表明, 当攻击者已知用户的姓名、生日、用户名、邮箱和手机号时, 仅需进行100 次猜测, 系统即面临实质性安全风险(猜测成功率约为20%).
表5 为四个不同网站的用户在创建口令时使用个人信息的情况(其中, PII-Dodonew 数据集是通过邮箱与12306 数据集匹配获得, 因为Dodonew 数据集本身不包含个人信息).观察发现, 两个中文网站的用户更频繁地使用个人信息来构建口令, 而两个英文网站的用户则相对更谨慎.这一现象极可能与网站的服务类型相关[52].例如, ClixSense 是一家付费问卷调研网站, 与金融相关, 而Rootkit 是一个黑客论坛, 其用户普遍具有较高的安全意识(这在文献[28] 中也得到了确认), 因此这两个网站的用户倾向于更谨慎地使用个人信息构建口令.
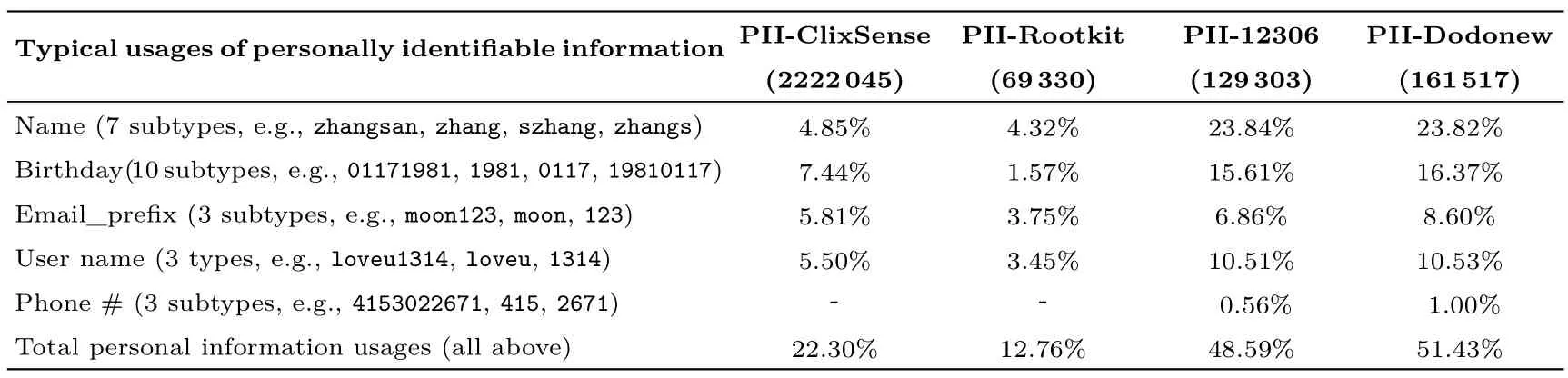
表5 用户口令个人信息使用比例Table 5 Percentages of users building passwords with their own personally identifiable information (PII)
总体看来, 虽然不同网站用户之间的口令创建行为存在差异, 但用户在口令创建过程中使用个人信息是一个较为普遍的现象(12.8%∼51.4%).这也提醒了网站和服务提供商需要采取有效措施来引导用户避免在创建口令时使用个人信息, 以减少潜在的安全风险.
2.6 口令语义分析
为了探究口令所包含的语义信息, 本文以Wang 等人[52]的研究为基础, 考虑9 种语义模型并构造4个语义字典.它们分别是单字符重复(如111111)、多字符重复(如123123)、规律性序列(如654321)、回文数(如123321)、键盘模式(如zxcvbn)、四种日期格式(完整年月日YYYYMMDD、部分年月日YYMMDD、月日MMDD 和年YYYY)、英文单词字典、英文姓名字典、拼音单词字典和拼音姓名字典.表6 为不同数据集口令所包含的语义信息.

表6 口令中所包含的语义信息Table 6 Popularity of dictionaries with different semantics in password set
口令与语义字典的匹配方式采用与文献 [23] 相同的最大语义覆盖原则.例如, 对于口令baobaolxy963, 可以将其拆分为以下几个部分: baoba([PinyinWordLower])、963([Keyboard]), 和baobao([PinyinWordLower, SegmentRepeat, PinyinNameAny]).研究目标是遍历这些可能的语义段(将语义片段数目记为n), 确保在语义段数目相同的情况下, 覆盖率最大.具体而言, 当n=1 时, 单个语义段baoba 的覆盖率为5/12、963 的覆盖率为3/12、baobao 的覆盖率为6/12, 最大覆盖率为6/12; 当n=2时, 两个语义段baoba+963 的覆盖率为8/12、baobao+963 的覆盖率为9/12、baoba+baobao 的覆盖率为6/12, 最大覆盖率为9/12; 以此类推, 循环退出条件为n>3 或者已经达到100% 覆盖率.
观察发现, 不论是中文用户还是英文用户, 其口令中都包含了丰富的语义信息.这些信息可以分为多种模式, 包括字符重复、规律序列、日期、键盘模式和语义字典(中文用户的口令对应拼音字典, 英文用户的口令对应英文单词字典).其中, 中文用户更倾向于在口令中使用日期信息, 尤其是年月日模式(如990525), 这可能与个人生日或重要纪念日有关, 也使得这部分用户的口令更容易遭受定向攻击.值得注意的是, 中英文用户在创建口令时都倾向于使用规律的序列(如654321, abcdefg), 这种现象在有口令策略要求的网站中尤为突出.例如, 在中文数据集中, CSDN 口令的规律序列占比最高(16.89%); 在英文数据集中, 000Webhost、Wishbone 和LinkedIn 中规律序列的占比排名前三.
2.7 口令重用
随着各种数字化网络服务的迅速发展, 用户需要管理的账户数量不断增加.研究表明, 通常情况下, 互联网用户需要管理约100 个口令[58].然而, 由于人类的记忆能力有限且难以稳定地记住如此多的口令, 用户不可避免地倾向于重复使用口令或对现有口令进行简单的修改(即间接口令重用).频繁发生的大规模口令数据泄露事件, 为攻击者提供了丰富的数据资源.一旦攻击者成功获取了用户在一个网站的口令, 就很容易攻破其重用相同或相似口令的其它账户.
Wang 等人[3]在2016 年对口令重用相关的研究进行了总结: 约21%∼51%的用户会直接重用已有口令, 有26%∼33% 的用户会间接重用口令.在此, 间接重用的衡量标准为新旧口令的相似度在[0.8,1] 之间,其使用的相似度指标为基于文氏距离、曼哈顿距离的文本相似度算法.以大规模口令泄露合集COMB[13]为例(包含超过32 亿独立的邮箱和明文口令对), 本文对用户多个口令的泄露现状进行了统计.具体而言,使用邮箱前缀进行匹配(例如, zhangsan123@google.com 与zhangsan123@yahoo.com 的前缀一致, 则认为这两个邮箱对应同一用户), 共计得到约14 亿数据条目, 其中16% 的邮箱前缀对应2 个口令, 6% 的邮箱前缀对应3 个口令, 10% 的邮箱前缀对应至少4 个口令.
更进一步, 本文从(通过邮箱前缀匹配得到的) 口令数目大于等于3 的数据条目中(共计约2.2 亿),随机选取3 个口令(分别记为pwA, pwB和pwC), 探究用户多口令重用的现状.特别地, 以基于编辑距离的相似度算法为例(相似度计算方式为s=1−EditDistance(pwA,pwB)/max(|pwA|,|pwB|), 相似度阈值设为0.5), 本文统计了用户3 个口令之间的相似关系, 详细结果如表7 所示.
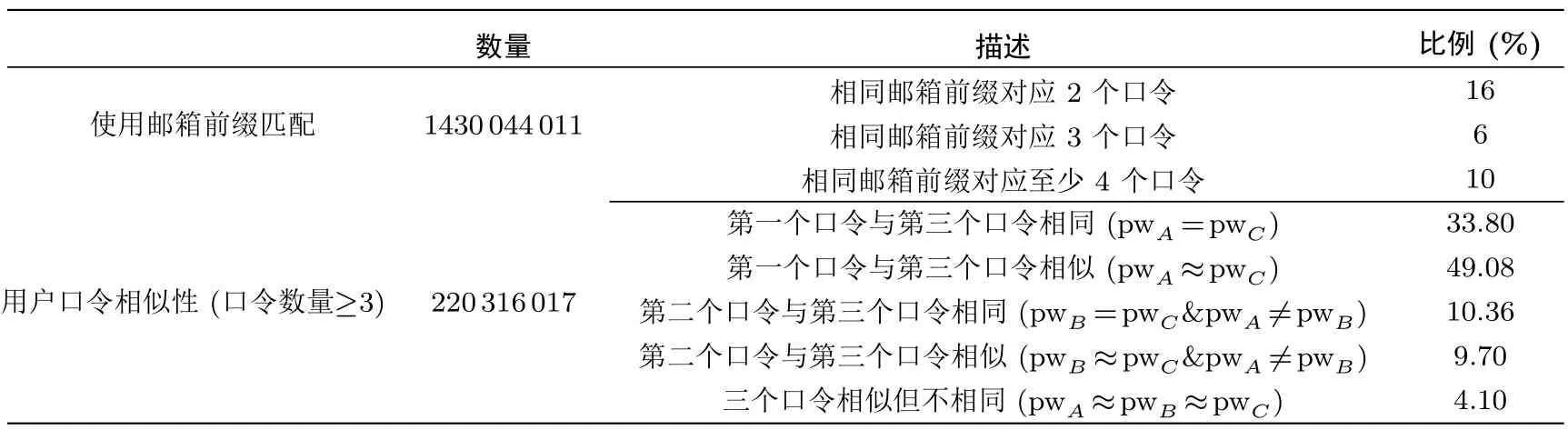
表7 用户口令重用统计Table 7 Statistics about password reuse
观察发现, 约有33.80% 的用户的第一个口令与第三个口令完全相同(pwA=pwC).此外, 约10.36%的用户的第二个口令与第一个口令不同(pwA ̸=pwB), 但与第三个口令完全相同(pwB=pwC).这表明,攻击者利用用户泄露的旧口令pwA直接攻击目标口令pwC的成功率为33.8%; 若攻击者再直接利用同一用户额外泄露的第二个旧口令pwB, 即可多增加10% 的猜测成功率.其次, 还发现大约4.1% 的用户的三个口令之间相似但不相同.这表明这些用户在创建多个口令时可能存在一定的规律模式.因此, 需要设计新的模型来更深入地理解用户多个旧口令之间的内在联系.
3 口令猜测攻击
口令猜测攻击根据技术路线的不同, 大致可分为三种类型.第一类为基于规则的猜测攻击, 此类方法通过设计各种口令变换规则, 然后应用于已有口令或单词, 更多依赖于攻击者的经验.第二类为基于统计学方法的猜测攻击,例如,基于概率上下文无关文法(PCFG[21])、基于马尔科夫链的方法(Markov[20,22]).这些方法使用数学和统计模型来分析和生成口令, 可以考虑上下文语法规则, 提高了口令猜测的成功率.第三类为基于机器学习的猜测攻击, 近年来这一领域得到了广泛的关注.学者们尝试采用各种复杂的神经网络结构(如RNN[14]、GAN[15]、WAE[16]) 来解决传统统计学方法存在的数据稀疏和过拟合问题.此外, 还有研究(如文献[24]) 将机器学习技术与开源工具(如Hashcat[19]) 相结合, 大大提升了原始工具的猜测效率.下面将对这三类方法中具有代表性的算法/工具/模型/框架进行介绍.图1 和表8 对2005 年以来的具有代表性的口令猜测算法进行了分类和总结.

图1 口令猜测算法的发展脉络和分类Figure 1 Evolutionary trends and classification of password guessing algorithms
表8 主要口令猜测算法总结Table 8 Summary of mainstream password guessing methods
3.1 基于规则的攻击方法
3.1.1 启发式算法
不同于传统的暴力破解方法, 启发式算法很大程度上依赖于攻击者的经验.其核心思想是观察用户在创建口令时的脆弱行为, 然后运用各种启发式技巧以提高口令猜测的效率和成功率.其中一种常见的技巧是基于规则的变换, 攻击者会利用口令中常见的规律和模式, 对已有口令或单词进行多种变换, 例如首字母大写、尾部字符(串) 的插入/删除、字符替换(如将字符a 替换为字符@)、字符串反转等.早期, 仅有一些欧美机构进行了零星的研究.例如, 1979 年, Morris 和Thompson[17]设计了各种启发式变换规则,用于生成字典中单词的变种, 以进行口令猜测; 1990 年, Klein[64]“精心设计” 了口令猜测的顺序, 用于攻击15 000 个经过DES 加密的真实口令; 1999 年, Thomas[65]基于用户群体的领域特征构建了口令猜测字典, 用于攻击2500 个经过DES 加密的真实口令.
尽管此类方法缺乏严格的理论基础和系统性, 但在特定场景下, 如果设计合理, 其猜测成功率也不容小觑.例如, 2014 年, Das 等人[56]提出了一种基于用户旧口令和规则变化的启发式口令猜测算法.该算法按照预定义的规则顺序对用户已有的原始口令应用八类变换操作(如插入、删除、大写等).在每个变换阶段之后, 检查生成的口令是否已经猜测到了目标口令.在小猜测数下(如100 次), 该算法的猜测成功率达到30%, 远优于漫步猜测算法, 但它也存在一些固有的缺陷: 它假设所有用户都以固定的优先级选择口令变换规则, 这不符合用户重用口令的真实行为; 生成口令猜测时, 该算法仅考虑了一种规则变换情况, 没有考虑两种或更多规则变换的组合情况, 这无法捕捉用户重用口令时的复杂修改行为.
3.1.2 口令破解工具
Hashcat[19]和John the Ripper(JtR)[18]是两款最为流行的口令破解工具, 它们在学术研究和实际应用中都发挥着重要作用.这两个工具包的运行效率经过高度优化, 能充分发挥多核处理器和GPU 提供的并行计算性能.它们提供多种攻击模式, 如掩码攻击、规则变换和字典组合等, 将传统的纯暴力破解攻击转化为更为智能和有针对性的搜索策略.虽然Hashcat 和JtR 各自有一些独特的指令/模式, 但这两个工具共享几乎相同的规则变换方法.值得注意的是, 它们在应用规则变换时的策略略有不同.具体而言,Hashcat 遵循以单词为主的顺序(word-major order), 即在考虑下一个字典中的单词之前, 会将规则集中的所有规则应用于当前单词.相反, JtR 遵循以规则为主的顺序(rule-major order), 即在应用下一个规则之前, 将当前规则应用于字典中的所有单词.这种差异对于研究基于规则的口令破解方法具有重要意义.
尽管学术界提出了一系列口令猜测算法, 并声称其猜测成功率优于口令破解工具Hashcat/JtR, 但这些比较实验往往采用了破解工具的默认配置, 无法反映经验丰富的攻击者的真实能力.2015 年, Ur等人[67]调研了研究人员常用的口令猜测算法与专业攻击者实际采用策略之间存在的差异, 强调了仅仅依赖单一破解算法作为口令安全性度量存在偏差, 并首次提出了结合各类猜测算法/工具的理想指标Min_auto.该指标可理解为采用同一口令在不同猜测方法下猜测数的最小值作为其安全性的度量.
事实上, 经验丰富的攻击者通常会精选合适的字典和规则, 并根据中间结果和破解成功率灵活地调整攻击策略.例如, 在文献[68] 中, 详细描述了三名攻击者如何利用专业经验快速破解约90% 的口令.在此,以第一位攻击者(记为攻击者A) 的破解策略为例, 进行简要介绍.
攻击者A的破解策略可以分为三个主要阶段, 每个阶段采用不同的攻击方法.以下是对这三个阶段的简要概述: 在第一阶段, 他采用了包括暴力破解和基于字典的攻击在内的多种攻击策略.具体而言, 他首先尝试了1 到6 位长度的所有字符组合, 包括大小写字母、数字和特殊字符.然后, 他分别对7 或8 位长度的纯小写字母和纯大写字母进行破解尝试.接着, 他尝试了1 到12 位长度的纯数字组合.此外, 他还应用了一个多年来精心筛选的字典, 并结合了best64 规则集进行攻击.在已破解的口令的基础上, 他还使用了d3ad0ne 规则集进行进一步尝试.在此阶段, 攻击者A成功破解了62% 的口令, 仅耗时16 分钟.在第二阶段, 攻击者A采用了混合攻击策略, 结合了字典和掩码.他依次尝试在字典中每个口令的末尾添加了2 个字符(数字或特殊符号)、3 个字符(数字或特殊符号)、4 个数字, 以及3 个小写字母和数字的组合.在此阶段, 攻击者A再次成功破解了16% 的口令, 过程耗时5 小时12 分钟.最后, 在第三阶段, 攻击者A采用了hashcat 掩码模式内置的马尔科夫优化, 将先前成功破解的口令用作训练集, 并结合自定义字典和规则, 进一步成功破解了10% 的口令, 耗时14 小时59 分钟.需要注意的是, 这一破解流程具有明显的阶段性, 每个阶段的难度逐渐增加, 其根本原因在于口令的分布服从Zipf 分布[49,57]: 流行的口令和罕见的口令, 都占据用户群体中相当大的比例.
近年来, 陆续有研究者对如何更合理/高效地利用口令破解工具展开了研究.例如, 在2019 年, Liu 等人[69]介绍了一种分析和高效处理破解工具(如Hashcat 和JtR)的技术.作者提出了两种新的操作,即规则反转(rule inversion) 和猜测计数(guess counting), 通过这些操作, 他们能够快速分析口令在此类工具下的安全强度而无需列举所有可能的猜测; 在2021 年, Zhang 等人[70]设计了一个实用的口令数字语义提取工具, 基于经验性分析, 他们提出了两种新的操作(operations, 即构建规则集的基本单位), 并生成了1974 个数字语义规则.通过对JtR 和Hashcat 规则引擎和运行逻辑的优化, 作者实现了JtR 和Hashcat对所提出新操作的支持; 在2021 年, Pasquini 等人[24]利用深度学习技术对口令与规则的适配度进行了优化, 提出了基于规则的自适应攻击算法ADaMs (详细描述见第3.3.5 节); 2022 年, Di Campi 等人[71]对规则依据频数进行排序, 发现使用大规模字典结合少量高效的规则更为有效; 同年, Li 等人[63]采用无监督聚类方法生成更为有效的口令规则集, 使得字典攻击的猜测成功率在大猜测数下高于现有的口令猜测算法.具体而言, 作者首先使用Damerau-Levenshtein 距离和Jaro-Winkler 距离作为度量指标, 运用改进的无监督聚类算法DBSCAN 对口令进行聚类.在每个聚类中, 他们选择了与所有其他元素的距离之和最小的字符串作为基准字符串(base string).接着, 利用Damerau-Levenshtein 距离算法, 从基准字符串到目标字符串生成了一系列插入、删除和替换操作, 形成单个类别的规则集.最后, 他们将从所有聚类中生成的规则集合并, 并按照规则出现的频数进行排序, 再通过Hashcat[19]工具, 将基础字典与规则集结合生成最终的猜测集.
3.2 基于统计学的攻击算法
3.2.1 PCFG
2009 年, Weir 等人[21]提出了一个基于概率上下文无关文法的漫步口令猜测算法PCFG.该算法将口令字符分为三种类型: 字母段L、数字段D 和特殊字符段S, 并假设不同类型的字段之间相互独立.它将口令按照不同字符类型和对应子串长度转化为中间结构(模板).例如, 口令password123! 可以表示为L4D3S1, 其中L4代表长度为4 的字母段wang, D3代表长度为3 的数字段123, S1代表长度为1 的特殊字符段!.其训练和生成过程简要描述如下(如图2 所示): 首先, 从训练集中统计出各类口令结构(如L4D3S1) 及其实例化(如L4→wang) 所对应的概率; 然后, 通过从训练数据集中学习到的相同长度的实例化(instantiations) 替换这些“L、D、S” 标签, 生成候选口令及其对应的概率; 最后, 对生成的口令依照概率大小排序形成猜测集.例如, 口令wang123! 在PCFG 模型下的概率可以计算为Pr(wang123!)=Pr(L4D3S1)×Pr(L4→wang)×Pr(D3→123)×Pr(S1→!).

图2 PCFG 训练与生成过程示意图Figure 2 Training and generation process of PCFG
PCFG 受到后续研究者的持续关注, 学者们不断扩展和优化其在口令猜测领域的应用, 衍生出一系列基于PCFG 的改进/新型猜测算法.例如, 2014 年, Veras 等人[23]对口令中包含的语义信息进了深入挖掘, 提出了融合语义的PCFG 算法.该方法主要分为三步:
首先, 借助语料库对口令进行分词处理.例如, 口令loveblue0507 分词后的结果是love、blue 和0507.在其中, 字母构成的部分被称为“word 段”, 而数字和特殊字符构成的部分被合称为“gap 段”.
其次, 对这些“word 段” 进行词性标注, 即为每个字段赋予一个相应的词性类别.举例来说, blue 被标注为名词单数(NN).接下来, 进行词性分类与泛化操作.对于“word 段”, 如果该段所属词汇在源语料库中, 那么它会被划分至相应的语料库类别(如“月份”、“女性名字” 等).否则会利用Wordnet (一种同义词集合工具) 将其类别归纳为一个通用的专业表达形式.例如, 将love 分类为love.n.01, 表示喜爱的第一个名词含义; 词性分类完成后, 需要构建一个树模型进行抽象泛化, 例如, soldier 的语义标签为worker.n.01 ( “worker” 的第一个名词义项), 其泛化后的结果为soldier.n.01.
最后进行猜测生成, 该过程和原始PCFG[21]类似.例如, 生成口令youlovethem2 的概率计算公式为: Pr(youlovethem2) = Pr(N1→[PP][love.v.01.VV0][PP][number])× Pr([PP]→you)×Pr([love.v.01.VV0]→love)×Pr([PP]→them)×Pr([number]→2).
2014 年, Ma 等人[22]发现, 利用原始训练集的实例化(instantiations)来填充PCFG 的字母段L,其效果通常要优于从外部引入字典; 2015 年, Houshmand 等人[59]通过向上下文文法中引入键盘模式(如qwerty) 和多词模式(如boatboat) 改进了原始PCFG 的破解成功率; 2019 年, Wang 等人[52]对规律性的长结构(如D1L1D1L1D1L1) 进行了优化, 并引入拼音和姓名字典至原始PCFG 的字母段L, 改善了PCFG 在中文数据集上的破解成功率; 同年, Zhang 等人[50]利用改进的Markov 模型来生成PCFG 中L、D、S 段中的填充内容, 提升了原始PCFG 的泛化能力; 2020 年, Hranický 等人[61]提出了一种使用概率文法进行分布式破解口令的技术.其核心思想是将部分生成的句法形式分布到多个节点上, 从而减少了需要在网络中传输的数据量, 提高了破解口令的效率; 2021 年, Han 等人[62]提出了一种面向长口令的TransPCFG 框架.其核心原理在于从基于短口令训练的PCFG 模型(简称PCFGshort) 中提取有效的语法信息, 并将这些信息传递到基于长口令训练的PCFG 模型(简称PCFGlong) 中.同时, 还根据PCFGshort 中的结构信息来动态调整PCFGlong 中的结构信息, 从而提高了PCFG 针对长口令的破解成功率; 此外, 还有研究人员将个人信息标签(如姓名、生日、用户名、邮箱、手机号等) 引入PCFG, 提出了基于PCFG 的定向口令猜测算法, 如文献[28,54].
3.2.2 Markov
在2005 年, Narayanan 和Shmatikov[20]首次将马尔可夫模型(Markov) 引入到口令猜测.Markov模型(又称n-gram 模型) 有阶的概念,d阶Markov(d=n+1) 的核心假设是, 当前口令字符仅与和它对应的前d个字符有关, 与其它字符无关.例如, 3 阶Markov 模型对口令abc123 的概率计算如下:Pr(abc123)=Pr(a)×Pr(b|a)×Pr(c|ab)×Pr(1|abc)×Pr(2|bc1)×Pr(3|c12), 其中Pr(3|c12) 的计算方式为字符串c12 后是3 的频数除以c12 后有字符的频数, 其余条件概率的计算方式与之相同.
当Markov 模型的阶数过大时, 会出现数据稀疏的问题.例如, 当阶数为5 时, 若训练集中没有出现abcde1 这样的字符串, 那么转移概率Pr(1|abcde) 的计算结果为0.此外, 原始Markov 模型所生成的所有口令的概率加和不等于1.0.例如, 若训练集为{ab,abc}, 那么1 阶Markov 模型计算口令ab 的概率为Pr(ab)=Pr(a)×Pr(b|a)=1, 如果该模型再生成其他口令, 概率总和显然将大于1.0.
为了解决这些问题, 2014 年, Ma 等人[22]提出了一系列平滑(如Laplace 平滑) 和正规化方法(如End-symbol 方法), 实验结果表明使用End-symbol 方法的Backoff 模型表现最优, 在此对其进行简要介绍.End-symbol 是指在每个口令的末尾增加一个终止符号(记为⊥), 在训练时, 将其视为普通字符纳入统计; 在生成时,⊥可以出现在除了开头以外的任何位置,标志着单个口令生成完毕.仍以{ab,abc}为例,在对每个口令增加终止符后,1 阶Markov 模型计算口令ab 的概率变为Pr(ab)=Pr(a)×Pr(b|a)×Pr(⊥图3 为使用正规化方法的Markov 模型的训练和生成过程示意图.Backoff 是一种变阶Markov模型, 当某个字符所对应的d阶前缀的频数小于某个阈值时, 模型启用回退(backoff) 机制, 使用该字符对应的更短的前缀(如d −1 阶前缀), 直至该字符所对应前缀的频数满足阈值.例如, 当阶为4, 计算转移概率Pr(1|wang) 时, 如果字符串wang1 的频数不满足阈值, 而ang1 的频数满足阈值, 则计算转移概率Pr(1|ang)×ω(wang) 来代替原始的Pr(1|wang), 其中ω(wang) 是一个与所有以wang 开头的长度为5的字符串有关的值, 作用是将概率归一化, 使得整个口令空间的概率总和仍为1.0.

图3 Markov 训练与生成过程示意图Figure 3 Training and password generation process of Markov model
2015 年, Dürmuth 等人[66]对原始的Markov 模型的口令生成过程进行了优化, 提出了OMEN 模型, 其核心原理在于将Markov 模型中字符的概率值映射为等级, 使得模型可以(在整体层面) 按照概率降序生成候选口令, 从而大大提升了生成口令猜测的速度.
3.2.3 基于PCFG 的定向口令猜测框架TarGuess
2016 年, 基于PCFG[21]、Markov[22]和贝叶斯理论等统计计算理论, Wang 等人[28]提出了一个定向口令猜测理论框架TarGuess, 涵盖4 种基于不同个人信息组合的定向猜测攻击算法和3 个理论攻击模型.具体而言, 他们根据个人信息在构造口令时的作用和隐私程度, 将个人信息分为三类.第一类为能够直接用于构造口令的显式PII (称为Type-1 PII), 如姓名和生日; 第二类为隐式PII (称为Type-2 PII),如性别和受教育程度等, 它们虽然不能直接作为口令的一部分, 但它们会影响用户的口令创建行为; 第三类为用户的认证凭证信息, 如口令.根据攻击者所获取的个人信息的不同, TarGuess 框架主要刻画了四种最具代表性的定向猜测场景: (1) 已知用户的Type-1 PII; (2) 已知用户已泄露的旧口令; (3) 同时已知用户的个人信息和已泄露的旧口令; (4) 在场景#3 的基础上, 额外使用了目标用户的Type-2 PII (如性别).TarGuess 猜测框架图如图4 所示.
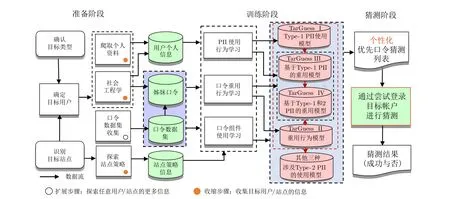
图4 TarGuess 猜测框架图[28]Figure 4 An architectural overview of TarGuess [28]
以TarGuess-I[28]为例, Wang 等人在PCFG[21]原有的字母L、数字D 和特殊符号S 标签的基础上, 引入了基于类型的个人信息标签(如姓名、生日、邮箱、用户名等).例如, 使用N 代表姓名信息, N1表示姓名全称, N2 表示姓名全称的缩写, N3 表示姓氏,···; 使用E 表示邮箱信息, E1 表示邮箱前缀的全称, E2 表示邮箱前缀的第一个字母段,···.不难发现, 新标签与原有的L、D、S 标签的不同之处在于,其下标数字不再代表长度, 而是代表不同的类型.通过这种表示方式, 可以有效避免使用长度划分个人信息[54]所带来的对字段的子类型不敏感的问题.
TarGuess-II 综合考虑了结构级(如L3D3→L3D3S2) 和字段级(L3:abc→L4:abcd) 两种口令修改变换方式, 并借鉴图同构的概念, 将新旧口令的结构级修改行为映射为传统PCFG 的结构变换.在此基础上, 利用Markov 模型来模拟字段内部的修改过程, 最终构建出一个完整的口令变换上下文无关文法模型.TarGuess-III 在TarGuess-II 的基础上, 引入了基于类型的PII 标签(与TarGuess-I 一致), 构建了一个可识别PII 的口令重用文法.TarGuess-IV 则通过引入贝叶斯理论, 将性别这一无法直接用于构造口令的隐式个人信息融入猜测模型, 其本质是对生成的猜测进行概率调整.
2020 年, Xie 等人[72]在TarGuess-I[28]原有个人信息标签类型的基础上, 增加了键盘模式、流行口令标签和特殊字符串标签, 提出了TarGuess-I+, 进一步提升了原始TarGuess-I 的猜测成功率.
3.3 基于机器学习技术的攻击算法
3.3.1 基于循环神经网络的口令猜测模型
2016 年, Melicher 等人[14]首次将深度学习技术用于口令猜测, 提出了基于循环神经网络(RNN) 的口令猜测模型FLA.该模型由3 层长短期记忆网络(LSTM) 和两层全连接层构成.其核心思想是通过口令中先前的字符序列来预测下一个字符出现的概率, 本质上是一个字符级的语言模型.与Markov 模型[22]的不同之处在于, FLA 模型在输入字符前缀后, 能自动为字符表中的每个字符都分配一个非零的概率, 而不是通过启发式的平滑技术(如Laplace 平滑).这使得FLA 相比Markov 模型具有更好的泛化性.
2019 年, Xia 等人[55]将LSTM 与PCFG 结合, 提出了口令猜测模型PL(PCFG+LSTM).该模型首先将训练集中的口令转换成结构段的形式(如password123!→L8D3S1), 再将结构段序列用于LSTM网络的训练; 模型训练完成后, 可生成一系列结构段序列, 再使用与原始PCFG 一致的方式对这些结构段进行相应填充.为了在不同测试集中能达到普遍较优的猜测效果, 作者进一步训练了多个PL 模型, 将这些模型的输出(即结构段及其对应概率) 相结合, 并进行权重选择, 再通过原始口令数据集训练的CNN 分类器判断新生成口令的来源, 最后通过设计的阈值判断生成口令是否是通用的(general), 作为接受和拒绝生成口令的依据.此过程构成了多源口令猜测方法GENPass.2021 年, Wang 等人[73]在PL 模型的基础上, 利用循环神经网络(RNN) 来生成PCFG 的结构段以及L 段的填充内容, 提出了PR+ 模型, 降低了模型对大训练样本的依赖.
3.3.2 基于生成式模型的口令猜测算法
2019 年, Hitaj 等人[15]首次将生成对抗网络(GAN[74]) 引入到口令猜测领域, 提出了PassGAN 模型, 它由生成器G 和判别器D 构成.不同于FLA 模型[14]的自回归生成方式, PassGAN 学习整个口令的字符分布.在训练过程中, 生成器G 接收随机噪声向量作为输入, 旨在生成与真实口令样本相似的假口令样本.判别器D 对来自训练数据集的真实口令样本和生成器生成的假口令样本进行区分, 从而提供反馈.生成器G 根据判别器D 的反馈逐步调整模型参数, 生成更逼真的假口令样本, 使其分布逐渐接近训练集中真实口令样本的分布.在训练完成后, 只需不断向生成器G 提供噪声向量, 就能生成口令, 直到达到所需的猜测集大小.图5 为GAN 用于口令猜测的示意图.不同于传统方法(如PCFG[21]和Markov[22])通过概率统计建立精确的口令概率分布模型, 基于GAN 的口令猜测模型无法为生成的口令样本赋予概率并排序.实验表明[15], 要达到与PCFG 和Markov 相同的猜测成功率, PassGAN 至少需要生成高一个数量级的猜测.尽管该方法的猜测成功率不如PCFG 和Markov 模型, 它显示了GAN 在生成口令方面的巨大潜力, 也为后续研究提供了新的思路和方向.
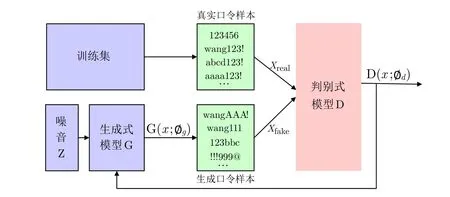
图5 基于GAN 的口令猜测模型Figure 5 GAN-based password guessing model
2021 年, Pasquini 等人[16]指出, 口令的离散表征使得生成器在训练过程中难以正确地反映数据分布, 从而导致训练过程的不稳定性; 此外, 生成器不能很好地学习训练数据的离散特性, 使得判别器可以轻易区分真实数据和生成数据, 限制了生成器的改进空间.为此, Pasquini 等人[16]对PassGAN 进行了改进.具体而言, 他们在每个口令字符的one-hot 编码表示上添加了小幅的噪声(通过一个超参数控制噪声的大小), 并在添加噪声后重新归一化了每个字符的分布, 以此来缓解离散特征带来的不稳定性.在模型架构层面, 作者在生成器中采用了批归一化(batch normalization), 从而可以更有效地使用更深的残差瓶颈块(residual bottleneck blocks).实验表明, 改进后的GAN 模型在大猜测数下(>108) 的猜测成功率显著高于原始的PassGAN[15].
此外, Pasquini 等人[16]还提出了上下文Wasserstein 自编码器模型(context wasserstein autoencoder, CWAE)[75]用于条件性口令猜测(CPG),即掩码攻击场景(攻击者已知了用户口令的部分信息, 如长度、部分字符).在该场景下, 攻击者可利用口令模板(如**mm*91) 来生成一系列具有相似结构的口令簇(如summy91, tommy91 等).这些口令的表征向量在潜在空间(latent space) 彼此接近, 该特性也被作者称为强局部性(strong locality).与之对应的是, 不同数据集的分布之间呈现出一些更为通用的特征差异, 如不同口令策略导致的不同平均口令长度和字符组成, 这使得来自同一个(数据集) 分布的口令往往在潜在空间中更为集中, 这种特性被作者称为弱局部性(weak locality).
在此基础上, 作者进一步提出了动态口令猜测(dynamic password guessing, DPG) 技术.其核心思想是将成功猜测的口令持续地用于更新潜在分布, 并模拟未知的目标口令分布.具体而言, 给定目标口令集, 在使用生成器(在此使用GAN 的效果略好于CWAE) 生成猜测的过程中, 不断统计成功猜测的口令比例, 当超过某个阈值α后, 使用成功猜测的口令集动态调整/更新潜在分布.这种动态攻击策略尤其适用于跨站猜测场景, 即训练集与攻击目标来源于不同分布或分布差异较大.
随后的研究中, 研究者提出了一系列基于生成式模型的口令猜测方法.例如, 在2022 年, Yang 等人[76]提出了一种轻量级口令猜测模型VAEPass, 该模型基于变分自编码器.相较于PassGAN[15],VAEPass 具有较小的参数规模和更快的模型训练速度,同时在猜测成功率方面优于PassGAN.此外,Pagnotta 等人[77]提出了名为PassFlow 的基于流的生成式模型用于口令猜测.基于流的模型可以进行精确的对数似然计算和优化, 从而实现了准确的潜在变量推断.作者通过实验证明, PassFlow 的猜测成功率优于Pasquini 等人提出的基于GAN 的方法.
3.3.3 基于Seq2Seq 的口令重用模型Pass2Path
2019 年, Pal 等人[31]对用户的口令重用行为进行建模, 提出了一个基于序列到序列模型(Seq2Seq)的口令重用模型Pass2Path.他们的方法首先将用户的旧口令和新口令序列分别作为模型的输入和输出,旨在捕捉用户的口令重用模式.然而, 这种训练方法存在一个问题: 用户的新旧口令通常非常相似, 可能包含许多相同的字符或字符串.因此, 模型可能会学习到许多低效的“复制” 操作, 导致其在实际应用中的泛化能力较差.为了解决这一问题, 作者采取了新的策略, 将用户修改口令的行为视为一系列原子编辑操作.这些原子操作包括增加、删除和替换单个位置的字符.在此基础上, 作者将模型的输出调整为从旧口令到新口令的编辑操作序列.举例来说, 如果从口令wang123 变换为wang1!, 对应的原子操作序列为[(在索引为5 的位置删除字符2), (在索引为6 的位置删除字符3), (在索引为7 的位置插入字符!), 结束], 模型的输入为原始口令wang123 的字符序列, 输出为对应的原子操作序列.这一新的建模方式极大地提升了模型的猜测成功率.图6 为Pass2Path 模型的示意图.

图6 基于编辑操作序列的口令重用模型Pass2PathFigure 6 Password reuse model Pass2Path based on editing operation sequence
3.3.4 基于多步决策机制的口令重用模型Pass2Edit
2023 年, Wang 等人[35]指出如果将用户的口令修改过程建模为一系列原子修改操作(例如, 删除或插入特定的口令字符), 并使用神经网络来预测修改操作序列, 那么每个修改操作可能对后续的修改操作产生一定的影响.然而, 现有方法(如3.3.3 节所介绍的Pass2Path[31]) 无法准确学习到单个修改操作对当前口令的作用效果.为了更准确地表示用户的口令修改/重用行为, Wang 等人首次将口令重用攻击建模为一个多分类问题, 并提出了一个名为Pass2Edit 的生成模型.该模型采用多步决策机制, 能够在口令经历复杂变换时学习到修改操作对当前口令的作用效果.
具体而言, Pass2Edit 模型的输入由原始口令和之前单个修改步骤所产生的当前口令共同组成.模型的输出是下一步的原子修改操作.在输出单步修改操作后, 模型将该修改操作应用到输入端的当前口令中,作为下一步的模型输入.如此循环迭代, 直至输出终止操作.通过这种多步决策学习机制, 模型能够学习到口令修改过程中每个修改操作对原始口令的影响.例如, 假设原始口令为wang123, 目标口令为wang1!,那么这两个口令之间的编辑操作序列为[(在索引为5 的位置删除字符2), (在索引为6 的位置删除字符3), (在索引为7 的位置插入字符!), 结束].神经网络的输入涵盖了原始口令以及当前已修改的口令, 而输出则是下一步的单步编辑操作.首先, 将两个原始口令作为模型的输入, 第一步输出为(在索引为5 的位置删除字符2); 然后, 将该操作应用于原始口令wang123, 得到当前修改后的口令wang13, 并将其与原始口令一同作为下一步的模型输入, 输出为(在索引为6 的位置删除字符3); 再依照同样的方式, 循环调用该网络, 直至遇到结束操作.图7 为该方法的一个示例说明.
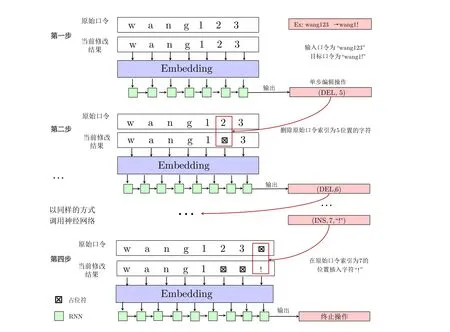
图7 基于多步决策机制的口令重用模型Pass2Edit [35]Figure 7 Password reuse model Pass2Edit based on multi-step decision-making mechanism [35]
3.3.5 基于规则的自适应攻击算法ADaMs
基于规则的字典攻击通常由两个关键组成部分构成: 一个包含n个口令的基础字典集及一个包含m个变换规则的规则集.在生成猜测时, 会将规则集中的每个规则变换应用于基础字典中的每个口令, 从而生成n×m个口令作为猜测字典.然而, 这种方法会导致大量无效或重复的猜测, 因为在现实世界中, 不同基础口令与不同规则的适配程度存在巨大的差异.举例来说, 长度较短的口令相对于长度较长的口令更适于被应用在尾部添加字符(串) 的规则.类似地, 对于由纯小写字母构成的口令, 更适于应用全体字符大写的规则, 而对于由字母和数字混合构成的口令, 这种规则的适用性可能较低.
针对此问题, Pasquini 等人[24]在2021 年提出了一种新型字典攻击技术, 该技术无需监督或专业领域知识, 能够自动模拟真实攻击者采用的高级猜测策略, 在应对不完善的字典攻击配置方面表现出更强的适应性.具体而言, 对于给定基础字典W和规则集R, 通过引入一个足够大的字典X, 为基础字典中的每个口令wi和规则集中的每个规则rj分配一个类别标签: 标签为1 表示rj(wi)∈X, 0 表示rj(wi) /∈X.通过这种方式, 每个口令将被分配|R| 个标签(即规则的数量), 此时, 基础口令与规则的适配程度可视为一个多标签分类问题(multi-label classification).随后, 作者使用深度神经网络来学习规则集所对应的适配函数.模型训练完成后, 模型将对每个口令wi和每个规则rj输出一个位于0 到1 之间的适配分数, 其中接近1 的数值表示rj对wi是适配的.相反, 输出值接近0 表示真实情况下将rj应用于wi的概率极低.最后, 通过设置适配分数阈值来排除那些对给定口令无效的规则(例如, 设置阈值为0.5 即可排除85%/90% 的无效规则[24]), 从而大大提升了原始字典攻击的攻击效率.在此基础上, 他们引入了动态猜测策略, 即将每一个新猜出的口令都插入到原始基础字典中, 这在现实情况下对应了专家根据目标情况即时调整猜测策略的能力, 从而进一步提升了攻击效率.
3.3.6 Chunk-Level 口令猜测框架
2021 年, Xu 等人[33]指出现有口令猜测模型大多将口令视为连续的字符序列, 或假设不同类型字段之间相互独立, 这些方式均无法捕获口令中存在的独有模式, 如4ever、ing 等.针对此问题, Xu 等人通过引入字节对编码(byte-pair-encoding, BPE) 算法, 将口令划分为更细粒度的块级(chunk-level) 表征.例如, 口令p@ssw0rd4ever 可以通过BPE 划分为p@ssw0rd 和4ever 两块.使用BPE 算法将口令切分成chunk 的大体流程如图8 所示.

图8 使用BPE 算法将口令切分成chunk 表征[33]Figure 8 Use BPE algorithm to split password into chunk representation [33]
在此基础上,Xu 等人[33]构建了三个基于chunk 划分的口令猜测模型: Chunk-level Backoff、Chunklevel PCFG 和Chunk-level FLA.对于Chunk-level Backoff,它与普通Backoff[22]的区别在于使用chunk代替原始的单个字符作为计算转移概率的最小单元; 此外, Chunk-level Backoff 还限制了预测下个chunk所需考虑的最大chunk 前缀数目.其训练与生成过程与普通Backoff 类似.对于Chunk-level PCFG, 它在原有PCFG[21]大/小写字母U/L、数字D 和特殊符号S 的基础上, 额外引入了DM、TM 和FM 三种类型的标签, 分别代表两种类型字符混合的字符串(double mixed type, 如4ever 可表示为DM5)、三种类型字符混合的字符串(three mixed type, 如p@ssw0rd 可表示为TM8) 和四种类型字符混合的字符串(four mixed type, 如P@$$w0RD 可表示为FM8).其训练与生成过程也与普通PCFG 类似.对于chunklevel FLA, 它与普通FLA[14]的区别在于使用chunk 代替原始的单个字符, 模型通过先前的chunks 作为上下文环境来预测下个chunk 出现的概率.由于chunk 的种类远多于单个字符的种类, 作者使用了一个嵌入层来代替原始字符级FLA 所使用的独热编码层(one-hot encoding layer).其余过程和普通FLA类似.作者通过实验证实, 三个chunk-level 模型的猜测成功率均优于对应的原始模型.
3.3.7 基于随机森林的口令猜测框架RFGuess
2023 年, Wang 等人[26]以随机森林算法为例, 通过对口令字符的重新编码, 设计了基于经典机器学习技术的新型口令猜测框架RFGuess, 涵盖漫步猜测场景和两个定向猜测场景(即, 基于个人信息的定向猜测和基于口令重用的定向猜测).
首先介绍漫步口令猜测算法RFGuess.给定一个口令(如password), 将该口令每个字符前面的n阶字符串作为分类目标(如passwo), 而将该字符(如passwo 所对应的字符r) 作为对应待分类字符串的正确分类标签.其中,n阶字符串中的每个字符使用[字符类型(即, 数字, 小写/大写字母, 特殊符号), 字符所在类型序号(如, 字母a 位于a–z 序列的第一个), 字符所在键盘行号, 字符所在键盘列号] 四个维度来表示,n阶字符串整体再使用[已遍历的字符长度, 当前字符所在的相同字符类型的段已经遍历长度] 两个维度来表示, 共计4n+2 个维度.下面给出一个具体示例.
以口令qwer654321 为例, 取其6 位前缀wer654.首先, 可以将wer654 中的每个字符用一个4 维特征向量进行唯一表示.例如, 字符r 被表示为[3, 18, 2, 4], 其中3 表示小写字母, 18 是r 在小写字母序列a–z 中的排名, 2 和4 分别是r 在键盘上的行和列位置.如此, wer654 可以由一个24 维特征向量表示(24 = 4×6).然后, 添加一个2 维向量[7, 3] 来表示前缀wer654 的长度特征, 其中7 表示数字4 是qwer654321 的第7 个字符, 3 表示数字4 是数字段654321 的第3 个字符).在训练阶段, 将训练集中的所有口令转化为n阶字符串的形式.模型的输入是每个n阶字符串的向量表示, 而输出则是与该字符串对应的字符标签.生成猜测的过程类似于Markov 模型.从一个n阶起始字符串开始, 模型逐个字符地生成, 直到遇到终止符.该过程可视为模型通过观察之前的字符来预测下一个字符, 以此生成可能的口令猜测.图9 为使用决策树对口令前缀进行分类的简单示例.
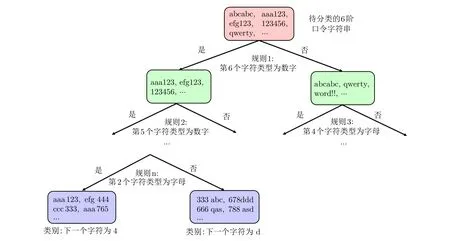
图9 使用决策树对n 阶口令字符串进行分类[26]Figure 9 Classify n-order password strings using decision trees [26]
基于个人信息的定向口令猜测算法RFGuess-PII 与漫步算法RFGuess 原理相同, 不同之处在于对包含个人信息口令片段的编码方式不同.具体来说, 对于定向算法, 个人信息的使用行为除了没有键盘特征外, 其他与普通字符相似.首先, 个人信息也有不同类型之分(如邮箱、用户名、姓名等, 这类比于普通字符的字符类型), 而且不同类型个人信息之间的使用行为也互不相关.其次, 给定个人信息类型, 其使用行为也有着一定的规律/关联性(如姓名包含姓名全称、姓名缩写、姓氏等一系列变型, 这可类比于普通字符的字符序号).因此, 使用[个人信息类型, 个人信息行为序号, 0, 0] 这四个维度表示定向猜测算法中包含个人信息的片段特征, 其中, 最后两个0 是为了与普通字符的特征对齐.以口令wang123 为例, 个人信息片段wang 可表示为(10, 1001, 0, 0), 其中10 代表姓名这一个人信息种类, 1001 代表使用姓名信息的第一种变型, 即姓氏.该算法的训练和猜测生成过程也与RFGuess 相似.
基于口令重用的定向口令猜测算法RFGuess-Reuse 可分为两个主要阶段: 结构级变换和字段级变换.在结构级变换阶段, 统计训练集中所有口令对在结构层面的转换操作及对应频率.例如, 统计从结构L8S2(表示长度为8 的字母片段和长度为2 的特殊字符片段) 变化为结构L7D3(表示长度为7 的字母片段和长度为3 的数字片段) 的口令对的频率, 并依据概率进行排序.接下来, 在字段级变换阶段, 使用随机森林算法对字段级转换操作进行预测.例如, 在字母片段中, 若将password 转换为passwor, 那么随机森林的作用是输入password, 然后预测应该采取的编辑操作, 即删除最后一个字符d.以下给出一个完整的示例.给定一个口令password!!, 生成目标口令p@sswor123 的概率计算过程为Pr(password!!→p@sswor123) = Pr(password!!→password)× Pr(password→passwor)×Pr(passwor→passwor123)×Pr(passwor123→p@sswor123)×p4,其中,Pr(password!!→password) (即 L8S2→L8) 和 Pr(passwor→passwor123) (即 L7→L7D3) 表示结构级转换的概率, 可以通过训练集中口令对的统计数据获得; Pr(password →passwor)(即删除单个字符d) 和Pr(passwor123 →p@sswor123)(即a →@) 是字段级转换的概率, 可以通过已训练的随机森林模型获得;p4是经过四次转换后结束的概率, 同样可以通过训练集的统计数据获得.
3.3.8 基于双向Transformer 的口令猜测框架PassBERT
2023 年, Xu 等人[32]将自然语言处理领域的预训练/微调技术用于口令猜测, 提出了一个基于双向Transformer 的口令猜测框架PassBERT.该框架涵盖三种不同类型的攻击场景: (1) 基于部分口令信息的掩码攻击场景(即攻击者已知了用户口令的部分信息, 如长度和/部分字符); (2) 基于口令重用的定向攻击场景; (3) 基于规则的自适应攻击场景.具体来说, 作者首先使用大规模口令数据集(Rockyou-2021), 基于掩码语言建模(masked language modeling), 建立了口令预训练模型.其中, 掩码语言建模是指, 训练模型使其能利用包含掩码字符的口令模板(如il*v*u4*ve*) 来恢复出该模板所对应的原始完整口令(即iloveu4ever).在此之后, 作者根据三种攻击场景的不同特点, 对预训练模型进行了针对性微调, 即为三种攻击场景设置了不同的监督信号(supervision signals).
具体来说, 掩码攻击模型的输入为口令模板(与预训练的不同之处在于, 将原始BERT 模型的15%字符掩盖比例提升为50%), 输出为完整的原始口令; 定向攻击模型的输入为旧口令的字符序列, 输出为从旧口令到新口令的最短编辑操作序列(作者定义了三种不同的操作, 分别为保持不变、删除和单个/双个字符替换); 自适应攻击模型的输入为口令字符序列, 输出为针对所选规则集中的每个规则与该口令匹配程度的一个数值(位于0 到1 之间).PassBERT 的整体框架如图10 所示.作者通过实验证实, 所提出的三个模型的猜测成功率均优于对应场景下最先进的口令模型.

图10 PassBERT 的整体框架[32]Figure 10 Overview of PassBERT framework [32]
4 口令猜测算法评估
4.1 口令猜测算法评价指标

在现实世界中, 网站或服务器为了防御口令猜测攻击, 会采用加盐(对抗预计算技术, 如彩虹表)、增加Hash 次数、使用内存困难函数(MHF) 等安全防御措施, 这会大大提高攻击者单次猜测的成本, 而该成本与系统环境和攻击者的硬件计算能力息息相关.因此, 在评估猜测算法的实用性时, 算法的计算效率理应成为猜测算法的评价指标之一.具体来说, 算法的计算效率主要体现在训练时间、运行所需要的硬件支持(是否需要GPU、占用内存大小等)、模型大小以及口令生成速度.此外, 尽管不断泄露的口令文件为攻击者提供了丰富的资源, 但仍存在大量训练数据资源匮乏的攻击场景(如银行和除了中、美、俄以外的其它国家/地区).因此, 算法充分发挥性能所需要的训练集大小也应纳入考虑范围.
4.2 口令猜测场景
口令猜测场景可以根据不同的标准进行分类, 包括是否使用目标的个人信息(如姓名、生日、邮箱、用户名等)、是否与服务器交互、允许的猜测次数的大小等.
根据是否使用目标的个人信息, 口令猜测攻击可分为漫步猜测与定向猜测.所谓漫步猜测, 是指攻击者不关心攻击的具体目标, 其目的是破解出尽可能多的口令; 所谓定向猜测, 是指攻击者利用与目标相关的各种信息(如姓名、邮箱、已泄露的旧口令等), 其目的是尽快破解出指定目标的口令.根据攻击者所拥有目标信息的不同, 本文将定向猜测场景进一步分为基于个人信息(如姓名、邮箱、生日、用户名等个人信息) 的定向猜测和基于口令重用的定向猜测.在定向猜测场景下, 指标猜测成功率的计算方法如下: 为测试集中的每个用户生成一定数量的猜测集, 然后统计测试集中所有用户在其对应猜测集下的破解情况.例如, 定向猜测算法A在100 猜测数下猜测成功率为20% 表示: 对于测试集中的所有用户, 有20% 用户的口令在其对应猜测集的前100 次猜测内被成功破解.
根据是否与服务器交互, 口令猜测攻击可分为在线猜测与离线猜测.在线猜测往往难以避免: 任何拥有浏览器的人都可以对公开界面的服务器发起基本的在线猜测攻击.为了抵御在线攻击, 服务器往往被建议部署登录速率限制机制(rate-limiting), 如账户锁定(account lockout) 和登录节流(login throttling).然而, 现实情况却不尽人意.Lu 等人[78]在2018 年的研究表明, 约72% 的网站(131/182) 允许频繁的、不成功的登录尝试, 而没有账户锁定或登录节流措施.对于这些网站, 攻击者每天可以进行超过85 次的登录尝试, 这远超过NIST-800-63-3 所建议的30 天内每个账户允许的错误口令登录次数不应超过100[79].事实上, 即使是采取了严格速率限制机制的网站, 其每月允许的错误口令登录次数也远超过100.例如, 亚马逊网站的速率限制机制为每小时允许连续五次错误登录尝试, 据此推算, 攻击者每天可至多进行120 次登录尝试, 每个月可进行3600 次登录尝试.与之对应的是, 在现有研究中(如文献[26,28,56,80,81]), 在线猜测算法的最大猜测数通常设置为103∼104.
离线猜测需要攻击者能够获取服务器泄露的口令文件, 可尝试的猜测次数仅仅受限于攻击者本身的计算资源和愿意投入的成本.Florêncio 等人[80]指出, 离线猜测攻击只在非常受限的情形下才构成现实威胁: 服务器端采用了正确的口令加盐hash 方法, 口令文件被泄露且未被察觉.对于猜测算法的评估来说, 在线猜测与离线猜测的本质区别在于猜测次数的大小不同.Florêncio 等人[80]通过分析指出,1014可以作为离线猜测的一个下界.然而, 现有研究中(如文献[16,21,22,52]), 受计算资源的限制, 几乎所有的猜测算法在被评估时, 实际生成猜测数的最大数量级为1012(见文献[24] 的图8), 一般数量级在107∼1010[16,21–23,52], 尚未见实际生成超过1013的猜测算法研究.
4.3 蒙特卡洛采样方法
对于算法在大猜测数的表现, 通常采用蒙特卡洛采样方法进行评估[30].蒙特卡洛采样的基本原理是,基于猜测模型所定义的口令分布随机抽样, 通过样本口令的概率和测试集中每个口令在猜测模型下的概率, 估计测试集中每个口令的强度(即, 被攻破所需的猜测数), 最终得到该模型在对应测试集下的猜测成功率曲线.该方法只适用于概率模型(即猜测模型所对应的口令空间的概率加和为1.0).
以Markov 模型[22]为例(记为p), 假设我们的字符表包括95 个可打印字符和一个终止符.在训练完成后, 模型逐个字符生成样本口令, 具体流程为: 每个字符都被模型p分配一个概率值, 表示该字符作为生成口令首个字符的概率; 将0 到1 这个区间划分成96 个小区间, 每个区间代表一个字符以及该字符所对应的概率范围; 在生成口令时, 使用一个随机种子生成一个0 到1 之间的随机概率, 然后确定它位于这96 个小区间中的哪一个, 从而选择相应的字符作为模型生成口令的首个字符, 记为c1; 接下来以同样的方式生成该口令的第二个字符, 此时, 字符表中的每个字符会被模型分配一个新的概率, 表示该字符出现在c1之后的概率; 重复该抽样过程, 将抽取的字符依次添加至当前字符串并记录其对应的随机数, 直到抽取到终止字符为止.这样就完成了一个口令样本的采样, 而其采样概率可以通过将所有采样字符对应的随机数相乘来得到.重复此过程, 生成大小为n的样本集, 记作Θ, 每个生成的口令样本记为β, 其对应的生成概率用p(β) 表示.随后, 计算测试集中的每个口令(记为α) 在模型p下的概率, 记为p(α).再依据以下公式对口令α的猜测数进行估算:

2023 年, Liu 等人[82]注意到Dell’Amico 等人的蒙特卡洛估计方法没有提供关于猜测数范围的统计置信区间, 也明确指出存在高度不确定性的情况.基于这一发现, 他们提出了自信蒙特卡洛评估, 该方法在给定置信度时, 能够提供猜测曲线(即猜测成功率vs.猜测数) 的上下界, 进一步增强了原始蒙特卡洛估计方法的科学性和完整性.在第4.4 节中, 将从实验的角度证实蒙特卡洛估计方法的有效性.
4.4 实验设置与算法评估
科学的实验设置对于公平评估口令猜测算法的表现至关重要.如本节所示, 不同算法通常在不同的猜测场景中表现出优势.以往的研究表明, FLA 算法在大规模猜测数(如>1010) 的情况下相对于PCFG 和Markov 算法表现出了明显的优势[14], 而RFGuess 算法则在小规模训练集(如1 万训练集) 和同站测试场景下优于其他方法[26].为了确保对不同算法的评估具有准确性、公平性和合理性, 本文首先设计了一系列通用猜测场景, 以观察各算法在不同条件下的猜测成功率.在此基础上, 考虑到不同算法的潜在优势,根据各算法的原始文献, 设置了特定的实验场景, 以展示它们在自身擅长领域的性能.这种兼顾通用性和定制化的实验场景设计确保了对各算法能力的全面评估, 有助于更好地理解它们的应用范围和局限性.
4.4.1 漫步攻击场景
漫步猜测场景的实验设置如表9 所示.在场景 #1∼#6 中, 分别选取 50%、30% 和 10% 的Dodonew/000Webhost 数据作为训练集, 以研究模型对训练集规模的敏感性.对于测试集, 首先, 使用20% 的Dodonew/000Webhost 数据创建基础测试集, 模拟同站猜测场景(场景#10 和场景#15).接着, 从这20% 的Dodonew/000Webhost 数据中随机抽取不同规模的子测试集(1 万、10 万和100 万个口令, 对应场景#7∼#9 和场景#13∼#15), 以观察测试集规模对实验结果的影响.同时, 排除20%Dodonew/000Webhost 中在训练集中已经出现过的口令, 以评估模型生成新口令的能力, 即泛化能力(对应场景#11 和场景#17).最后, 使用随机选取的100 万条Taobao 和Wishbone 数据集作为测试集, 以模拟跨站猜测场景(场景#12 和场景#18).值得注意的是, 000Webhost 要求口令长度大于6, 且至少包含一个数字和字母, 因此还进一步对数据集Wishbone 按照000Webhost 的口令策略进行过滤, 以观察口令策略对实验结果的影响(场景#19).

表9 漫步猜测场景实验设置Table 9 Experimental setup of trawling guessing scenarios
本文对比了几种具有代表性的口令猜测方法, 包括PCFG/PCFGv4.1[21]、Markov[22]、Backoff[22]、FLA[14]、DPG[16]、RFGuess[26]、ADaMs[24]和PassBERT(-ARPG)[32].模型参数遵循原始论文的最佳推荐.针对概率模型(PCFG、Markov、Backoff、FLA 和RFGuess), 根据各自的训练/生成速度和内存消耗(见表10), 实际生成了不同数量级的猜测数, 并与相应的蒙特卡洛评估结果进行了对比(场景#12和#18).对于DPG, 使用80% 000Webhost/Dodonew 作为训练集, 以剩下20% 数据集作为攻击目标,生成了约109个猜测.而对于ADaMs 和PassBERT(-ARPG), 其训练过程通常需要一个基础字典、一个规则集和一个大规模目标集, 本文采用作者提供的预训练模型和规则, 将80% 000Webhost/Dodonew 用作基础字典, 实际生成了约109个猜测.详细情况如表9 所示.

表10 不同漫步猜测模型的计算效率†Table 10 Performance of different trawling guessing models
图11(a)、图11(b)、图11(d)和图11(e)为所有方法的对比结果.整体看来,在不去除训练集与测试集交叉部分的同站猜测场景中(即图11(a)和图11(d)),概率模型(如Backoff[22]、FLA[14]和RFGuess[26])的猜测成功率通常优于基于规则的方法(如ADaMs[24]和ARPG[32].这里需要注意的是, 图11(a)、图11(b)、图11(d)和图11(e)中的“_pwdpro” 和“_generated” 分别代表使用两种不同的规则集所训练的模型), 这些结果说明概率模型能更有效地拟合训练集口令分布.值得注意的是, 从104猜测数开始,DPG[16]在英文数据集(见图11(d)) 的猜测成功率逐渐优于其它方法.原因在于DPG 在该猜测数下, 启动了动态调整机制, 将成功猜测的口令用于调整/更新潜在分布.正因如此, 在去除测试集中在训练集中出现过的口令后(即图11(b)和图11(e)), DPG[16]表现尤为出色.而其余各个方法的猜测成功率均显著下降, 在10 万猜测数内, 猜测成功率几乎为0, 且彼此相差不大.对于字符级自回归模型(即Markov[22]、Backoff[22]、FLA[14]和RFGuess[26]), Backoff、FLA 和RFGuess 由于在不同程度上缓解了Markov模型存在的数据稀疏和过拟合问题, 猜测成功率通常大于等于Markov.

图11 漫步猜测实验结果图(∗表示去除了测试集中在训练集中出现过的口令)Figure 11 Trawling guessing scenarios (∗means removing passwords seen in training set from test set)
表10 列出了几个主要模型的训练时间、模型大小和口令生成速度.各模型在不同场景的运行特性决定了各自的适用性.例如, 训练时间相对较短的模型(如RFGuess[26]) 更适用于在线猜测场景; 模型大小较小的模型(如FLA[14]) 更适合用于客户端层面的口令强度评估(client-side PSM); 而生成速度较快的模型(如PCFG[21]) 更适用于大规模离线口令猜测任务.值得注意的是, 在不断涌现各种口令猜测算法的今日, 综合考虑模型的训练/生成速度和猜测成功率, PCFG[21]仍表现卓越.
图11(c)和图11(f)为PCFG[21]、Markov[22]、Backoff[22]和FLA[14]利用实际生成的猜测集与使用蒙特卡洛估计[30]所得到的“猜测数vs.猜测成功率” 曲线.观察发现, 每种方法对应的两条曲线几乎重合.这从实验的角度证明了蒙特卡洛估计方法在给定猜测数下的准确性.
不同方法在不同测试集大小下的实验结果如图12 所示.观察发现, 测试集大小从1 万变化至>100万时, 各个方法的结果几乎一致(猜测成功率误差<1%).这表明, 一旦测试集大小超过1 万, 不同方法的猜测成功率就会趋于稳定, 这与文献[30] 中推荐的测试集大小一致.
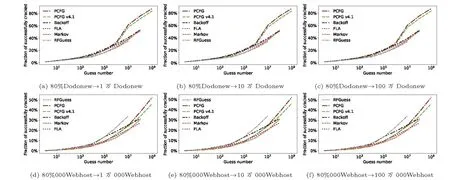
图12 漫步猜测实验结果图(测试集大小对实验结果的影响)Figure 12 Experimental results of trawling guessing (Impact of testing set size on experimental results)
不同方法使用不同大小训练集的实验结果如图13 所示.观察发现, RFGuess[26]在训练集较小的情况下(如使用10%Dodonew/10%000Webhost 和30%000Webhost 作为训练集), 效果通常略优于其他方法, 这与文献[26] 的结论一致.随着训练集大小的增大, 不同方法的猜测成功率有不同程度的提高1我们使用FLA 源码, 分别使用原始论文中推荐的“大模型” (隐藏层单元为1000) 和“小模型” (隐藏层单元为200) 参数重复了多次实验, 发现“小模型” 的结果略优于“大模型”, 一个可能的原因是, 50%Dodonew 作为训练集的数据量不足..其中,PCFG 的猜测成功率变化最大, 原因在于, PCFG 在生成猜测时, 结构段的填充内容(如S3→!!!) 均来自训练集, 较小的训练集无法提供足够的填充片段.
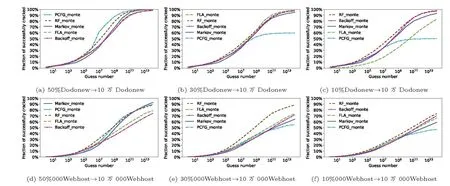
图13 漫步猜测实验结果图(训练集大小对不同方法的影响)Figure 13 Experimental results of trawling guessing (Impact of training set size on different methods)
此外, RFGuess[26]在使用大规模数据集训练和生成口令时, 会占用大量的内存(如使用500 万训练集约占用40–80 GB, 原因在于RFGuess 在运行时会将所有字符前缀数据同时读入内存), 且生成速度较慢(每秒可生成130 个口令; 见表10), 这使得该方法更适用于训练数据资源相对匮乏(如和银行相关的口令数据) 和对生成速度要求不高的在线猜测场景.
口令策略对不同方法的影响如图14 所示.观察发现, 同一测试集, 口令策略不同, 攻破率也不同.例如, Backoff[22]在不经口令策略筛选的测试集上, 效果优于其他方法, 而在筛选之后, 猜测成功率与其他方法差异不大.这表明, 在对口令猜测方法进行评估与对比时, 考虑训练集与测试集口令策略的一致性是很有必要的.尽我们所知, 当前尚未有研究通过具体的实验探究过该问题.

图14 漫步猜测实验结果图(口令策略对不同方法结果的影响)Figure 14 Experimental results of trawling guessing (Impact of password policy on different methods)
4.4.2 基于个人信息的定向攻击场景
对于基于个人信息的定向猜测场景, 考虑到包含个人信息的数据集通常规模不大, 我们没有采用不同比例的划分方法, 而是遵循了之前在定向猜测研究中最常见的划分方式, 即将50% 用于训练, 剩下的50%用于测试.Wang 等人[27]指出, 这种划分方式是合理的, 原因如下: 首先, 聪明的攻击者会不断改进他们的训练集, 使其分布尽可能与测试集接近.例如, 攻击者可能会选择与攻击目标具有相同语言、服务类型和口令策略的数据集来进行训练.而这种一半对一半的划分方式正好模拟了这种理想的攻击场景.其次,这种做法并不违反机器学习的原则, 即训练集和测试集应该不同.根据口令服从Zipf 分布的特性[49,57],50% 用于训练的口令中会有相当一部分不会出现在剩余50% 的测试口令中.比如, 随机将Dodonew 等分为两半(记为训练集Dodonew-tr 和测试集Dodonew-ts), Dodonew-tr 中81.22% 的口令没有出现在Dodonew-ts 中.这一法则确保了训练集和测试集相似但不相同.事实上, 许多网站的口令泄露情况发生过多次, 如Yahoo[83]、Flipboard[84]、Twitter[85]和Anthem[86]等.
本文对三种最具代表性的基于个人信息的定向口令猜测算法进行了比较, 这些算法包括TarGuess-I[28]、Targeted-Markov[60]和RFGuess-PII[26], 同时考虑了同站和跨站猜测场景(实验设置详见表11).实验结果如图15 所示.总体而言, 这三种定向猜测算法的攻破率差距不大, 其中, RFGuess-PII 略微优于其他两种方法, 这与之前研究[26]的实验结果一致.

图15 基于个人信息的定向口令猜测场景Figure 15 Targeted password guessing scenarios based on personal information

表11 定向猜测攻击场景设置Table 11 Experimental setup of targeted guessing scenarios
4.4.3 基于口令重用的定向攻击场景
对于口令重用攻击, 本文重现了文献[35] 中的三个场景(即对应表11 中的场景#5–#7), 对比了当前最先进的几种口令重用算法, 即TarGuess-II[28]、Pass2Path[31]、PassBERT[32]以及Pass2Edit[35].其中, TarGuess-II 和Pass2Edit 还使用了额外的流行口令字典(预先使用3 个数据集进行混合, 取频率相乘后排名靠前的Top-10000 口令; 详见文献[35] 的4.3 节), 即在生成的重用口令中混入流行口令, 来模拟用户在创建新口令时选择流行口令的脆弱行为.为了更公平地对比, 对Pass2Path 和PassBERT 也采用同样的流行字典进行混合, 混合方式为模型生成的重用口令: 流行口令= 2 : 1 (该比例为实验测试的最佳比例).同时, 为了排除混合方法不同带来的偏差, 还去除了TarGuess-II 和Pass2Edit 所使用的流行字典, 即Pass2Edit-nomix 和TarGuess-II-nomix.
根据图16 和文献[35] 的结果, 在1000 猜测数下, Pass2Edit(或Pass2Edit-nomix)[35]的猜测成功率高于其他方法.在英文数据集上, PassBERT[32]和PassBERT-mix[32]在小猜测数(<10) 下表现出了更好的猜测效果, 明显优于TarGuess-II[28]和Pass2Path[31].随着猜测次数的增加, PassBERT 和PassBERT-mix 的攻破率逐渐与TarGuess-II 趋于持平.而在中文数据集上, Pass2Path 在引入流行口令混合后(即Pass2Path-mix), 其猜测效果明显超过了TarGuess-II 和PassBERT.在混合数据集上, 除了Pass2Edit 之外, 其他方法的攻破率相对均衡, 没有明显的差异.

图16 口令重用攻击场景Figure 16 Targeted password guessing scenarios based on password reuse
此外, 本文还统计了不同方法的训练时间、模型大小和口令生成速度, 如表12 所示, 发现TarGuess-II[28]的训练速度最快, PassBERT[32]的生成速度最快(需要GPU 支持), Pass2Edit[35]的模型体积最小.因此, 在实际应用时, 可优先尝试Pass2Edit 及其变种, 但对于特定的数据集和猜测需求, 可以考虑其他方法以获取最佳性能.例如, 口令泄露检测服务(支持口令变体泄露查询, 如文献[87]) 每天通常会处理数百万用户的查询请求, 需要生成数以亿计的口令变体, 因而可能对算法的生成速度要求更高.

表12 各个口令重用模型的计算效率†Table 12 Performance of different reuse models
5 口令猜测算法应用
近年来, 涌现了大量口令猜测算法[16,24,26,32,35], 这些算法的应用主要集中在防御者的视角, 特别是更准确地建模口令的抗猜测性(guessability).本节将深入探讨口令猜测算法在口令强度评估、数字取证以及口令泄露检测等领域的实际应用, 同时也将探讨它们所面临的挑战和问题.
5.1 口令强度评估
了解最先进的攻击技术对于设计最佳的防御策略至关重要.口令作为许多安全系统的第一道防线甚至是唯一一道防线, 其强度直接影响着系统的安全性.因此, 对口令强度进行准确评估尤为重要, 而口令猜测算法的一个核心应用即是从攻击者的视角准确评估口令强度.当前, 已有一系列基于猜测算法的口令强度评价器(PSM), 如FLA-PSM[14]、fuzzyPSM[88]、CNN-PSM[89]、chunk_level-PSM[33]等; 此外, 还有基于定向猜测算法的PSM, 如PPSM[31].然而, 出乎意料的是, 截至目前, 基于猜测算法的PSM 均未在实际系统中得到广泛应用.一个主要原因在于, 口令的强度不仅受口令本身复杂性的影响, 还受攻击者所掌握的信息影响.因此, 要准确评估口令的强度, 需要考虑多种不同情境, 使用单一的PSM 无法实现.例如, 基于漫步猜测算法的PSM 可能无法准确评估包含个人信息的口令的强度; 攻击者如果已经掌握了用户的旧口令, 那么该用户创建的新口令的强度也会受到影响.如何以科学合理的方式充分利用各种猜测算法来准确评估用户口令的强度, 仍然是一个需要深入研究的问题.
5.2 数字取证
当前, 许多电子设备(如手机和个人电脑) 都使用口令作为安全保护手段, 由此带来的设备解锁问题已成为数字取证工作中最为严峻的挑战之一[90].若无法及时获取犯罪嫌疑人的口令, 可能会延缓调查进程,甚至可能导致更多犯罪行为的发生.幸运的是, 现有的口令猜测算法为执法机构破解加密设备/材料提供了一种潜在的途径, 帮助加速数字取证工作的进展.例如, 执法人员可以通过收集开源情报(OSINT) 来获取与目标相关的个人信息, 再将这些个人信息与猜测算法相结合, 可以显著提高执法机构解锁设备的效率,进而为数字取证工作提供重要线索.
5.3 口令泄露检测
口令泄露检测主要分为用户和服务器两个层面.在用户层面, 用户可以使用口令检测服务(例如“Pwned Passwords”[91]) 来查询自己的口令是否已经泄露.考虑到有26%∼33% 的用户在创建口令时会对已有口令做出简单的修改[3], 泄露检测服务还应具备检测用户相似口令是否曾经泄露的功能.确保这一功能的关键是准确测量口令之间的相似性, 以便判断哪些口令可能是用户查询口令的变体[87].虽然有一系列用于测量字符串相似度的指标(例如基于编辑距离的指标和基于余弦相似度的指标[56]), 但它们都无法准确地建模用户的口令重用和修改行为.因此, 一种直观的方法是从攻击者的角度出发, 利用口令重用模型/算法来根据用户输入的查询口令生成相似的变体, 然后结合一定的字符串相似度指标, 为用户提供更全面准确的口令泄露查询服务.
在服务器层面, 口令猜测算法可用于生成诱饵口令, 来达到口令文件泄露检测的目的[27,34,92].所谓诱饵口令, 是指服务器为每个用户的真实口令生成一系列(k −1 个) “假口令”, 与用户的真实口令存储在一起, 达到以假乱真的目的.如此一来, 一旦口令文件发生泄露, 即使攻击者能恢复出全部口令, 仍需要从每个用户的k个口令中分辨出哪个是真实口令.为此, 攻击者需要进行在线登录尝试, 一旦系统检测到有一定数量的假口令在尝试登录, 即表明口令文件可能已经发生泄露.整个流程的关键在于, 能否生成以假乱真的诱饵口令.Wang 等人[34]的研究表明, 理想诱饵口令的分布应与用户真实口令的分布一致, 而组合多种不同类型的口令猜测算法被作者证明是行之有效的方法之一.
尽管Honeywords 技术已被提出多年, 且有一系列相关研究[27,34,92,93].但截至目前, 尚未有网站实际部署了此类系统.可能原因如下: (1) Honeywords 系统很容易受到拒绝服务攻击(DOS).具体而言, 如果诱饵口令与用户真实口令的分布几乎一致, 会出现大量的流行诱饵口令, 攻击者很容易利用这些特征对网站发起DOS 攻击, 引发系统误报.(2) Honeywords 系统需要把用户正确口令索引相关的信息存储在一个单独的、固化的、极简设计的计算机系统上, 并假设该系统是绝对安全的.这既不现实, 也需要网站增加额外的部署设备, 并对现有系统进行相应的调整.
6 总结与展望
当前, 虽然无口令方案崭露头角(如Passwordless[94]), 用户可能减少对口令的直接接触, 但口令在可预见的未来仍将是最主要的身份认证手段, 无可替代[8].因此, 口令将继续作为保障数十亿网民和信息系统安全的第一道防线, 口令猜测算法的研究对建立可持续的口令安全生态至关重要.本文系统性总结了当前国内外的主要口令猜测算法, 并指出了存在的不足和值得进一步研究的方向.下面探讨口令猜测未来的研究需求.
6.1 掩码猜测研究
在IEEE S&P ’21 中, Pasquini 等人[16]提出了条件口令猜测(conditional password guessing) 的概念(即掩码攻击).它是指攻击者通过各种攻击手段(如肩窥、键盘敲击回声等侧信道攻击) 获取了用户口令的部分信息(如口令长度和/或部分口令字符), 然后利用口令模板(如**mm*91) 来帮助生成更有效的猜测集.在USENIX SEC ’23 中, Xu 等人[32]针对此场景提出了更有效的PassBERT 模型.然而, 他们都没对掩码场景的现实性和危害性进行系统的讨论.例如, 攻击者能通过哪些方式获取用户口令的哪些部分信息?口令部分信息泄露会造成多大的危害?当前, 尚未有关于掩码猜测场景的系统研究.
6.2 多口令猜测研究
在IEEE S&P’19 中, Pal 等人[31]指出了一个有趣的现象: 通过将同一用户的两个旧口令输入到口令重用模型Pass2Path 中, 然后合并生成的猜测集, 可以有效提高模型对同一用户新口令的猜测成功率.然而, 这种方法并没有充分考虑到旧口令之间的内在联系.此外, 研究作者并未提供一种有效的猜测混合顺序, 即在给定猜测次数的情况下, 如何对多个口令模型生成的猜测进行排序.另一方面, 当尝试使用同一用户的多个旧口令来辅助猜测其目标口令时, 可能存在一个潜在问题, 即引入与目标口令完全不相关的口令.这种情况可能会对模型的训练造成干扰, 甚至可能导致通过多口令训练的模型效果不如仅使用单个旧口令训练的模型, 即综合多个信息反而导致猜测成功率下降.截至目前, 尚未有关于如何利用用户多个旧口令来提高猜测攻击成功率的系统研究.然而, 大规模的数据泄露事件使得攻击者很容易获取同一用户的多个旧口令(如含有邮箱的混合数据集中利用邮箱进行匹配), 因此, 设计利用用户多个旧口令的新型猜测方法/模型具有重要的现实意义.
6.3 基于隐式个人信息的口令猜测研究
当前关于定向口令猜测的研究尚处于初步阶段, 主要集中在如何利用显式个人信息(即能直接作为口令的组成部分) 的层面.主流的定向猜测算法(如文献[28]) 均是启发式构造用户个人信息的各种变体, 将不同类型的个人信息匹配成标签的形式, 然后再进行相应的训练和猜测生成.然而这种方式存在固有缺陷,例如, 很难穷举出用户个人信息的所有变体.此外, 这种标签匹配的方法, 无法有效利用用户的隐式个人信息.例如, 对于000Webhost 的用户, 他们大多是网站管理员, 其安全意识显著高于普通用户群体.如何利用“网站管理员” 这一隐式身份信息(群体信息) 是一个值得研究的问题.事实上, 已有研究(如文献[28])表明隐式个人信息(如教育背景、性别等) 确实会影响用户创建口令的行为.但如何量化和有效地建模这种影响, 并将其引入口令猜测算法, 仍需进一步探索.
6.4 基于大模型的口令猜测研究
随着深度学习技术的不断发展, 大型语言模型如GPT-4[95]等在自然语言处理任务中展现出了强大的能力.这些模型具备了对文本数据的高度理解和生成能力, 因此可以用于更智能化的口令猜测攻击和防御.具体而言, 大型模型能够生成更加真实且符合用户行为习惯的猜测.它们可以分析用户的语言模式、兴趣爱好, 并利用个人信息构建个体的社交网络关系(例如, 可以识别亲子关系的亲密度高于普通朋友的关系), 同时还能生成群体画像(例如, 了解儿童用户的典型特征[96]).通过对这些通用性大模型在口令数据上进行微调, 有望更有效地利用用户画像(包括各种隐式个人信息) 和社交网络关系, 从而提高口令猜测的成功率.因此, 将大模型与口令猜测研究相结合, 将为口令安全研究带来新的可能性.
6.5 口令猜测算法组合研究
2021 年, Wang 等人[73]和Parish 等人[97]的研究都表明, 组合不同类型口令模型所生成的猜测集的破解率通常高于单一猜测集.然而, 这种简单的(平均/随机) 混合方式只能得到某个固定猜测数下的破解成功率, 无法充分发挥不同模型的优势; 此外, 不同口令模型对应不同的概率空间, 对混合后字典的重新排序也是一个挑战.当前, 随着深度学习技术的发展, 不断有新的猜测方法被陆续提出, 如何有效地利用各种算法来提高口令猜测的效率成为一个迫切需要深入研究的问题.2021 年, Murray 等人[98]为解决该问题提供了新的思路: 基于多臂老虎机模型来建模口令猜测问题.具体而言, 他们将每个猜测集视为一个老虎机, 通过每次猜测来学习更多有关目标口令分布的信息.借助这些信息, 他们能够选择使用与目标口令分布最匹配的猜测集进行猜测, 从而最大化猜测收益.2022 年, Han 等人[99]分析了现有猜测方法的不同特点, 提出了一个参数化混合猜测框架.该框架由模型剪枝和最优猜测数分配策略构成, 能够利用不同方法的优势来生成更高效的猜测集.期待更多的关于组合口令猜测算法的研究.
6.6 口令策略研究
为了促使用户创建更安全的口令, 网站往往会设置复杂的口令策略, 如长度必须不少于8 位, 且必须包含两种以上字符类型.这些要求看似提高了用户使用弱口令的门槛, 但用户在生成口令时遵循省力原则, 通常会对已有口令或流行口令做出简单修改, 来对规则进行适配.复杂的口令策略既增加了用户的负担, 又未必显著提高口令的安全性.如Rao 等人的研究表明[100], 仅仅增加口令长度, 不能显著提升口令的安全性; Wang 等人的研究表明[101], 增加口令字符组成的种类, 不能提升口令的安全性.事实上, 一些看似专门精心设计的口令策略往往存在不合理之处.例如, 知名密码与信息安全期刊ACM TOPS 的投稿网站在用户注册时要求口令长度大于等于8 且至少包括两个数字[102], 那么即使口令非常强健, 像iycFsgfsgado2.Ouhspr 这样的口令, 仍然无法通过验证.其本质原因是, 网站无法准确衡量用户口令的安全性, 进而无法给出科学合理的口令生成建议.因此, 基于口令猜测算法和口令强度评测算法的研究进展, 对现有口令安全策略的系统性研究十分必要.
总之, 口令猜测研究是一个充满潜力的领域, 涉及多个学科的交叉知识, 包括密码学、统计学、自然语言处理和机器学习等, 十分具有挑战性.这一研究领域不仅具有理论深度, 还具有广泛的实际应用价值.随着计算技术的不断发展和大规模口令数据的不断泄露, 口令猜测攻击和防御之间的竞争将继续演化, 为研究者提供了丰富的机遇和挑战.相信口令猜测研究将吸引更多学者的关注和深入研究, 为建设可持续的口令安全生态提供重要的理论指导和方法支撑.

