考虑惯量增益与电网强度的VSC 稳定性分析

徐 意，李先允，程 爽，陈兰杭

（1.南京工程学院 电力工程学院，南京 211167；2.国网镇江供电公司，镇江 212002）

大规模新能源接入使电力系统向“低惯量”方向发展，传统“源随荷动”的实时平衡将受到极巨大挑战[1]。弱电网效应及其引发的电力电子装置并网稳定性问题备受关注。一方面，采用常规控制的变流器系统并网使电网缺少转动惯量，系统频率稳定问题日益突出；另一方面，以风光为代表的新能源通过长距离传输线并网，使电网呈现弱电网特征。电网频率跌落时，虚拟惯量控制VSC 系统可通过锁相环采集电网频率并利用直流链路能量快速响应频率变化，提供惯量支撑功率。但其与电网交互过程中控制参数及电网参数对系统稳定性的影响仍然需要开展进一步研究。

目前国内外学者对虚拟惯量控制的VSC 稳定性进行了一定研究，文献[2]提出利用直流链路电容能量来提供惯量的方法，并将其应用于HVDC；文献[3]提出应用于光伏系统的虚拟惯量控制，分析了系统中控制参数对虚拟惯量的影响；文献[4-6]提出基于滤波器和自适应控制的虚拟惯量控制改进策略，对提升VSC 系统惯量支撑能力有一定价值；文献[7]通过仿真分析得出虚拟惯量控制在获取系统频率过程中易造成电力系统失稳的结论；文献[8]提出虚拟同步机实现新能源发电系统无锁相环预同步控制，但控制结构复杂，对换流器的性能要求较高；文献[9]通过储能与风电机组协调控制提供惯量支撑，但储能装置增加了成本，且储能与电网的交互过程中易产生新的稳定性问题；文献[10-12]从锁相环、短路比及直流链路等角度对VSC 并网的稳定性进行分析，从机侧、网侧及直流链路出发，提出了一些致稳控制策略。

针对上述研究现状，本文考虑虚拟惯量增益及VSC 系统的详细结构，构建了虚拟惯量控制系统状态空间模型，对虚拟惯量控制增益k 变化以及电网强弱变化时系统的稳定性进行分析，较为完整的分析了该系统的适用场景及稳定范围，分析结果对其实际应用与改进有一定的价值。

1 虚拟惯量控制系统小信号建模

1.1 虚拟惯量控制系统结构

采用虚拟惯量控制的VSC 并网系统结构框图如图1 所示，分布式新能源经由虚拟惯量控制VSC 并网。ui为逆变器出口电压，if为流经LC 滤波器的电流，up为并网点电压，i 为流经线路的电流，ug为电网电压，ic为流经滤波电容的电流，Udc为直流链路电容电压。

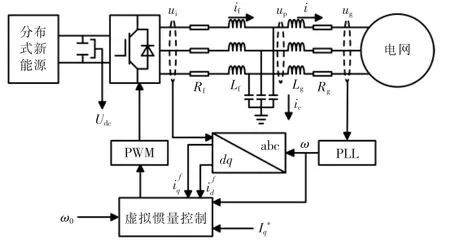
图1 虚拟惯量控制系统的结构框图Fig.1 Structural block diagram of virtual inertia control system

VSC 系统惯性时间常数H 可表示为

式中：C 为直流链路电容容量；f0为系统稳定运行时的交流频率；Udc0为系统稳定运行时的直流链路电容电压；SVSC为逆变器容量；Δ f 为发生扰动时系统的频率偏差量；ΔUdc为发生扰动时直流链路电容的电压偏差量；Udc0为直流链路电压稳态值。

滤波环节及线路阻抗对应的状态方程为

式中：iid、iiq、upd、upq分别为ii和up在d 轴和q 轴上的分量；kppll和kipll分别为PLL 环节的比例和积分系数；xθ为中间变量；Lf、Cf、Rf、Lg及Rg分别是LC 滤波电路及电网的阻抗参数。

1.2 锁相环及直流链路的状态方程

图2 锁相环的原理图Fig.2 Schematic diagram of phase locked loop

将并网点电压的q 轴分量调为0，引入状态变量θ，可得锁相环环节的状态方程：

忽略变流器损耗，根据功率流动关系，直流链路电容状态方程为

式中：PRES为新能源发出的有功功率。

1.3 电压电流环的状态方程

电压电流环的控制框图如图3 所示，基于经典的PI 控制电压电流环并引入并网点电压前馈量，根据输入电流指令获得电压指令。

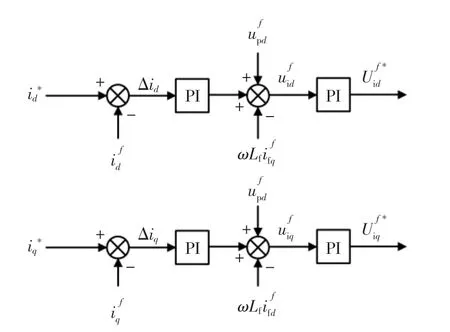
图3 电压电流环控制框图Fig.3 Voltage and current loop control block diagram

状态方程如式（11）～式（14）所示：

式中：xId和xIq为中间变量。

1.4 虚拟惯量控制环节的状态方程

虚拟惯量控制环节如图4 所示，建立Δω 与ΔUdc之间的关系，使电容电压响应系统频率变化，为系统提供惯量支撑。ΔUdc和Udc0为给定值，与Udc作差，经PI 控制器输出id*。k 越大则ΔUdc越大，由式（1）可知，VSC 可输出更大惯量支撑功率。

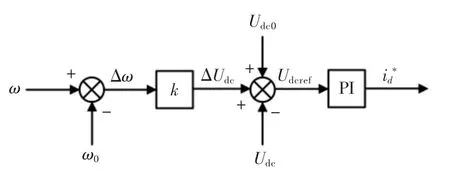
图4 虚拟惯量控制框图Fig.4 Virtual inertia control block diagram

虚拟惯量控制的数学模型如式（15）所示，其中xO为中间变量，如式（16）所示：

2 小信号模型分析

联立各状态方程，可得14 个状态变量和2 个输入变量组成的非线性微分方程组，其状态向量x 和输入向量u 分别如下所示：

在平衡点处线性化，可得系统小信号模型：

式中：Δx 和Δu 分别为状态向量和输入向量相对平衡点的偏移量；矩阵A、B 分别为系统矩阵和输入矩阵。

2.1 特征值分析

初始状态下的系统参数如表1 所示。由表1 参数得A 的特征值及阻尼比，如表2 所示。

表1 初始状态下系统参数Tab.1 System parameters in initial operating state

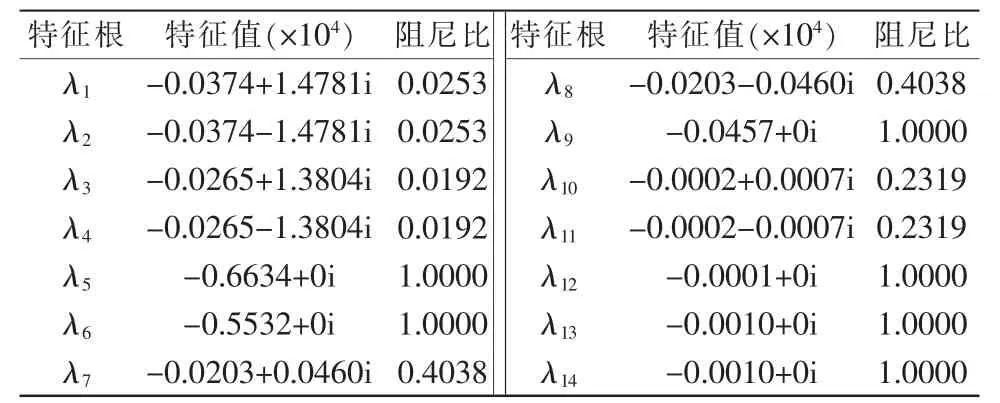
表2 小干扰稳定线性化状态矩阵A 的特征值及阻尼比Tab.2 Eigenvalues and damping ratio of small interference stable linearized state matrix A

由特征值判据可知初始状态下系统处于稳定状态，特征根均位于复平面的左半平面，有6 个振荡及8 个衰减模态。部分特征值实部接近0，系统存在不稳定风险。为获取系统稳定运行的条件，本文采用特征根轨迹对其进行分析。

电网强度常用短路比ξSCR表征：

式中：Ub、Sb分别为VSC 输出额定电压和额定功率；Zg为线路阻抗。一般情况下ξSCR越大则电网越强，那么Lg越大则电网越弱。

据表1 参数，逐步改变k 或Lg，得系统特征根轨迹如图5 和图6 所示。

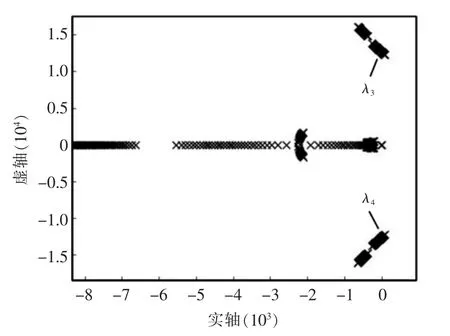
图5 k 变化时系统特征根轨迹Fig.5 System characteristic root locus when k changes

图6 Lg 变化时系统特征根轨迹Fig.6 System characteristic root locus when Lg changes

2.2 参与因子分析

为明确系统相互作用的动态环节，本文引入参与因子分析。

状态矩阵A 特征根λi对应左右特征向量Ψi，φi满足：

pki=Ψkiφki，pki为参与因子，表示第k 个状态变量在第i 个模式中的参与度。

参与因子本质上是特征值λi对系统矩阵A 主对角元素akk的灵敏度，其大小反映了状态变量对模态的影响程度，呈正相关关系。

初始状态下系统参数如表1，设置场景1 和2：

场景1：逐步增大k 至4000，其余参数不变。

场景2：逐步增大Lg至0.0005H，其余参数不变。

场景1 下：对系统初始状态下（稳定）到k=3302.6（临界稳定）再到k=4000（不稳定）过程中主导状态变量的参与因子进行计算。

场景2 下：对系统初始状态下（稳定）到Lg=0.000438H（临界稳定）再到Lg=0.0005H（不稳定）过程中主导状态变量的参与因子进行计算。

k 变化时，对于模态λ3和λ4，分析主导状态变量Δuid、Δupd、Δid的参与因子，其他状态变量的参与因子忽略不计，变化情况如表3 所示。

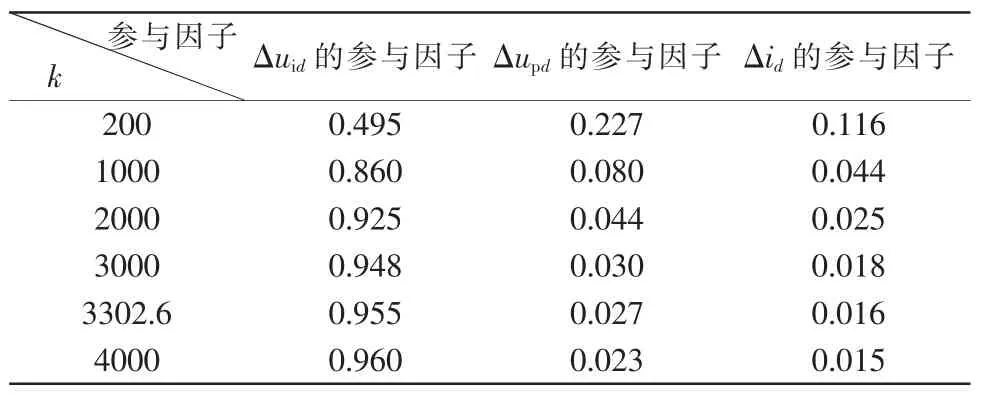
表3 k 变化过程中主导状态变量的参与因子Tab.3 Participation factors of dominant state variables when k changes

在Lg变化时，对于模态λ3、λ4，对主导状态变量Δuid、Δupd、Δid的参与因子在Lg取不同值时变化情况进行分析，其他状态变量的参与因子忽略不计，其变化情况如表4 所示。

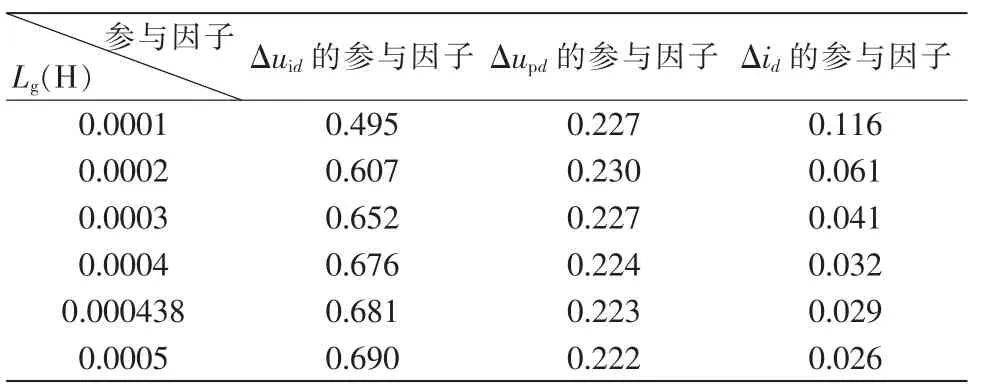
表4 Lg 变化过程中主导状态变量的参与因子Tab.4 Participation factors of dominant state variables when Lg changes

经分析，Δuid的参与因子呈上升趋势，且幅度较大，其他状态变量的参与因子均保持不变或呈下降趋势。结合系统结构分析，控制环节中建立的基于并网点前馈电压的dq 轴耦合关系，是使虚拟惯量控制VSC 在弱电网场景下失稳的主因。

分析结果说明，电网强弱变化时合理选择惯量增益参数，可确保系统稳定，并获取最大的惯量增益。

3 仿真分析

根据图1 所示系统结构在Matlab/Simulink 软件搭建仿真模型，结合稳定性分析结果，对系统在k和Lg分别变化时进行仿真分析。

系统稳定时的并网电压波形应为三相正弦波；当k 或Lg变化时，可得系统临界稳定时和失稳时的并网电压波形，如图7 所示。系统临界稳定时系统输出电压波形不再是标准的正弦波形，而是电压幅值反复波动的波形；失稳时其波动幅度更大，且变化周期不固定。

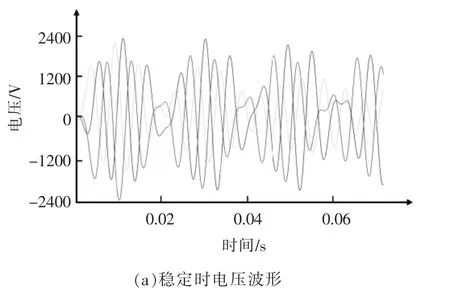
图7 系统临界稳定及失稳时并网点电压波形Fig.7 Grid-connection point voltage waveform when the system is critically stable and unstable

仿真结果与稳定性分析所得的稳定条件相对应，说明了对特征根轨迹及参与因子分析的正确性，所建立的状态空间模型可正确表征系统在惯量增益系数k 和电网强度变化时的稳定性特征。

4 结语

本文对虚拟惯量控制的VSC 并网系统的状态空间模型及稳定性进行研究，建立了其详细模型，通过特征根轨迹和参与因子对系统在虚拟惯量增益变化及电网强弱变化时的失稳原因进行分析，通过Matlab/Simulink 软件的时域仿真结果验证了所建立模型与分析结果的正确性。

采用虚拟惯量控制的VSC 并网系统的稳定性受虚拟惯量增益大小及电网强弱影响，且二者影响系统稳定性的主导特征根相同。在弱电网环境下虚拟惯量控制VSC 系统的稳定性难以得到保障，或虚拟惯量增益较小，因此该系统更适用于强电网，此时其惯量支撑能力强，稳定性好。在实际应用中，需考虑电网强弱的动态变化过程，对虚拟惯量控制系数进行折衷选取或动态优化。本文所得结论也有助于在未来对系统进行补偿器设计与改进。