基于联邦滤波的仿生偏振组合导航系统滤波器设计

葛文强，高 航，王 悦，张 昱

（北京无线电计量测试研究所，北京 100854）

仿生偏振光导航技术是近二十几年来兴起的一种导航误差不随时间积累、自主性强的导航技术。非洲沙蚁（Desert Ants）能够感知天空偏振光的分布模式，判断出其身体长轴相对于太阳子午线的夹角，然后根据当前时刻推算其地理系偏航角[1]。研究人员们模仿沙蚁对偏振光的感知过程，研制了仿沙蚁的偏振光传感器用来测量航向角信息。仿生偏振组合导航方法类似于地磁矢量组合方法，它提供载体系三轴太阳矢量信息并与SINS 系统提供的载体系太阳矢量信息作差，以提供三维量测信息，达到姿态测量的作用。和现常用的导航定位系统相比，仿生偏振光导航具有无源、无辐射、隐蔽性好等特点，是导航研究的重大研究方向。

常用的MIMU/GPS/磁强计组合导航方法获取自身姿态、速度及位置信息，然而野外未知环境下，GPS 系统易发生信号失锁、信号遮挡与干扰问题，地磁传感器易受矿藏、建筑和其他钢铁结构引起的磁场异常与罗差等干扰。仿生偏振导航技术具有无源无辐射、隐蔽性好、不受外界干扰、误差不随时间累积等特点，本文引入仿生偏振导航系统与捷联惯性、GPS 导航系统进行组合，设计无重置型组合导航联邦滤波器。此类组合模式的设计，在检测出GPS失锁或受电磁干扰时，通过隔离SINS/GPS 子系统，进行仿生偏振/MIMU 系统重构，能够在离原始区域一定范围内，保持导航系统的姿态精度与系统稳定性。

本文针对野外导航系统在动态未知、多源干扰环境下难以工作的问题，设计具备环境适应能力的仿生偏振/MIMU/GPS 组合导航系统。系统引入仿生偏振导航技术，以捷联惯导为公共参考系统建立各子滤波器与主滤波器模型，提出针对系统几种组合模式的智能切换方案，判断并隔离受干扰的GPS 子滤波器，以提高仿生偏振组合导航系统的环境适应性，以成功应用于野外地面运行环境。

1 传感器模型建立

1.1 仿生偏振传感器输出建模

针对基于偏振分光棱镜的仿生偏振导航传感器[2]，载体系下偏振传感器的输出为单位太阳矢量由载体系中三轴太阳矢量Sb、量测噪声vs构成，vs为零均值高斯白噪声。表示为

1.2 陀螺输出建模

陀螺输出信号yg，t包含了真实角速率ωt，零偏εg，t以及高斯白噪声vg，t，如式（2）所示：

经过四元数解算过程，陀螺零偏εg，t是引起三维失准角的主要误差源，陀螺零偏bg，t属于低频、慢变过程，有ε˙g，t=0；vg，t为零均值高斯白噪声。

1.3 加速度计输出建模

加速度计输出信号ya，t包括重力加速度gt，载体运动加速度at，加计偏置Δa，t以及高斯白噪声va，t，如式（3）所示：

本文利用加速度计信号校正惯导姿态，此时运动加速度、加计偏置（at+Δa，t）为干扰因素。通常加计偏置选择模型Δ˙a，t=0。而在载体运动加速度建模方面，文献[3]进行了广泛的研究。考虑运动加速度下一时刻的取值概率，载体受外力使其运动加速度产生变化，受载体（视为刚体）自身固有频率的约束，下一瞬时的运动加速度取值必定在当前值的邻域内[3]。根据文献[3]，运动加速度表述为

式中：at、at-1分别为当前时刻与上一时刻的运动加速度；参数ca（0≤ca≤1）的取值确定了运动加速度的截止频率；wa，t为白噪声。将式（4）进行进一步推导，得到如下的运动加速度微分方程：

2 仿生偏振组合导航系统联邦滤波器设计

构成组合导航系统的子系统有：捷联惯导系统（SINS）、GPS 导航定位系统（GPS）、仿生偏振导航系统（PZ）。选择惯导为公共参考系统，与其余子系统分别组合，构成2 个子滤波器，则联邦滤波器结构如图1 所示。其中，为增强子滤波器2 的可观测度，在量测模型中加入了加速度传感信息，构成MIMU/仿生偏振组合模式。子滤波器给出SINS 及相应子系统状态的局部最优估计，主滤波器按照融合算法合成关于惯导状态的全局最优估计。为了GPS 受严重干扰时，滤波器的强容错性可使干扰系统得以有效隔离与快速恢复，采用无重置型联邦滤波结构，分配系数在各子滤波器中合理分配，本文中选取β1=0.5，β2=0.5。

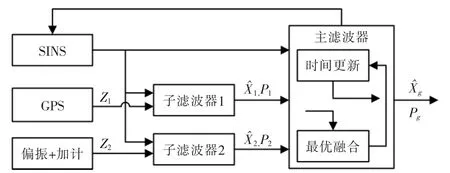
图1 仿生偏振组合导航系统滤波器Fig.1 Bionic polarized-light integrated navigation system filter

2.1 SINS/GPS 子滤波器建立

选择惯导系统状态：

式中：φE，φN，φU为数学平台失准角；δVE，δVN，δVU分别为载体速度误差；δL，δλ，δh 分别为经纬度和高度误差；εx，εy，εz，分别为陀螺随机常值漂移和加速度计随机常值零偏。状态向量共15 维。状态方程为捷联惯导误差方程：

式中：以陀螺加计噪声为系统噪声。

系统的噪声转移矩阵GINS为

系统的状态转移矩阵FINS为

式中：FN的非零元素表示见文献[4]。Fs表示为

惯导与GPS 形成的量测方程为

式中：V1＝[nxnynznvxnvynvz]T为量测噪声，位置、速度量测方程表示如下：

2.2 MIMU/仿生偏振子滤波器建立

选择惯导系统三维失准角、三维陀螺常值漂移状态量，以及三维加速度计干扰量，作为子滤波器状态量

状态方程表示如下：

系统状态转移矩阵为

Fa=diag［caxcaycaz］，系统噪声矢量w3为陀螺仪随机噪声：

系统的噪声转移矩阵G3为

MIMU/仿生偏振形成的量测方程：采用加速度计、偏振传感的量测输出，与MEMS 惯导推导所得载体系下重力加速度矢量、太阳矢量之差，作为量测量建立六维量测方程。

（1）SINS/加速度计量测模型：由捷联惯导计算得姿态转换矩阵，其对应的载体系重力加速度矢量：

（2）SINS/仿生偏振量测模型：由捷联惯导计算得三轴太阳矢量表示为

式中：Sn为根据天文年历，在已知经纬高、时间参数而求解得到的地理系下太阳矢量。载体系下偏振传感器的输出为由载体系中三轴太阳矢量Sb、量测噪声vs构成，表示为

根据式（16）～式（19），对式（20）进行推导：

因此，MIMU/仿生偏振的量测方程建立如下：

为加计与仿生偏振传感器的量测噪声。

2.3 最优合成算法

如图1 所示的联邦滤波器结构（βm=0，无重置）的主滤波器信息分配系数为0，主滤波器不参与滤波。此时，主滤波器状态量与全局估计取值相等：

3 系统智能切换性设计

野外运行于未知、动态及多源干扰环境，野外环境中树木、建筑以及GPS 人为干扰会严重影响GPS信号的正确性，另外，MIMU 也会因长时间工作而疲劳失效。野外地面导航系统对动态未知环境的适应性、抵抗外界多源干扰问题，成为了提高其组合导航系统可靠性的关键。系统组合模式的智能切换方案设计如图2 所示。

图2 仿生偏振/MIMU/GPS 系统组合模式的智能切换方案Fig.2 Intelligent switching scheme for combination mode of bionic polarized-light/MIMU/GPS system

由图2 可以看出，当GPS 导航失效时，SINS/GPS子系统被隔离，导致系统速度与位置参量无法更新。但在该情况发生位置一定区域范围内、一定时间段内，天空太阳矢量的变化很小，较真实太阳矢量为极小值，可以忽略。因此，在无GPS 情况下，组合系统仍能保持较好的精度。

在系统针对组合模式的智能切换方案中，对于MIMU 的容错性设计，采用余度传感的结构来提高MIMU 的可靠性，通过直接比较法、广义似然比法[5]来检测MIMU 子系统的可用性。在SINS/GPS、MIMU子滤波器中均采用χ2检验法[5]确定GPS 量测信息的有效性，以确定子滤波器的可用性。以上算法可检测并判定子滤波器的可用性，一旦确定子滤波器不可用，便阻断其输入主滤波器。主滤波器使用其余未受干扰的子滤波器进行如式（23）、式（24）的最优融合，得到地面组合导航系统三维失准角状态的全局估计值。

4 仿真验证

为验证仿生偏振/MIMU/GPS 组合导航滤波器的可行性，通过仿真验证不同组合模式的基本性能。利用轨迹发生器生成路线，进而利用偏振光瑞利散射模型，生成叠加干扰的偏振传感器数据，进行仿真实验。仿真分别进行了基于联邦滤波的仿生偏振/MIMU/GPS（以下简称三组合）、仿生偏振/MIMU（以下简称二组合）两种组合方式的估计性能比较与分析，验证各组合模式滤波器的输出情况，并与常规SINS/GPS 组合模式的估计性能进行比较，如图3 和图4 所示。

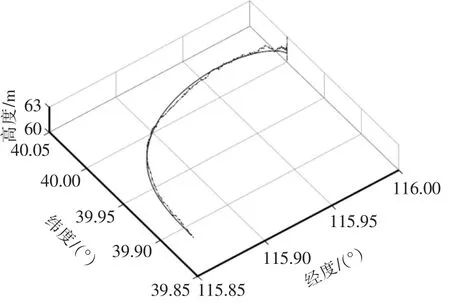
图3 运动轨迹Fig.3 Path of particle

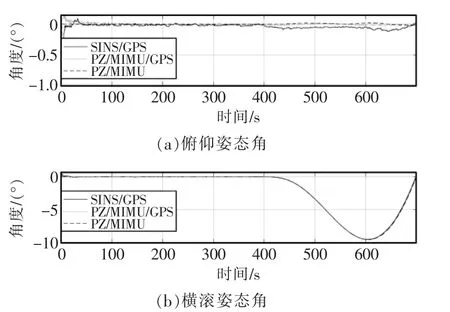
图4 各组合模式姿态角输出对比Fig.4 Comparison diagram of attitude angle output for various combination modes

（1）仿真条件：陀螺零点漂移25°/h，加计常值偏 置800 ug，GPS位置误差2.5 m，GPS速度误差0.1 m/s；陀螺仪随机噪声20°/h，加计随机噪声600 ug，磁强计随机噪声15 nT，偏振随机噪声0.01（单位：1）。

（2）仿真结果：运动轨迹为400 s 静止、300 s 盘旋半周，初始失准角为-0.9°、0.6°、0.7°。

根据上一节对于系统组合模式的智能决策方案可知，当检测出GPS 系统受干扰不可使用时，系统重构成为仿生偏振/MIMU 组合模式。从仿真结果中可看出，除SINS/GPS 模式外，三组合、二组合模式均能够保证对惯导三维失准角的有效估计。在400 s 静态情况下（如图5 所示），SINS/GPS 组合方式无法保证航向姿态角可观测性，并且对三维姿态角的估计误差较大；而其他三组合、二组合模式均能保持较高的精度并保证航向角的可观测性。在动态情况下（如图5 所示），三组合模式对三维姿态角估计精度最高，其次为仿生偏振/MIMU，SINS/GPS模式估计精度最低。从各组合模式失准角估计过程中（如图6 所示）依旧可看出，仿生偏振/MIMU/GPS三组合模式对失准角估计性能最优，仿生偏振/MIMU组合模式次之，而SINS/GPS 组合模式无法保证航向失准角较好地估计，其估计性能最差。

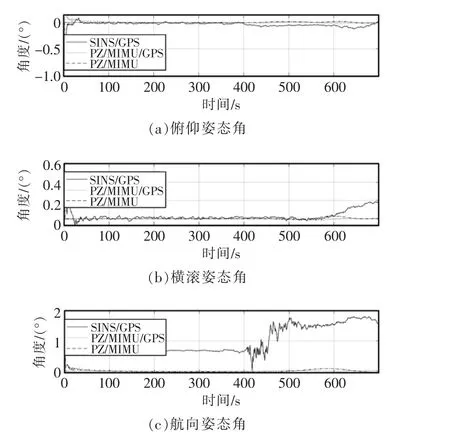
图5 各组合模式姿态误差对比Fig.5 Comparison chart of attitude errors in various combination modes

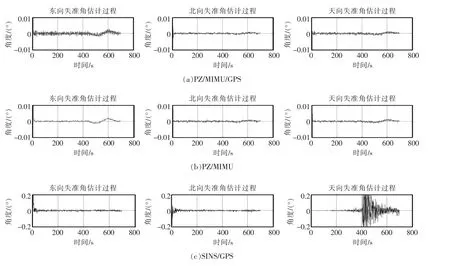
图6 各组合模式失准角估计过程Fig.6 Process of estimating the misalignment angle of each combination mode

通过仿真实验，验证了组合导航系统进行干扰子滤波器隔离、系统重构等智能决策的措施后，仿生偏振/MIMU 组合模式的基本性能。与SINS/GPS 组合模式相比较，仿生偏振/MIMU/GPS、仿生偏振/MIMU组合模式能够保证系统准确的估计性能，并且系统姿态精度、失准角估计性能、可观测性均优于SINS/GPS 模式。

5 结语

本文针对导航系统在动态未知环境下GPS 受干扰而无法正常使用的问题，设计具有环境适应能力的仿生偏振组合导航联邦滤波器。首先引入仿生偏振导航技术，组成无重置型联邦滤波结构的仿生偏振/MIMU/GPS 组合导航系统，建立各子系统的干扰模型。其次，为提高系统对于动态未知环境的适用性与抗干扰性，利用联邦滤波器优越的容错能力，设计系统针对几种组合模式的智能切换方案，有效检测并隔离GPS 干扰子系统，实现可用系统的重构。

最后通过仿真实验，验证了组合导航系统进行干扰子滤波器隔离、系统重构等智能决策的措施后，仿生偏振/MIMU 组合模式的基本性能。结果表明，仿生偏振/MIMU 组合模式能够保证系统准确的估计性能，其姿态精度、失准角估计性能、可观测性均优于传统的SINS/GPS 模式。