液黏调速系统传动机理建模与仿真分析

刘 峰,张 琳,汪首坤

(1.山东港口烟台港集装箱码头有限公司,山东 烟台 264000; 2.北京理工大学 自动化学院,北京 100081)

引言

液黏传动是继液压、液力传动之后第3种以液体为工作介质的新型流体传动技术,其具有结构紧凑、重量轻、效率高、能实现无级调速等优势[1-2]。现已被广泛应用于军事、煤炭、石油等领域的风扇传动、风机、水泵等大型机械设备中,并已取得了显著效果[3-5]。

液黏离合器其原理是通过多个摩擦副间黏性液体的油膜剪切力来传递动力,其存在内部结构复杂、模型和结构参数受温度影响较大,时变的参数导致模型的参数难于精确获取等问题,因此基于其机理建模分析十分困难[6-7]。

目前国内外学者主要集中在对其摩擦副沟槽结构、传动介质热特性、油膜的承载力分布研究[8-10],如MENG Q[11]、XIE F等[12]分别从液黏调速装置的油膜厚度及摩擦片沟槽结构参数对传递扭矩的影响进行研究;WANG Q等[13-14]研究了摩擦副在不同边界约束下的温度场变化及热屈曲行为;崔建忠等[15]分析了系统参数对液黏柔性传动动态特性的影响;谢海波等[16]研究了科氏力和温度对液黏传输的综合影响;黄家海等[17]研究了液黏离合器在流体润滑及混合摩擦两个阶段的接合特性;WANG Y等[18]在考虑径向油槽结构的情况下研究了带排转矩对液黏离合器的影响。

综上可知,目前对液黏的研究均是对其摩擦副结构或系统特性进行研究,针对该系统的机理建研究鲜见。本研究针对上述问题,以AMESim软件为平台,基于机理分析所建立的数学模型,建立液黏调速系统综合模型,并通过仿真与试验数对比验证了模型的可靠性。

1 液黏调速系统结构原理

液黏调速系统如图1所示,主要包括发动机、传动箱、比例减压阀、液黏离合器和负载。其工作原理是:发动机通过传动箱驱动液黏离合器的主摩擦片转动,同时比例减压阀驱动油缸运动,改变液黏离合器主从摩擦片之间的油膜厚度,而厚度不同的油膜可以传递大小不同的转矩,进而为负载提供动力。

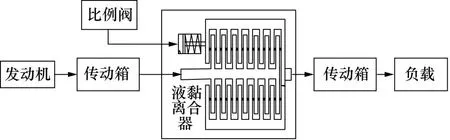
图1 液黏调速系统工作原理图

液黏离合器作为液黏调速系统核心元件,其结构如图2所示,其主要包括主动轴1、摩擦片组2、比例减压阀3、活塞4、控制油缸5和被动轴6,其中主动摩擦片和从动摩擦片是主要工作元件,通过花键分别与主、从动轴联接。工作过程中,主、从动摩擦片间隙内充满工作介质形成传动油膜,外界输入转矩和转速由主动轴经花键传给主动摩擦片,再经油膜剪切传动将动力传递至从动摩擦片,最后经花键传至从动轴乃至负载。主、从动摩擦片油膜厚度由阀控缸液压系统完成,液压泵输出流体经比例减压阀3调压后进入控制油缸5,推动活塞4运动,通过调控比例减压阀输出压力即可调控活塞4输出力,从而改变作用在摩擦片组2上的作用力,实现调控主、从摩擦片之间油膜厚度的目的,最终达到调控液黏离合器输出转速和转矩的目标,通过调节比例减压阀3的输入电流即可对其输出压力进行精确控制。

图2 液黏离合器结构原理图

2 液黏调速系统数字建模机理

2.1 流体摩擦状态下的系统受力关系

液黏离合器摩擦状态与油膜厚度密切相关,油膜厚度与受力之间存在以下关系[19-20]。

如图3所示,液黏离合器采用油缸驱动活塞的机械结构实现油膜厚度调控,活塞挤压摩擦副时,其间隙内油膜的受力情况如下:

图3 液黏离合器受力简化示意图

(1) 油缸压力对活塞的作用力F1;

(2) 每对摩擦副碟簧产生的作用力Fi2;

(3) 活塞移动时密封圈产生的摩擦力F3,其方向与活塞移动方向相反;

(4) 活塞移动时外花键产生的摩擦力Fi4,其方向与活塞移动方向相反;

(5) 当活塞挤压摩擦副间隙内油膜时,油膜将对活塞产生反作用力,此力称为油膜承载力,摩擦片上存在的油槽,当其与活塞作相对运动时产生动压承载力Fi5,其值为正;

(6) 润滑油通过静止的摩擦片间隙时产生的静压承载力Fi6,其值为正。

当液黏离合器处于流体摩擦状态时,第1个摩擦片的动力学方程:

K1(δ1-δ2)

(1)

第2个摩擦片动力学方程:

K1(δ1-δ2)-F24+F15+F16-F25-F26

(2)

第i-1个摩擦片动力学方程:

Ki-2(δi-2-δi-1)-F(i-1)4+F(i-2)5+

F(i-2)6-F(i-1)5-F(i-1)6

K(i-1)(δ(i-1)-δi)

(3)

通过对以上数学模型求解后,可得每一块摩擦片位移量δ1,δ2,δ3,…,根据摩擦副间隙初始值δ01,δ02,δ03,…,从而可得每一对摩擦副的油膜厚度δsj:

(4)

每对摩擦副油膜传递扭矩可表示为:

Mj=f(μ,ω1,ω2,δsi)

(5)

式中,Mj——第j对摩擦副油膜传递的转矩(j=1,2,3,…,28)

μ——流体黏度

ω1——输入转速

ω2——输出转速

δ——油膜厚度

液黏离合器输出总扭矩可表示为:

(6)

式中,M——总输出转矩

忽略联轴器的弹性影响,则液黏离合器驱动负载动力学方程为:

(7)

式中,Mo——负载扭矩

J——系统的总转动惯量

B——系统阻尼

在稳定或匀速工况下,液黏离合器驱动风扇系统则存在以下关系:

M=Mo+ΔM

(8)

式中,ΔM——转矩损失

2.2 接触状态下的受力关系

当外界控制压力较大时,摩擦副局部区域开始接触,此时摩擦片处于混合摩擦或边界摩擦状态。由于摩擦盘表面存在油槽,故可将摩擦副传递扭矩分解为摩擦片接触部分传动扭矩和油膜剪切传动扭矩,则第i对摩擦副机械接触部分传递扭矩如下:

(9)

式中,f——摩擦副的接触摩擦系数

k——摩擦副表面无油槽面积占比

pwi——第i对摩擦副的接触压力

(10)

式中,Fi表示每对摩擦副承受的外部法向力,与比例减压阀输出压力、控制油缸面积等因素相关。

将式(10)代入式(9)可得:

(11)

第i对摩擦副中油槽部分的油膜剪切传动扭矩为:

(12)

式中,h——摩擦片油槽深度

液黏离合器第i对摩擦副在接触状态下可传递的总扭矩为:

(13)

接触工况下液黏离合器的总输出扭矩Mc为:

(14)

2.3 比例减压阀阀建模

系统中的比例减压阀为先导式三通比例减压阀,其工作原理如图4所示,当未给比例电磁铁施加控制信号时,先导球阀在油源压力ps作用下被完全打开,主阀芯上端压力p2非常小,此时比例减压阀出口与油箱相通;当给比例电磁铁施加控制信号后,先导球阀在电磁铁推力作用下使先导级阀口过流面积减小,从而使p2增加,推动主阀芯压缩复位弹簧向下运动,达到某种平衡状态。

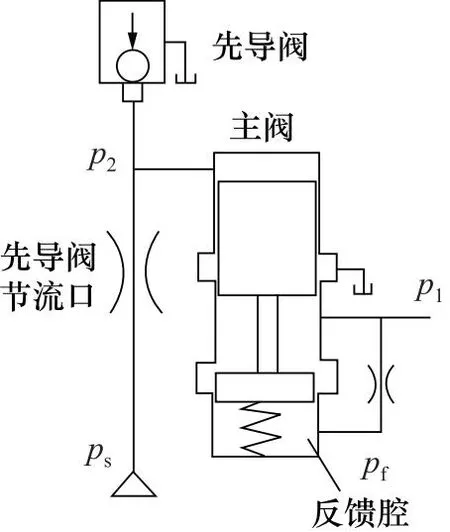
图4 比例调压原理图

稳态条件下,先导式三通比例减压阀存在以下关系:

kti=Ap2+Fs

(15)

式中,kt——比例电磁体系数

A——先导球阀作用面积

p2——主阀上腔控制压力

Fs——先导阀的稳态液动力,由于先导阀流量较小,故可忽略不计

此时式(15)可简化成:

kti=Ap2

(16)

稳态条件下,主阀芯存在以下关系:

p2Ac2=p1Ac1+Fsm+Fsp

(17)

式中,Fsm——主阀芯承受的稳定液动力

Fsp——主阀芯复位弹簧力,由于主阀芯复位弹簧刚度很小,其可忽略不计

Ac1——主阀下端面作用面积

Ac2——主阀上端面作用面积

p1——比例减压阀输出压力

忽略主阀芯稳态液动力影响,则式(17)可简化成:

p2Ac2=p1Ac1

(18)

将式(16)代入式(18),可得:

(19)

若Ac1=Ac2,则存在:

(20)

其中,式(20)是理想状态下输入电流与比例减压阀输出压力之间的关系,考虑静摩擦力等因素,该阀会存在一定死区。

3 液黏调速系统仿真与实验

液黏调速系统模型可以分为液压控制模型、离合器机械模型以及负载模型3部分,总体结构如图5所示。

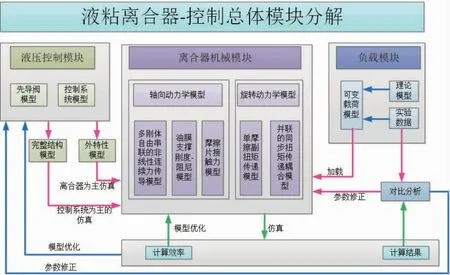
图5 物理模型总体结构示意图

3.1 液压控制模块仿真

液压控制模块如图6所示,包括先导控制外特性模型和先导控制活塞模型两部分,其系统的外部接口分别为:

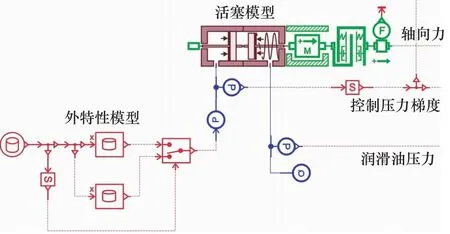
图6 液压控制模型

(1) 轴向力接口,用于传递摩擦片间的轴向力,本模块的第一个接触力为控制活塞和第一摩擦片之间的接触力;

(2) 控制压力梯度接口,用于传递控制压力的导数,传递后续计算中对离合器分、合控制方向起作用的非线性特性,分别向轴向动力和旋转动力两个方向输出;

(3) 润滑油压力接口,用于向扭矩传递计算模块和轴向力传递计算模块输出润滑油压力,考虑了控制活塞移动及活塞腔变化对该压力的影响。

3.2 离合器机械模块仿真

离合器机械模型是通过对液黏离合器工作机理分析,考虑其建模机理复杂,将每个摩擦副看作独立的单元,每个单元又包括旋转动力学模型和轴向动力学模型两部分,并简化为多自由度弹簧-质量-阻尼系统进行建模。

1) 轴向动力学模型

液黏离合器轴向动力学模型如图7所示。该模型与外部的接口主要有:

图7 液黏离合器轴向力模型

(1) 摩擦扭矩计算值输出端口,将计算得到的摩擦片传递扭矩值输入至旋转动力模块中的扭矩转递模块输出端口;

(2) 摩擦片转速输入端口,将旋转动力模块中的摩擦片转速值输入至扭矩计算函数和摩擦片接触油膜刚度阻尼模型中;

(3) 前摩擦片轴向位置输入端口,导入前方摩擦片位移,用于计算本模块油膜厚度和接触力判断;

(4) 后摩擦片轴向位置输出端口,导出后方摩擦片位移,用于计算下一个油膜厚度和接触力判断;

(5) 润滑油压力输入输出端口,用于导入润滑油压力;

(6) 非线性传递系数输入端口,导入输入压力梯度,用于计算摩擦片接触力传递和扭矩计算的非线性。

2) 旋转动力学模型

旋转动力学模块主要用于计算摩擦片之间所传递的摩擦扭矩,由轴向动力学模型中已计算得到单个摩擦片传递扭矩的数值,并提供给旋转摩擦传递模块,每个输出摩擦片受到前后两个摩擦片的共同作用。同时,每个模块的输入轴扭矩向下一个模块靠前的摩擦副传递输入转速。旋转动力学模型如图8所示。

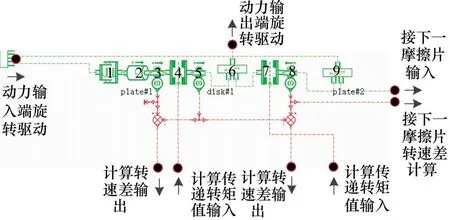
1.旋转弹簧和垫片模块 2.两轴旋转载荷模块 3、5、8.转速传感器模块 4、7.静摩擦模块 6、9.动态旋转机械节点模块

其与外部的接口主要有:

(1) 动力输入端旋转驱动输入端口,由固定转速动力源输入,用旋转驱动分离单元同步驱动14个输入驱动片,其中第一个驱动摩擦片与输入轴计算时加入一个旋转弹簧阻尼组件;

(2) 动力输出端驱动输出端口,连接整体输出端,用旋转驱动分离单元同步14个输出驱动片;

(3) 第二输入摩擦片连接端口,连接下一组摩擦副的第一摩擦副输入;

(4) 第二输入摩擦片转速差连接端口:连接下一组摩擦副的第一摩擦副转速差计算端口;

(5) 计算转速差输入输出端口,每组摩擦副连接一个,向轴向动力计算单元传递实时转速差;

(6) 计算传递转矩值输入输出端口,输入由轴向力计算单元计算得到的传递转矩值。

3.3 负载模块仿真

负载特性反映扭矩随转速的变化关系,由于液黏离合器驱动负载扭矩与转速之间存在典型二次方函数的关系。可根据流场仿真计算获得风扇转速-转矩,并建立如图9所示的负载子模型。

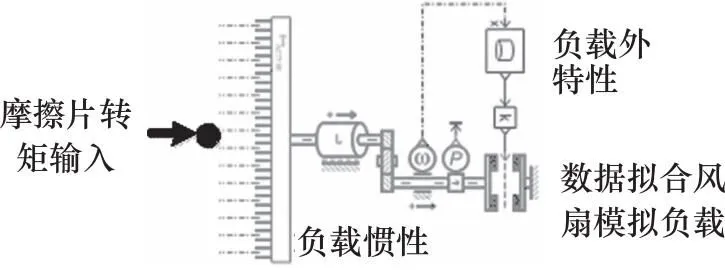
图9 负载模型

3.4 仿真与实验结果对比

为充分验证物理模型的准确性,对比不同输入转速下物理模型与实验数据的差异,故搭建了如图10所示包括电液比例阀、液黏调速离合器、液压泵、变频电机和风扇负载的实验平台,其参数如表1所示。

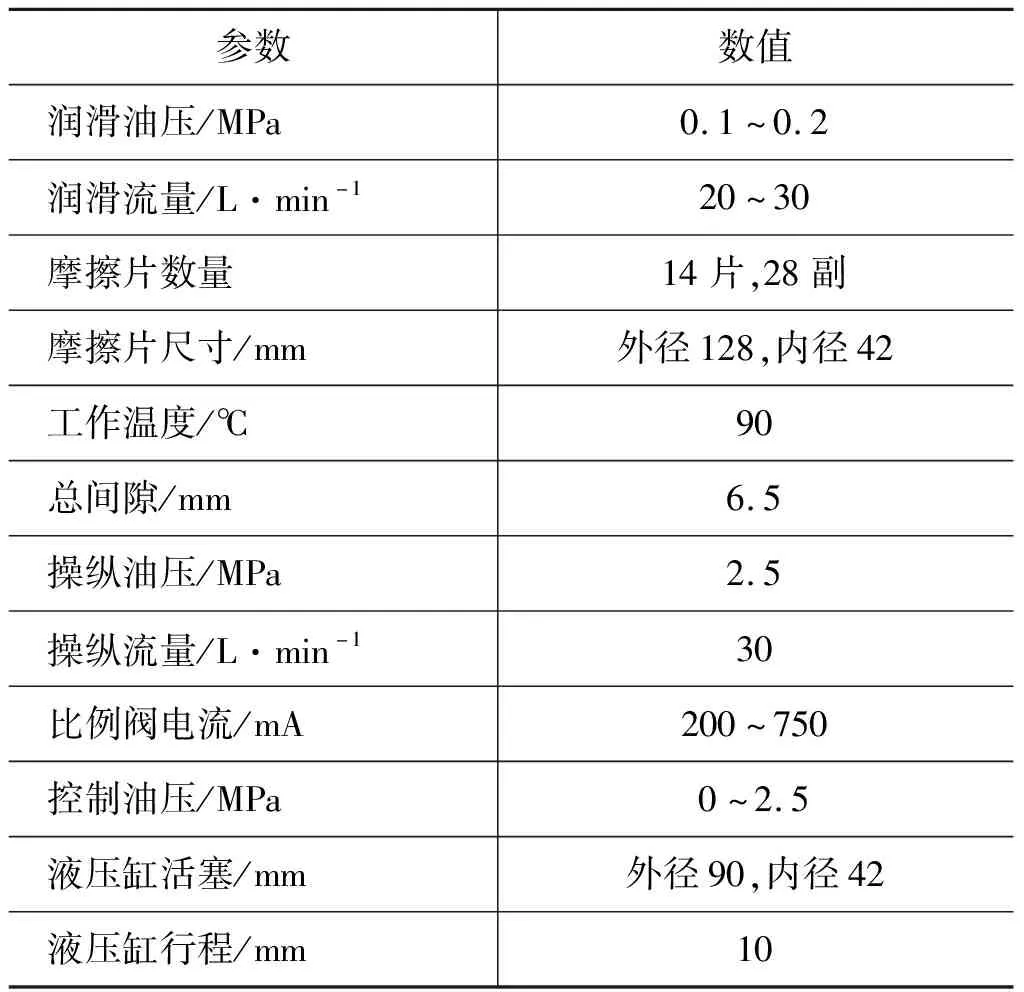
表1 实验平台相关参数

图10 实验平台

液黏输入转速(发动机转速)分别设置为4500 r/min和3500 r/min,测试模型输出和测试数据的稳态曲线差异,计算相应控制油压下的转速误差和误差百分比。

当输入转速为4500 r/min时,仿真数据与试验曲线对比曲线如图11所示,可以看出二者变化趋势基本相同,分为上升阶段和下降阶段;在上升阶段随着控制压力增大,输出转速越大,直到输入压力在0.5 MPa之后,转速达到4300 r/min左右,即到达饱和输出转速状态。

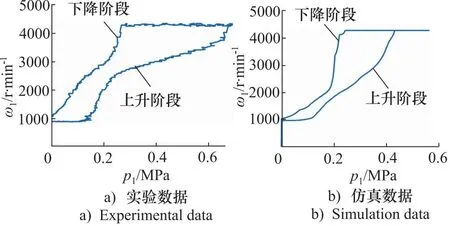
图11 输入转速4500 r/min下对比图

为对仿真模型输出结果和试验测试结果的误差进行定量描述,在两组数据中提取若干点的数值进行误差分析,输入转速4500 r/min的模型仿真数据与试验数据对比如表2所示,表中比值为误差与模型最大转速之比,可以看出,在输入压力为0.5 MPa时,仿真最大误差比值为19.81%,其主要原因是控制压力较大时实验台产生了较大振动,而液黏离合器内部结构较为紧凑,受振动影响易产生较大误差。

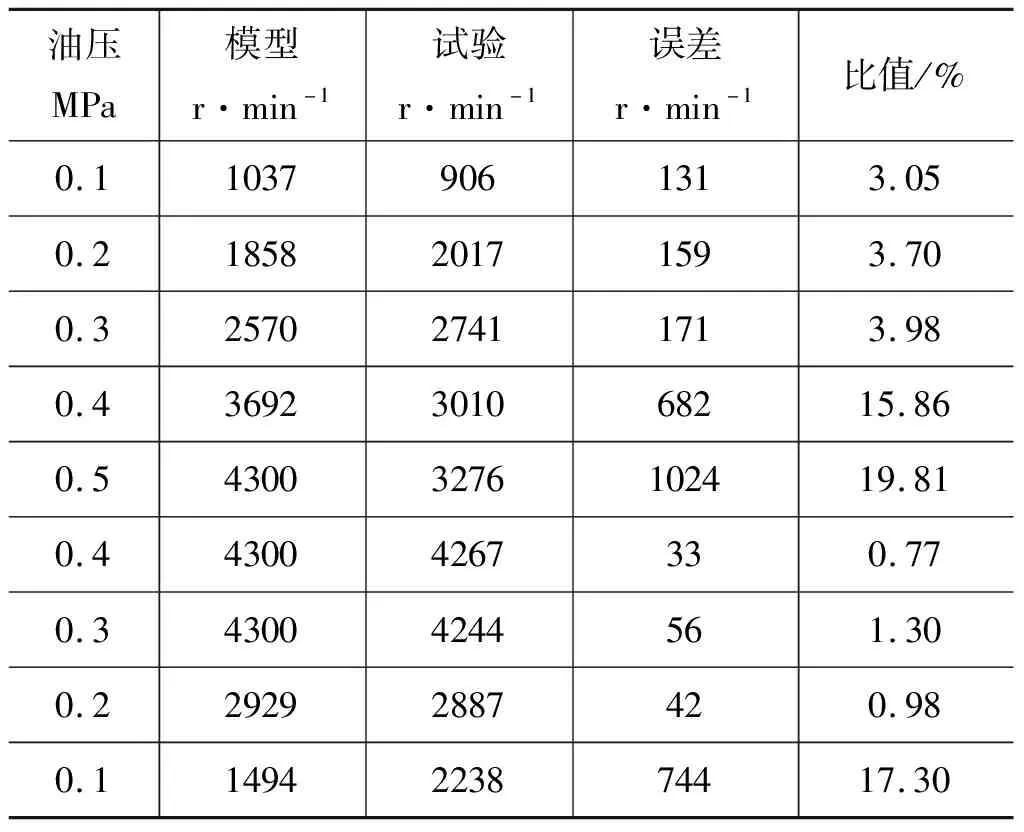
表2 输入转速4500 r/min数据对比表

当输入转速分别为3500 r/min,仿真模型输入结果与试验测试结果分别如图12所示,仿真模型输出曲线与试验曲线在外观形状上非常相似,当输入压力在0.53 MPa之后,转速达到3400 r/min左右,即达到饱和输出转速状态。

图12 输入转速3500 r/min综合模型数据与试验曲线

提取两组数据中若干点的数值进行误差分析,结果如表3所示,可以看出在输入压力为0.2 MPa时,仿真最大误差比值为19.62%。分析其主要原因在于实验初始阶段,液黏离合器由静止开始旋转存在惯性,需要较大动力,因此初始阶段易产生较大冲击,故仿真与实验存在较大误差。

表3 输入转速3500 r/min数据对比表

由上可知,液黏调速系统在控制油压增大时输出转速逐渐增大,当达到饱和输出转速状态后,输出转速不再受控制油压影响,当控制油压逐渐减少时,输出转速逐渐减少,且存在一定的迟滞。因此,液黏调速系统一体化多参数模型可以表现出实际工作中大迟滞、非线性的工作特性,在带排状态下输出转速等参数与实际效果接近,在4500 r/min和3500 r/min输入转速工况下,仿真与实验的准确度达到92.39%,为对其进一步控制提供了快速验证平台。

4 结论

针对液黏全域调速特性难以依靠单一机理模型描绘的问题,完成了液黏调速系统多参数一体化建模方法研究,建立了基于AMESim的液黏调速系统仿真模型,较准确地复现了死区、滞环、饱和和带排等特征,准确度达到92.39%,从而为控制方法提供了快速验证平台,结论如下:

(1) 在AMESim软件平台中建立了液黏离合器仿真模型,主要包括液压控制模型、轴向动力学模型、旋转动力学模型和负载模型等模块;在仿真模型中,将液黏离合器简化成28自由度质量-弹簧-阻尼串联系统,实现对任一摩擦片动力学特性的定量描述;

(2) 建立油膜刚度/阻尼与厚度、润滑油压和转速差的关联模型,描述油膜刚度/阻尼非线性特征;

(3) 液黏调速系统本质上是一个具有死区、迟滞、饱和,以及“转矩带排”的严重非线性流体传动系统,所建立仿真模型可以预测到上述典型特征,但仿真模型与试验测试结果之间还存在一定差距,其主要原因在于液黏离合器内部结构较为紧凑,受实验台振动影响生较大,且液黏离合器启动存在惯性,初始阶段易产生较大冲击,后续的研究需要进一步完善。