基于改进Hilbert-Huang变换的管路环向裂纹故障诊断研究

权凌霄,孙世博,狄梦然,李朋杰,熊国钦

(1.燕山大学 机械工程学院,河北 秦皇岛 066004; 2.燕山大学 河北省重型机械流体动力传输与控制实验室,河北 秦皇岛 066004)

引言

航空液压管路是飞机液压系统的重要组成部分,其性能优劣对飞机的安全性以及可靠性极为重要。然而,在材料制造、加工成型以及装配服役过程中,可能存在由局部薄弱点所造成的平面型缺陷,如裂纹、划痕、凹坑等。在适航载荷作用下,管路缺陷处可能会引起裂纹萌生和扩展,导致管路完全穿透性裂纹故障,最终导致管路油液泄漏,从而引发飞机安全事故。根据中国民航总局1989～2009年的统计数据,管路系统故障约占飞机元件类故障的52%[1]。其中,管路缺陷引起的航空液压管路故障是威胁航空液压管路系统安全的主要原因。

目前,国内外对结构裂纹故障诊断的方法有多种分类,总体上可分为特征提取方法和状态识别方法两大类[2]。对于一个结构系统而言,当其出现裂纹,结构整体刚度的下降导致结构自振频率也随之减小,结构的模态参数和频率响应函数随之改变。因此,对结构进行模态试验来获得结构模态参数,通过分析结构模态参数来检测和识别结构裂纹故障。其中,基于固有频率改变进行结构裂纹故障诊断的方法简单方便、误差较小。

Hilbert-Huang变换(Hilbert-Huang Transform,HHT)作为一种自适应地处理非线性、非平稳信号方法,其包括经验模态分解(Empirical Mode Decomposition,EMD)和Hilbert变换两个环节[3]。HHT首先利用EMD方法将复杂信号分解为一组本征模态函数(Intrinsic Mode Functions,IMF),并对IMF分量进行Hilbert变换,可以得到各个分量在时频面上的能量分布,进一步分析其Hilbert谱等,从中获取管路裂纹故障信号特征[4]。然而,EMD存在模态混叠问题难以获得准确的IMF。为克服模态混叠问题,由WU Z H等[5]提出了一种附加零均值和恒定标准差白噪声的集合经验模态分解(Ense-mble Empirical Mode Decomposition,EEMD)方法,其在一定程度上克服了模态混叠问题,但由于加入白噪声,计算量增加,分解过程中仍存在残余白噪声[6]。因此,在研究EMD/EEMD滤波特性及信号频率分量与噪声幅值关系的基础上提出了CEEMDAN方法,其在分解过程中根据信号的频率成分自适应地添加白噪声,消除虚假的IMF分量,有效地提高了在特征提取和故障诊断方面的性能[8-9]。李瑞等[10]采用CEEMDAN对高压隔膜泵单向阀振动信号自适应分解为IMF,通过计算IMFs的多尺度排列熵值,建立基于SO-RELM的故障诊断模型,研究结果表明,CEEMDAN多尺度排列熵能够准确表征非线性动力学特征,能够有效识别高压隔膜单向阀故障。周小龙等[11]提出一种基于CEEMDAN局部Hilbert瞬时能量谱和马氏距离相结合的故障诊断方法,其中改进的HHT方法用于提取故障特征,马氏距离用于对齿轮故障进行识别,研究结果表明,该方法可有效识别齿轮故障状态。

基于以上分析,提出一种基于CEEMDAN算法和Hilbert变换理论相结合的改进Hilbert-Huang变换方法对航空液压管路环向裂纹进行故障诊断。首先,利用CEEMDAN将非平稳的管路振动信号分解成一系列IMF;其次,基于Hilbert变换得到各IMF分量的瞬时幅值、瞬时频率以及信号的Hilbert谱对管路环向裂纹故障进行识别;最后,与传统的EMD和Hilbert变换相比。研究结果表明,改进Hilbert-Huang变换方法在管路环向裂纹故障诊断上的精准度更高,能够有效提取隐藏在管路振动信号中的不同分量,更好地保留信号中的特征信息。

1 改进Hilbert-Huang变换方法

1.1 CEEMDAN分解

CEEMDAN能根据信号的频率特征自适应地添加高斯白噪声,有效地避免了模态混叠问题,使得信号分解更加准确和稳定[12]。

首先定义Mj(·)为EMD分解产生第j个模态的算子,其次对任意信号s(t),在其中添加自适应的白噪声,即:

si(t)=s(t)+βk-1wi(t)i=1,2,…I,k=1,2,…,K

(1)

式中,wi(t)为第i次添加的白噪声;βk-1为每个阶段的噪声标准差。

(2)

对信号r1(t)+β1M1[wi(t)]进行EMD分解,则得到信号的第2个IMF分量为:

(3)

类似的,当分解层数为k时,第k-1个残余量和第k个IMF分量为:

(4)

重复上述步骤,直到所得残余量不能再提取IMF分量的单调函数或常数时为止。此时信号分解得到K个IMF分量和1个残余量,最终的残余量为:

(5)

即原始信号通过CEEMDAN方法分解为:

(6)

该方法将IMF定义为当前残差与其局部平均值之间的差值,缓解了EMD方法产生的剩余噪声问题,并解决了由于IMF数目不同而导致的最终平均问题。

1.2 Hilbert变换

对EMD分解出的IMF分量c(t),Hilbert变换y(t) 可表示为:

(7)

式中,P为柯西主值。根据Hilbert变换定义,当c(t) 和y(t)形成一个复共轭时,构造的解析函数z(t)为[14]:

z(t)=c(t)+iy(t)=a(t)eiθ(t)

(8)

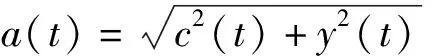
(9)

通过Hilbert变换,可以将各IMF分量转换为以时间为变量的信号瞬时幅值和瞬时频率[15]。结合式(6)～式(9),省略信号残余函数,分别对各IMF分量运用Hilbert变换并进行整合,取实部Re的原始信号可表示为:

(10)

原始信号的瞬时幅值在时间-频率平面上分布的Hilbert谱为:

(11)

2 环向裂纹管路模态试验

2.1 试验测试方案

1) 试验件制备

本研究选取两根几何尺寸相同的航空液压管路进行自由模态试验。其中,一根无裂纹缺陷,另一根存在裂纹缺陷,且裂纹形式为环向裂纹如图1所示。管路长度L为1500 mm,管路外径D为16 mm,壁厚t为0.8 mm,裂纹深度a为0.5 mm,裂纹圆周角2θ为45°,材料为不锈钢。

图1 管路环向裂纹形式

2) 试验台搭建及相关试验设备

航空液压管路模态试验台所需的硬件设备包括:试验管路、计算机、测控系统、加速度传感器、力锤及相应的连接线等,航空液压管路模态试验台搭建原理,如图2所示。

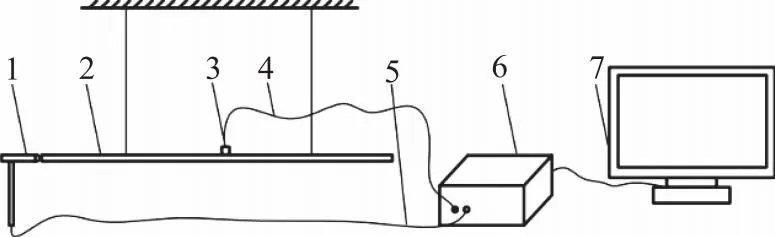
1.力锤 2.试验管路 3.加速度传感器 4.信号输出 5.信号输入 6.测控系统 7.处理器

其中,试验测控系统主要由基于NI设计平台的测控设备、基于图形化编程的LabVIEW软件和计算机显示器三部分组成,如图3所示。

图3 测控系统

3) 管路模态试验

在开展自由模态试验时,将试验管路用弹性绳悬挂于台架的型材上,并使用胶水将加速度传感器1和2从左至右安装在管路表面,如图4所示。随后,利用力锤对试验管路端部进行轴向脉冲敲击,并通过NI测控系统实现数据的采集。

图4 自由模态试验件安装

2.2 试验结果

利用MATLAB软件对采集到的振动信号进行求解,可得到振动信号时域波形和频谱,分别如图5、图6所示。由图6可知,无裂纹和有裂纹管路振动信号频谱幅值存在差异,但频率成分几乎相同,其中前4阶固有频率基本相同,分别为f1=41.02 Hz、f2=123.00 Hz、f3=243.20 Hz和f4=413.10 Hz。因此,传统的振动信号频谱无法有效诊断管路环向裂纹故障。

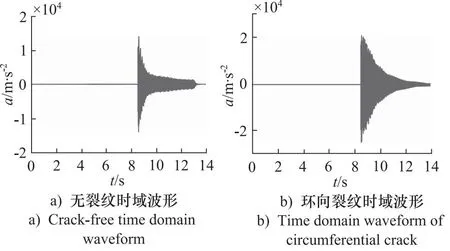
图5 航空液压管路振动信号时域波形

图6 航空液压管路振动信号频谱

3 环向裂纹管路故障诊断

本节通过对管路模态试验所采集的环向裂纹时域波形信号进行分解,论证采用CEEMDAN分解和Hilbert变换理论相结合的改进Hilbert-Huang变换相比传统EMD分解和Hilbert变换理论相结合的Hilbert-Huang变换的优越性。

3.1 管路振动信号EMD和CEEMDAN分解

采用传统EMD分解和Hilbert变换理论相结合的Hilbert-Huang变换方法分析故障振动信号。通过EMD方法对航空液压管路振动信号进行分解,从中提取出信号的细节特征。其中,环向裂纹管路振动信号共分解出17个IMF分量c1～c17和1个残余分量r18,如图7所示。

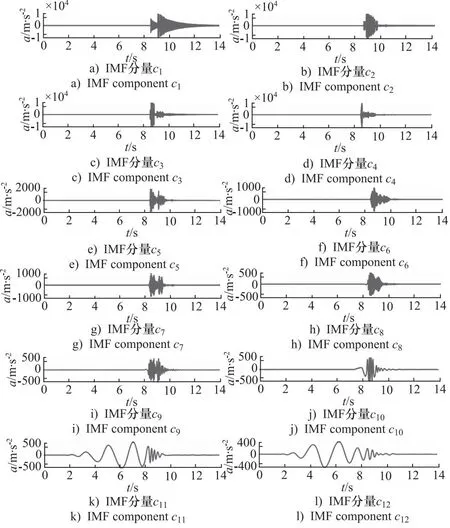
图7 EMD分解的IMF

采用CEEMDAN分解和Hilbert变换理论相结合的改进Hilbert-Huang变换分析相同的故障信号。根据信号自身特点,将CEEMDAN的参数噪声标准差β和实现次数I分别设置为0.05和100,并对航空液压管路振动信号进行分解,从中提取出信号的细节特征。其中,环向裂纹管路振动信号共分解出19个IMF分量c1～c19和1个残余分量r20,如图8所示。

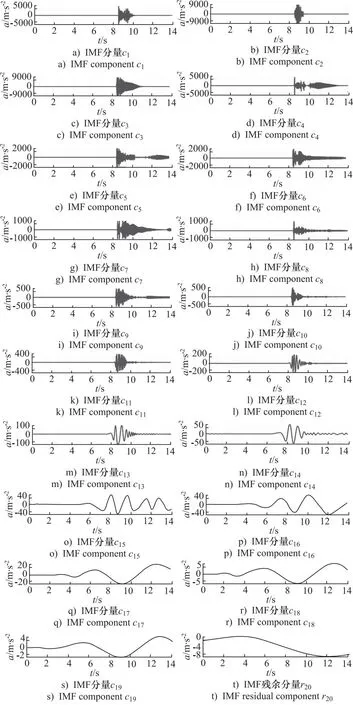
图8 CEEMDAN分解的IMF

由图7可知,EMD分解所得不同IMF分量间的模态混叠问题非常严重,部分IMF存在畸变。CEEMDAN分解的IMF如图8所示,可以看出其能有效提取隐藏在管路振动信号中的不同分量,几乎克服了模态混叠的影响。与图7中的IMF对比证实了CEEMDAN方法得到的分解结果更加准确。

3.2 IMF分量Hilbert变换分析

通过Hilbert变换,可以定义和计算信号的瞬时参数,实现真正意义上的瞬时信号提取。将分解后得到的IMF分量,通过Hilbert变换可以得到各IMF分量的瞬时幅值、瞬时频率以及信号的Hilbert谱。

1) 各IMF分量的瞬时幅值和瞬时频率

EMD和CEEMDAN分解得到的前几个IMF分量,通常集中了原信号中最显著、最重要的信息。由图7和图8可知,各IMF分量中c1～c10的信号幅值较大,因此可以忽略其余IMF分量仅选取c1～c10进行分析。

EMD分解的IMFc1～c10的瞬时幅值、瞬时频率如图9、图10所示。CEEMDAN分解的IMFc1～c10瞬时幅值、瞬时频率如图11、图12所示。可以发现,基于EMD分解Hilbert变换产生的IMF分量瞬时幅值、瞬时频率分别存在模态混叠和频率调制现象,而基于CEEMDAN分解Hilbert变换产生的IMF分量瞬时幅值按照从大到小进行排列,瞬时频率按照从高到低进行排列,因此说明CEEMDAN方法使得信号分解更加准确和稳定。

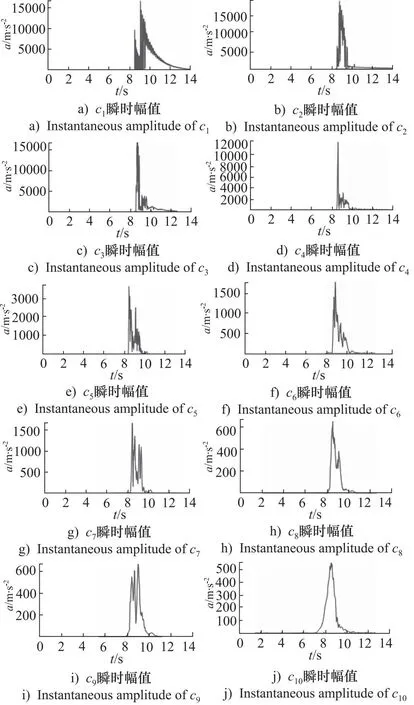
图9 EMD分解的IMF c1～c10的瞬时幅值

图10 EMD分解的IMF c1～c10的瞬时频率

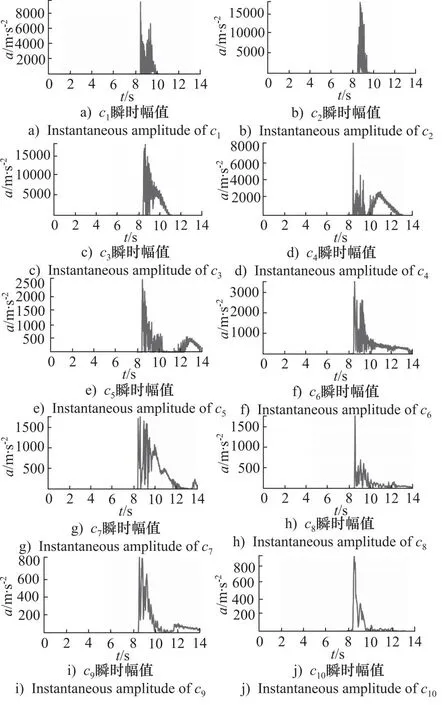
图11 CEEMDAN分解的IMF c1～c10的瞬时幅值

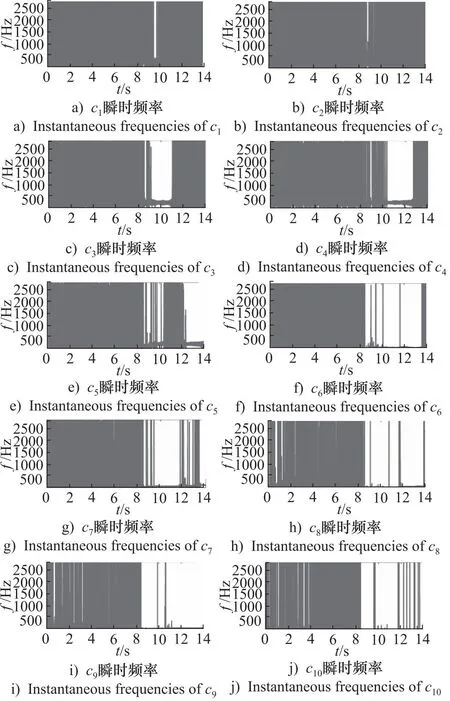
图12 CEEMDAN分解的IMF c1～c10的瞬时频率

2) Hilbert谱

Hilbert谱表示的是原始信号幅值在时间-频率平面上的具体分布情况。图13和图14分别为采用EMD和CEEMDAN方法得到的Hilbert谱。通过对比可以发现,两种方法得到的Hilbert谱均有3条明显的基频成分,瞬时频率发生波动且变化十分显著。然而,采用EMD方法得到的Hilbert谱出现了严重的模态混叠问题,采用CEEMDAN方法得到的Hilbert谱几乎不存在模态混叠问题,且各频段分量都清晰可辨。因此说明CEEMDAN方法得到的Hilbert谱更加准确。

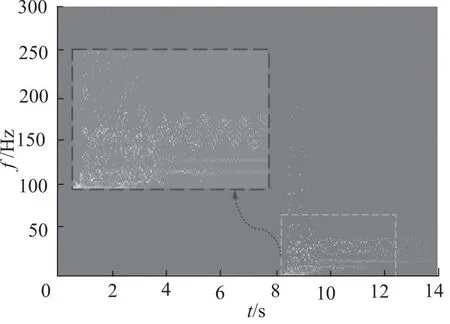
图13 采用EMD方法得到的有裂纹管路Hilbert谱

图14 采用CEEMDAN方法得到的有裂纹管路Hilbert谱

4 结论

本研究以航空液压管路为研究对象,为提高信号处理精度,提出一种基于CEEMDAN和Hilbert变换理论结合的改进Hilbert-Huang变换的信号处理方法,对模态试验中采集到的环向裂纹管路振动信号进行处理并进行故障诊断。研究结果表明:

(1) CEEMDAN分析故障信号能够克服EMD存在模态混叠的问题,获得无模态混叠的IMF;

(2) CEEMDAN相比EMD分解后各IMF分量经Hilbert变换得到的瞬时幅值、瞬时频率克服了模态混叠和频率调制现象,此外,Hilbert谱几乎不存在模态混叠问题,且各频段分量都清晰可辨;

(3) 基于CEEMDAN和Hilbert变换理论结合的改进Hilbert-Huang变换通过在信号中自适应地加入白噪声完成模态分解,对于诊断管路裂纹故障精准度更高,能够更好地识别管路裂纹故障。