TRISO颗粒SiC层辐照行为与力学性能的分子动力学模拟

严泽凡,刘泽兵,田 宇,刘荣正,刘 兵,邵友林,唐亚平,刘马林

(清华大学 核能与新能源技术研究院,北京 100084)

碳化硅(SiC)材料具有优异的力学性能、热学性能和抗辐照性能,是一类非常重要的核材料,其在先进核能系统中有广泛应用。目前SiC已被作为高温气冷堆所使用的三元结构各向同性(tri-structural isotropic, TRISO)包覆核燃料颗粒的包覆层材料[1-2],通常使用流化床-化学气相沉积(fluidized bed-chemical vapor deposition, FB-CVD)方法包覆制备[3]。在TRISO颗粒中,SiC作为主要的裂变产物阻挡层和承压层,可保证燃料颗粒的结构稳定性[4-5]。因此,SiC层对TRISO颗粒的安全性能有重要影响,有必要对SiC层的辐照行为和辐照下力学性能变化进行研究。

在辐照实验中,通常难从微观角度细致观察样品结构在辐照过程中的演化情况。采用分子动力学(molecular dynamics, MD)模拟可精确描述辐照过程中的缺陷和微观结构演变,有助于分析材料的辐照行为。目前已有大量学者对SiC材料的辐照行为进行了MD模拟研究[6-9],但目前相关研究集中在SiC单晶的单次级联或级联交叠,针对TRISO颗粒复杂的SiC层微观结构的MD级联交叠模拟有待深入研究。辐照会引起SiC层力学性能的改变,可通过纳米压痕方法获取力学性能和力学行为的信息[10],从而帮助探究SiC层因辐照发生力学性能变化的原因。MD模拟对开展纳米压痕研究有着类似的优势,有助于分析材料的力学性能。针对SiC材料的纳米压痕的MD模拟研究有很多文献报道[11-13],但研究对象大多为单一类型的SiC单晶或多晶,缺乏对辐照后的TRISO颗粒SiC层进行MD纳米压痕研究。因此,本文拟采用MD模拟详细研究TRISO颗粒SiC层在级联交叠过程中的辐照行为以及力学性能。

本文将首先通过MD模拟计算SiC在辐照中的体积肿胀理论值,以及纳米压痕下的力学性能理论值,并与实验值比较,以证明使用Tersoff/ZBL势进行SiC层的级联交叠模拟,以及使用Vashishta势和Tersoff势进行SiC层的纳米压痕MD模拟的适用性。为研究SiC层的辐照行为,考察SiC层在级联交叠过程中的辐照行为,通过肿胀程度、密度、原子结构类型、点缺陷演化等参量对辐照行为进行定量化分析,并计算不同辐照剂量下SiC层的力学性能。为进一步研究SiC层在辐照前后的力学性能变化原因,通过载荷-深度曲线、应力应变等参量对SiC层的力学行为进行定量化分析,以在微观层次解释辐照对SiC层力学性能的影响。

1 计算方法

1.1 模拟体系的提出和构建

本文研究团队对TRISO颗粒制备工艺有着长期的实验探索和优化。通过对TRISO颗粒的长期实验研究发现,不同包覆条件下制备的SiC层的微观结构不同,当包覆浓度适中、颗粒较多时制备的SiC层多为等轴状多晶,当包覆浓度极低、颗粒较少时制备的SiC层多为长轴状多晶。实验中获得的不同SiC层电子背散射衍射(electron back scatter diffraction, EBSD)图像如图1所示。

图1 TRISO颗粒SiC层的分子动力学模拟基础

采用LAMMPS软件[14]进行MD模拟,后处理主要采用OVITO软件[15]。本文使用的各类SiC层模型如图1所示。图1中的模型采用识别金刚石结构(identify diamond structure, IDS)方法[16]显示。

SiC单晶用于验证MD方法,在实际包覆中难以出现,而等轴状多晶和长轴状多晶在实际包覆中常见,故选取模型Ⅱ、Ⅲ进行辐照模拟研究。模型先在300 K、0 Pa的条件下用NPT系综进行10 ps的热平衡。然后从中随机选择1个Si原子作为初级撞出原子(primary knock-on atom, PKA),赋予其5 keV的动能,使其引发碰撞级联并造成辐照损伤。为缓解辐照引起的剧烈升温,在模型边缘设置厚度为0.3 nm、温度为300 K的恒温区,使用NVT系综控温。剩余区域为使用NVE系综的牛顿区,使其运动受牛顿第二定律控制,模拟原子间因碰撞产生的动能传递。模拟体系在x、y、z方向上均为周期性边界条件。一次辐照从赋予PKA动能开始,模拟体系在经过20 ps的碰撞级联后,在300 K、0 Pa的条件下用NPT系综对模型热平衡20 ps。级联交叠通过不断重复以上过程实现,本文共连续模拟了1 000次级联,辐照剂量达0.444 dpa。

进行力学性能研究的模拟体系包括SiC层和刚体球形金刚石压头。在压痕开始前,先将模拟体系能量最小化,然后在300 K、0 Pa的条件下用NPT系综热平衡。在压痕过程中,SiC层分固定区、恒温区和牛顿区。固定区用于固定边界原子,消除压痕过程中SiC层模型的刚体运动。恒温区在NVE系综下采用速度标定法将SiC层模型的平衡温度维持在300 K。牛顿区采用NVE系综,使其运动受牛顿第二定律控制。压头先沿z轴向下加载,并在压入SiC层表面与压头半径相同的深度后,以大小相等、方向相反的速度卸载。模拟体系在x、y轴方向上为周期性边界条件,在z轴方向上为固定边界条件。模拟过程的时间步长为0.001 ps。纳米压痕过程的模拟体系设置如图2所示。

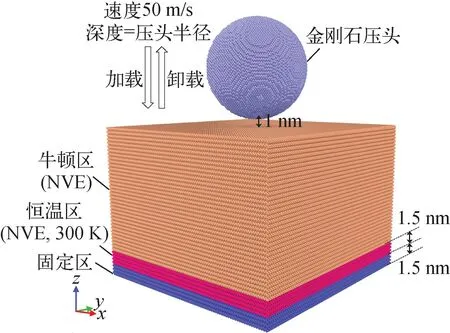
图2 纳米压痕过程的模拟体系设置

1.2 MD方法和势函数

在MD模拟研究中,势函数被用于描述原子间的相互作用,是模拟的基础和关键。本文在SiC层辐照行为研究中采用Tersoff/ZBL势描述SiC层中的原子相互作用;在SiC层力学性能研究中采用Vashishta势描述SiC层中的原子相互作用,采用Erhart和Albe[17]改良的Tersoff势描述SiC层与金刚石之间的原子相互作用以及金刚石中的原子相互作用。

Tersoff/ZBL势被广泛用于SiC辐照的MD模拟研究[18-19],其基本形式如下所示[20]:

VTersoff/ZBL(rij)=(1-fF(rij))VZBL(rij)+

fF(rij)VTersoff(rij)

(1)

其中:VTersoff/ZBL为Tersoff/ZBL势;VZBL为ZBL势,用于修正Tersoff势在描述近程相互作用时的不足;fF为一类费米函数,用于平滑地连接ZBL势和Tersoff势;rij为原子i和j之间的距离。

Tersoff势的经典形式如下所示[21]:

VTersoff(rij)=fC(rij)(fR(rij)+bijfA(rij))

(2)

其中:VTersoff为Tersoff势;fR为二体势,代表排斥作用;fA为与键合相关的吸引作用;bij为连接原子i和j的键级,代表了局部键合并确定势对键角的依赖性;fA与bij的乘积为三体势;fC为截止函数。

Vashishta势被广泛用于SiC材料纳米压痕的MD模拟研究[22-23],其基本形式如下所示[24]:

(3)

(4)

(5)

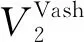
1.3 模拟方法的验证

为验证Vashishta势和Tersoff势描述SiC层力学行为的可靠性,根据Oliver&Pharr方法,计算出模型Ⅰ的杨氏模量,并与实验值进行对比,汇总列于表1。同时计算出模型Ⅰ～Ⅲ的硬度理论值,并与不同晶粒尺寸SiC多晶硬度的实验值汇总示于图3所示,此处的晶粒尺寸为多晶中晶粒的平均直径,可看出,通过MD模拟获得的力学性能理论值与实验测量值较接近。

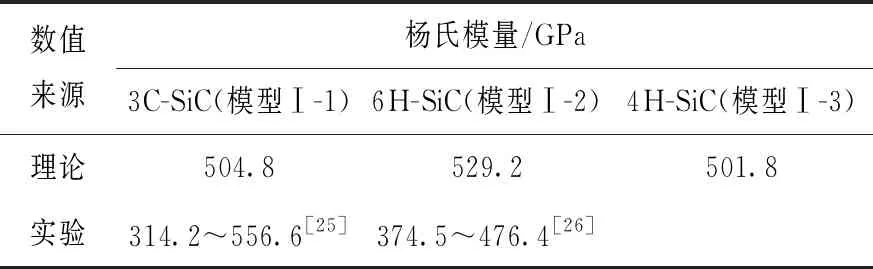
表1 SiC单晶杨氏模量的理论值和实验值对比

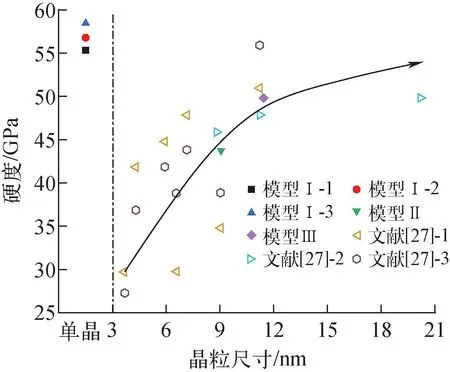
图3 模型Ⅰ～Ⅲ的硬度理论值与SiC多晶硬度实验值的对比[27]

为进一步验证Tersoff/ZBL势描述SiC层辐照过程的可靠性,对模型Ⅱ和模型Ⅲ在辐照过程中的体积肿胀程度进行计算,并与辐照得到的实验值进行对比,如图4所示,可看出,本文体积肿胀程度的MD计算结果与辐照实验结果基本一致。综上,本文采用的势能函数和相关参数可用于SiC辐照行为和力学性能模拟。

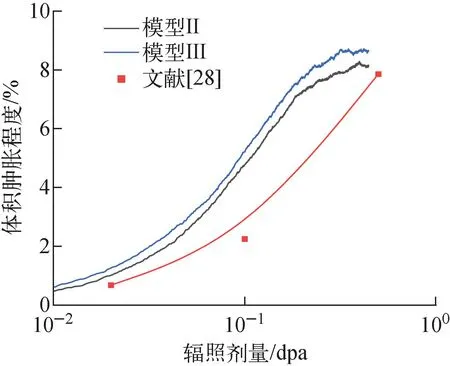
图4 模型Ⅱ、Ⅲ在辐照条件下的体积肿胀程度理论值与实验值对比[28]

2 结果与讨论

2.1 SiC辐照肿胀分析

为研究SiC层的辐照行为,给出SiC层的辐照肿胀与非晶化的演化过程,并进行定量化分析。模型Ⅱ、Ⅲ在辐照过程中的体积肿胀程度与密度如图5所示。从图5可看出,两种模型在辐照过程中发生了体积膨胀、密度下降的现象。两种晶体模型的变化过程基本一致,说明长轴晶和等轴晶受辐照影响规律类似。SiC层的体积肿胀程度先迅速升高,在辐照剂量0.2 dpa左右开始放缓,并逐渐达到稳定;密度的变化趋势与体积肿胀程度类似。

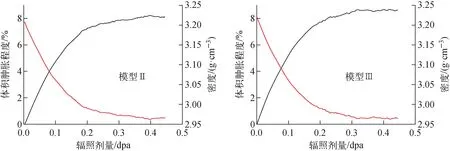
图5 模型Ⅱ、Ⅲ在辐照过程中的体积肿胀程度与密度

2.2 SiC辐照非晶化分析

通过对模型Ⅱ、Ⅲ在辐照过程中各类结构的原子比例进行统计有助于了解辐照过程中的缺陷和非晶化的演化情况,如图6所示。其中金刚石第一近邻结构和金刚石第二近邻结构可看作金刚石结构与非晶结构之间的中间态,前者更接近晶体结构,后者更接近非晶结构。两种模型在辐照过程中各类结构的原子比例基本一致。在辐照初期,晶体结构(立方金刚石)迅速减少,中间态结构(立方金刚石第一近邻、立方金刚石第二近邻)和非晶结构原子迅速增加。在辐照剂量达到0.05 dpa左右时,中间态结构原子的比例达最大,之后与晶体结构原子一起缓慢减少,共同转变为非晶结构原子。在辐照剂量达0.25 dpa左右时,晶体结构与中间态结构的原子比例基本降为0,而非晶结构的原子比例也达最大,此后一直稳定不变。值得注意的是,中间态结构中立方金刚石第二近邻结构的原子比例相较于立方金刚石第一近邻结构有一定滞后性,说明前者在一定程度上是由后者转化而来。

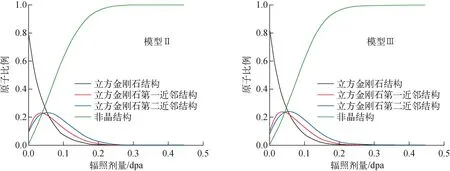
图6 模型Ⅱ、Ⅲ在辐照过程中的各类原子比例

图7展示了模型Ⅱ、Ⅲ在辐照过程中的中间态结构和非晶结构原子的演化过程,其中用红色标记了初始结构中的晶界原子,并隐去了晶体结构原子,中间态结构原子和非晶结构原子的颜色标注与图1中一致。可看出,在辐照过程中两种模型的中间态结构原子均倾向于先以团簇形式在晶界附近生成。在中间态结构原子团簇不断长大并充满晶粒内部后,非晶结构原子同样倾向于以团簇形式出现在晶界附近,并不断扩张,直至完全充满晶粒,使SiC层完全非晶化。这些现象与文献[29-30]中的辐照过程点缺陷结果基本一致。如Jin等[29]研究了晶界对SiC辐照缺陷的影响。研究表明,点缺陷倾向于在晶界附近以团簇形式积累,因为具有较高内能和拓扑无序的晶界附近的晶格比晶粒中的晶格更易受到损伤。而点缺陷的形成与非晶化过程存在强相关性,这将下文中进行讨论。这也使非晶化过程易在晶界附近发生。

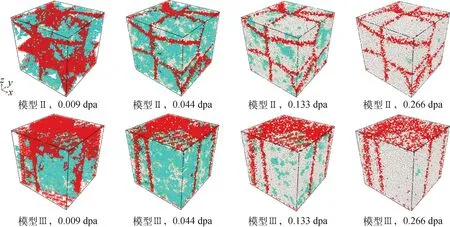
图7 模型Ⅱ、Ⅲ在辐照过程中的非晶化演化过程

以上结果说明,SiC层的辐照肿胀与非晶化存在紧密的联系,且它们不会因晶粒结构改变而发生显著改变。如对于模型Ⅱ,其辐照肿胀程度(图5)和非晶结构原子比例(图6)在辐照剂量小于0.2 dpa时迅速增加,但当辐照剂量超过0.2 dpa时增加缓慢并趋于稳定。这意味着SiC层在辐照初期辐照肿胀与非晶化程度均迅速增加,但在辐照剂量饱和后趋于稳定。辐照过程中的非晶化并非直接由晶体结构转变为非晶结构,而是存在晶体结构转化为中间态结构,再转化为非晶结构的过程,且这种过程倾向于从晶界附近开始发展。

2.3 SiC辐照Frenkel对分析

在辐照过程中会产生由空位和间隙原子构成的缺陷系统,即Frenkel对。为了解SiC层在辐照过程中的Frenkel对演化情况,可用Wigner-Seitz方法[31]统计了SiC层在辐照过程中的Frenkel对数量与各类空位和间隙原子比例。鉴于模型Ⅱ和模型Ⅲ的辐照行为没有明显差异,此处以模型Ⅱ为例进行分析,如图8所示。可发现Frenkel对数量随辐照剂量的增长与图6中的非晶结构原子类似,这说明SiC层在辐照过程中的非晶化与点缺陷的生成存在密切关系。

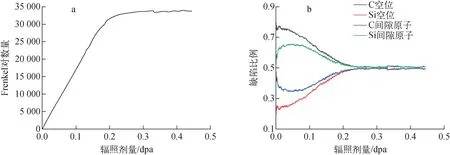
图8 模型Ⅱ在辐照过程中的Frenkel对数量与各类空位和间隙原子比例

对于空位,在辐照早期C空位的比例远大于Si空位,随着辐照剂量的增加,二者之间的比例差距逐渐减小,在辐照剂量0.25 dpa左右时,二者的比例变得几乎一样。对于间隙原子,在辐照早期Si间隙原子的比例大于C间隙原子,随着辐照剂量的增加,二者之间的比例差距先增加后减小,在辐照剂量0.25 dpa左右时,二者的比例变得几乎一样。这是因为C原子的离位阈值低于Si原子的离位阈值,所以在辐照早期C原子在辐照过程中更易离开原有点位,倾向于形成空位。而Si原子在辐照过程中位置的偏移量更小,所以更倾向于形成间隙原子。但随辐照剂量的增大,C空位和Si间隙原子趋于饱和,这些倾向表现得越来越不明显,所以C空位和Si空位、C间隙原子和Si间隙原子的比例趋于接近。

图9示出了模型Ⅱ在辐照过程中Frenkel对的演化过程,其中图9a～d为空位的演化过程,图9e～h为间隙原子的演化过程。C空位用绿色标记,Si空位用紫色标记,C间隙原子用橄榄色标记,Si间隙原子用棕色标记。可看出,空位和间隙原子的演化过程与非晶化过程类似,倾向于在辐照过程中以团簇形式在晶界附近生成,然后不断扩展并充满晶粒内部。

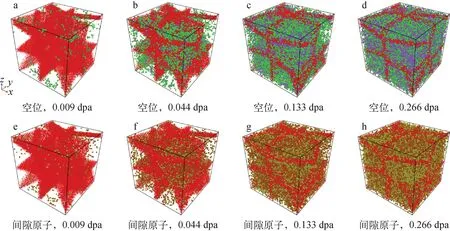
绿色为C空位,紫色为Si空位,橄榄色为C间隙原子,棕色为Si间隙原子

2.4 SiC辐照反位原子分析

在辐照过程中,也会发生某种原子替代另一种原子点位的现象,即反位原子。对于SiC,如果1个Si原子占据了原本属于C原子的点位,那么该Si原子就是Si反位原子;同理,C反位原子就是C原子占据了原本属于Si原子的点位产生的。此处同样以模型Ⅱ为例,采用Wigner-Seitz方法统计了SiC层在辐照过程中的反位原子数量与各类反位原子比例,如图10所示。可发现反位原子数量曲线与图8a中的Frenkel对数量曲线趋势基本一致。Si反位原子与C反位原子比例的变化趋势与图8b中的Si空位和C空位基本一致。这也是由于C原子的离位阈值低于Si原子造成的,所以在辐照早期C原子比Si原子更易取代对方成为反位原子。但辐照剂量的增加使Si反位原子和C反位原子的比例趋近。这种趋近现象与C原子和Si原子的离位阈值差异有关[32-33]。C反位原子更易形成,其数量在辐照过程中会更易达到饱和,这主要体现在辐照早期C反位原子的比例大于Si反位原子的比例。而Si反位原子更难形成,其数量的增加相较于C反位原子有一定滞后性,但随辐照过程的进行,Si反位原子的数量逐渐达到与C反位原子的数量接近的水平。出现图8中现象的原因也与之类似。

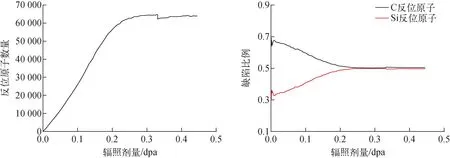
图10 模型Ⅱ在辐照过程中的反位原子数量与各类反位原子比例

图11示出了模型Ⅱ在辐照过程中的反位原子演化过程。C反位原子用橙色标记,Si反位原子用粉色标记。可看出,反位原子的演化过程与空位和间隙原子的演化过程基本一致,这说明了辐照过程中各类点缺陷的演化之间存在强相关性。

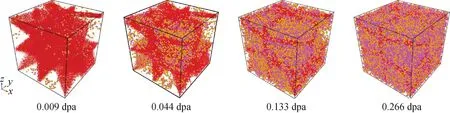
橙色为C反位原子,粉色为Si反位原子

2.5 辐照前后的力学性能分析

为了解辐照过程中SiC层的力学性能变化,对不同辐照剂量下的模型Ⅱ和模型Ⅲ进行纳米压痕测试。计算得到的SiC层在辐照过程中的力学性能变化如图12所示。由图12可知,模型Ⅱ和模型Ⅲ的硬度和杨氏模量均在辐照初期随辐照剂量的增加而迅速下降,在辐照剂量超过0.2 dpa后达到稳定,几乎不再下降。这说明模型Ⅱ和模型Ⅲ在力学性能趋势变化上是相似的。辐照会导致SiC层力学性能的降低,但在辐照缺陷趋于饱和后不再对SiC层的力学性能有显著影响。

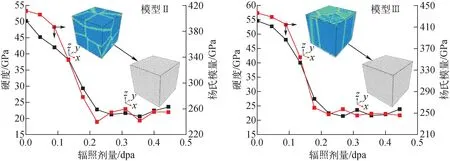
图12 模型Ⅱ、Ⅲ在辐照过程中的力学性能

为了解辐照前后SiC层在纳米压痕过程中的力学行为,汇总模型Ⅱ和模型Ⅲ在辐照前后的载荷-深度曲线,如图13所示。可看出,辐照前的SiC层在加载过程中的载荷随深度的增加迅速上升,而辐照后的SiC层则上升缓慢,使前者在加载终点时的载荷远高于后者。辐照前后的SiC层在加载过程中均发生了弹进(pop-in)现象,即加载曲线中出现了载荷的突然下降,这是弹性变形到塑性变形的转变标志。辐照前的SiC层在加载后期出现了多次明显的弹进现象,使其加载曲线较为粗糙;而辐照后的SiC层在加载过程中出现的弹进幅度均较小,使其加载曲线更光滑。这说明辐照会使SiC层在外力作用下的承受能力和塑性变形程度减小。

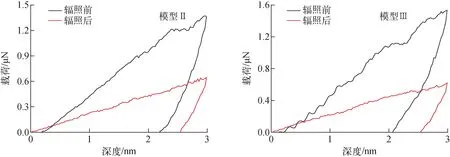
图13 模型Ⅱ、Ⅲ辐照前后的载荷-深度曲线

为了解SiC层在纳米压痕测试过程中的应力应变分布,此处计算并给出模型Ⅰ～Ⅲ和辐照后的非晶SiC层在加载终点处沿y轴半剖面的原子Von Mises应力[34]和剪切应变,同时显示了晶粒的分布,便于相互对照,如图14所示。与模型Ⅰ相比,模型Ⅱ和模型Ⅲ的应力应变分布不仅局限在压头附近,而是与晶界的分布高度相关。模型Ⅱ的应力应变分布更倾向于沿着等轴晶的晶界横向扩展;模型Ⅲ的应力应变分布倾向于沿着长轴晶的晶界纵向扩展;而非晶SiC层的应力应变分布则显得没有规律。这说明辐照会使SiC层在外力作用下的应力应变分布紊乱。

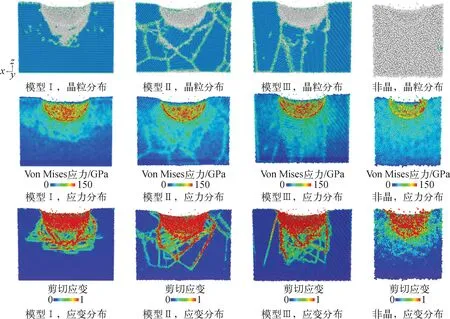
图14 模型Ⅰ～Ⅲ和非晶SiC层的晶粒分布与应力应变分布

3 结论

本文通过分子动力学模拟研究了TRISO颗粒SiC层的辐照行为和力学性能,可得出如下结论。

1) SiC层在辐照过程中肿胀程度的理论值与实验值基本一致,证明了Tersoff/ZBL势和其他模拟体系参数对SiC层辐照行为研究适用。通过Oliver&Pharr方法计算的SiC单晶的杨氏模量和各种SiC多晶的硬度理论值与实验值吻合较好,证明了Vashishta势和Tersoff势和其他模拟体系参数对SiC层力学性能研究适用。

2) 分子动力学模拟研究中,可通过肿胀程度、密度、原子结构类型、点缺陷演化等参量对辐照行为进行定量化分析。SiC层的晶粒结构对其辐照肿胀与非晶化影响较小。SiC层的辐照肿胀与非晶化程度在辐照初期迅速增加,但在辐照剂量饱和后趋于稳定。辐照过程中的非晶化并非直接由晶体结构转变为非晶结构,而是存在晶体结构转化为中间态结构,再转化为非晶结构的过程。在点缺陷的演化过程中,C原子和Si原子的离位阈值差异导致点缺陷在早期以C空位、Si间隙原子和C反位原子为主,但随着辐照剂量趋于饱和这些差异逐渐消失。非晶化和点缺陷倾向于从晶界附近开始发展。长轴晶和等轴晶受辐照影响规律类似。

3) 分子动力学模拟研究中,纳米压痕过程可通过载荷-深度曲线、应力应变等参量描述,更有助于分析辐照对SiC层力学性能的影响。长轴晶和等轴晶的受力主要受晶界方向影响。辐照会导致SiC层力学性能的降低,但在剂量趋于饱和后,不再对SiC层的力学性能有显著影响。SiC层力学性能的降低与其在外力作用下的承受能力和塑性变形程度减小、应力应变分布紊乱密切相关。