输入受限的二阶非仿射非线性不确定系统串级自耦PID控制

陈河江, 李俊丽, 王安琪

昆明理工大学 信息工程与自动化学院, 云南 昆明 650504

实际物理系统基本都是非线性系统,对非线性控制系统的研究具有较强的现实意义[1]。目前,国内外诸多学者在非线性控制领域已取得了丰硕的研究成果,诸如滑模控制[2]、反步控制[3]、自抗扰控制[4]、模糊PID控制[5]等。但这些非线性控制方法往往都只针对仿射非线性系统,面对非仿射非线性控制系统时还需进一步研究[6]。

执行器饱和现象是工程应用中普遍存在的问题[7],诸如电机的最大转速、机械装置限制的最大位置等。然而,目前控制领域对于输入受限的非仿射非线性不确定控制系统的研究仍然较少[8]。

经典PID控制因其设计简单、易于实现等优点,目前仍占据着工业市场的主导地位。但传统PID控制似乎在平稳性和快速性之间存在着不可调和的矛盾,这引起了长沙理工大学曾喆昭学者的注意。曾喆昭学者通过对控制系统的量纲进行分析,揭示了传统PID量纲冲突的问题与不协调控制的机理,进而通过阐明PID增益之间的内在关系提出了自耦PID控制理论[9]。

自耦PID在经典PID的基础上通过量纲匹配原则,科学地阐明了自耦PID控制律的理论依据,并且通过自适应速度因子将传统PID控制的三个可调参数耦合成一个参数,极大地降低了参数整定的难度,具有较大的工程应用价值[10]。

根据自耦PID的控制律不难发现,积分环节和微分环节的系数阶次都较传统PID有了大幅度的增长。因此,针对控制系统期望轨迹为单位阶跃的情况,文献[9]所采取的解决方式是给予一个过渡过程,将期望的阶跃信号过渡为一个单增的平滑信号,以此解决超调量可能过大的问题。然而,所增加的过渡过程环节无疑再为控制系统带来了额外的负担,系统的动态性能也可能因过渡过程而受限。

本文针对一类输入受限的二阶非仿射非线性不确定系统设计一种串级自耦PID控制策略,解决文献[9]中需要额外添加过渡过程的问题;并针对串级控制所带来的参数增多的问题,设计一种新的串级自耦速度因子,使广义位移环和广义速度环的可调参数耦合,进一步降低控制器的调参难度。

1 问题描述

1.1 输入受限的二阶非仿射非线性不确定系统

本文所考虑的二阶非仿射非线性不确定系统与文献[9]中的仿真实验4—实验6所考虑一致,为

(1)

其中,x1、x2是系统的两个状态量,u为控制输入量,y是系统输出量,f(x1,x2,u)是不确定的未知系统函数,d1是未知外部有界扰动。

将系统的未知不确定系统函数和未知外部有界扰动定义为总和扰动,即

d=f(x1,x2,u)+d1+b0u,

(2)

其中,b0≠0是控制增益的估计值,无需精确估计。为了避免因b0不同取值对实验结果造成干扰,本文与文献[9]保持一致,均取值b0=1。

由此,可得受控误差系统为

(3)

考虑到物理系统执行器饱和情况,设系统输入受限条件下的最大输入幅值为um=5。

1.2 自耦PID控制

自耦PID控制器(Self-coupling PID,SCPID)模型为

自耦PI控制器(Self-coupling PI,SCPI)模型为

自耦PD控制器(Self-coupling PD,SCPD)模型为

其中,定义Zc>0是控制器的速度因子,自适应律为

其中,0<α<100,β=1/Tt,Tt是过渡过程时间,文中设定Tt均取值为1 s。

在文献[9]的仿真实验中,针对期望轨迹为单位阶跃信号的情况,使用了如下的过渡过程:

r(t)=1-e-ωt。

由于过渡过程的存在,使得被控系统实际所跟踪的期望曲线并非单位阶跃信号,而是过渡曲线。如此,过渡过程的设计极有可能对控制器的性能造成一定的影响。

为了验证此猜想,分别取ω=4、5、6复现文献[9]中的仿真实验5,即SCPID的阶跃跟踪控制实验。实验结果如图1所示。可见,过渡过程的设计确实会对控制系统的阶跃响应情况造成一定的影响,这无疑为控制器的设计造成了额外的困难和不确定因素。

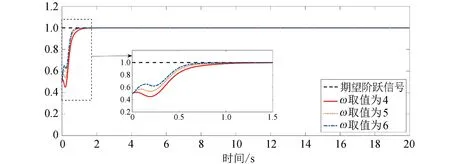
图1 过渡过程对实验结果的影响

2 控制器设计

2.1 串级自耦PID控制(SCPD-PI)

本文针对一类二阶非仿射非线性不确定系统设计了一种串级自耦PID控制器(SCPD-PI),控制系统框图如图2所示。

图2 串级自耦PID控制系统框图

为了遵循自耦PID的量纲匹配原则,串级自耦PID控制系统分为外环广义位移环和内环广义速度环。外环采用SCPD控制,内环采用SCPI控制。SCPD-PI控制律为

(4)

其中,ut为外环广义位移环控制器的输出,也是内环广义速度环的输入,Zo>0为外环的控制器速度因子;uc为内环控制器的输出,也是受控系统的输入量,设定uc的受限幅度为um=5;Zi>0为内环控制器的速度因子,e4为广义位移环的输出量与系统状态量x2的偏差量,e3为广义速度环输入误差量的积分。

2.2 串级耦合速度因子

串级自耦PID因内外环控制结构将可调参数定义为内外环的速度因子Zi、Zo。考虑到内外环的积分环节和微分环节权重较大,在动态响应初期可能会因为控制量饱和而出现超调与震荡现象,故本文延续了文献[9]中的速度因子设计策略,内外环的速度因子分别设计如下:

其中,0<α1<100,0<α2<100,Tt和β均算作既定参数,因此,实际可调参数为α1和α2。

鉴于SCPID和SCPD的一大优势是仅有一个可调参数,极大地降低了调参的难度。而串级自耦PID将可调参数扩增为两个,无疑加大了调参的难度,在一定层面上损失了自耦PID的优势。

本文设想内外环的参数之间也存在着某种耦合关系,因此对串级自耦PID的内外环参数α1和α2采用控制变量法进行调参实验。

取α1=2.5,α2=10、40、69、70,分别进行4组正弦信号跟踪对照实验,实验结果如图3所示。当广义速度环的参数α2一定时,在一定范围内,广义位移环的参数越小,则越容易出现超调甚至不能有效跟踪期望响应的情况;广义位移环的参数越大,系统动态响应效果越好,但是一旦超出某个界限,控制器的输出将会发生震荡。综上,在4组参数里面选择了表现最好的α1=2.5和α2=69作为最优速度因子组合。

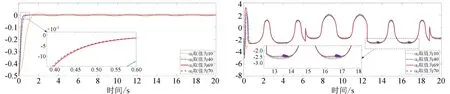
(a) 正弦信号跟踪响应误差曲线 (b) 系统虚拟控制输入量曲线

采用同样的实验方法可以得到:当广义位移环参数α1一定时,在一定范围内,广义速度环的参数α2越小,越容易出现不稳定的情况;广义速度环的参数α2越大,系统动态响应速度越快,而一旦超出某个限定范围,则会出现控制器输出震荡的情况。

为了实现串级自耦PID内外环参数的耦合,以控制变量法寻找内外环参数的最优参数组合,共记录了最优组合参数160组数据。如图4所示,通过MATLAB对最优参数组合进行数据的多项式拟合,得到如下的耦合关系:

图4 MATLAB数据拟合图像

定义α0为串级耦合速度因子,考虑到内外环参数范围受限的情况,为避免因参数过大或过小引起震荡或者崩溃的情况,不宜取值过大或过小,综合考虑取1.5<α0<7(具体取值范围可根据调参经验粗略估计即可)。

3 合理性分析与稳定性证明

3.1 广义速度内环

对于式(1)所示的一类二阶非仿射非线性不确定系统,当输出量为可测量的状态量x2时,系统中的x1可视作与反馈量x2有关的系统内部不确定函数。将系统未知不确定函数和外部扰动统一定义为总和扰动,即可将式(1)改写为

(5)

重新定义广义速度内环的受控误差系统为

(6)

由此,将一类二阶非线性非仿射不确定系统的广义速度内环可以看作一类一阶线性不确定仿射系统。

由广义速度环控制系统框图(图5)可知,反馈量y′具有广义速度量纲,输入量uc具有广义加速度量纲。针对此类广义一阶系统,文献[9]证明了采用自耦PI控制器可以实现量纲匹配原则,故在广义速度内环采用SCPI控制具有控制量量纲匹配的合理性。

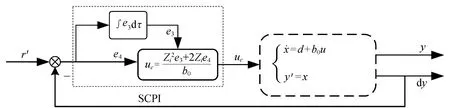
图5 广义速度环控制系统框图

定理1 假设式(5)定义的总和扰动有界,当且仅当Zi>0时,由式(4)定义的串级自耦PID控制系统的广义速度内环是全局渐近稳定的,且具有良好的抗总和扰动鲁棒性。

证明由式(4)定义的SCPI控制器代入式(6)所示的受控误差系统,可得闭环控制系统为

(7)

闭环控制系统的传递函数为

(8)

单位冲激响应为

h(t)=(Zit-1)e-Zit,t>0;

(9)

时域解为

e1(t)=-e1-h(t)+h(t)d(t)。

(10)

由式(8)可知,当Zi>0时,闭环控制系统传递函数的双重极点位于s平面左半边,因此广义速度内环是大范围稳定的。

综上可得,广义速度内环在SCPI的控制下,具有大范围稳定性和抗总和扰动鲁棒性。

3.2 广义位移外环

对于广义位移外环,可将广义速度内环的SCPI控制器与二阶不确定系统模型视作整体被控对象,内环控制器的作用作为受控模型未知总和扰动d的一部分,将系统未知不确定动态和外部扰动定义为总和扰动,可得如式(3)的受控误差系统。

因此,可将广义位移外环视作一类二阶非仿射非线性不确定系统的SCPD控制,控制框图如图6所示。

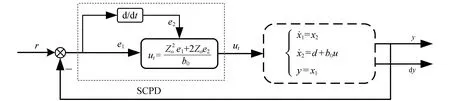
图6 广义位移环控制系统框图

由图6可知,系统反馈量y具有广义位移量纲,输入量ut具有广义加速度量纲。针对此类广义二阶系统,文献[9]证明了SCPD控制可以实现量纲匹配原则,故在广义位移外环采用SCPD控制器具有控制量量纲匹配的合理性。

定理2 假设式(2)定义的总和扰动有界,当且仅当Zo>0时,由式(4)定义的串级自耦PID控制系统的广义位移外环是全局渐近稳定的,且具有良好的抗总和扰动鲁棒性。

定理2的证明过程与定理1类似,不再赘述。

综上可得:区别于串级PID控制使用的“无量纲比例增益与相互独立增益”的概念,串级自耦PID继续遵循了自耦PID的量纲匹配原则,具有控制量量纲匹配的合理性,且具有大范围稳定性和抗总和扰动鲁棒性。

4 数值仿真实验分析

为了验证串级自耦PID控制方法的优越性,所考虑的受控系统如式(3)所述,且与文献[9]的仿真实验4—9进行了对比分析。本节所有仿真实验的串级耦合速度因子均取值为α0=2.5。

仿真实验1 SCPD-PI的单位阶跃跟踪控制

仿真实验在MATLAB/Simulink中的具体连线如图7所示,后续仿真实验与之类似,不再重复描述。实验结果如图8所示,SCPD控制达到稳态的时间为1.490 s,SCPID控制达到稳态的时间为2.008 s,SCPD-PI控制达到稳态的时间为0.585 s,系统动态响应速度明显提高;三种控制策略都表现出了较强的抗干扰鲁棒性。其中,SCPD与SCPID由于阶跃响应情况下使用了过渡过程,故误差用过渡曲线与实际值做差得到。SCPID控制的跟踪误差产生了明显的超调,而SCPD-PI则收敛较快且较为平稳。在考虑输入受限的情况下,给系统添加了阶跃外部扰动,根据控制输入量可以明显看出SCPD-PI控制器受干扰下的输出量更平缓,控制性能更好。

(a) SCPID控制Simulink仿真实验

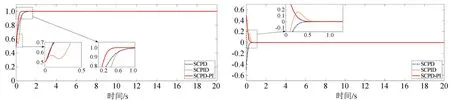
(a) 阶跃信号跟踪曲线 (b) 阶跃跟踪误差响应曲线

仿真实验2 SCPD-PI的正弦跟踪控制

仿真结果如图9所示,SCPID的跟踪误差产生了明显的超调,且在控制器输出中产生了震荡现象,控制效果最差。SCPD和SCPD-PI的动态响应速度近乎一样,但SCPD控制的跟踪精度较SCPD-PI的明显更差。SCPD-PI控制既能保证较快的响应速度也能保证较高的控制精度。

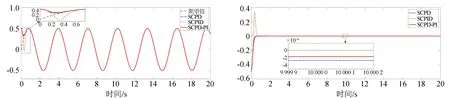
(a) 正弦信号跟踪曲线 (b) 正弦跟踪误差曲线

仿真实验3 时变系统的阶跃跟踪控制

为了验证控制器对时变被控对象的优越性,将二阶非仿射非线性不确定系统式(1)中的未知动态函数另设为时变动态函数:

其中,时变参数分别为

继续使用同一套SCPD、SCPID、SCPD-PI的参数对时变系统进行对比实验,实验结果如图10所示,表现最差的是SCPID控制器,在动态响应初期产生了较大的超调量;SCPD-PI的动态响应能力明显较SCPD和SCPID更优,控制能力更好。

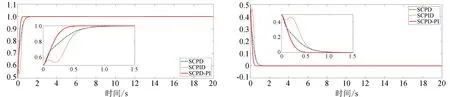
(a) 阶跃跟踪响应曲线 (b) 阶跃跟踪误差曲线

5 性能验证

四旋翼无人机是一个典型的二阶非仿射非线性不确定系统[11]。为了验证控制器的实用性,本文选取了四旋翼无人机的姿态控制模型进行控制器性能对比实验。

文献[12]验证了SCPID控制对四旋翼无人机姿态控制的有效性,但从其仿真实验中可以看出,SCPID始终具有难以消除的超调量,控制性能表现并不佳。

考虑四旋翼的姿态控制模型[13]如下式所示,具体模型推导过程可参考文献[13]:

式中,U2、U3、U4分别为滚转、俯仰、偏航3个通道的控制输入量,di为各通道的外部扰动值,I为转动惯量,绕x、y、z三轴的转动惯量分别为0.75×10-3、0.75×10-3和0.13×10-3。

分别采用SCPD、SCPID、SCPD-PI对四旋翼无人机的滚转角进行控制性能测试。取SCPD控制器的参数为α=85,取SCPID控制器的参数为α=25,取SCPD-PI的控制器参数为α0=2。给予的滚转角期望值为5,在3～6 s的时间段给予幅值为1的外部阶跃干扰。实验结果如图11所示。

(a) 四旋翼滚转角响应曲线 (b) 误差曲线

为了验证SCPID控制在有无过渡过程的情况下对系统响应性能的影响情况,分别设计了无过渡过程的SCPID响应曲线为SCPID1,有过渡过程的SCPID响应曲线为SCPID2。无过渡过程的情况下,SCPID的超调量非常大,添加了过渡过程后,超调量有所降低,但仍然无法完全消除,与文献[12]的表现一致。

对比SCPID2、SCPD、SCPD-PI三者的响应曲线可知:动态响应速度由快到慢依次为SCPD-PI、SCPID2、SCPD;无过渡过程的情况下SCPID受干扰影响所产生的超调量较大,其次是SCPD控制;综合来看,SCPD-PI不仅动态响应速度较快、无超调、无抖振,而且具有很强的抗扰动鲁棒性,可以实现四旋翼无人机姿态角系统的有效控制。

为了验证本文所设计控制策略的实用性,实物飞行测试部分采用了灵思创奇的四旋翼飞行控制实验平台,如图12(a)所示。该平台通过串口通信实现Pixhawk飞控板与相关硬件的连接,并通过WIFI通信与开发主机进行实时的数据通信,可以对四旋翼的姿态位置进行实时的监控。

(a) 飞行控制实验平台 (b) 飞行控制实验结果

开发主机及仿真环境使用Windows10(64位)平台,处理器为AMD Ryzen5-5800H。主机CPU:I7,3.2 GHz;内存:16 GB DDR4 2 666 MHz。

试验台架:四旋翼无人机起飞重量为800 g;飞控:STM32F427(180 MHz)主控及STM32F103故障安全协处理器,内置三轴陀螺仪、加速度计,5路UART,1路I2C,PPM/SBUS遥控器输入,1路ADC,12路PWM。

通过对四旋翼无人机的俯仰角进行正弦信号的跟踪实验,实验结果如图12(b)所示,在所提SCPD-PI算法的控制下,四旋翼无人机的俯仰角能够有效地跟踪期望的正弦信号,且响应速度较快,跟踪精度较高,验证了所提控制策略的有效性。

6 结论

本文针对一类输入受限的二阶非仿射非线性不确定系统,提出了一种串级自耦PID控制方法,主要工作如下:设计了串级自耦PID控制的控制结构,且延续了自耦PID的量纲匹配原则,证明了其合理性与稳定性;解决了自耦PID控制在单位阶跃响应条件下需要过渡过程的短板;设计了一个串级耦合速度因子,解决了串级自耦PID可调参数增多所带来的调参难度增大的问题;通过仿真实验对比了SCPD、SCPID、SCPD-PI的控制性能,验证了串级自耦PID的优越性;通过四旋翼无人机数学模型验证了串级自耦PID控制的有效性,为串级自耦PID的工程应用奠定了理论依据。

综上可得,所设计的串级自耦PID控制不仅具有良好的动态响应性能,而且具备较强的抗扰动鲁棒性;控制结构简单,易于设计和实现;只有一个可调参数,极大地降低了调参的难度。与文献[9]的控制方法相比,串级自耦PID在控制性能方面具有明显的优越性。