来路—思路—出路—套路,教学研题“四部曲”——基于一道高考平面向量试题的探析

⦿ 江苏省海门中学 周 茜

在数学课堂教学以及解题研究过程中,特别是在高考复习阶段,教师合理选取经典问题,多方位挖掘问题的内涵,尝试做到数学解题研究的“四部曲”——来路、思路、出路、套路,提升复习效率.

1 展示“来路”——立足课标,明确主题与指向

教材典型例、习题及历届高考真题等典型试题,具有有效巩固数学基础知识、合理渗透数学思想方法、精准明确数学学习任务、巧妙确定数学研究方向等基本作用,是新一届高考命题者改编或创编新高考题的基本“来路”.基于典型试题的教学研究,有效明确相应问题的主题,寻找典型问题的指向.

分析：此题以直线与圆的位置关系创设情境,结合从圆外一点分别引圆的切线与割线,通过“静”与“动”两种状态来设置圆上的对应点,动静结合,合理创设,进而确定相应平面向量的数量积的最值.

题目简单明了,以代数形式来叙述,以几何特征来表达,利用直线与圆的位置关系,结合圆上“动”点与“静”点之间的变化情况,勾勒了一幅优美的画卷.

2 展开“思路”——解题研究,发散思维与视角

解题研究的目的就是准确、快速地解决相应的数学问题,其实质就是合理分析与理解题目条件,综合相应的数学知识、思想方法等来合理发散思维,借助不同思维视角的切入与应用来解题,合理寻找解决问题的“思路”.这也是解题中最为关键的一个环节,不同的“思路”对应着不同的解题方法与技巧.

2.1 平面向量思维

结合问题的平面几何场景,利用平面向量思维切入,通过平面向量的数量积,以及平面向量自身“数”与“形”的双重属性来分析与求解.

方法1:平面向量法.

图1

分析：根据圆上动点的变化引入“角参数α”,结合平面向量的数量积构建三角关系式,通过三角恒等变换转化为对应的余弦型(或正弦型)函数,借助三角函数的图象与性质来确定对应的最值问题.

2.2 解析几何思维

由题意可建立平面直角坐标系,利用解析几何思维切入,通过坐标法来变形与转化相应的点、向量等相关问题,进而加以分析与求解.

方法2:坐标法.

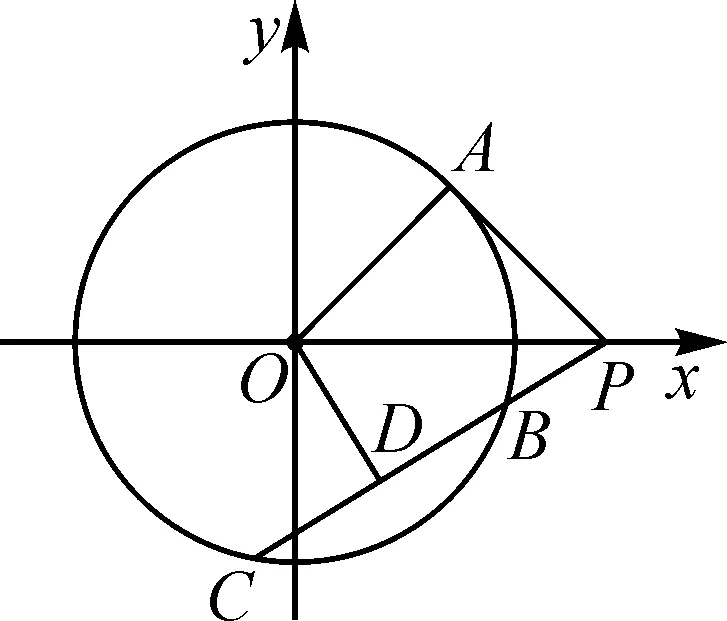
图2

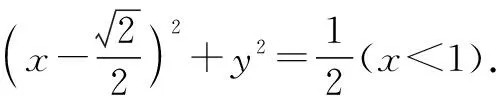
分析：根据平面几何与平面向量的问题实质,回归到平面解析几何中去,通过建立平面直角坐标系,利用点的坐标及动点的轨迹等,从代数思维视角来合理数学运算,结合动点所满足的轨迹方程进行参数方程的变换,结合平面向量的数量积以及三角恒等变换来综合与应用.构建点的坐标时,利用轨迹的结构特征,合理进行参数方程的变换是解题的关键所在.

2.3 平面几何思维

问题是平面几何,回归平面几何本质,利用平面几何思维切入,结合图形直观以及平面向量的相关几何意义加以分析与求解.

方法3：平面几何法.

图3

分析：根据平面向量数量积的几何意义,结合投影的结构特征与直观分析,通过“动”态过程中的变化规律及最值问题的几何特征,二者合理交汇与融合,通过数形结合以及图形直观,综合平面几何的结构特征与基本性质等来应用,实现问题的直观处理.平面几何法的关键就是把握图形的结构特征以及所求数量积的几何意义与内涵,合理直观与巧妙推理.

3 寻找“出路”——目标变式,链接知识与方法

目标变式是基于原问题考查的基础知识、基本思想内涵与技巧方法,有目的、有计划地合理改编与变式,探寻问题进一步的“出路”,进而凸显不同数学基础知识、基本思想方法、思路技巧等之间的逻辑关系,合理链接数学知识与思想方法,构建更加完善的数学知识体系与架构,形成更加全面的知识网络.

3.1 延续结果变式

3.2 改变条件变式

借助以上条件改变而得到的变式2及其对应的解析过程,将确定最大值的问题转变为确定取值范围的问题,还可以得到对应的变式.

4 拓展“套路”——总结反思,优化技巧与策略

总结反思是高效、合理进行解题研究的基本步骤,可以从知识覆盖面广、形式灵活的数学综合题中挖掘蕴含其中的多种解法与思想,合理总结并拓展解题的“套路”,有利于深化学生对知识的理解与掌握,从而优化数学思想与技巧策略,发展数学思维品质.

实践证明,基于数学解题研究过程中的“四部曲”——来路、思路、出路、套路,有针对性的解题研究的教学与学习,教学意图更加明显,教学思路更加清晰,教学设计与教学过程更能充分调动学生解题的积极性、主动性,是有效提高高考数学复习备考质量的一种常见教学范式.