基于循环神经网络的自适应滤波方法及应用研究

任鸿燚, 刘翔宇, 咸甘玲, 兰景岩,2

(1.桂林理工大学 土木与建筑工程学院,广西 桂林 541004;2.桂林理工大学 广西岩土力学与工程重点实验室,广西 桂林 541004)

在地震勘探中,地震波从激发、在地层中传播到地面检波器接收,最终被地震仪记录下来,过程中不可避免地混杂了一些干扰波[1-2]。干扰波与有效波在频谱、传播速度、传播方向和能量等方面存在着差异,它们并不是地下地质体的真实反映。在处理相关数据时,需要去除或压制干扰波产生的影响,从而突出有效波作用结果,提高地震资料的质量和精度。滤波作为抑制和防止干扰的一项重要举措,许多学者做了大量研究:Trifunuc[3]针对加速度时程低频成分率先提出高通滤波方法;美国地质调查局(United States Geological Survey,USGS)采用的滤波方法是以一条最佳直线拟合加速度时程零线,再从加速度时程中减去该直线[4];Boore等[5]探讨了加速度时程背景噪声的由来和特征,从加速度轨迹中减去一个或多个可以是直线或低阶多项式基线,作为一种未知频率特性的低切滤波器消除长周期噪声的滤波技术;Graizer等[6]采用最小二乘法拟合加速度时程骨架曲线消除低频成分作为滤波手段;Yang等[7]提出了最小化均方拟合加速度基线后设计窗口滤波器对加速度数据进行处理。目前的滤波处理方法基本是通过基线拟合加减和传统人为经验公式经过多次修正与结果对比,最终得到一个合适的滤波参数和加速度时域曲线。

近年来通过地震波数据反演试验,在滤波领域普遍认为USGS滤波法相较于其余方法展现出了更稳定的性能,滤波后的波形基本与原始波形保持一致,没有出现由于基线调整而产生的波峰杂乱以及被过度放大或缩小的现象。但是USGS滤波法也存在着两方面的缺陷:①滤波功能相对单一、没有针对性。不同类型的加速度时程曲线具有不同的曲线特征,在滤波处理时也应该遵循通权达变原则,对于存在高频杂音的地震波应采取部分高斯滤波部分带通滤波,而采用USGS滤波法进行滤波时只能采用统一的滤波方法,难以达到理想的滤波效果,甚至会出现信号丢失的现象。②人为经验的主观因素干预处理结果。使用USGS滤波法需要提前设置滤波参数,每一次参数的变化都会产生不一样的结果,为了得到合适的波形通常需要进行多次的尝试。为了实际操作的可行性、便利性,预先采用前期已统计的滤波参数用于同等类型地震波信号的处理。由于土体类型、震源深度的不同,所产生的干扰信号频率不同,对同类型的地震波信号将会造成有差异的影响,因而不能确保得到与前次试验相同的结果。这种单靠人为经验预先设定参数进行的滤波方法,得到的滤波结果难以保证达到最佳效果。

针对大部分滤波方法存在的弊端,借鉴目前深度学习模型在地球物理部分取得的经验,本文提出了在信号处理及系统分析领域发展迅速的神经网络系统与最小二乘法相结合,构成了一种自适应滤波法。针对时间域的信号计算RNN循环神经网络是最优选择,同时将递归最小二乘法(recursive least squares,RLS)[8]加入网络中完善了整体系统的优化性与循环结构中的鲁棒性[9]。通过大量的训练数据集对网络进行训练,使得网络内部可以从数据中自动学得输入的地震信号与期望输出的地震信号之间的误差关系,最终利用改变阶数进行缩减,对噪声的抵消和谱线增强起到了决定性作用。

1 RNN自适应滤波法的基本原理

深度学习模型具有自动获取特征规律的优势,对数据处理过程中的异常数据、掺杂数据能够自我分析及优化。针对现有的滤波方法的不足以及应用加速度时程积分速度和位移时对地震信号的精度需求,研发了一种循环神经网络[10](recurrent neural network,RNN)的自适应滤波方法,通过深度学习[11]、自我优化、参考自辨识和残差学习[12]等现代数据处理技术及MATLAB等软件丰富的函数库和自编优化算法,能够有效地避免人为因素、经验参数、频域滤波等影响。

1.1 循环神经网络应用

循环神经网络(RNN)是深度学习领域中一类特殊的内部存在自连接的神经网络,可以学习复杂的矢量到矢量的映射,如图1和图2所示。RNN由两个阶段组成:第一阶段为训练阶段,首先将含有随机噪声的测试信号Dt和不含噪声的期待信号Xt转换为矩阵形式输入编码器(Encoder)进行初步计算,再通过Kt增益向量为滤波匹配最佳滤波器阶数,即自适应,最后由解码器中神经网络单元LSTM算出最佳信号Yt,训练阶段完成;第二阶段为滤波阶段,因为经过训练后的神经网络已经能够自动识别原始信号不同频率的噪声,将原始含噪信号矩阵输入后会自动匹配滤波阶数进行计算,最后通过反归一化得到滤波后的信号。

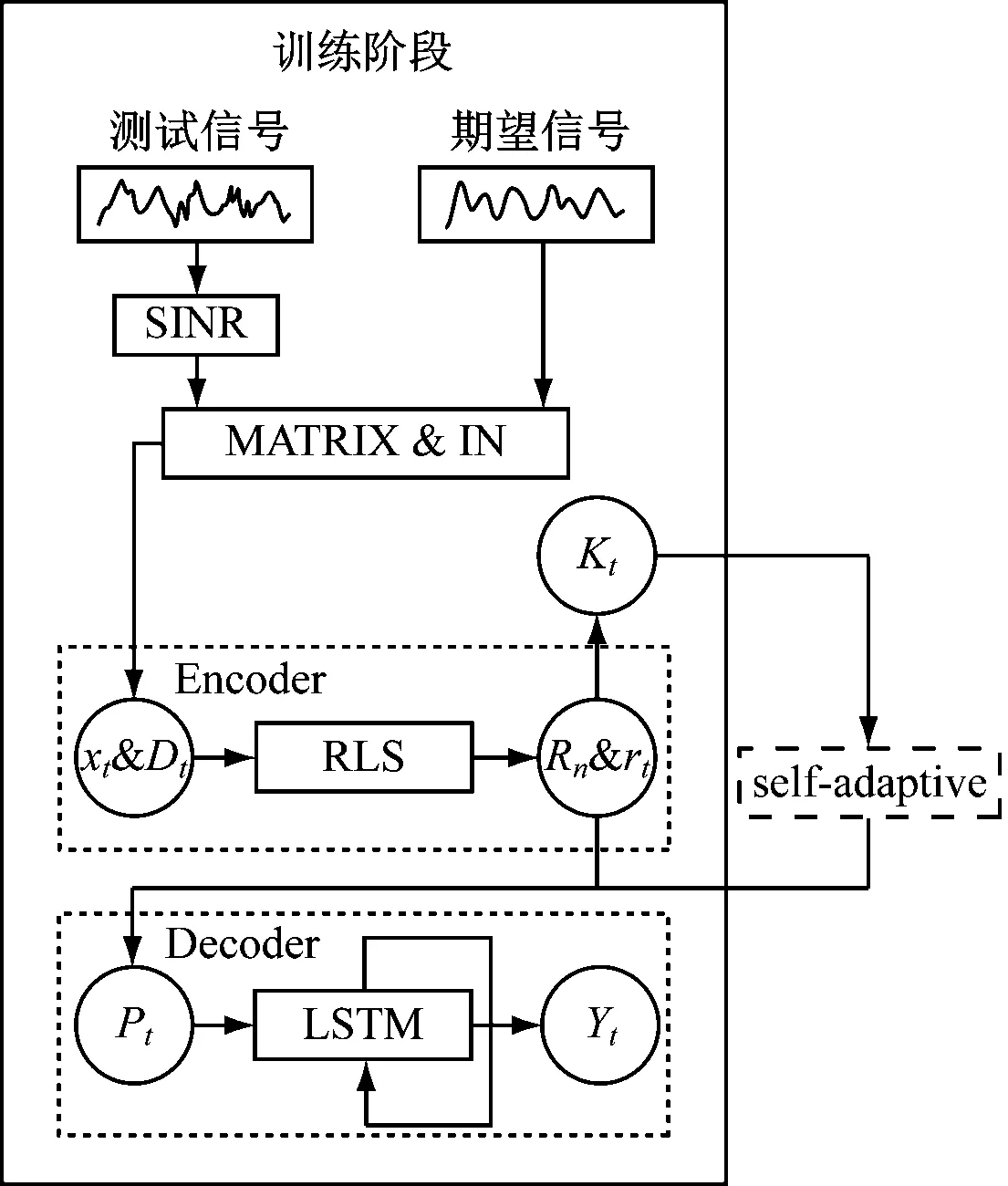
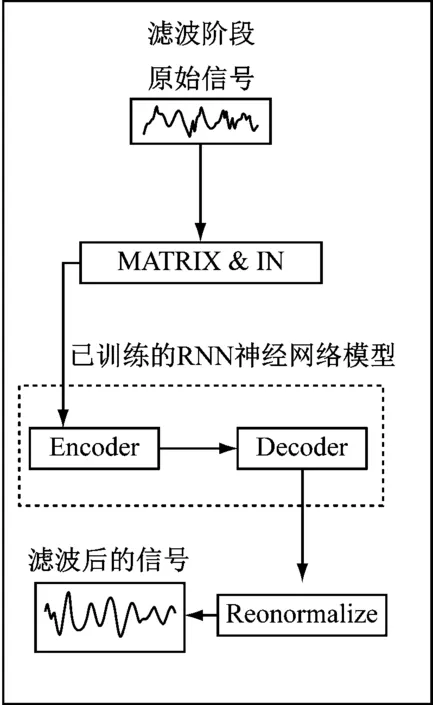
图1 RNN循环神经网络Fig.1 RNN recurrent neural network

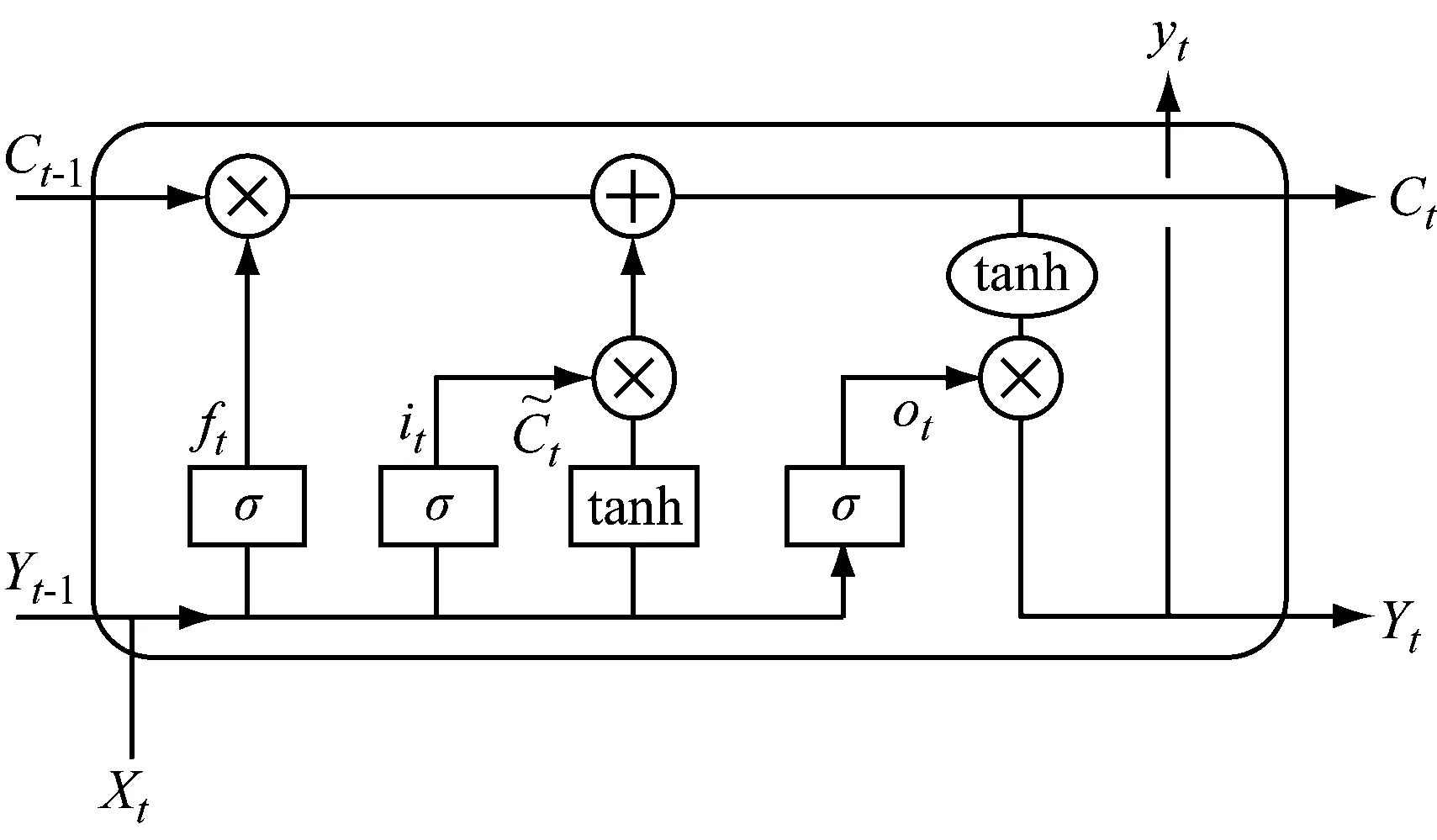
图2 LSTM神经网络单元结构示意图Fig.2 Structure diagram of LSTM neural network unit

RNN与深度神经网络[13](deep neural network,RNN),卷积神经网络[14](convolutional neural network,CNN)不同之处在于:RNN不仅考虑前一时刻的输入,而且赋予了网络对前面内容的“记忆”功能,即一个序列当前的输出与前面的输出也有关联。具体的表现形式为网络会对前面的信息进行记忆并应用于当前输出的计算中,即隐藏层之间的节点不是孤立的而是有连接的,并且隐藏层的输入不仅包括输入层的输出还包括上一时刻隐藏层的输出。加速度时程曲线在测量过程中存在较多的不可控因素,例如地层子波反射、地震波频率、背景噪声等等,这些都会对加速度时程曲线产生较大影响。常规的滤波手段需要人工调节滤波频率以及滤波阶数,通过每一次滤波后的曲线变化对滤波参数进行调整,并且时常存在过度压缩峰值、相位超前以及谱线不清晰等结果。

图2中,动态更新参数如下

it=σ(Wixt+UiYt-1+bi)

(1)

ft=σ(Wfxt+UfYt-1+bf)

(2)

ot=σ(Woxt+UoYt-1+bo)

(3)

(4)

ct=ft⊙ct-1+it⊙ct

(5)

ht=ot⊙tanh(ct)

(6)

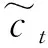
本文采用RNN自适应滤波方法滤波,通过引入遗忘调节因子赋予不同误差以不同的权重,对地震信号进行预处理,减少了LSTM神经网络数据处理的参数量,显著提高神经网络的训练速度以及数据处理的精度。遗忘因子调节方法如下:

第n次循环始终与第n-1次循环的输出结果相关,在循环中加入遗忘因子调节,对离n时刻越近的误差附以较大的权重,遗忘越少;而对离n时刻越远的误差附以较小的权重,遗忘越多。由此,对于误差的辨别分析能力相比于常规滤波手段有了更精准的控制,最终通过隐藏层内部循环以及自适应环节拟合最优滤波器阶数,达到在滤波过程中加速度时程信号与噪声信号的误差值最小的结果。

1.2 RLS算法

本文采用RLS辅助RNN神经网络进行滤波,通过RLS算法使原始含噪信号与期望信号之间的误差无限趋近于零,有效减少滤波过程中出现的峰值突刺与噪声干扰。

RLS算法是基于一种确定性思想最小化误差向量模的平方和,即:

(7)

式中:λ为遗忘因子(0<λ<1);e为误差向量;d(i)为期望加速度时程记录;x(i)为输入地震波加速度时程记录;wT(n)为第n个滤波器系数矩阵的转置。首先将Jn(w)对w求导并令梯度等于0得到关于w的公式,即

(8)

根据R(n)与r(n)的等式,可以得到其时间递推公式如下

R(n)=λR(n-1)+x(n)xT(n)

(9)

r(n)=λr(n-1)+x(n)d(n)

(10)

由于RLS算法是对输入地震信号的自相关矩阵[15]的逆矩阵Rxx(n)进行递推估计更新。推导运算k(n)每一个点的逆矩阵计算量大,求解过程复杂,因此引用矩阵求逆引理[16]是必要的。考虑到Hermitain自相关矩阵的复共轭对称性,引入时间递推公式,可得到增益向量和滤波器系数的时间递推公式,即:

(11)

w(n)=w(n-1)+k(n)ε(n)

(12)

增益向量k(n)结合遗传因子λ对加速度时程曲线特征分析与判定,建立加速度时程x(n)与最优滤波器阶数w(n-1)之间的匹配关系。式(6)中的ε(n)为先验估计误差向量,在自适应阶段对误差向量辨别分析,保证误差向量不超出最大阈值,修正w(n)权重避免滤波器阶数出现突增与骤减引起自相关矩阵Rxx(n)出现发散现象。

在循环神经网络RNN中每一次循环RLS算法都在迭代中依据上一次循环的输出误差更新参数,依据先验算误差环节对第i-1次输出误差进行分析后反馈给第i次循环的隐藏层,神经网络自动匹配最优滤波器阶数对第i次Rxx(n)滤波。此外RLS为迭代算法,通过多次迭代得到最优解,计算结果更精准。

2 RNN循环神经网络训练

网络训练[17]主要包括数据集构建、数据集归一化(或标准化)、网络训练和验证三个步骤。

2.1 数据集构建与预处理

在滤波之前基于神经网络的本身特征需要使用MATLAB软件生成训练集对RNN神经网络算法进行在线训练和优化。为了保证滤波器对真实地震波的适应性,本文选用1995年日本Kobe的地震加速度记录、1994年1月17日美国Northridge地震的302条水平向地震加速度记录和1999年9月20日台湾 Chi-Chi 地震的399条水平向地震加速度记录作为原始无噪波信号,使用MATLAB自带的噪声生成程序生成10 Hz、20 Hz和40 Hz的随机白噪声时间序列,将所有噪声各自叠加在无噪Kobe波、Chi-Chi波、Trinidad波时间序列上,合成100组含噪信号。在每组原始信号中随机截取30组长度为2 940个点的信号,共产生3 000组信号作为训练集,确保网络得到充分训练能够准确识别出不同频率下的随机白噪声以及优化自适应环节,防止过度过滤地震信号。选取与训练集Ex对应的Ey时间序列数据,将该段数据采用与合成训练集同样的方式生成20组含噪声时间序列,而后每组信号随机截取30组长度,共600组信号作为试验集,以验证网络的实际处理能力。

2.2 数据归一化

为了提高网络的收敛速度和网络精度对所选输入数据集进行数据归一化处理,并且经过归一化训练的网络会减少后期使用动力模型试验大数量级特征值加速度时程序列时对模型的计算的影响。本文采用max-min数据归一化方法根据地震波时间序列数据的特征,将其归一化至1～-1之间,计算如下所示。

对于网络的输入数据

xnorm=(xn-xmin)/(xmax-xmin)

(13)

dnorm=(dn-dmin)/(dmax-dmin)

(14)

式中:xnorm、dnorm为归一化值;xn为添加模拟噪声的地震波时间序列数据;dn为无噪声的地震波时间序列;xmin、dmin分别为有噪声与无噪声地震波时间序列数据最小值;xmax、dmax分别为有噪声和无噪声地震波时间序列数据最大值。

由于对所有输入网络的数据都进行归一化处理,网络的理想输出结果也为归一化值,输出后还要进行反归一化处理

ypred=dmax·ynorm_pred

(15)

式中:ypred为反归一化值,即网络处理后无噪声的地震波序列;ynorm_pred为网络输出的归一化预测值;dmax为网络输入的无噪地震波时间序列数据最大值。

2.3 网络训练和验证

取MaxEpochs为200(使用训练集中的全部样本训练一次即为1个epoch),Batchsize30选择小批量大小30以均匀划分训练数据,并减少小批量中的填充量,指定初始学习率为0.005,在125轮训练后通过乘以因子0.2降低学习率。

模型求解器利用自适应动量梯度下降算法计算,并调整模型各适应度参数,确保网络得到充分训练能够准确识别出不同频率下的随机白噪声以及优化自适应环节,防止过度过滤地震信号。

损失函数使用均方误差损失函数(MSEl-oos),优化器使用适应性矩估计优化器(adaptive moment estimation, Adam),该优化器具有收敛速度快、参数调整方便等优点,适合解决含有大规模数据和参数的优化问题。为了加快训练速度采用BPTT算法[18]进行训练,在训练前,需要合理初始化权重值,约束误差值的增长或缩小速度,避免出现梯度爆炸和梯度消失的问题。

图3为神经网络训练进度图,LOSS损失曲线升高代表网络训练速度减缓,峰值点代表网络训练过程中拟合遇见瓶颈,网络模型权重发生变化,训练速度达到最慢;曲线下降直到达到零值,代表训练度加快并最终完成拟合。RMSE曲线,即均方根误差曲线,曲线上升代表网络训练过程中计算出的均方根误差增大,峰值点代表均方根误差达到最大,网络将根据前一次的拟合进行修改再拟合;曲线下降代表网络训练过程中计算出的均方根误差减小,该曲线越趋近于零值证明网络拟合的效果越好。

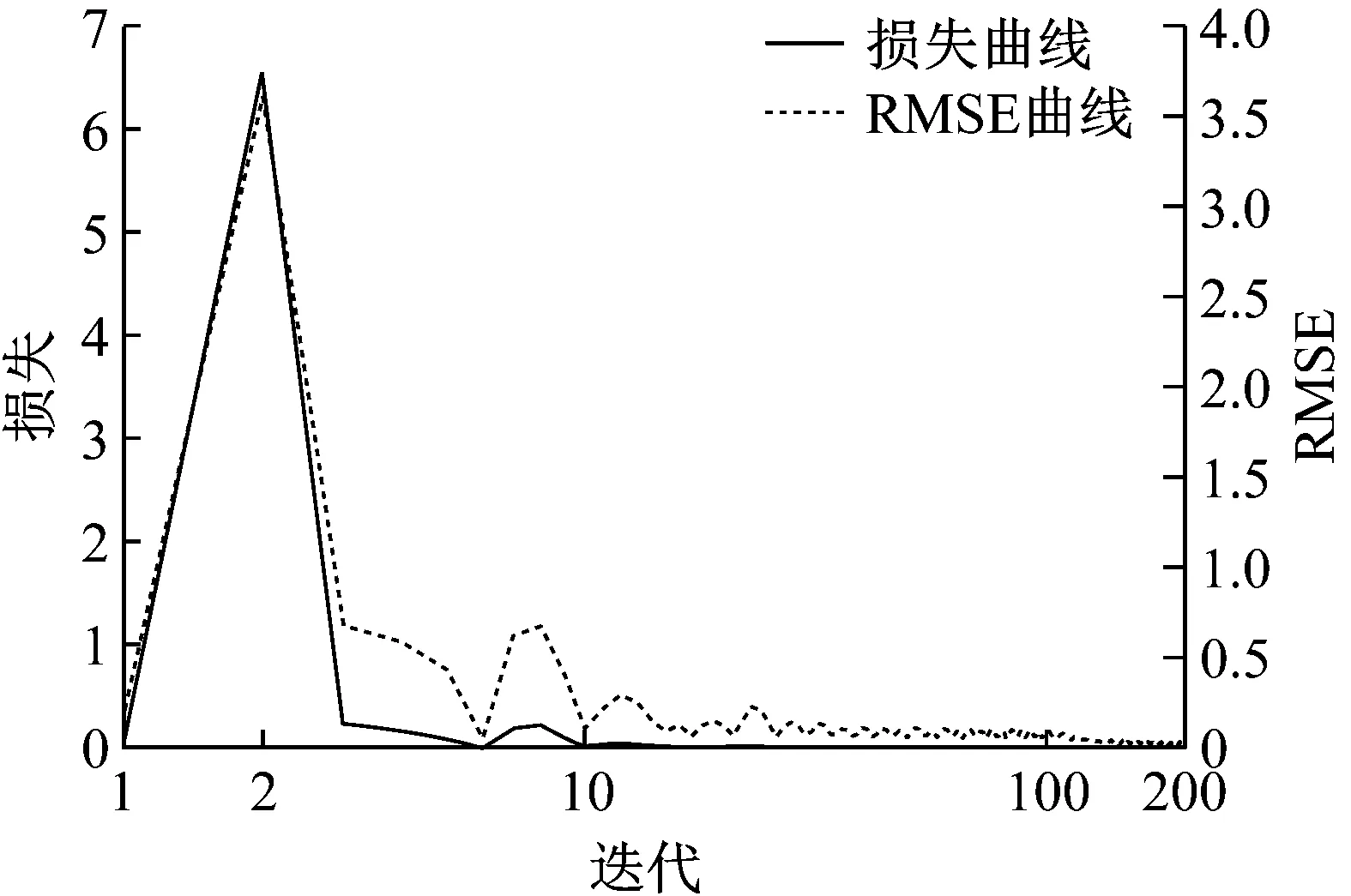
图3 神经网络训练进度图Fig.3 Neural network training progress chart

由于本文使用RLS递归最小二乘法辅助循环神经网络,将数据交予RLS算法先行计算,再输入神经网络计算,故降低了网络的初期计算难度,优化了网络模型初始化权重,在训练刚开始时,网络较好训练,损失曲线起点较低(图3),从第二次迭代开始损失曲线与RMSE曲线急剧上升,说明网络训练初期多次寻找最佳拟合方式导致进度缓慢,前期计算均方根误差较大,第3～6次损失曲线与RMSE曲线急剧下降证明网络训练初步拟合成功,计算出的均方根误差逐渐变小。但是由于输入多组不同的训练信号数据,第6次迭代后初次拟合与部分数据不匹配,导致损失曲线和RMSE曲线出现第二峰值,随后根据前一次的拟合进行修改再拟合直到拟合结果与所有数据均相匹配为止。通过网络训练损失曲线和RMSE曲线可以看出,当迭代次数达到200次时,损失曲线达到零值,RMSE曲线降低至0.000 03,并趋于稳定,说明此时网络已经完成训练。

3 自适应滤波试验分析

选取网络训练中使用的Kobe波、Trinidad波和Chi-Chi波作为无噪原始波,通过MATLAB编程软件中awgn函数和rand函数向信号中随机叠加高斯白噪声信号,形成仿真含噪信号。awgn函数语法为Y=awgn(x, SNR, signalpower),其中x为原始波信号,SNR为信噪比大小,单位是dB, signalpower为以dBW为单位的原始波信号功率;rand函数语法为M=rand,生成一组随机数组M。将随机数组M代入awgn函数中的SNR即可生成随机仿真含噪信号。分别使用训练后的RNN自适应滤波法以及USGS滤波法对试验集数据进行处理,得到原始波、自适应滤波、USGS滤波对比图形,如图4所示。

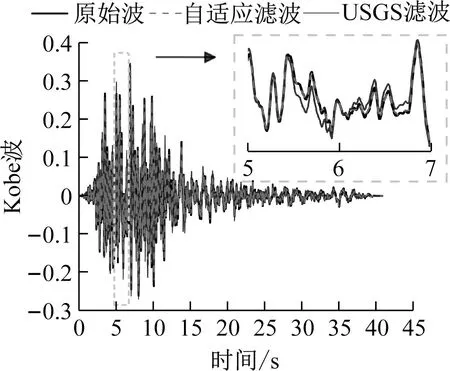
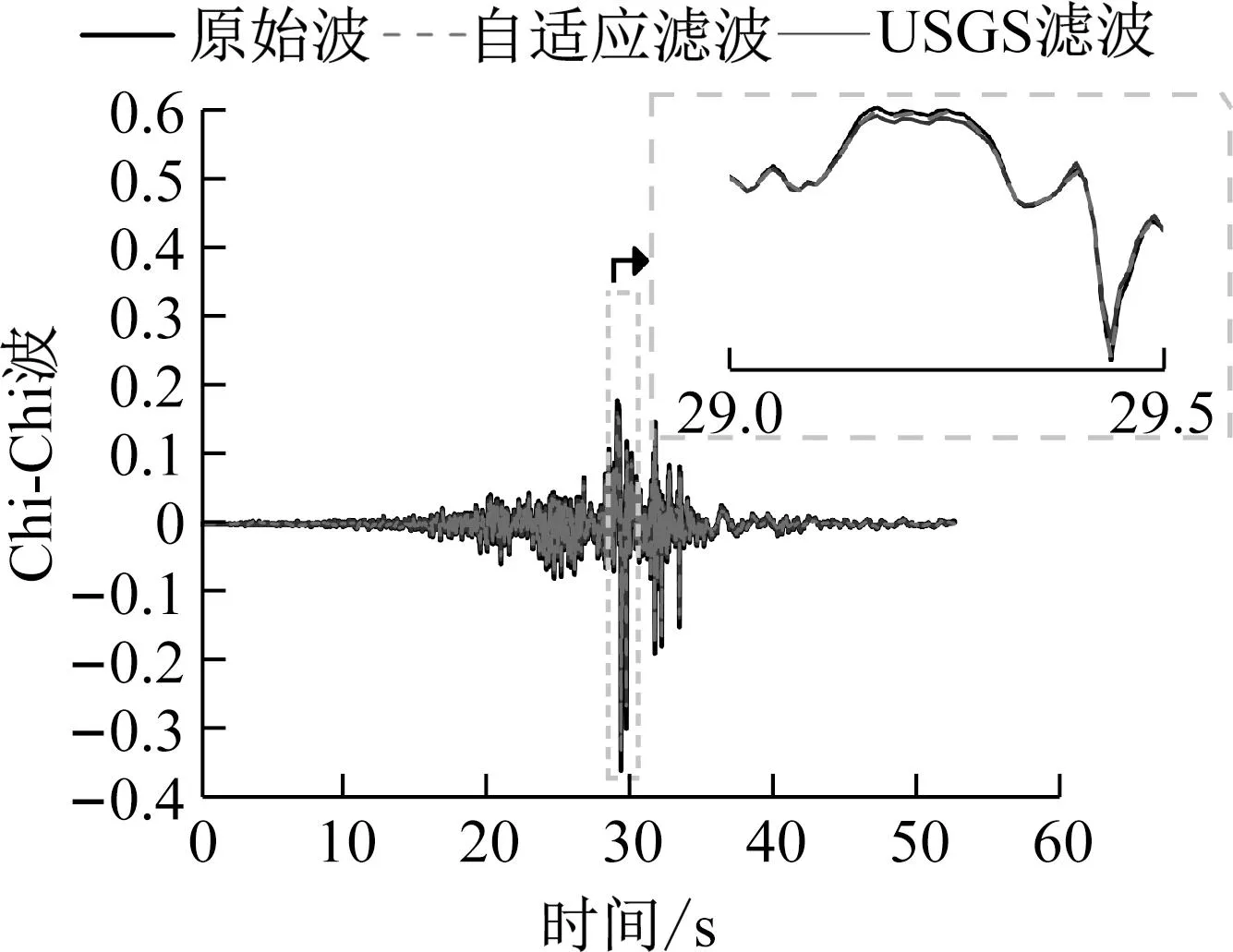
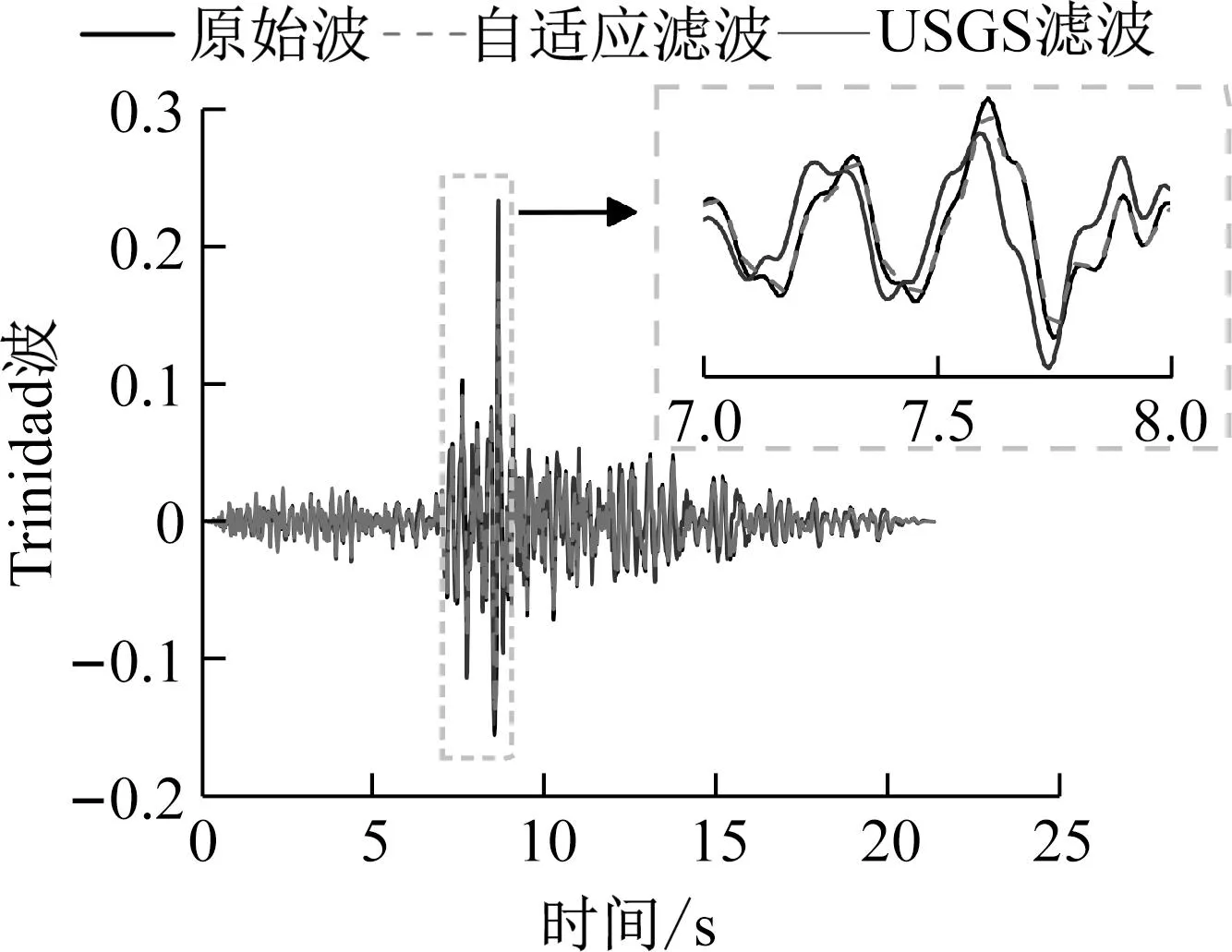
图4 Kobe波、Chi-Chi波、Trinidad波滤波后的加速度时程记录比较Fig.4 Comparison of Kobe waves、Chi-Chi waves and Trinidad waves filtered acceleration time history records

由图4可知,通过对比自适应滤波法滤波后波形、USGS滤波法滤波后波形、原始波形使用自适应滤波法对Kobe波、Trinidad波和Chi-Chi波的波形进行处理后,曲线连续、平滑,与原始波形契合度较高,具有更好稳定性;而使用USGS滤波法滤波后,Kobe波出现了信号失真现象,Trinidad波和Chi-Chi波的波峰出现尖刺问题。由此可见,RNN自适应滤波法相较于USGS滤波法在滤波过程中对地震加速度信号有更强的分析辨别能力,在滤波后更贴近原始波形。

4 不同滤波方法比较

4.1 滤波准确率对比

通过滤波试验分析可以看出RNN自适应滤波法较USGS滤波法具有一定的优势,为了从客观方面验证RNN自适应滤波法在地震滤波方面的精度,本文采用计算均方根误差对数据进行量化分析,其公式为

(16)

式中:n为观测次数;Xobs,i为滤波后数值;Xmodel,i为原始数值。RMSE的值越小,滤波的准确度越高,表1为两种方法滤波后的RMSE。

表1 两种滤波法的RMSE对比Tab.1 Comparison of RMSE between two filtering methods

由表1可知,RNN自适应滤波法相较于USGS滤波法,Kobe波滤波误差降低了0.14%, Trinidad波滤波误差降低了6.05%,Chi-Chi波滤波误差降低了3.50%,并且RNN自适应滤波法处理地震波后的平均准确率达到93.37%,较USGS滤波法高出6.63%,说明在地震波信号处理结果中,RNN自适应滤波法处理后的波形与原始波形还原率较高,具有更强的适应性。

为了验证在不同噪声下,两种滤波处理方法的适应性,选取Chi-Chi波作为原始波形,在10 Hz、20 Hz、40 Hz随机噪声加载下生成100组测试数据,其中10 Hz占25组,20 Hz占35组,40 Hz占40组。将100组测试数据随机分布并在同一时间开始滤波测试,比较两种方法的滤波准确率以及滤波速度,测试结果如图5和表2所示。

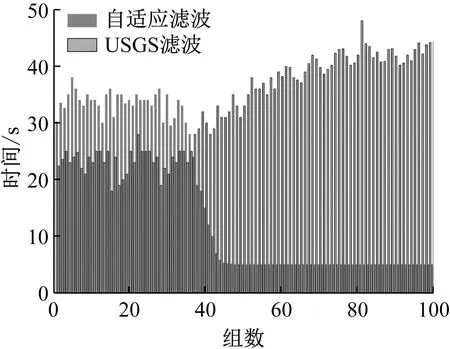
图5 2种滤波法的速度对比Fig.5 The velocity comparison of two filtering methods

表2 各噪声下2种滤波法的准确率对比Tab.2 Comparison of accuracy between two filtering methods under different noises

由图5可知,前36组USGS滤波速度高于自适应滤波,在第36组后自适应滤波速度迅速提升最终达到5 s左右即可滤完一组,而USGS速度逐渐下降,最慢甚至达到48 s滤完一组。由表2可知,通过训练两种方法在无噪声状态下均能较好反馈原始波形,当加入噪声后,由于噪声湮灭了一部分原始数据特征,导致准确率下降。但是RNN自适应滤波法相比于USGS滤波法的准确率下降程度较小且能够保持较高的准确率。

结合表1、表2以及图5发现两种滤波方法在处理大量数据时,USGS法滤波结果精度较低,滤波速度随着组数增加逐渐降低,而自适应滤波法在滤波结果精度较高的前提下,依然能够保持高效的滤波速度。两种方法对比得出,不论是滤波速度还是滤波精度,自适应滤波法均优于USGS滤波法。

4.2 实际地震波滤波效果对比

为进一步证明自适应滤波方法在不同类型场地条件应用方面的优越性,本文选取美国太平洋地震研究中心PEER数据库中不同场地类别观测台阵的地震记录[19](如表3所示),对比了两种不同滤波方法在五种不同场地类型[20]的含速度脉冲近场地震记录的滤波结果。可以看出自适应滤波和USGS滤波在C、D、E场地的滤波结果差异显著(如图6所示)。在A、B场地中自适应滤波和USGS滤波均有较好的结果,但是USGS滤波结果存在明显的峰值尖刺,而自适应滤波结果没有表现出异常峰值。在C、D、E场地中,USGS滤波结果出现相位提前以及压缩峰值过度导致信号丢失现象,自适应滤波法在滤波的过程中能够最大程度地保留地震信号的原始波形。通过实际地震记录的滤波结果可以看出自适应滤波法明显优于USGS滤波法。

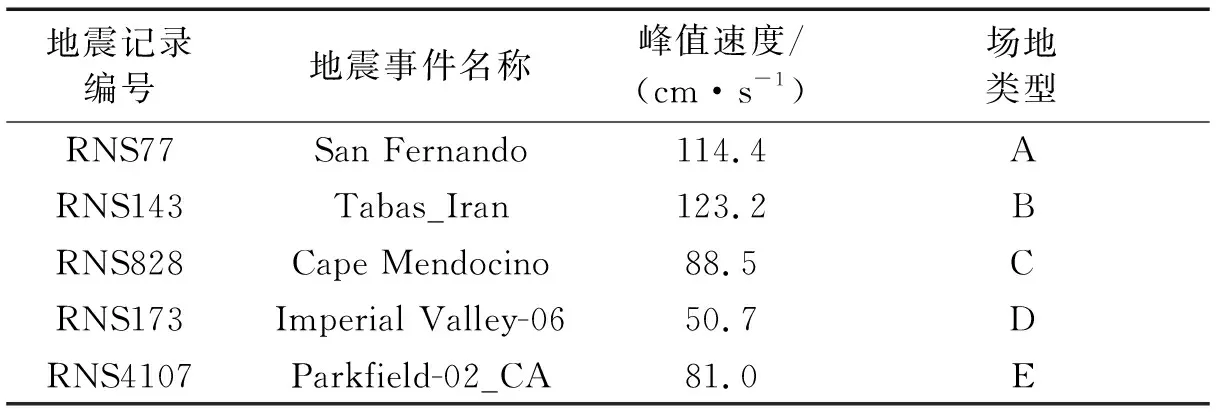
表3 含速度脉冲近场地震记录Tab.3 Near-field seismic records containing velocity pulses

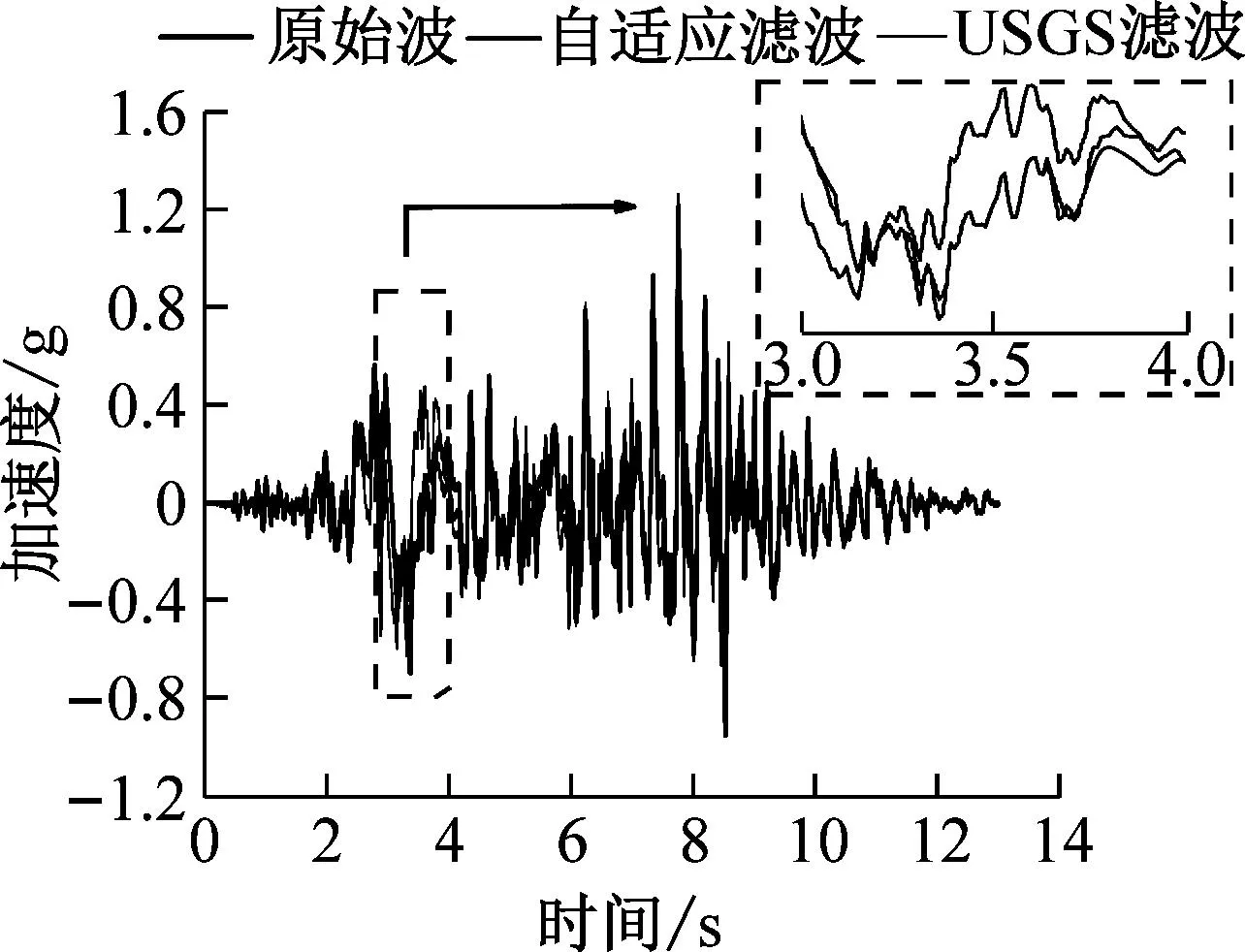
(a) A场地

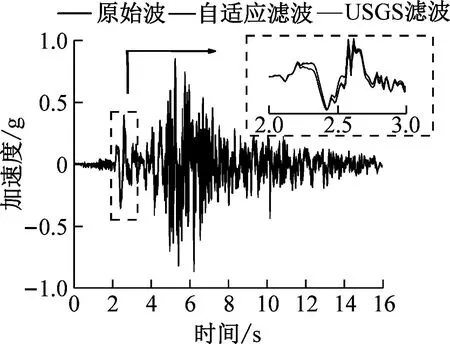
(b) B场地

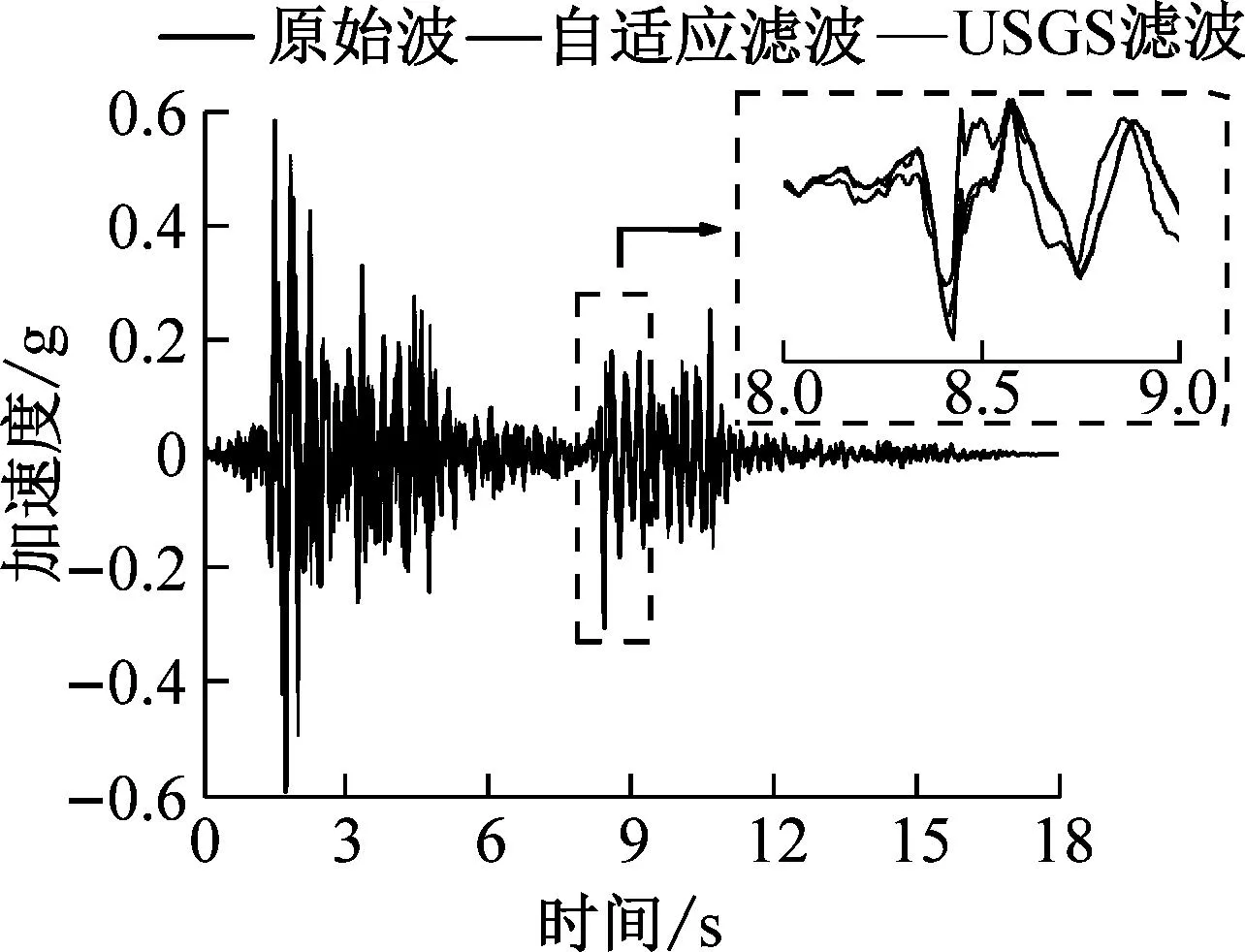
(c) C场地

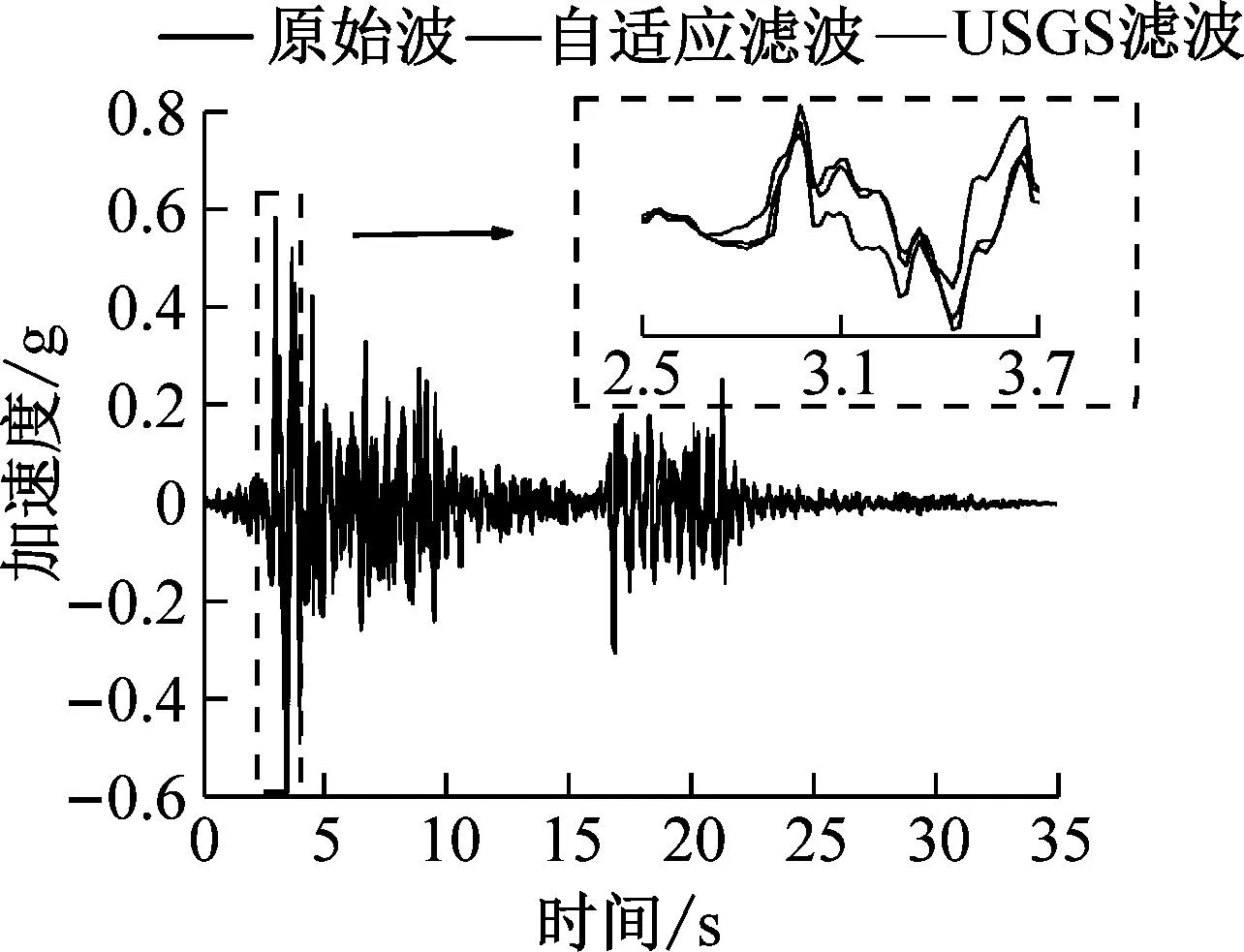
(d) D场地

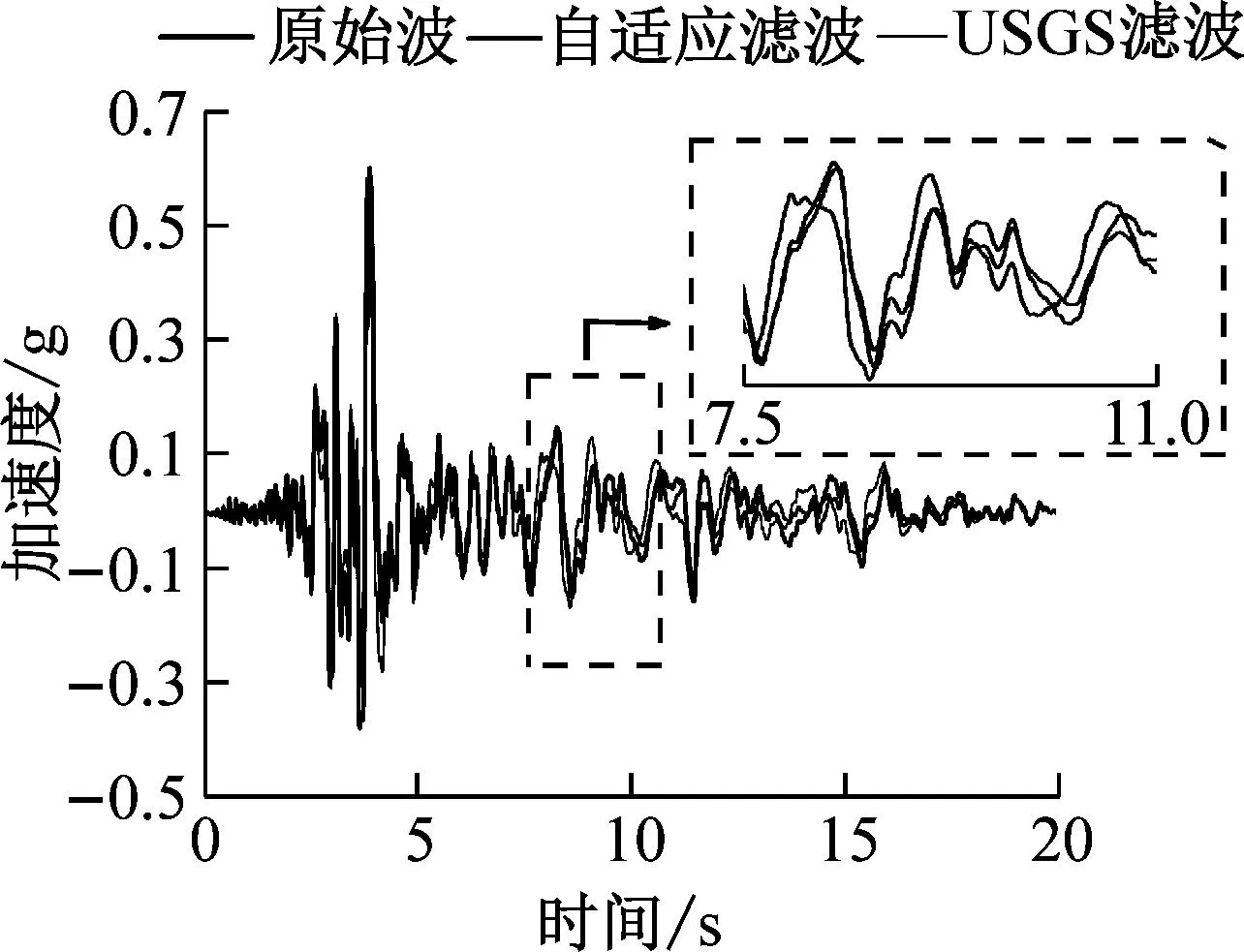
(e) E场地图6 A、B、C、D、E场地速度脉冲近场地震记录滤波结果Fig.6 A,B,C,D,E field velocity pulse near field seismogram filtering results

5 结 论

地震信号的滤波是目前岩土模型试验和数值模拟中的关键步骤,本文介绍了一种基于循环神经网络的自适应滤波方法,为研究地震动响应开拓了一种新的思路。通过与目前公认度最高的USGS滤波法进行比较验证本方法的有效性,主要结论有:

(1) 循环神经网络(RNN)在处理多条时间序列数据的速度呈现上升的趋势。本文提出的循环神经网络充分结合RLS算法的自匹配滤波阶数与数据筛选,降低传统人为干扰、经验参数、单一校正等因素的影响,提高了循环神经网络数据序列的处理速度。

(2) 递归最小二乘法(RLS)的加入对于滤波的速度和精准度有显著影响。本文的RLS算法通过引入遗传因子和先验估计误差向量,对于复杂的时间序列数据进行预处理, 防止训练网络时出现梯度爆炸现象,提高RNN神经网络滤波速度和精度。

(3) 自适应滤波方法能够更大程度还原原始地震波形,保证数据的完整性和准确性。通过训练后的自适应滤波法在处理多条复杂的地震波时所展现的准确度远高于传统USGS滤波法,大幅度降低了滤波阶数以及滤波频率对结果的影响,在不同频率噪声干扰下自适应滤波法能够保持更好的滤波效果,为地震工程研究提供更为真实的记录数据具有重要的参考价值和工程意义。