面向电磁水声换能器的高静低动型悬架动力学研究

孙士涛, 么宇辉, 张 希, 李鸿光

(上海交通大学 机械系统与振动国家重点实验室,上海 200240)

产生声波信号的电磁水声换能器作为声呐的核心部件,现已被广泛应用于海洋资源开发及水声通信等领域。目前电磁水声换能器的研究焦点主要集中在低频、宽带、小尺寸、大功率和深水工作等方面[1-4]。

电磁换能器利用电场与磁场之间的相互作用产生驱动力推动辐射面振动产生低频声波。目前使用广泛的电-磁式换能器主要有英国研制的UW350、UW600及美国研制的G34、J11等[5-6]。桑永杰[7]研制的电磁换能器以小尺寸实现了宽带发射,诸多学者对电磁换能器的各部件进行了优化设计以提升辐射声源级,雷云中等[8]基于声学超材料等效零质量特性设计了一种超结构的辐射盖板使换能器获得了较高的辐射声压级;杨洋等[9]验证了声腔结构及声腔内气体参数对声源级曲线起伏的影响。唐良雨[10]推导了两根线圈分开绕制和使用同一根导线绕制的驱动力计算公式。

电磁换能器的谐振频率与振动系统的悬架弹簧刚度、振动质量等参数密切相关。通过采用柔性大的弹簧,可以将谐振频率控制在几十赫兹的范围内。在超过谐振频率的频段上,换能器的声压响应级曲线平坦,可实现多个倍频程的宽带声发射。该类换能器具有工作频率极低、频带宽和体积小等优点,因此在小尺寸、超低频发射换能器领域具备独特的优势[11]。但由于其弹簧柔性很大,为保证其工作在平衡点附近,需单独设计压力补偿装置使换能器内外压力平衡。

随着工作深度的增加,换能器受到的静水压力逐渐增大,因此需在换能器内设置压力补偿装置,以保持内外腔的压力平衡。电磁换能器工作在深水环境下,通常可以采用压缩换能器内腔气体方式实现压力补偿。然而,由于换能器内部声腔结构的存在,声源级理论设计结果与实测结果存在较大差别[12],此外,内腔高压气体也会引入非线性附加刚度,使系统变得复杂,谐振频率增大,并且可能导致安全问题的产生[13]。

为解决上述问题,本文拟采用具有高静低动刚度特性的悬架装置替换原线性悬架,使系统具有较低的谐振频率的同时还有较大静承载能力,保持良好的工作性能。在此背景下,高静是指具有较高的静承载能力以承载静水压力,低动是指在工作位置附近系统具有较低的动态刚度,目前对高静低动装置的研究,多在非线性隔振方面。自Carrella等[14]首先提出高静低动概念以来,发展至今已产生多种构型,如三弹簧结构[15]、欧拉屈曲梁[16]、曲面-弹簧-滚子结构等[17-20]。

本文首先对现有电磁换能器进行了线性系统建模,其次,介绍了高静低动刚度特性的原理,对引入高静低动刚度特性的系统进行建模。再次,提出一种可定制凸轮廓线的“凸轮-弹簧-滚子”装置设计方法,实现预期的高静低动刚度;然后,通过数值仿真,探究了引入高静低动刚度特性前后,系统声源级和谐振频率的变化,探讨了不同输入电压对系统特性的影响;最后进行原理性试验验证,通过锤击试验法得到高静低动刚度型悬架固有频率低于相应的线性悬架,验证了在悬架中引入高静低动刚度可使换能器获得更低的谐振频率和更高的声源级。

1 系统模型

1.1 线性系统模型

电磁水声换能器机械结构示意图如图1所示。辐射板、悬架弹簧、线圈为运动部件,永磁体、软磁体与外壳固连,忽略密封件、导向装置等。当线圈两端接入交变电压产生交变电流时,线圈在永磁体与软磁体组成的磁回路中受到安培力作用沿轴线方向往复运动,带动辐射板推动周围水介质将机械能转化为声能辐射出去。

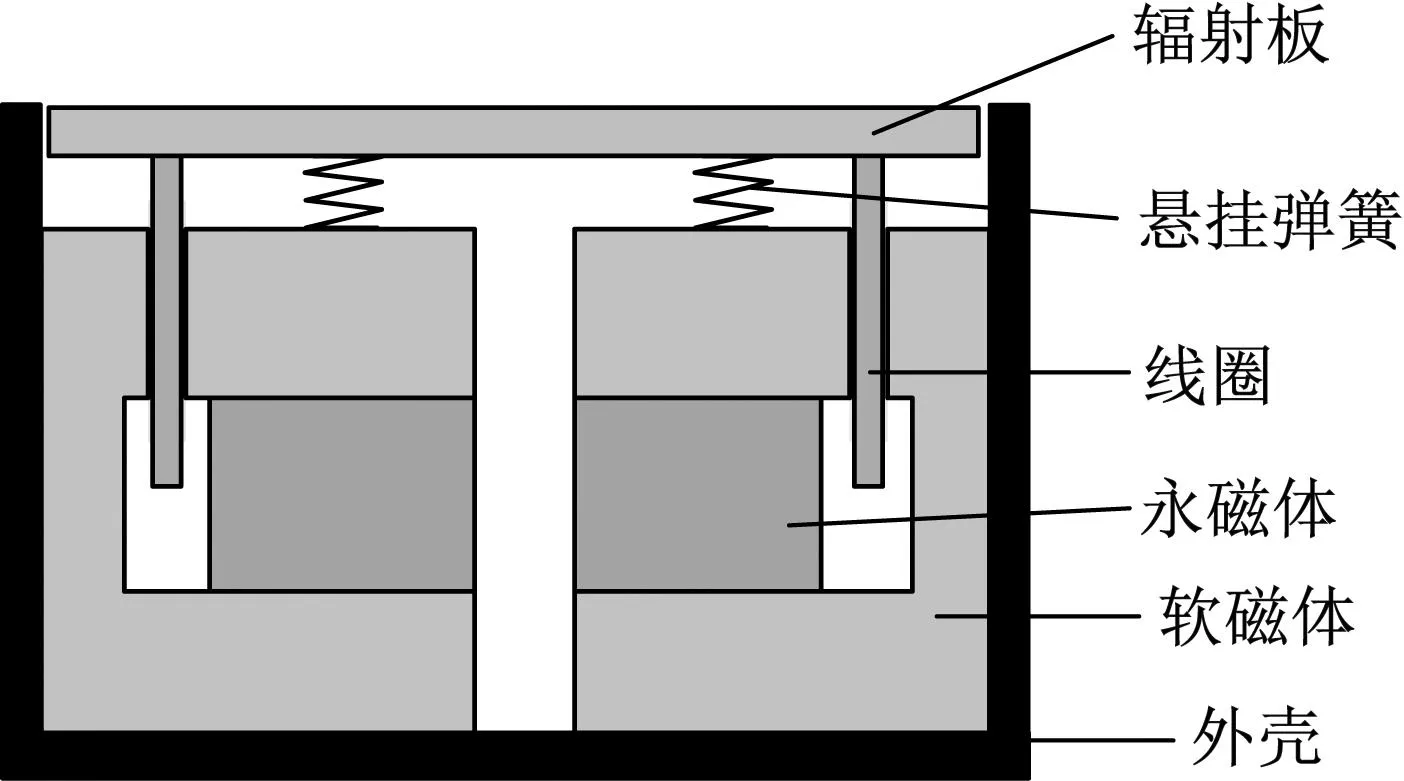
图1 机械结构示意图Fig.1 Schematic diagram of mechanical structure

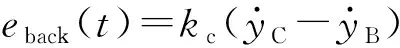
(a) 系统机械振动模型

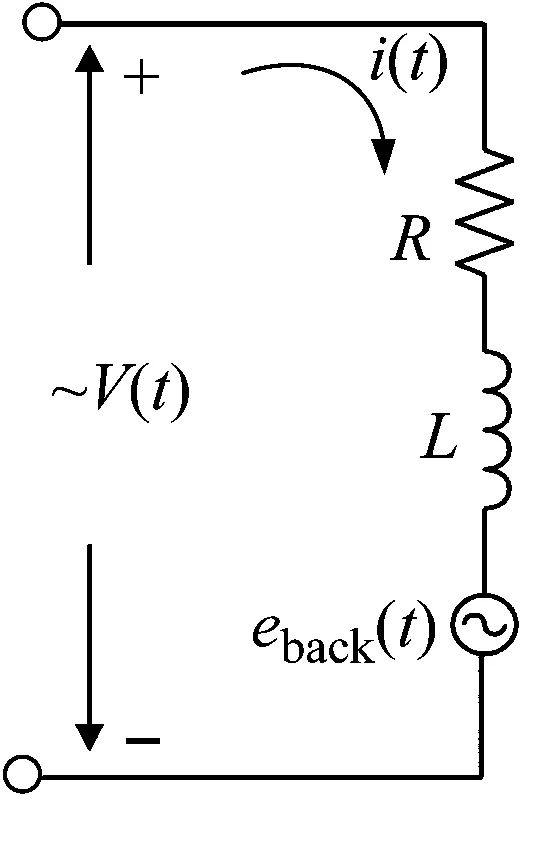
(b) 系统电气简化图图2 线性系统模型Fig.2 Linear system model

对图2所示线性系统模型,根据牛顿第二定律和基尔霍夫定律,分别对各质量块和动态电路建立微分方程,得到:

KC(yT-yC)+KS(yT-yB)=0

(1)

(2)

(3)

(4)

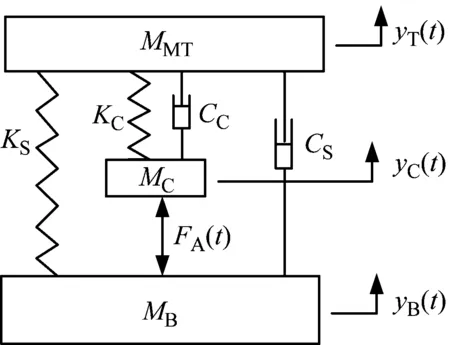
式中,kc为机电耦合系数。FA(t)=kci(t)为线圈受到的安培力。

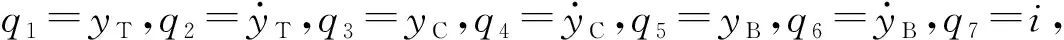
(5)

其中:

(6)

采用四阶龙格库塔方法求解此微分方程组,可求得在不同频率下辐射板中心振速的响应。

1.2 高静低动系统模型

本文拟将高静低动非线性刚度引入换能器的系统模型中,使线性系统变为高静低动非线性系统。高静低动系统多由正刚度机构与负刚度机构并联而成,其力-位移曲线为变刚度曲线,如图3虚线所示。其中,具有正刚度特性的机构的力-位移曲线如图3点线所示,具有负刚度特性的机构力-位移曲线如图3点画线所示。采用线性弹簧作为悬架的线性系统的力-位移曲线如图3实线所示。当辐射板所受静水压力为Fc时,高静低动系统产生静变形量y0到达平衡位置,在y0附近区间内工作时,切线斜率较线性系统小,表明其动态刚度较小。

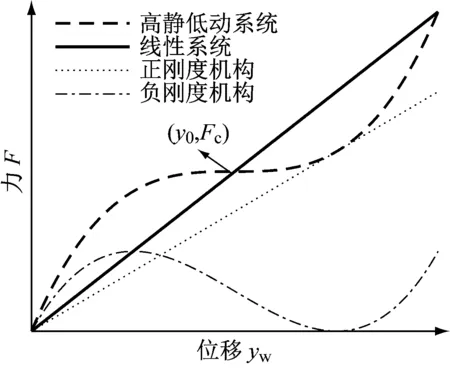
图3 高静低动原理示意图Fig.3 Schematic diagram of high-static-low-dynamic principle

将具有高静低动刚度特性的悬架应用在换能器中替代原辐射板与软磁体等之间的线性悬架,保持电气系统不变,得到新的系统力学模型如图4所示,图中KHDLS表示高静低动刚度特性。

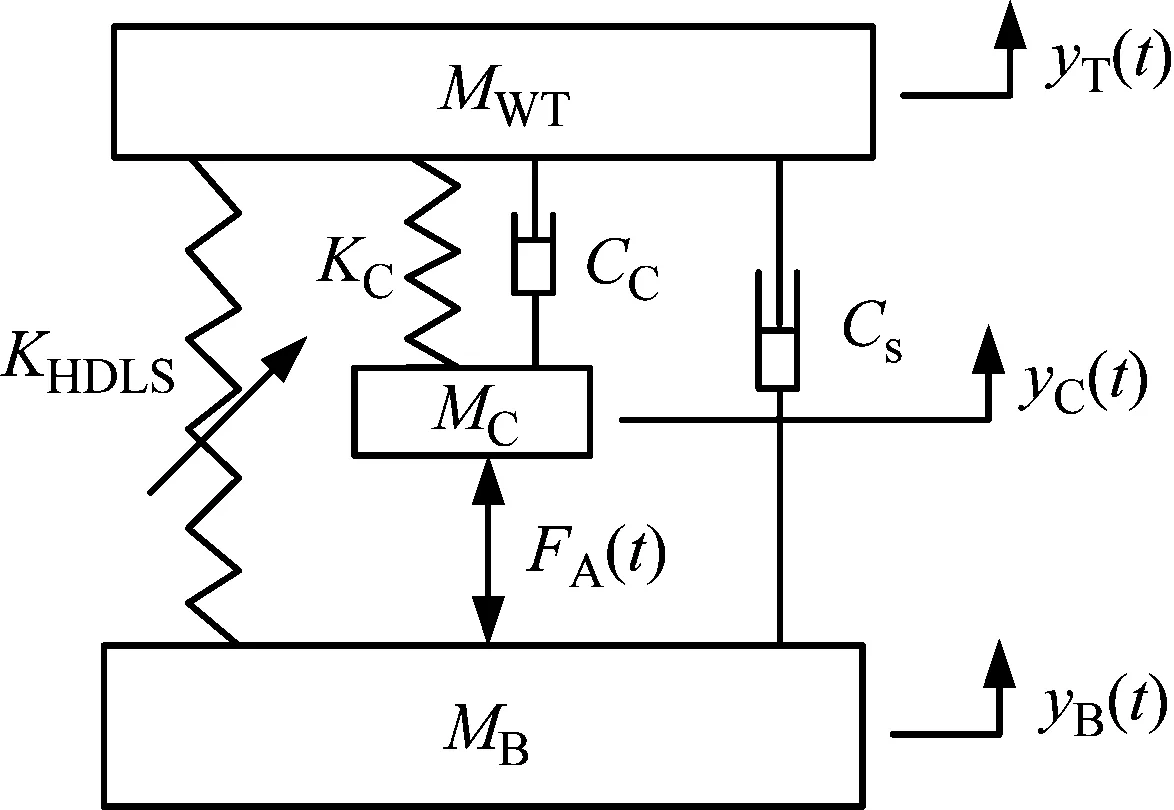
图4 高静低动系统力学模型Fig.4 Mechanical modeling of high-static-low-dynamic systems

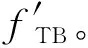
(7)

式中:

(8)

采用数值方法求解此微分方程,即可求得该高静低动系统的三个质量块在不同频率下的频率响应。

1.3 凸轮-弹簧-滚子装置

本文设计“凸轮-弹簧-滚子”装置实现高静低动刚度特性,将其应用在换能器中,换能器结构示意图如图5所示。

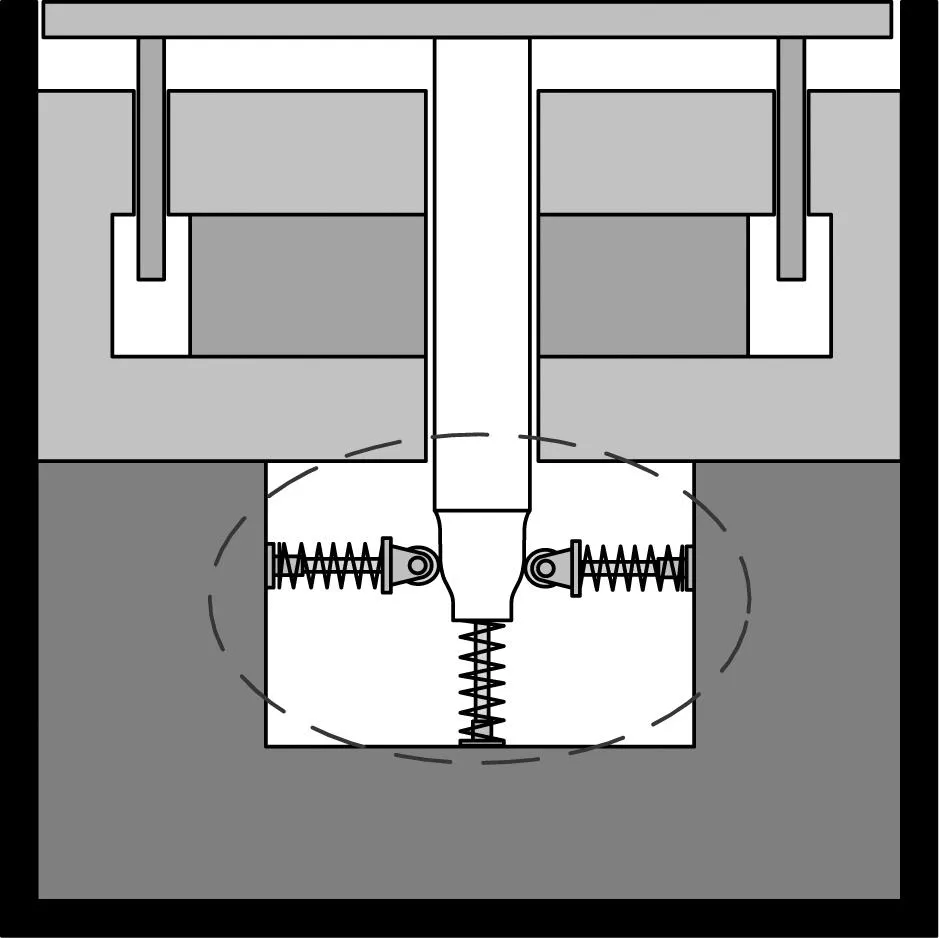
图5 换能器结构示意图Fig.5 Schematic diagram of transducer structure

“凸轮-弹簧-滚子”装置的示意图如图6所示,包括凸轮、竖置弹簧、横置弹簧、滚子、线性轴承等。在力F作用下凸轮在竖直方向上的位移为yw;kv为竖直弹簧刚度系数,提供竖直方向上的正刚度;kh为横置弹簧刚度系数;r为滚子半径滚子与凸轮轮廓作用提供竖直方向上的负刚度。

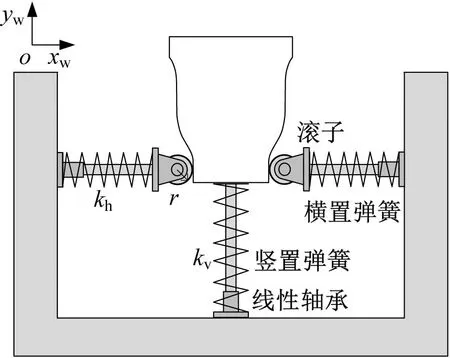
(a) 空载状态

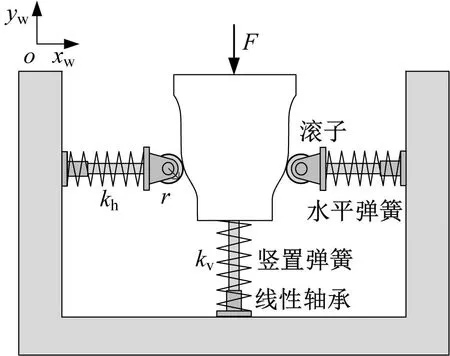
(b) 受力状态图6 凸轮-弹簧-滚子结构示意图Fig.6 Schematic diagram of cam-spring-roller structure

由图3可知,为使“凸轮-弹簧-滚子”装置实现预期的高静低动力-位移曲线,可给定正刚度机构的力-位移曲线方程,得到需要设计的负刚度机构力-位移曲线方程,进而求解满足负刚度机构力-位移曲线方程的凸轮轮廓曲线即可。

如图6所示,该装置为关于竖直中心线左右对称结构,滚子与横置弹簧及线性轴承均为对称布置,因此,在进行凸轮轮廓求解时,只对右半边轮廓进行求解,再通过对称原则即可得到完整的凸轮轮廓线。

在外力F作用下,“凸轮-滚子”机构右半部分凸轮和滚子的受力分析图如图7所示。由于凸轮与滚子之间为滚动摩擦,故分析时忽略了此处摩擦力。图7(a)为凸轮的受力分析图。

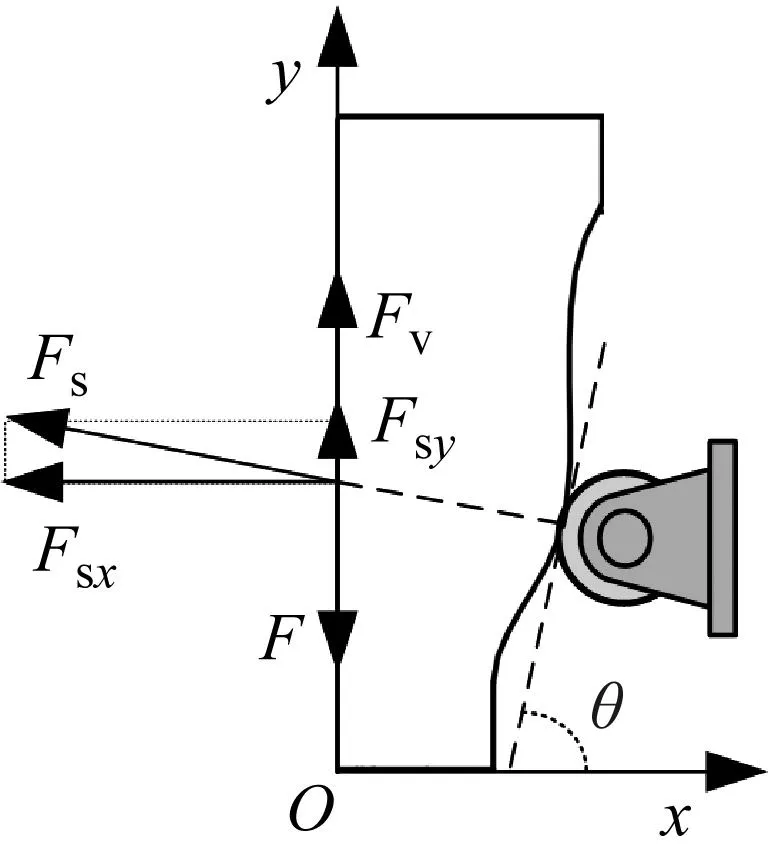
(a) 凸轮

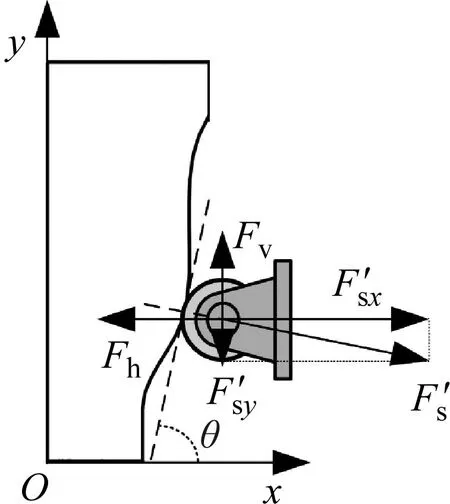
(b) 滚子图7 凸轮-滚子结构受力分析图Fig.7 Force analysis diagram of cam-roller structure

当力F作用在竖直方向(yw轴)上时,凸轮在yw轴方向上的受力平衡方程为

Fv+2Fsy-mg-F=0

(9)

Fv=kv(y+Δy)

(10)

Fsy=Fscosθ

(11)

式中:Fv为竖置弹簧回复力;Δy为竖置弹簧预压缩量,满足kvΔy=mg;Fs为凸轮与滚子之间的相互作用力;θ为凸轮与滚子接触点处凸轮轮廓的切线与水平方向的夹角;Fsy为凸轮与滚子之间的相互作用力在竖直方向上的分力;F=φ(yw)为预期已知的力-位移函数。

如图7(b)所示为滚子的受力分析图,滚子的受力平衡方程为

(12)

Fh=khx

(13)

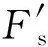
联立式(11)和式(12)可得到Fh与Fsy之间的关系为

(14)

假定滚子半径很小,可当作尖顶从动件进行分析,则接触点处的斜率凸轮轮廓曲线的斜率为

(15)

当横置弹簧存在预压缩量δ时,Fh的表达式为

Fh=kh(x+δ)

(16)

将式(14)和式(16)代入式(15)中,可以得到关于Fh和Fsy之间的微分方程

(17)

通过式(17)发现,只要得知Fsy的变化规律,并求解式(17)就可以得到凸轮右半部分的理论轮廓曲线,因此根据水声换能器的实际工况需求,设计Fsy的变化曲线,就可以实现在设计区间内实现最佳的驱动效果。

在实际求解过程中,采用数值法求解(17)的微分方程,从而简化计算。需要注意的是,上述方法得到的为凸轮的理论轮廓线,由于滚子半径不可忽略,所以还需进一步求解其凸轮的实际轮廓线。

如图8所示,设点A(x,y)为滚子中心,点A位于迹线(也即凸轮理论轮廓线)L上,假设该迹线方程为

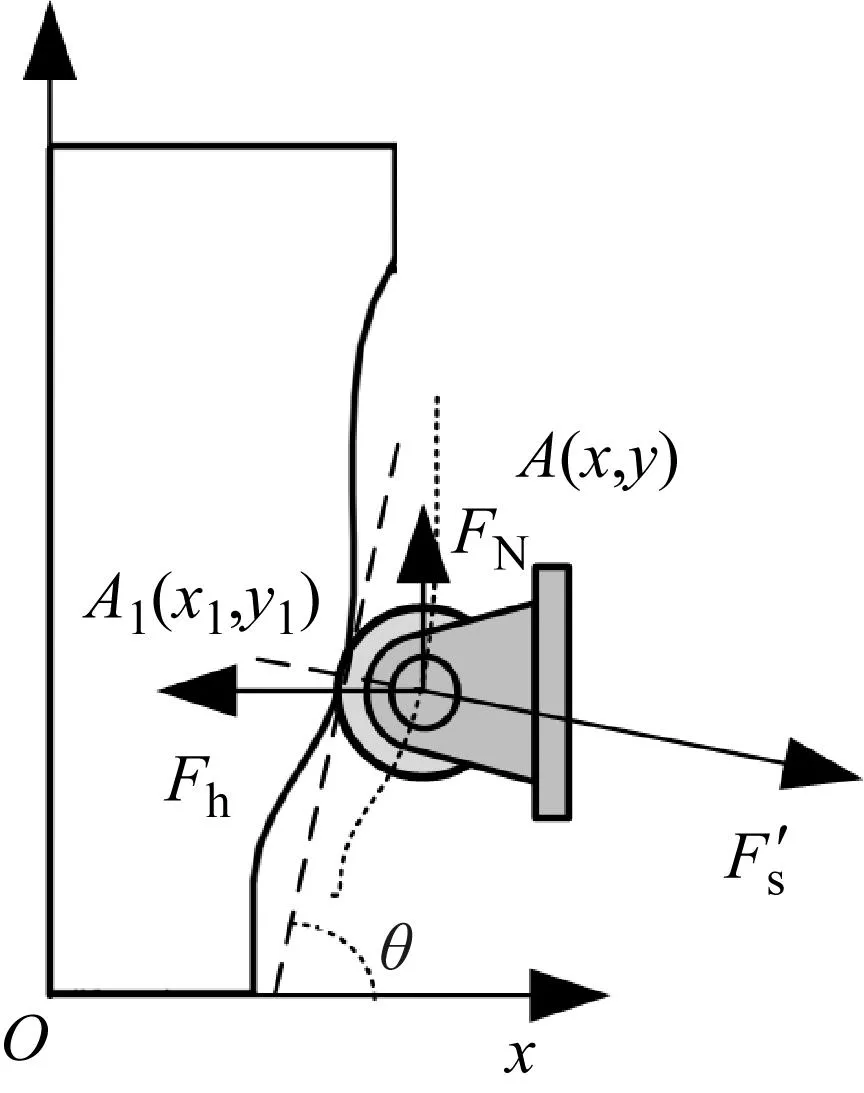
图8 凸轮实际轮廓线下的受力分析Fig.8 Force analysis under the actual contour of cam

L=f(x,y)

(18)

则与之对应的凸轮与滚子的接触点A1(x1,y1)位于凸轮实际轮廓线L1上。已知滚子半径为r,则A1点的坐标为

(19)

将式(19)代入式(18)中,可以得到凸轮实际轮廓曲线方程

L1=f(x1+rsinθ,y1-rcosθ)

(20)

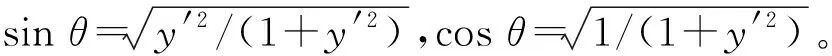
使用数值积分求解式(17)和式(20)即可求得凸轮实际轮廓曲线。最后通过对称性即可得到完整的凸轮轮廓曲线。

2 系统性能评估与动力学仿真

2.1 性能评估指标

评估发射换能器的指标有谐振频率、发射电压响应级、声源级等。对于发射换能器,一般要使其工作在谐振频率上以获得更高的声输出性能。

声源级(source level,SL),定义为离开声源等效中心单位距离(即1 m)处的声压级,用于描述换能器所发射的声信号的强弱[22],表示为

(21)

式中:pref为基准声压,pref=10-6Pa;pRMS为所测声波的有效声压。

在超低频频段工作的声源尺寸通常远小于水中声波的波长,因此可将声源作为脉动球来进行分析。考虑到电磁换能器在超低频工作时,波数远小于1,则距离脉动球声中心等效距离为1 m处的声压的幅值大小计算公式可简化[23]为

(22)

式中:ρ为介质密度;X为体积位移。

2.2 动力学仿真

对原线性系统与应用了“凸轮-弹簧-滚子”装置做悬架的高静低动系统进行仿真,仿真参数如表1所示。仿真频率范围为1～1 000 Hz,求解获得系统在相同的激励电压下,应用不同的凸轮-弹簧-滚子装置前后的换能器系统声源级相对值(取依据表1参数按照式(21)和(22)计算所得的线性系统声源级的最小值为参照值)进行对比。

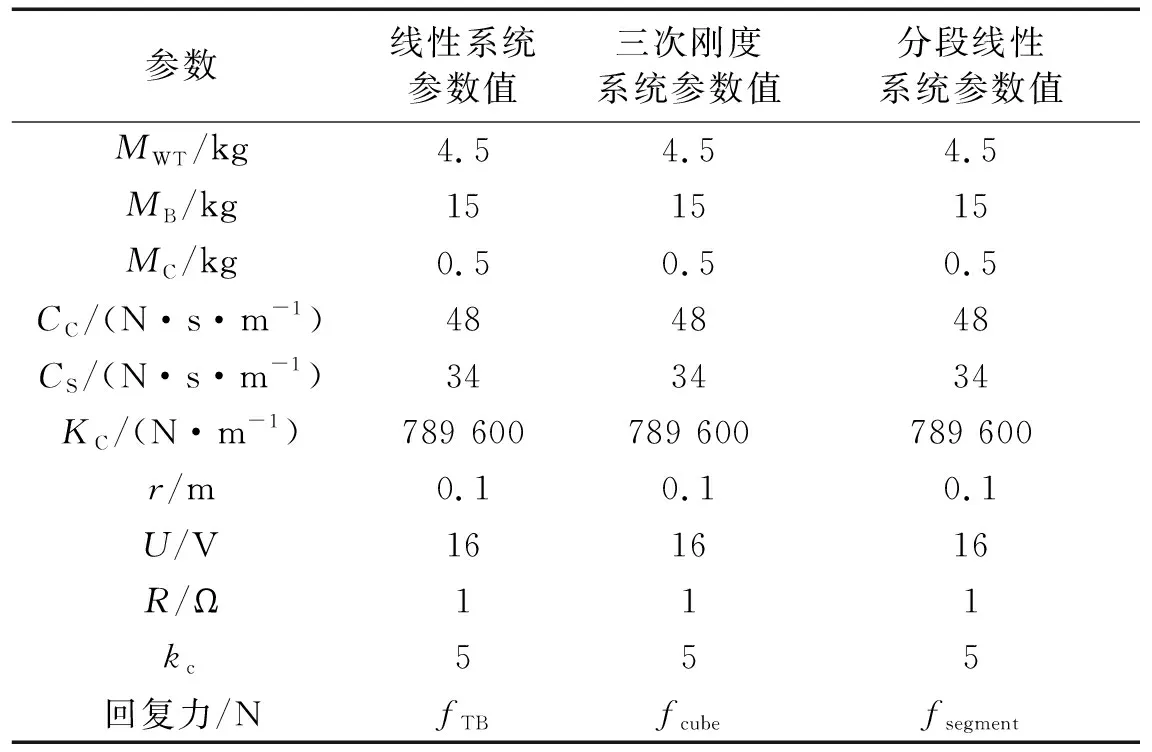
表1 系统仿真参数Tab.1 System simulation parameters

根据回复力函数的形式不同,将采用线性弹簧做悬架的换能器系统记作线性系统,将采用“凸轮-弹簧-滚子”装置做悬架,且回复力函数为位移立方形式的高静低动系统记作三次刚度系统,将采用“凸轮-弹簧-滚子”装置做悬架,且回复力函数为分段线性形式的高静低动系统记作分段线性系统,仿真探究不同系统之间的差异。

设定为水深25 m处承受静水压力Fc=7 500 N,线性系统悬架静变形量为y0=0.05 m,各系统在达到平衡位置后的换能器系统整体回复力函数如图9所示。

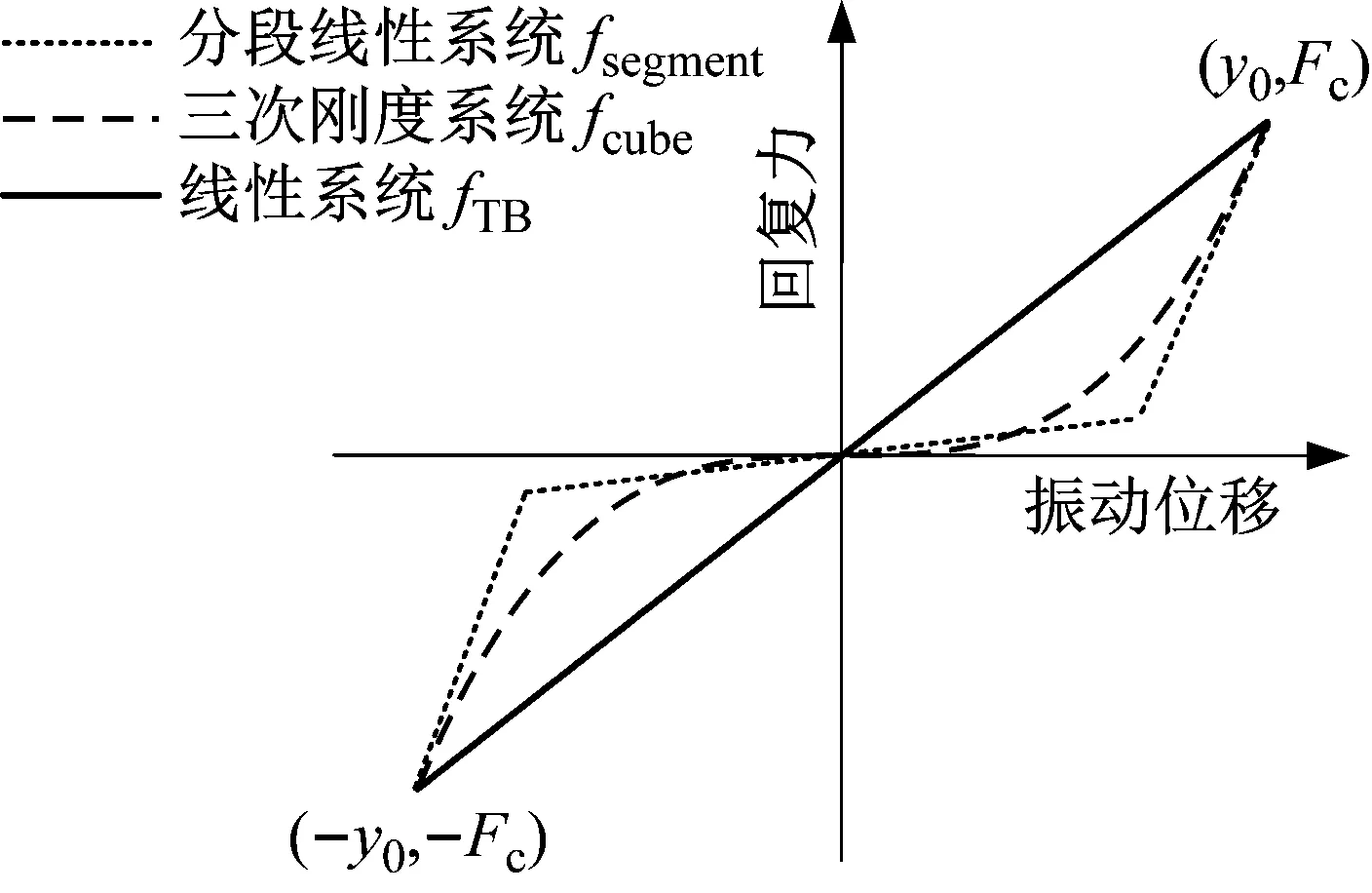
图9 不同系统的回复力曲线Fig.9 Response force curves for different systems

(23)

图10展示了对三系统仿真分析的结果,其中线性系统的两个共振峰峰值点的横坐标依次为31.95 Hz,和211.02 Hz;三次刚度系统两个共振峰峰值点的横坐标为9.86 Hz和211.02 Hz;分段线性系统两个共振峰峰值点的横坐标为7.96 Hz和211.02 Hz。图中各曲线的两个共振频率分别对应两种共振模式。图中第一阶共振频率表示此时辐射板与线圈整体进行振动,第二阶共振频率为210 Hz左右,为线圈在系统中发生共振产生的振动模态,由仿真结果可知,相较于原线性系统,在辐射板与外壳等固定部件之间应用高静低动刚度特性的系统,在极低频区域内(1～20 Hz)声源级增大,在中间频段内(20～100 Hz),高静低动系统的曲线平坦,有利于实现多个倍频程的宽带声发射;在第二阶共振频率点附近(100～300 Hz),高静低动系统的声源级与原系统差异不大;在更高频区域内(300～1 000 Hz),三系统的声源级均呈现下降趋势。

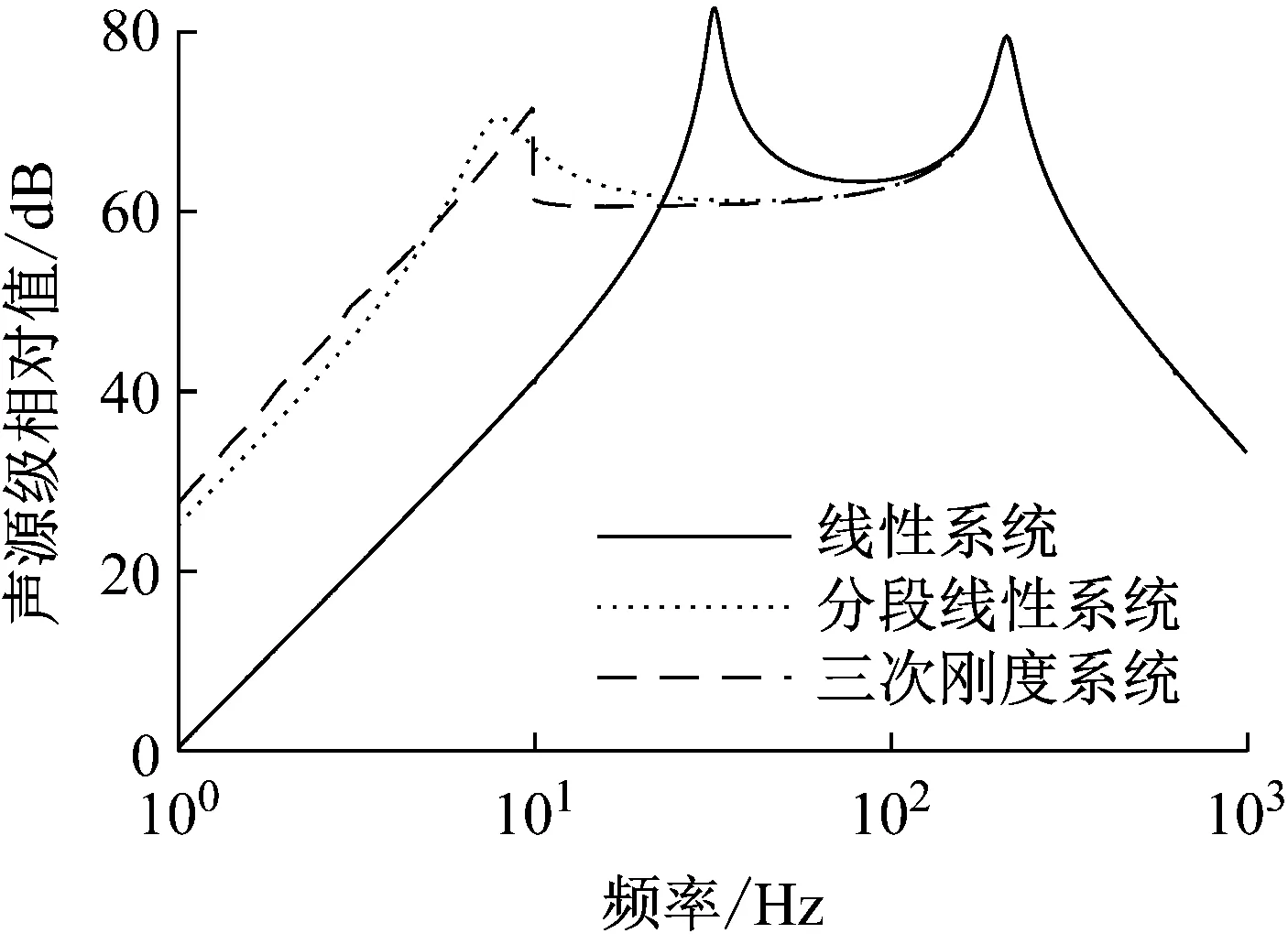
图10 线性系统与高静低动系统的声源级Fig.10 SL for linear systems and high-static-low-dynamic systems

在相同的辐射板表面积与振动频率下,辐射板表面振速与辐射性能正相关,因此随机选取9.86 Hz时线性系统、三次刚度系统及分段线性稳态后1 s内的时域图,比较辐射板板面中心的振速大小,结果如图11所示。在该频率时,线性系统的辐射板振速为0.03 m/s,而三次刚度系统的辐射板振速为0.76 m/s,分段线性刚度系统的辐射板振速为0.56 m/s,在此频率下,三次刚度系统的振速较线性系统提升了约25倍,分段线性系统的振速较线性系统提升了约18倍。

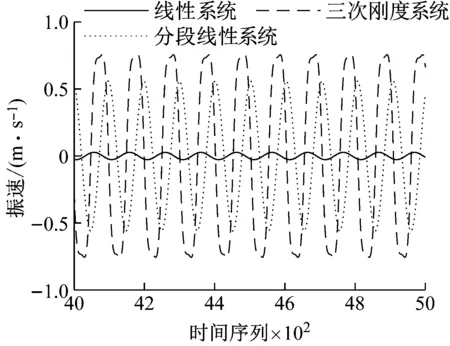
图11 9.86 Hz线性系统与高静低动系统的振速响应Fig.11 Velocity response of linear system and high-static-low-dynamic systems at 9.86 Hz

此外,由图11可看出三次刚度系统的振速波形存在弱非线性,而分段线性系统的振速波形线性特征良好。图12展示了9.86 Hz时三次刚度系统与分段线性系统的稳态解相轨线对比,可以看出,三次刚度系统的稳态解相轨线为腰型,这是因为在工作点位置附近,其刚度是与位移有关的变量,故其相轨线呈现出弱非线性特征。而分段线性系统的稳态解相轨线为椭圆形,说明在低动刚度区间内振动时,分段线性系统相较于三次刚度系统具有良好的线性特征,但最大振速及振幅均小于三次刚度系统,这是由于分段线性系统在较小振幅时,其系统刚度大于三次刚度系统。

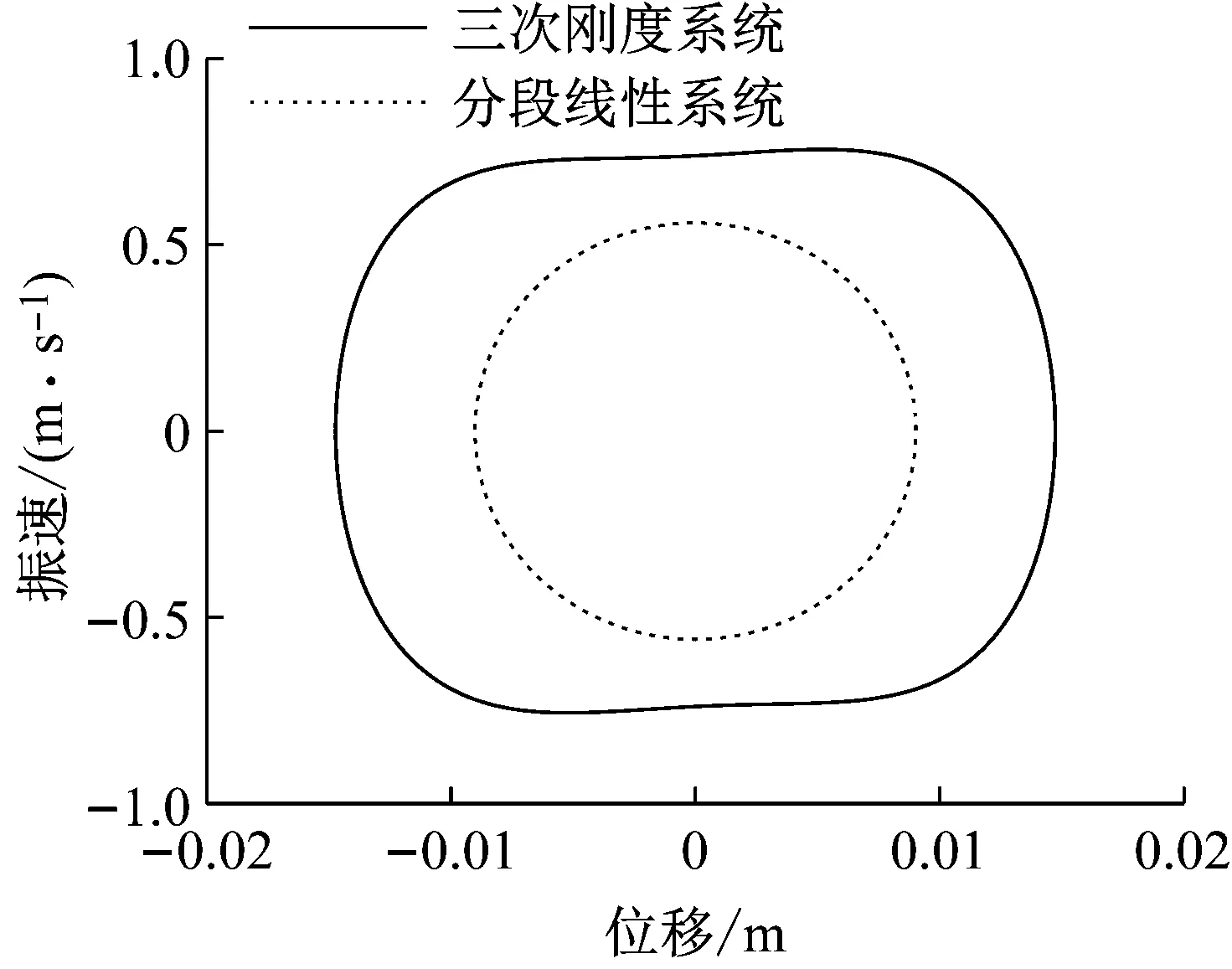
图12 三次刚度系统与分段线性系统稳态解的相轨线Fig.12 Phase trajectory of the steady state solution of the cubic stiffness system and the segmented linear system

为获得更大的声源级,可以通过增大电压的方式增加系统驱动力,以使系统能够获得更大的体积振速。而由于非线性刚度的引入,使得电压的改变对系统的刚度有所影响。通过改变参数电压U的大小,研究不同输入电压下线性系统与高静低动系统的声源级变化。如图13(a)所示,对于线性系统,当输入电压U增大时,线性系统的两个共振频率点位置不发生变化,幅值随之增大。如图13(b)所示,对于三次刚度系统,当输入电压U增大时,其谐振点位置向频率增大的方向移动。如图13(c)所示,对于分段线性系统,当输入电压U增大时,会伴随着非线性的产生,其谐振点位置也会向频率增大的方向移动。产生这种现象的原因在于,当电压输入较大,振动幅值超出分段线性系统预设的低动刚度区间后,会导致系统刚度突变至另一刚度。因此在实际使用时应当避免电压过大,使系统工作在预设低动刚度区间内,保持良好的线性特征。

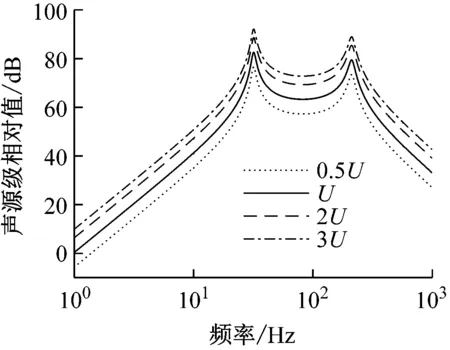
(a) 线性系统不同输入电压下的声源级

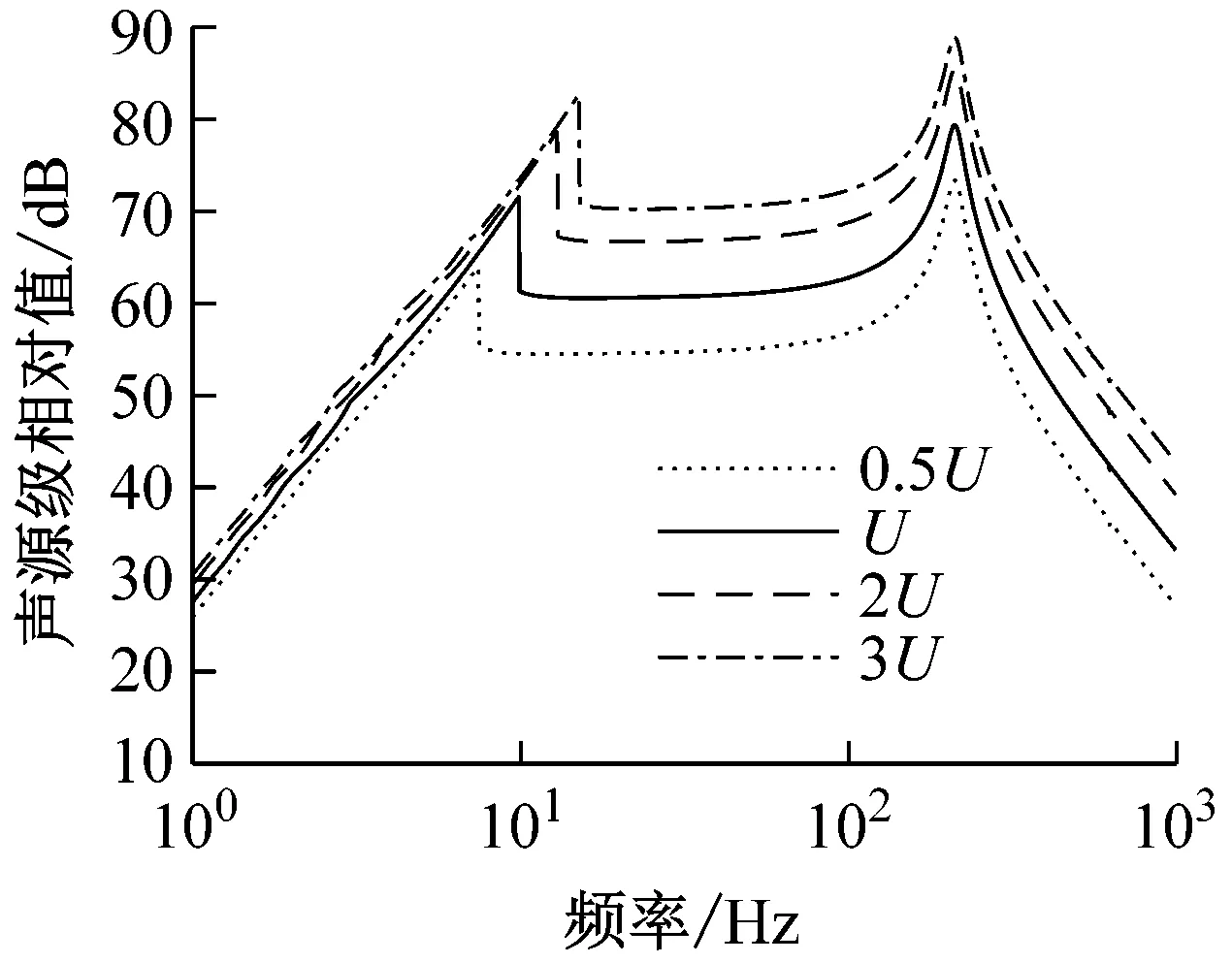
(b) 三次刚度系统不同输入电压下的声源级

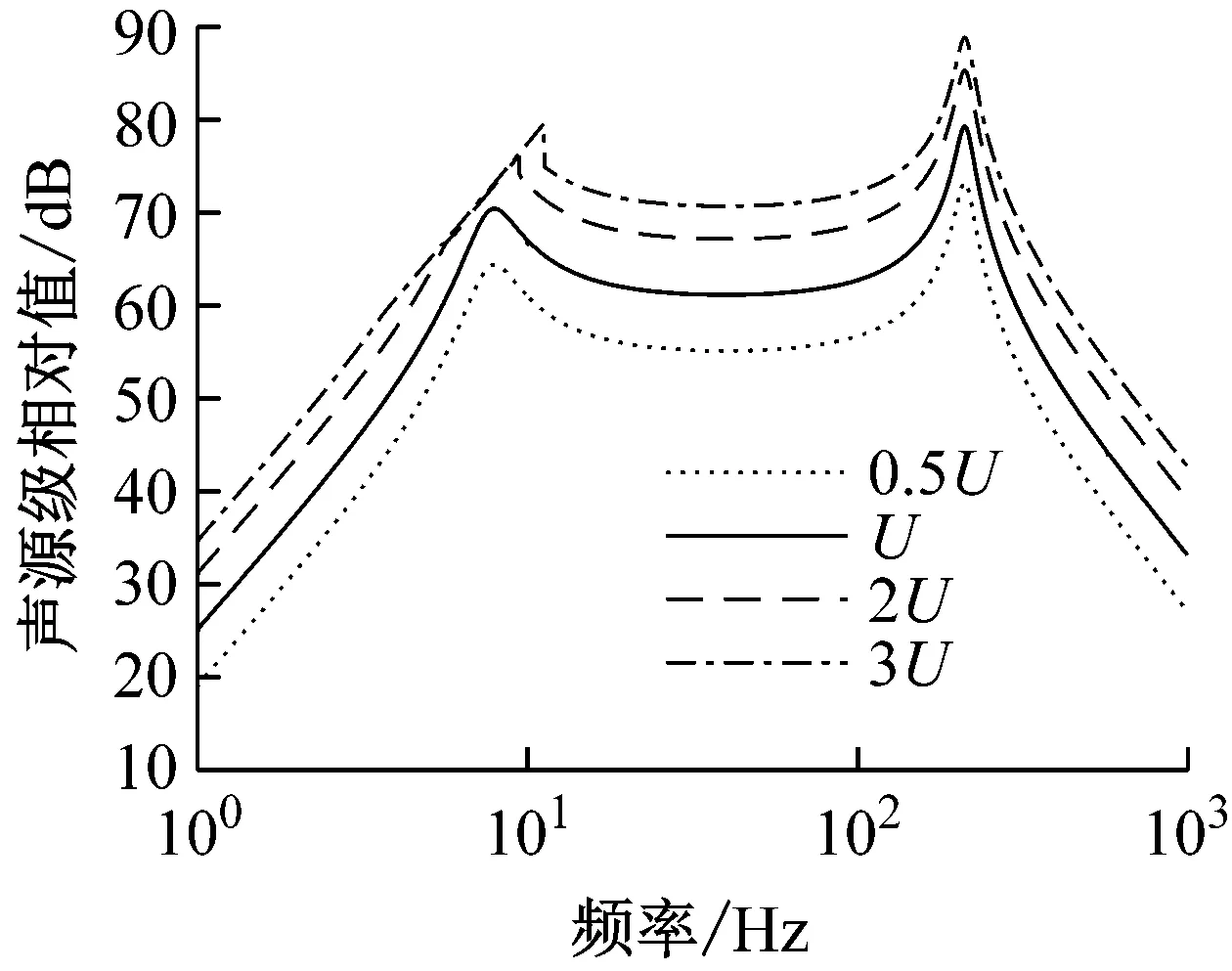
(c) 分段线性系统不同输入电压下的声源级图13 不同输入电压下的声源级Fig.13 SL response under different excitation voltage

三次刚度系统和分段线性系统均属于高静低动系统,两者具有不同的特点。一方面,当追求极低频率内的输出性能时,可以考虑三次刚度系统,这对于特定应用中的工作是有益的,但三次刚度系统在低动刚度工作区间内具有弱非线性。另一方面,当追求系统更大的低动刚度区间和良好的线性特征时,可以采用分段线性系统。分段线性系统的低动刚度区间可以设置得比三次刚度系统大,这有利于系统在大振幅时保持良好的线性特征,但当系统振幅过大超出低动刚度区间时,由于力-位移曲线切线斜率变化,系统刚度突变,导致其非线性特征反而会突出,这对正在工作的系统会产生不利的影响。

因此,在选择系统刚度的时候,需要根据具体的需求和应用背景来综合考虑,权衡三次刚度系统和分段线性系统的特点,以达到最佳的工作效果和性能。

在实际安装应用时,电磁换能器的驱动线圈与辐射板粘接,若粘接可靠,可将线圈与辐射板视为一体,此时换能器的机械部分系统可进一步简化。在对简化系统进行数值仿真分析时,将线性系统及高静低动系统模型中线圈与辐射板之间的刚度和阻尼参数给到足够大,可以得到图14所示的线性系统、三次刚度系统与分段线性系统的声源级。

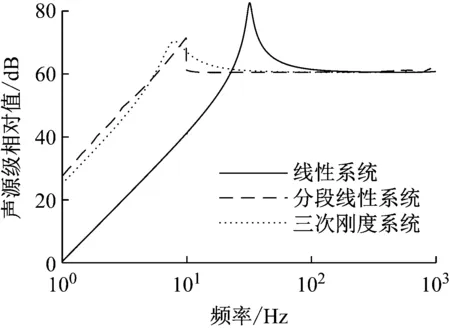
图14 不同简化系统的声源级Fig.14 SL for different simplified systems

3 锤击法测量固有频率

为了验证引入高静低动型悬架后,换能器的谐振频率降低,且在工作时具有更好的输出性能,对高静低动型悬架(“凸轮-弹簧-滚子”装置)和对应的线性悬架(线性弹簧)分别用锤击法测量悬架的固有频率,以进行原理性试验验证。试验装置如图15所示。各构件的参数列于表2中。其中运动部件质量指凸轮组件、弹簧及砝码平台上的总质量,凸轮轮廓曲线采用分段线性形式设计。当承受恒定压力Fc=96 N,线性悬架静变形量为y0=0.045 m,高静低动悬架在达到平衡位置后,整体的回复力与振动位移的函数表达式如式(24)所示,其中α=1/3。

表2 试验系统参数Tab.2 Test system parameters

(a) 高静低动型悬架试验图

(b) 线性悬架试验图图15 不同悬架装置试验图Fig.15 Test diagram of different suspension devices

(24)

试验平台主要有“凸轮-弹簧-滚子”装置、力锤、砝码、HD-YD-213加速度传感器、LMS SCADAS XS 数据采集仪和笔记本电脑等。悬架装置为测试对象,力锤用于对测试对象施加宽频成分的冲击载荷,砝码作为恒定负载施加于被测对象,加速度传感器安装于负载平台上用于测量台面振动加速度,LMS数据采集分析仪采集并处理力锤输入的力信号与加速度传感器获得的响应信号,笔记本电脑用于观测、记录数据并对其进行后续处理。试验所采用的衡量指标为加速度导纳,加速度导纳可以反映系统的固有振动特性,不会受到测试中施加的激励大小的影响,且由式(21)和式(22)可知,加速度的大小与声源级正相关。

试验中,先对高静低动型悬架进行锤击试验,完成试验后将“凸轮-弹簧-滚子”装置中的横置滚子机构移除并更换竖置弹簧,得到与高静低动型悬架对应的线性悬架。试验时,加速度传感器安装位置保持一致。

试验可测得所有频率范围内的加速度导纳,为方便展示对比效果,频率范围设置为0～10 Hz。在仿真计算中,将阻尼统一设为14.5 N·s/m,以使线性悬架仿真结果与试验结果具有相同的峰值,悬架装置试验结果和参数仿真结果如图16所示。线性悬架试验得到的固有频率为2.38 Hz,与仿真值2.40 Hz相近,高静低动型悬架试验所得固有频率为1.5 Hz,与仿真结果1.21 Hz存在差异,且试验得到的峰值2.73 m/(N·s2)与仿真峰值5.18 m/(N·s2)相差较大,原因可能为试验结果受试验装置加工装配误差、滚子半径误差以及凸轮和滚子之间摩擦力的影响。由试验结果可知,相较于线性悬架,在承载相同负载时,高静低动型悬架的固有频率下降约36.98%,且在相同激励下低频时加速度更高。将高静低动型悬架应用在电磁换能器中,可降低换能器的谐振频率,提升低频段内的声源级。

4 结 论

(1) 基于高静低动刚度特性原理,设计了一种用于电磁换能器的凸轮-弹簧-滚子装置,推导了引入高静低动刚度前后换能器的系统模型。

(2) 建立了此凸轮-弹簧-滚子装置理想力-位移曲线与凸轮实际轮廓曲线之间的映射关系。其力-位移曲线不受结构特征的限制,对于给定的力-位移方程均可设计得到与之对应的凸轮轮廓曲线。

(3) 借助推导的换能器系统离散模型,对引入高静低动刚度前后的换能器声源级进行了数值仿真分析对比,探究了输入电压的变化对不同系统的影响。分析得到,引入高静低动刚度后,换能器的谐振频率降低,振速、声源级均高于原线性系统;输入电压的变化会改变高静低动系统的谐振频率和刚度特性。对于不同的高静低动系统,三次刚度系统在极低频率内的声源级优于分段线性系统,而分段线性系统在低动刚度工作区间内可以保持良好的线性特征。

(4) 通过锤击法测量“凸轮-弹簧-滚子”装置的固有频率,与原线性系统的悬架固有频率比较。试验得到,在承载相同负载时,高静低动型的固有频率相较于线性悬架下降约36.98%。

本文提出的基于高静低动原理的悬架装置为电磁换能器在低频宽带方面的研究提供了一种新的思路,具有一定的应用前景。