二十辊轧机辊系耦合振动特性及振动控制

孔祥岚, 和东平, 徐慧东, 王 涛, 黄庆学

(1.太原理工大学 机械与运载工程学院,太原 030024;2.先进金属复合材料成形技术与装备教育部工程研究中心,太原 030024)

轧机振动在带钢轧制过程中普遍存在,严重的振动不但对带钢质量产生不利影响,而且会严重影响设备健康运行。在极薄带轧制过程中影响更为显著[1]。Kapil等[2]基于四辊轧机建立了非线性参激系统,利用多尺度法分析了系统稳定性与幅频特性。Zhang等[3]建立了轧机非线性水平-垂直-扭转耦合模型,分析了不同外激励幅值下工作辊的幅频特性以及不同辊缝下的工作辊动态分岔特性。刘飞等[4-6]以四辊轧机为例,探究了液压缸内分段弹性力和摩擦力约束对系统幅频特性的影响,同时对系统分岔特性和稳定性进行了分析。Zhang等[7]考虑油缸非线性摩擦,分析了PID控制下的轧机垂直振动特性。Hou等[8-9]基于轧制变形区油膜厚度的动态影响,建立了轧机纵横耦合非线性动力学模型,通过数值仿真分析了界面接触率非线性参数等因素对主共振幅频特性的影响。Peng等[10-11]考虑到轧件弹塑性变形,建立了四辊轧机滞后非线性垂直振动模型,采用多尺度法分析了线性刚度与非线性刚度对1/2亚谐波和1∶1内共振幅频特性的影响。通过时滞位移控制,分析了增益系数与延迟时间对振幅以及共振区域的影响。Lu等[12]利用Hopf分岔定理和Routh-Hurwitz行列式,分析了多自由度耦合轧机振动系统分岔特性,研究了不同轧制条件对系统稳定性的影响。

由于二十辊轧机结构复杂,辊系的分析在板形控制方面十分重要,包括参数计算[13],工艺优化[14],凸度调控[15],辊系变形分析[16]以及整体控制策略[17-18]等。然而对二十辊轧机辊系振动的研究并不多见。Wu等[19]基于二十辊轧机辊系结构,建立线性水平-垂直振动耦合动力学模型,仿真分析了不同轧制力与轧制速度对工作辊振动特性的影响。在此基础上,提出了工作辊表面出现缺陷下的时变刚度动力学模型,通过数值仿真[20],三维模型有限元模拟[21]和试验分析验证了动力学模型的有效性。Wang等[22]分析了静态与动态下辊系间接触力的变化。袁凯等[23]通过建立二十辊轧机有限元模型,分析了不同轧制力对于辊系稳定性的影响。

振动问题会给轧机带来许多负面影响,因此,抑制轧机振动已成为机械设计和振动控制领域共同关注的焦点。为了实现对轧机振动的有效控制,Qi等[24]分析了轧机模数控制增益对耦合振动的影响,并提出通过降低轧机模数控制AGC增益来缓解轧机振动。Qian等[25]提出一种自适应模糊轧机垂直振动控制方法,可以计算未知的非线性函数和系统参数,通过仿真证明了该系统的稳定性。华长春等[26]提出了一种自适应预定性能控制方法,用于非线性不确定的轧机振动模型,可以避免扭振现象的产生。Zeng等[27]通过设计线性与非线性反馈控制器实现了轧机垂直水平扭转耦合系统的Hopf分岔控制,并研究了线性增益系数与稳定性区域的关系以及非线性增益系数对振幅的影响。Wang等[28]利用非线性控制器有效控制了轧机主传动时滞系统的Hopf分岔,仿真结果表明振动幅值得到了有效的抑制。张义方等[29]提出通过电气改造来抑制电气驱动谐波,进而实现对轧辊扭振的控制。和东平等[30]设计了一款非线性参数分岔控制器,可以用于控制波纹辊轧制系统的跳变以及时滞现象。

Washout滤波控制器是一种可用于线性与非线性系统的状态反馈控制方法,具有改善系统性能,精准控制,降低误差,实时响应等特点,被广泛应用于机械、电气等领域。Zhai等[31]验证了Washout滤波控制器对非线性系统Hopf分岔的有效控制以及系统稳定性的提升。Liu等[32]将Washout滤波控制器用于轧机机电耦合扭转系统,研究了时间常数,线性增益对Hopf分岔点的影响以及非线性增益与振动幅值的关系。

本文在专家学者对轧机振动的研究基础上,根据极薄带轧制工艺与二十辊轧机辊系特点,提出了具有非线性轧制界面与耦合振动特性的简化动力学模型,并对其振动特性和振动控制展开研究。

1 二十辊轧机模型及其动力学方程

二十辊轧机因具有整体刚度大,板形控制能力强以及轧制极限厚度小等特点,主要用于轧制精密极薄带,如图1所示。图2为二十辊轧机辊系,由工作辊、第一中间辊、第二中间辊(图2中:b为惰性辊;a、c为驱动辊)以及背衬辊组成。

图1 二十辊轧制机组Fig.1 20-high rolling mill

1.工作辊;2.第一中间辊;3.第二中间辊;4.背衬辊。图2 二十辊轧机辊系结构图Fig.2 The roll system of 20-high rolling mill

在二十辊轧机工作过程中,工作辊振动决定极薄带产品质量,而与工作辊接触的第一中间辊会对工作辊的振动产生直接影响。故本文从二十辊中提取由工作辊和第一中间辊组成的六辊进行研究。由于辊系之间为圆柱辊身线接触,忽略其辊系间阻尼的作用。同时基于轧制工艺不同以及润滑状态的变化产生非线性因素,故考虑了工作辊与极薄带之间的非线性刚度以及非线性阻尼。基于上述简化情况,结合轧机上下对称结构,建立六自由度非线性动力学模型,如图3所示。

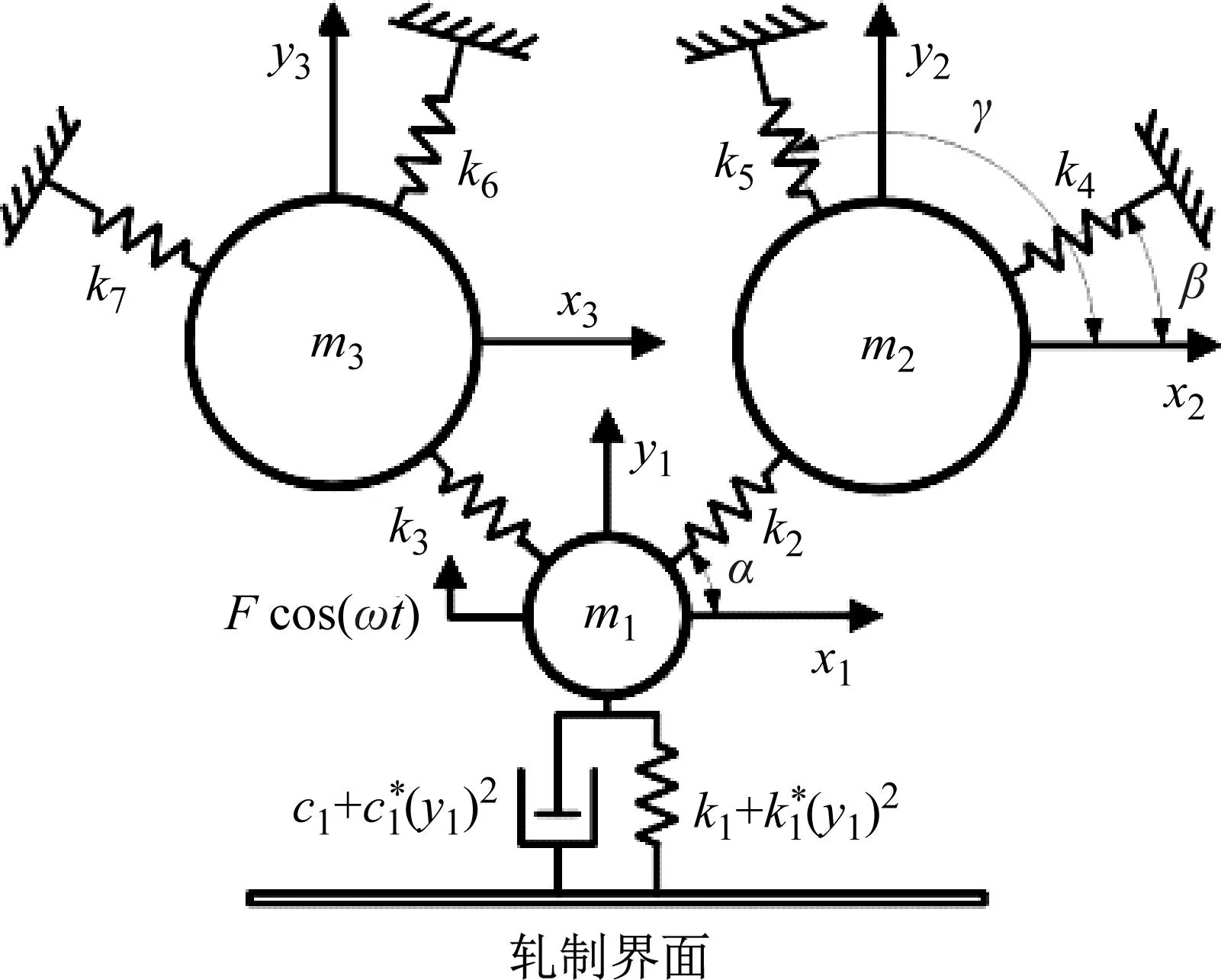
图3 二十辊轧机简化后六自由度动力学模型Fig.3 Six-degree-of-freedom dynamic model of 20-high rolling mill after simplification

图3中,简化后六自由度动力学模型参数如表1所示。建立系统动力学方程如下

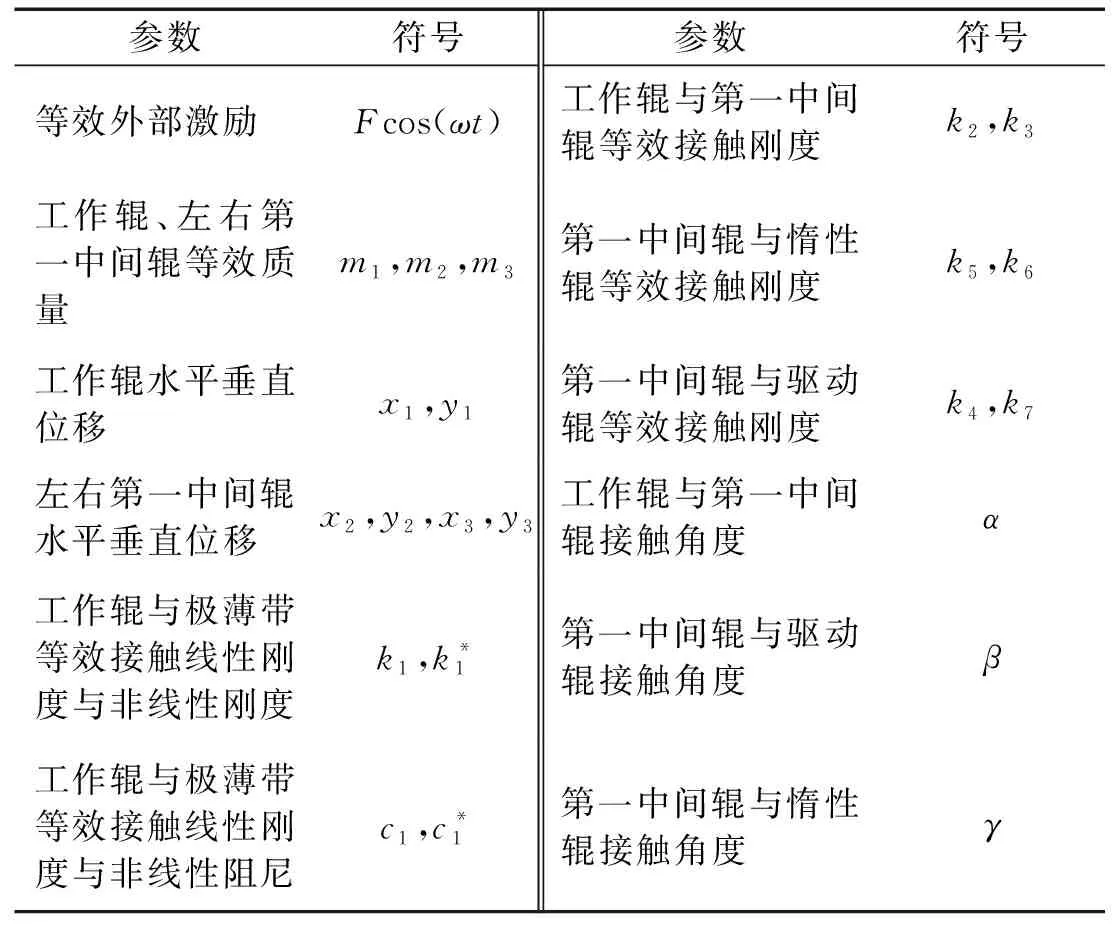
表1 六自由度动力学模型参数Tab.1 Parameters of six-degree-of-freedom dynamic model

(1)

由结构的左右对称性以及m1的水平初始位移为零,式(1)可简化为

(2)

2 轧机辊系主共振特性分析

2.1 主共振响应求解

对于非线性方程,很难进行精确值求解。通常采用近似值求解,在一定精度下,近似值可以替代精确解进行研究。本文采用多尺度法进行方程求解[33],引入下面的无量纲量,将方程(2)转化成如式(3)所示的无量纲形式

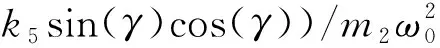
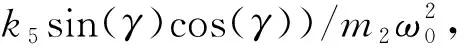
(3)

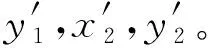
(4)

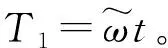
(5)

(6)

(7)

设零阶近似方程组(6)的解为

(8)

将式(8)代入式(7)得

k1-2A2eiω20T0-c1-1iω10B1eiω10T0-

2D1iω10B1eiω10T0+cc

2D1iω20A2eiω20T0+cc

2D1iω30B2eiω30T0+cc

(9)

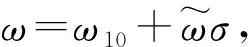
(10)

为了方便式(10)求解,将B1,A2,B2设定为指数形式

B1=0.5b1eiφ1,A2=0.5a2eiφ2,B2=0.5b2eiφ3

(11)

式中,b1,a2,b2,φ1,φ2,φ3为时间T1的函数。

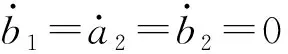
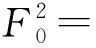
(12)

2.2 主共振特性分析

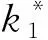
(a)

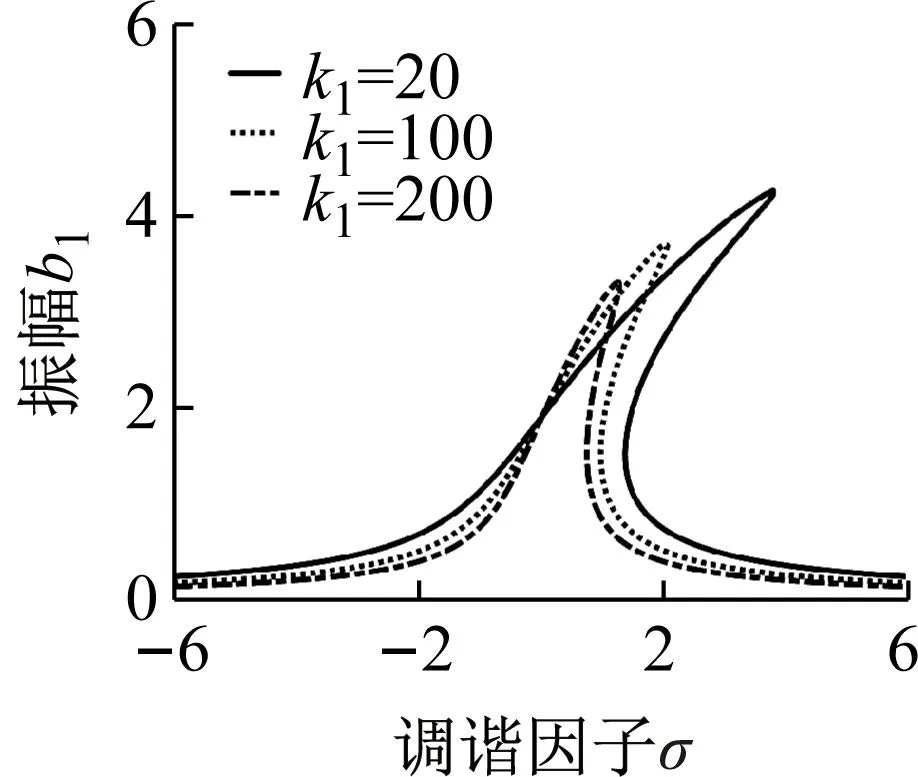
(b)

(c)

(d)

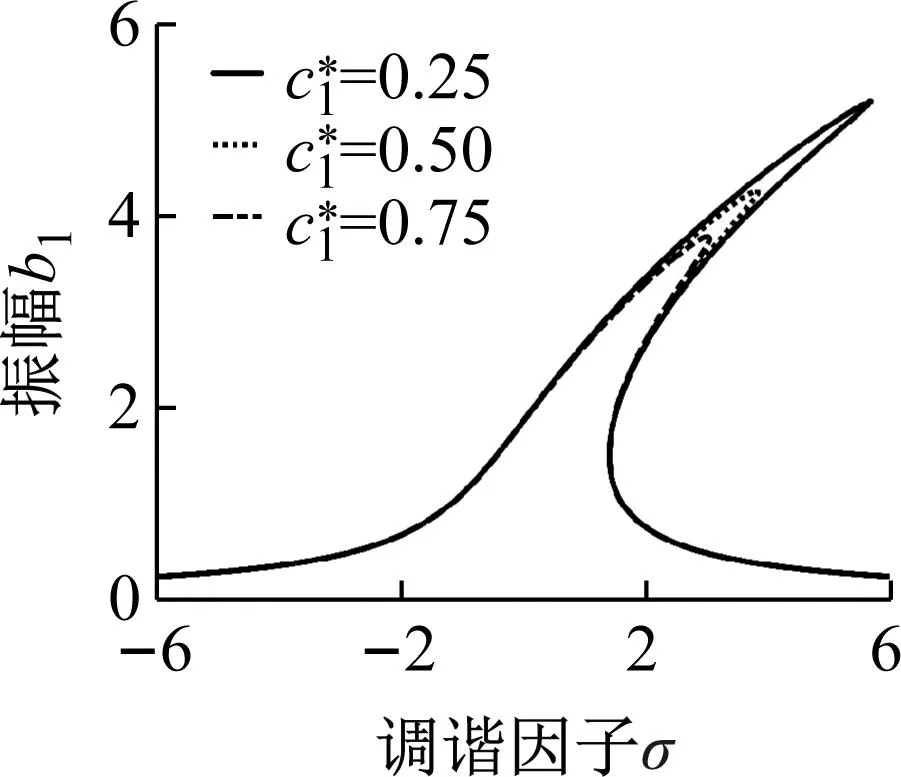
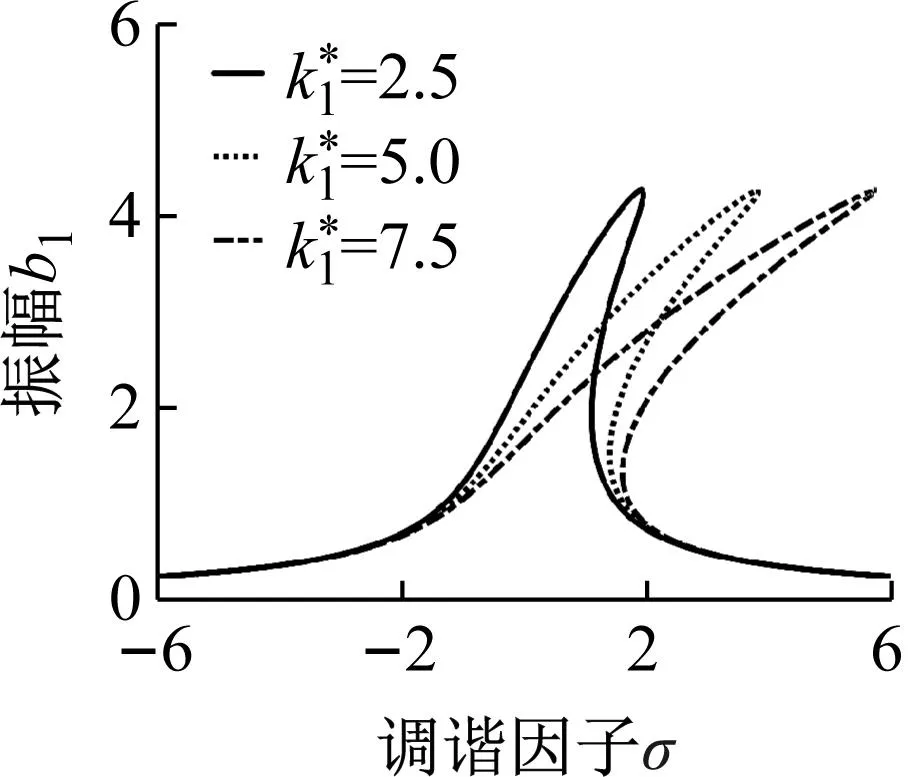
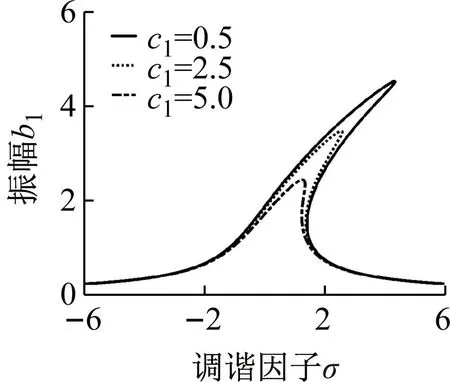
(e)图4 不同参数对主共振幅频特性曲线的影响Fig.4 Primary resonance amplitude frequency curve with the influence of different parameters

在轧制生产过程中,通过调整轧制速度,减小材料张力的波动以及选取合适的润滑剂,使工作辊受到外部扰动力得以抑制,同时轧制界面上刚度阻尼得到相应的改变,进而实现共振区域的减小和振峰弯曲程度的弱化,减小主共振对于极薄带轧制生产的影响。

3 轧机辊系内共振特性分析

3.1 共振响应求解

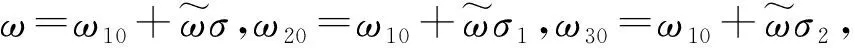
(13)

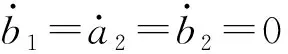
2k1-2a2(b2k1-1sin(θ3)-

(14)

式(14)中一些量的详细表达式见附录A。

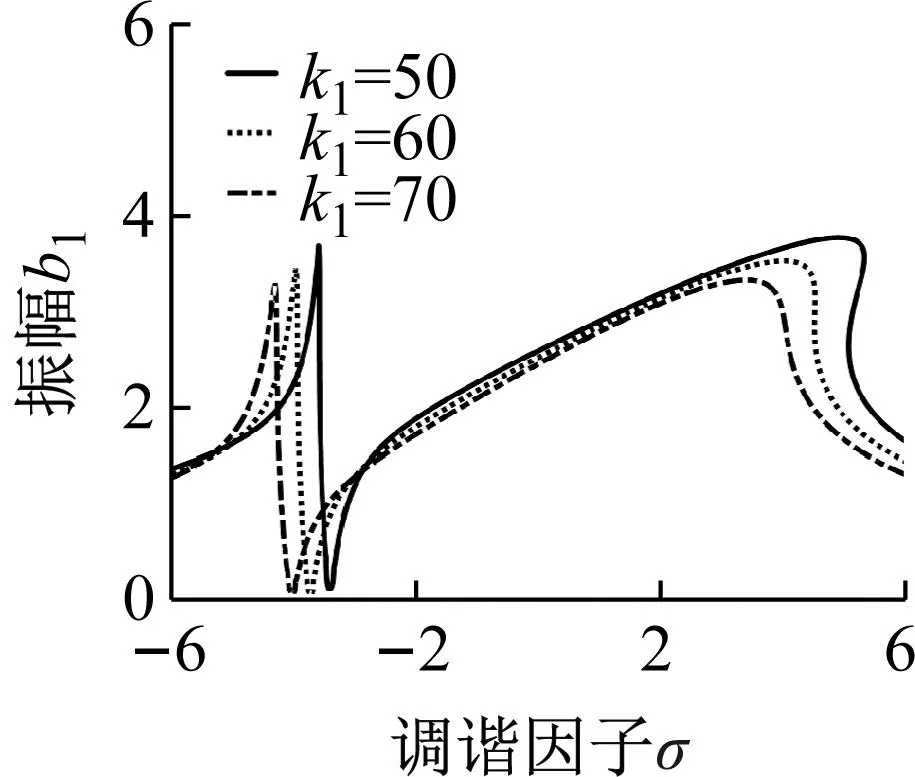
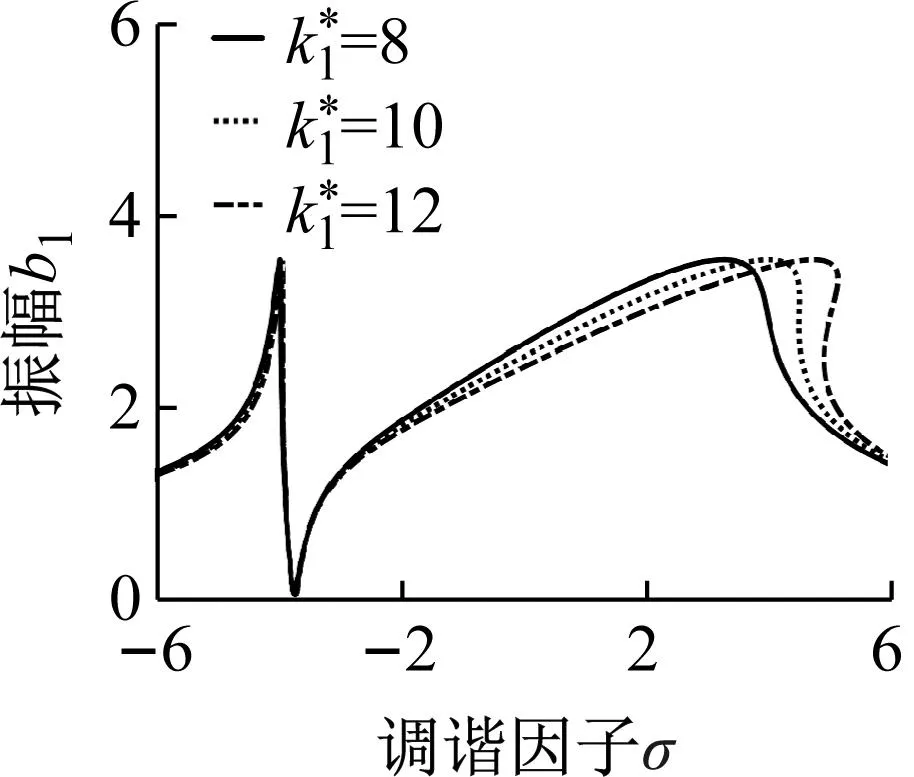
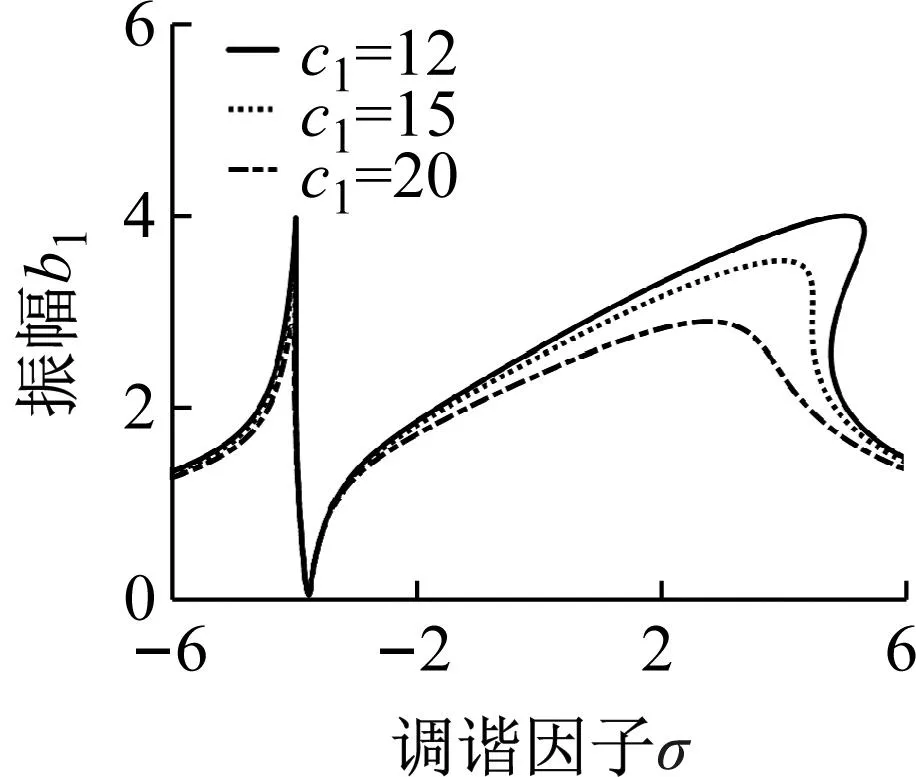
3.2 内共振幅频特性分析

(a)

(b)

(c)

(d)

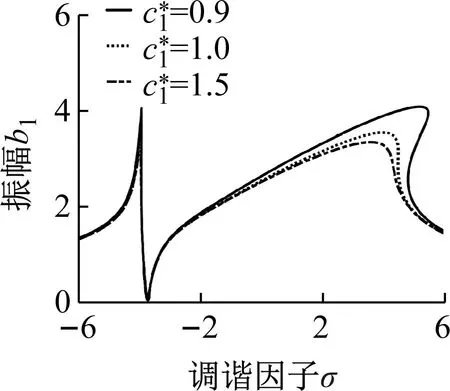
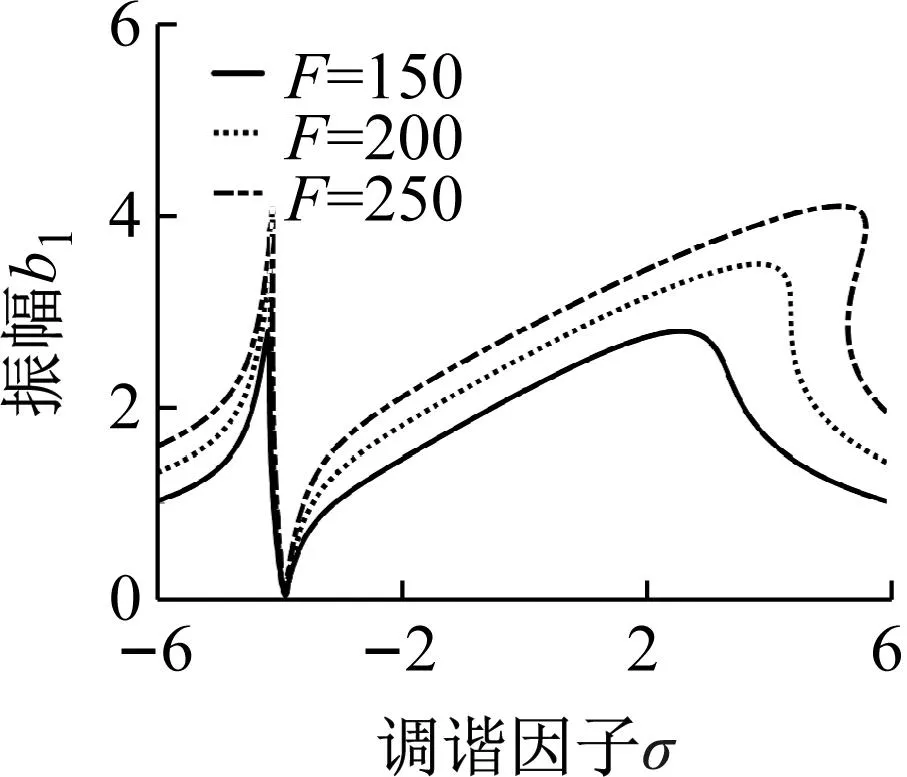
(e)图5 不同参数对内共振幅频特性曲线的影响Fig.5 Internal resonance amplitude frequency curve with the influence of different parameters

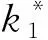
4 谐波振动的稳定性分析

通过对幅频特性曲线观察发现,该系统因存在非线性而产生跳跃现象。本章对系统稳定性以及全局性态进行分析来揭示这种跳跃现象。

根据式(12)和式(14),可以归纳化简为以下形式

(15)

这里,对于主共振情形,式(15)中Φ和Ψ如下

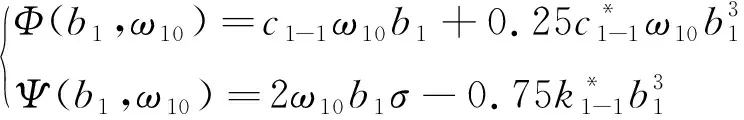
对于内共振情形,式(15)中Φ和Ψ如下

将式(15)两个方程相除,化为自治形式一阶微分方程

(16)

当外部扰动力幅值F0和频率ω10给定后,通过一阶微分方程式(16)可确定动相平面内的相轨迹。其中动相平面内的奇点(bs,θs)则对应系统的平衡态。奇点(bs,θs)满足以下方程

(17)

从式(17)消除θs得到幅频特性方程

(18)

引入扰动变量ξ=b1-bs和η=θ1-θs,并根据式(15)在奇点(bs,θs)附近取一次近似式

(19)

扰动变量一阶微分方程式(19)本征方程为

(20)

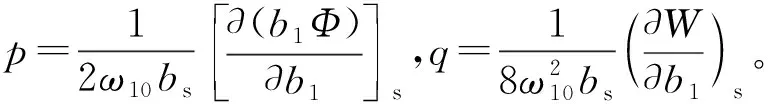
根据李雅普诺夫的一次近似稳定性判据[35],根据实际参数计算给出解bs,θs渐进稳定的充分条件为q>0,根据该条件在主共振和内共振幅频曲线图中绘制稳定区域和不稳定区域判别曲线。此判别曲线将幅频曲线分为稳定解曲线和不稳定解曲线(虚线)两部分,如图6(a)和图7(a)所示。

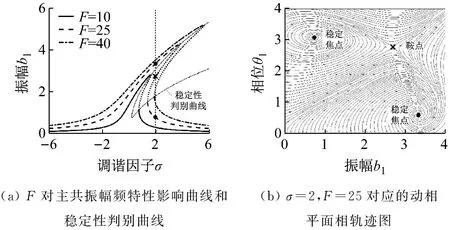
图6 主共振稳定性判别及相轨迹分析Fig.6 Primary resonance stability discrimination and phase trajectory analysis

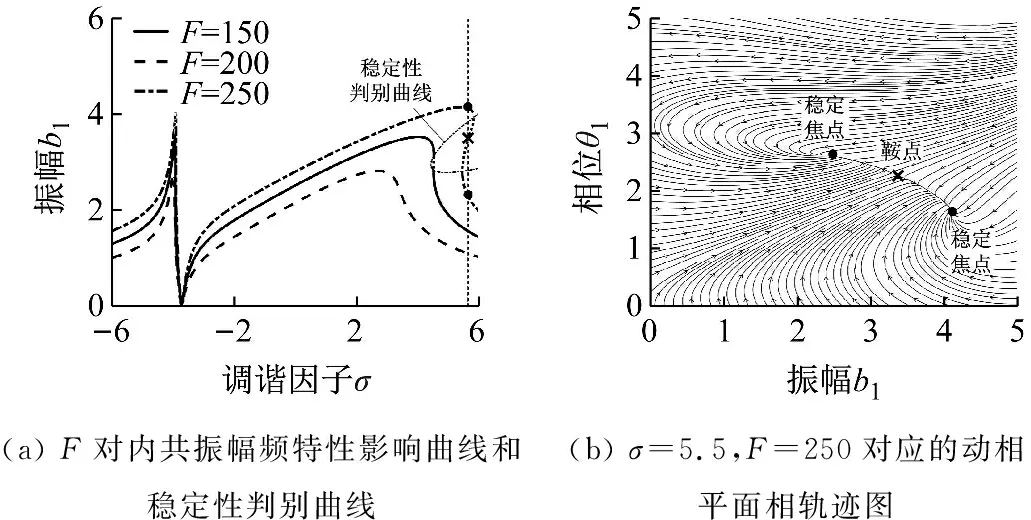
图7 内共振稳定性判别及相轨迹分析Fig.7 Internal resonance stability discrimination and phase trajectory analysis

以图6和图7所示的主共振和内共振情形为例来分析谐波振动的稳定性,在图6(a)和图7(a)中分别取σ=2,F=25及σ=5.5,F=250进行分析,并绘制相应的相轨迹图,如图6(b)和图7(b)所示。结合幅频曲线图与相轨迹图分析,可以看出当外部扰动频率固定时,与振峰稳定解曲线相交的两个点属于稳定焦点,而与振峰腰部相交的不稳定解则以鞍点的形式出现。从相平面相轨迹图可以看出,主共振情形的稳定焦点和内共振情形的稳定结点均与不稳定鞍点共存,过鞍点的分隔线划分出稳定焦点和稳定结点的不同吸引盆,这正是引起幅频特性曲线出现跳跃现象的原因。

5 轧机辊系的静态分岔分析

在第2章得到的主共振幅频方程(12),获得b1的分岔方程,将其简化为以下形式

(21)

式(21)可写为

(22)

式中:m,n为开折参数;μ为分岔参数。m,n,μ见附录B。令:

(23)

根据奇异性理论[36],式(23)是GS范式g(y,μ)=y7-μy=0的普适开折,奇异点为余维二的叉形点,于是系统有如下的分岔点集:

(1) 分岔点集B=φ

(4) 系统转迁集∑=B∪H0∪H1∪D

根据分岔点集(4)得到转迁集如图8所示,图中曲线将平面分为四个区域(Ⅰ,Ⅱ,Ⅲ,Ⅳ),不同区域以及临界点所对应的拓扑结构如图9所示。

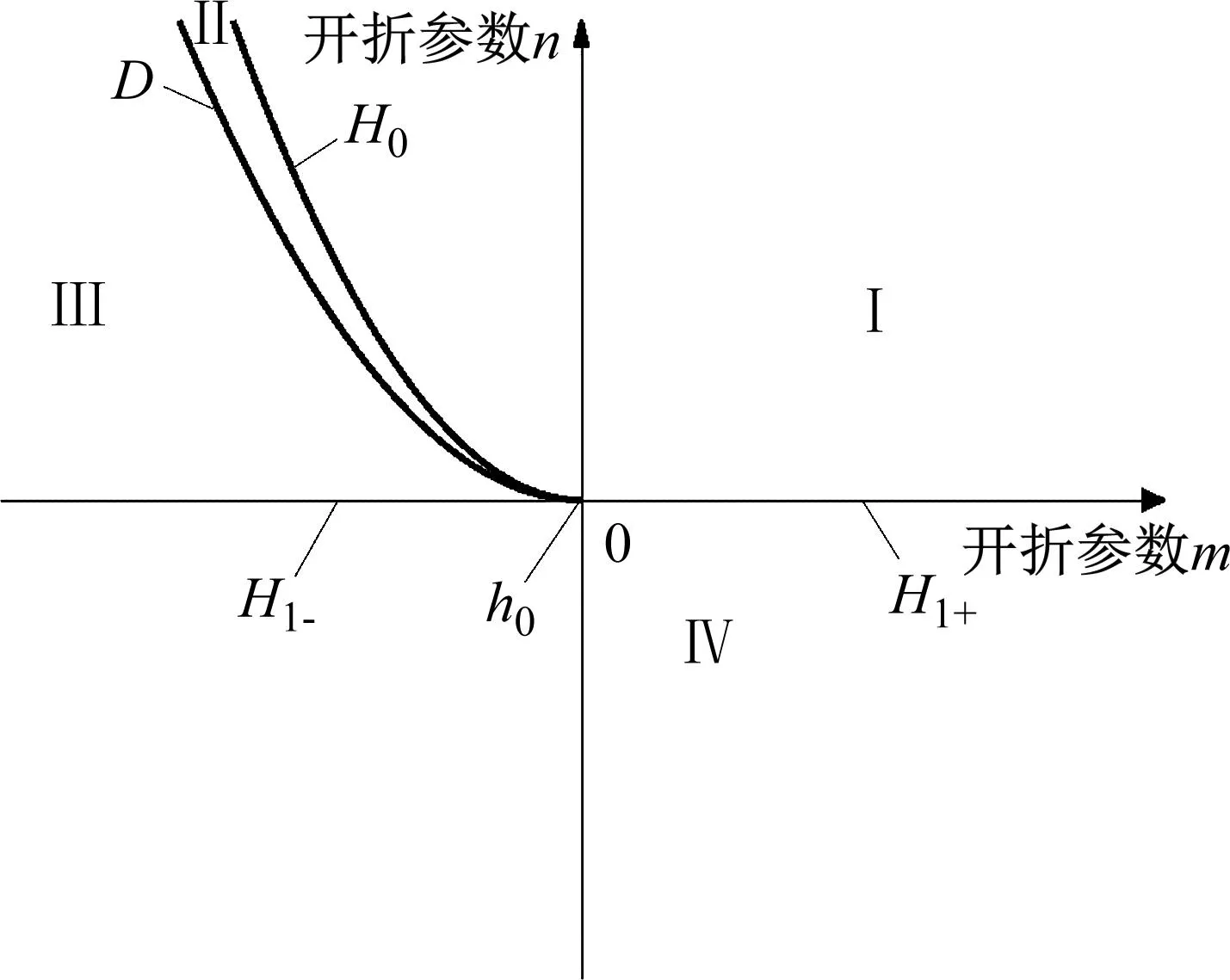
图8 系统转迁集Fig.8 System transition set

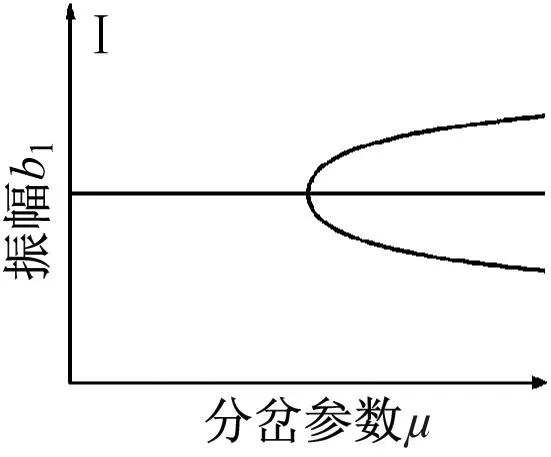
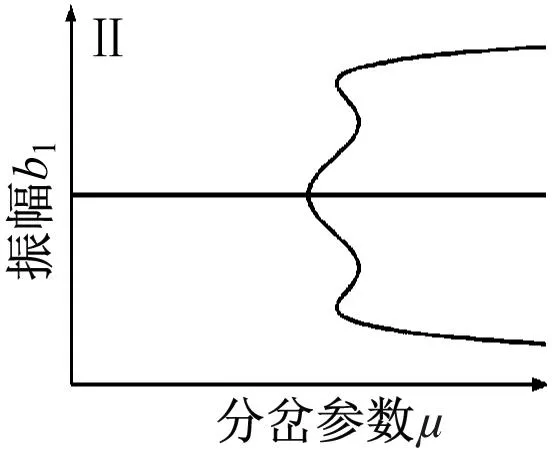
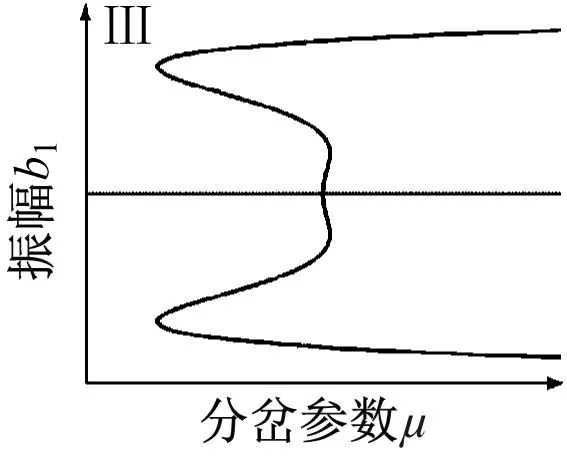
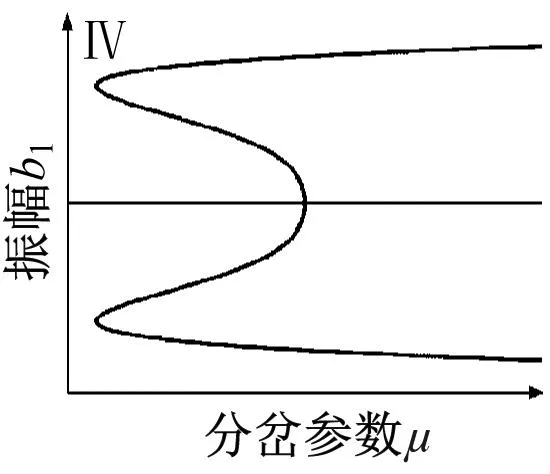
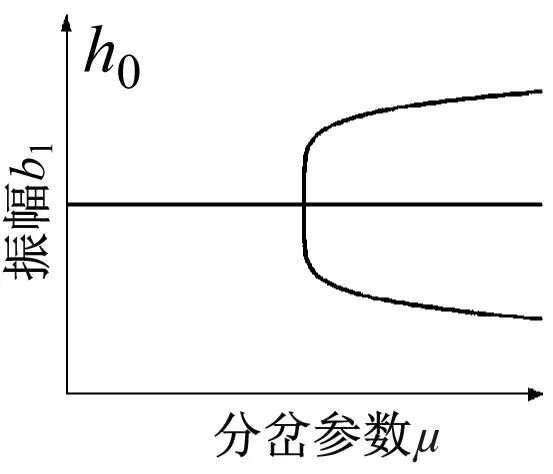
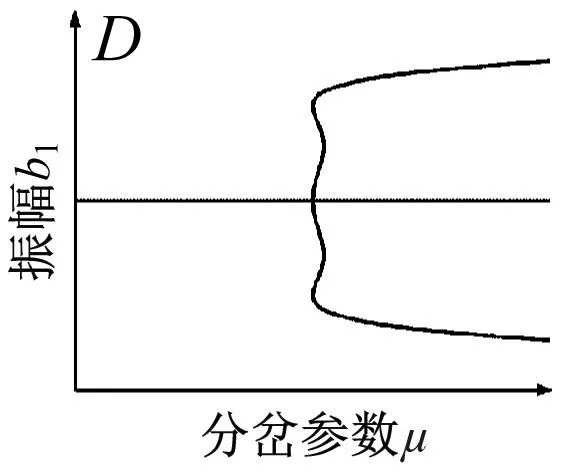
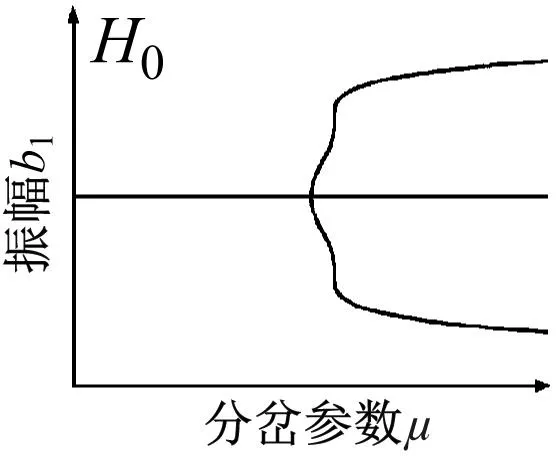
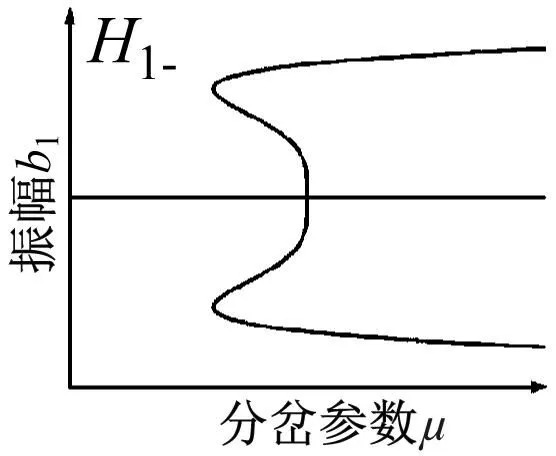
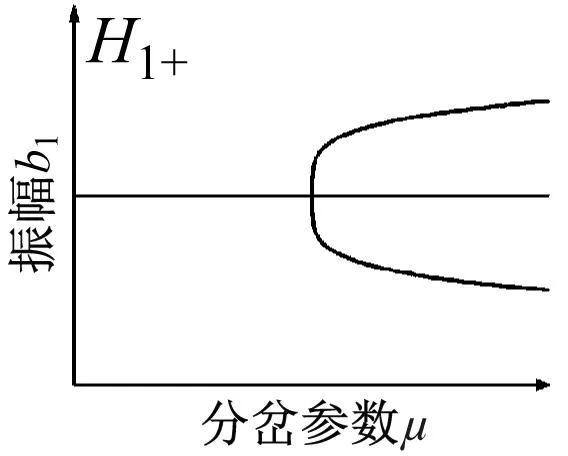
图9 系统拓扑结构图Fig.9 System topology diagram

图9中的局部分岔行为反映了系统的所有静态分岔信息。当开折参数落在临界曲线D时,随着μ值增大,存在b1多解且跃迁现象,这将会导致系统振动显著。当开折参数落在临界曲线H1-,H1+以及H0,系统出现滞后现象。当开折参数穿过滞后点集进入区域Ⅱ,在分岔参数μ增大过程中,系统出现跳跃现象。当开折参数穿过双极限点集进入区域Ⅲ,Ⅳ观察到明显的两个极限点,可使系统在μ值较小时便产生明显振动。当开折参数处于区域Ⅰ,系统拥有较大稳定区域,且不存在滞后跳跃等现象,可以有效降低系统振动。因此,在工程实践中,有必要控制轧机的各种参数,以使开折参数m和n在区域Ⅰ中,从而提高极薄带轧制过程的稳定性。

6 轧机辊系的振动控制

为了提高轧机系统稳定性,使工作辊振幅得到有效控制,设计一种状态反馈控制器来降低扰动对系统稳定性以及工作辊振动的影响。

6.1 状态空间表达式变换

状态空间表达式变换方法是用来简化非线性方程计算的可行数学方法,可以将系统平衡点转移至原点,得到等效模型。

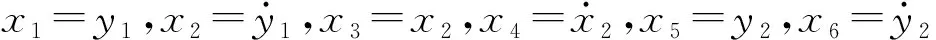
(24)

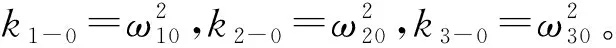
(25)

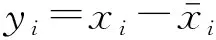
(26)

6.2 控制器设计

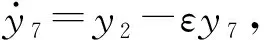
(27)

系统(27)的线性化矩阵为

线性化矩阵B的特征方程如下

λ7+p1λ6+p2λ5+p3λ4+p4λ3+

p5λ2+p6λ+p7=0

(28)

特征方程(28)的系数见附录C。

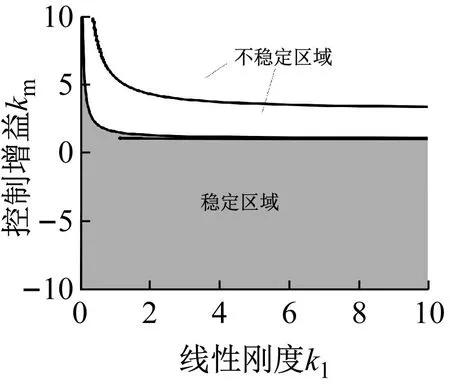
特征方程式(28)的根均含有负实部是判断系统稳定的充要条件,根据Routh-Hurwitz判据条件[38]得到如图10所示的系统的稳定性控制区域,当ε=0.1,在正刚度与正阻尼作用下,控制增益km<0即可满足系统稳定性条件。此时加入控制器的系统的平衡态是渐近稳定的,这表明通过合理地选取控制器的控制增益,可提高系统的稳定性。

(a)

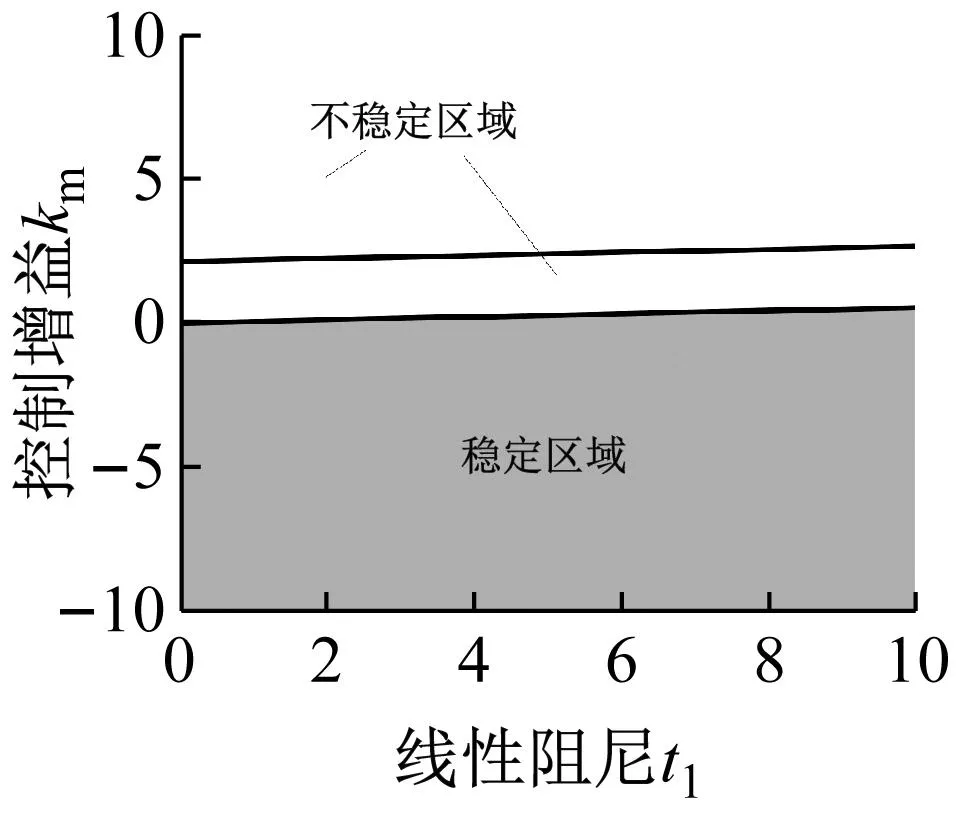
(b)图10 不同系统参数与控制增益系数确定的稳定区域Fig.10 The stability region determined by different system parameters and the optimal control gain

6.3 受控系统幅频特性

将受控系统(27)转化为如下形式

(29)

(30)

其中:

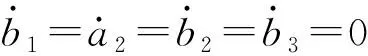
(31)

根据幅频方程(31)可绘制幅频曲线如图11所示。可以看出,随着控制增益km的减小,共振峰值得到明显降低,但km达到一定程度后继续减小,峰值不会降低,相邻频率下的振幅增大,但振峰弯曲程度减弱,跃迁不稳定性逐渐减弱。由此可知,增益系数选取适当值,可以实现在不增大相邻频率幅值的情况下,降低工作辊振幅且使系统稳定性得到提升。

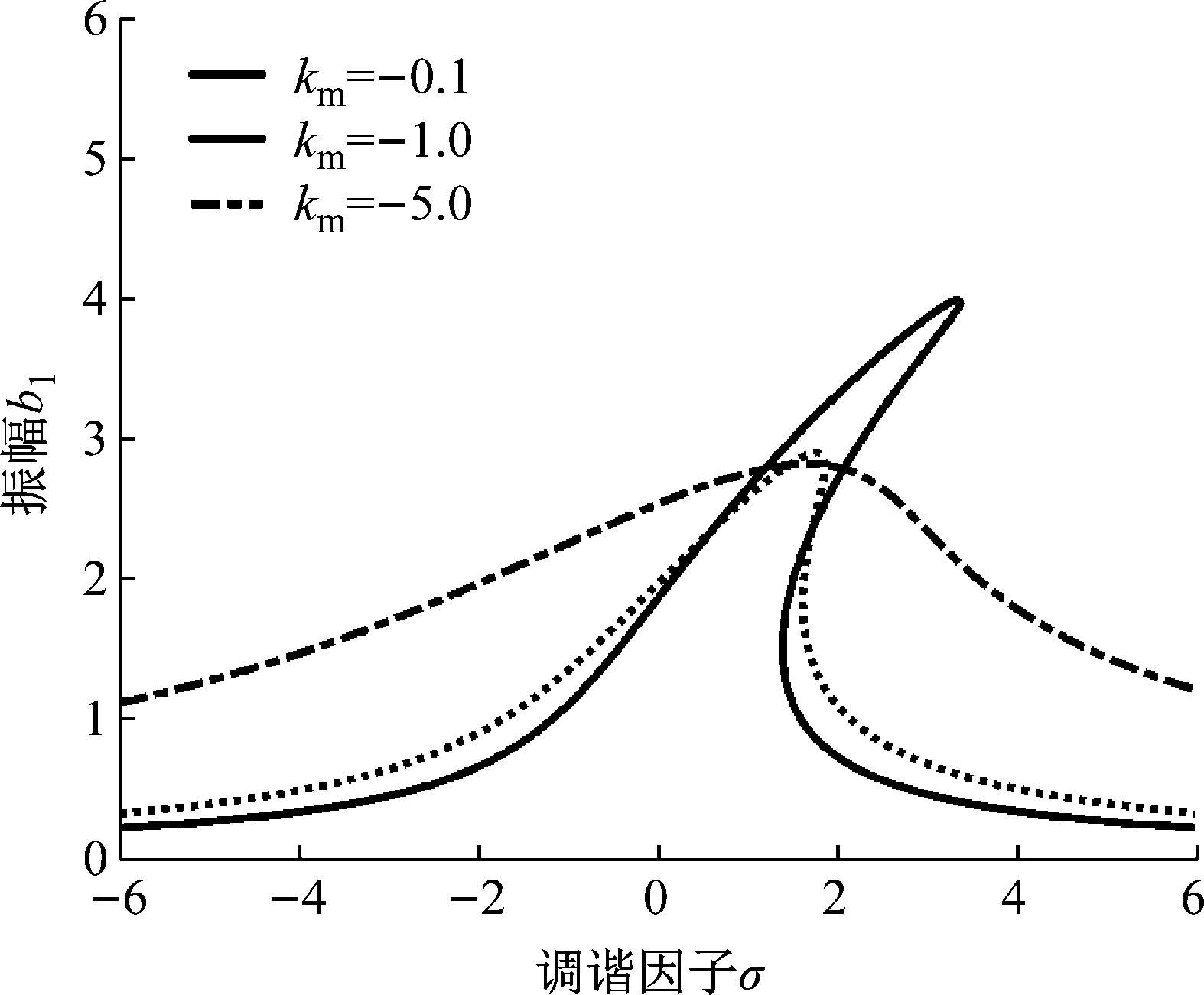
图11 控制增益对系统幅频特性曲线的影响Fig.11 Amplitude frequency curve with the influence of the optimal control gain

6.4 数值仿真

综合某实验室280 mm森吉米尔二十辊轧机设备参数,取实际参数如表2所示。

表2 280 mm森吉米尔二十辊轧机设备参数Tab.2 Equipment parameters of 280mm Sendzimir 20-high rolling mill

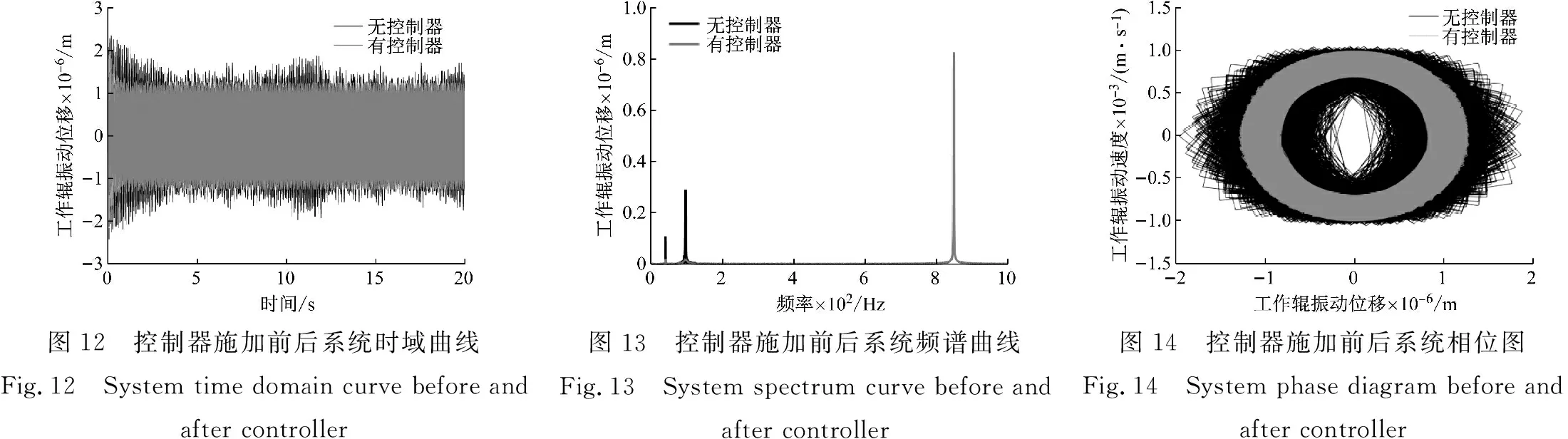
由于工作辊在轧制过程中还会受到板材张力波动,轧制速度变化等因素引起的轧制力波动[39-40],故归结设定为外部扰动力F=13 kN。为了验证所设计的控制器的抑振效果,结合上述参数,调整控制增益km=-100,通过数值仿真,得到控制器施加前后时域曲线,相位图,频谱曲线和Poincaré截面图如图12～图15所示。

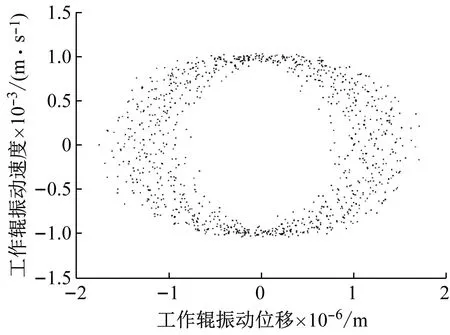
(a) 未施加控制器系统

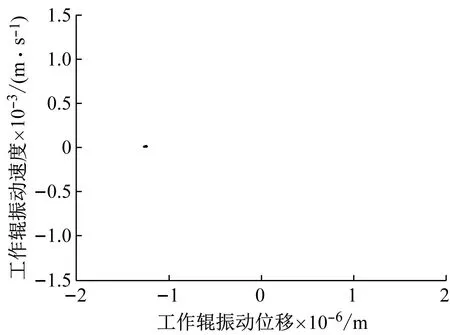
(b) 施加控制器后系统图15 施加控制器系统前、后的Poincaré截面图Fig.15 System Poincaré cross-section diagram before and after controller

从图12中可以看出,在原系统不稳定的运行状态下,施加控制器后系统在2 s左右达到稳定。原振动稳态最大位移幅值从2.0×10-6m稳定到1.5×10-6m,控制器可使系统振动得到一定程度抑制且系统稳定性得到明显提高。图13为频谱曲线,可以发现原系统振动包含三个共振频率,主共振频率在850 Hz附近,次谐波共振频率为50 Hz和100 Hz左右。施加控制器后,虽然主共振峰值没有发生明显改变。但次谐波共振峰值得到明显有效抑制。因此,控制器可以抑制工作辊的垂直振动,提高轧机稳定运行和产品质量。

图14表现为工作辊振动位移和振动速度的关系,可以看出施加控制器后,不仅使原系统的不稳定状态得以稳定,而且建立的新稳定周期振动的幅值减少幅度明显。图15是Poincaré截面图,对比图15(a)、(b)可以看出施加控制器前后,系统从杂乱的散点趋于稳定的一点,说明通过控制器作用,系统振动状态从不稳定状态控制进入稳定状态,进一步验证了所设计控制器对工作辊抑振的有效性,在提高系统稳定性方面具有良好的控制效果。

7 结 论

本文建立了一种简化二十辊轧机辊系的耦合振动模型,分析了辊系主共振和内共振情况下的振动特性及其稳定性,设计了一种状态反馈控制器对工作辊的振动进行了有效的控制,结论如下:

(1) 根据二十辊轧机辊系的结构特点及极薄带轧制工艺,简化提出了一种具有非线性的六自由度辊系水平-垂直耦合动力学模型,为进一步揭示轧机的振动特性及稳定性分析奠定了基础模型。

(2) 采用多尺度法求解得到了系统主共振和内共振两种振动情况下的幅频响应方程,分析了不同参数对各种共振情形下振动特性的影响。通过改变系统参数,可以有效减少共振区域,弱化跳跃现象,进而实现系统振动抑制。

(3) 根据李雅普诺夫一次近似稳定性判据,揭示了系统稳定焦点、稳定结点和不稳定鞍点的共存现象以及过鞍点的分隔线划分出的不同稳定奇点的吸引盆。基于奇异性理论分析了轧机共振稳态响应分岔方程的稳定性,给出了系统的转迁集和分岔拓扑结构图,表明控制开折参数落入区域Ⅰ中有助于提高系统的稳定性。

(4) 通过对系统进行状态空间表达式变换处理,基于Washout filter控制器原理设计了一种状态反馈控制器,通过分析控制增益对幅频特性的影响,表明选取适当控制增益可以实现在不增大相邻频率幅值的情况下,可降低工作辊振幅且提升了系统的稳定性;通过对比分析控制前后的时域图、相位图、频谱图以及Poincaré截面图,表明所设计的控制器具有良好的工作辊减振效果。

附录A

在内共振幅频方程式(14)中

其中:

B1=2b1a2k2-1k2-2

B2=2b1b2k2-1k3-1

附录B

在静态分岔方程式(22)中

附录C

在标准式线性化矩阵B的特征方程式(28)中