混合联肢PEC墙结构基于合理失效模式的性能化设计方法研究

周巧玲, 赵仕兴, 苏明周, 石 韵

(1．四川省建筑设计研究院有限公司,成都 610041;2．西安建筑科技大学 土木工程学院,西安 710055;3.西安石油大学 土木工程学院,西安 710065)

传统的基于承载力和延性的抗震设计方法,基本实现了结构“大震不倒”安全目标,保证了人员生命安全,但控制不了其在地震作用下的破坏程度,造成的经济损失和需要的修复时间可能远超社会承受限度。随抗震设计理论的发展及公众和社会对建筑抗震要求的提高,抗震设计目标由“大震不倒”转变为“控制地震经济损失、保证结构使用功能的延续等使用性能目标”。在此背景下,基于性能的抗震设计理论逐渐形成。Bertero[1]首先提出基于性能的抗震设计理论,该设计理论的核心思想是:保证设计的工程结构或构件在设计使用年限内能满足各种预定性能目标,而具体性能目标则由使用功能、结构重要性和业主自身要求来确定[2-3]。基于性能的抗震设计理论提出后,首先在基于位移的抗震设计方法中得到实践和发展。但基于位移的抗震设计方法仅用位移作为结构抗震性能评估指标,不足以对结构弹塑性阶段的破坏特征和抗震性能进行全面描述,无法考虑持时对结构造成的累积损伤。为了考虑结构的累积损伤效应,在位移指标的基础上加入能量指标,即基于能量的抗震设计方法。其基本思想来源于能量平衡,只要结构通过阻尼和滞回耗散的能量大于地震输入的能量,结构就能有效抵抗地震作用,不发生倒塌[4]。基于能量的抗震设计通过控制结构的耗能机制和损伤模式,实现了对结构耗能分布的有效控制和抗震性能的整体把握。Leelataviwat等[5]提出的基于性能的塑性设计方法是一种基于能量的设计方法。该法直接考虑结构非弹性性能,已成功应用于菱形网格支撑框架[6]、联肢钢板剪力墙[7]、FRC对角斜筋连梁联肢剪力墙[8]以及混合联肢剪力墙[9]等多种结构体系中。

结合混合联肢剪力墙结构体系的概念以及型钢部分外包混凝土组合剪力墙(partially encased composite shear wall,PEC剪力墙)抗震性能优异、装配化程度高等优点[10],Zhou等[11-14]提出了一种新型混合联肢PEC墙结构,即采用PEC墙肢代替传统钢筋混凝土墙肢。针对该新型混合联肢PEC墙结构,开展了系列研究。结果表明,混合联肢PEC墙结构滞回曲线饱满而稳定,延性性能好,耗能能力强;与已有联肢墙结构研究成果一致,耦连比是影响混合联肢PEC墙结构整体性能的控制因素,为保证混合联肢PEC墙结构形成合理失效模式,塑性耦连比(CRp)取值范围应控制在27%～54%。

虽现行GB 50011—2010《建筑抗震设计规范》[15](以下简称“抗规”)中引入了建筑抗震性能化设计的相关条文,但由于对结构弹塑性地震反应分析存在困难,目前的结构抗震设计仍然以采用基于力和相应的构造及内力调整措施来保证结构延性的设计方法为主。具体而言,结构设计主要分两阶段进行,首先按弹性计算方法,确定小震作用下结构的承载力,然后进行大震作用下的弹塑性变形验算。在对传统钢筋混凝土联肢墙结构进行抗震设计时,目前规范主要通过控制连梁的抗震性能,来保证结构整体的抗震性能,并未从结构整体出发进行考虑。而混合联肢PEC墙结构中的钢连梁与钢筋混凝土连梁存在较大差异,如果简单套用规范中的方法对混合联肢PEC墙结构进行抗震设计难以保证其抗震性能。

为解决上述问题,本文基于性能化设计概念,研究混合联肢PEC墙结构基于合理失效模式的性能化设计方法,并给出完整设计流程。最后采用基于合理失效模式的性能化设计方法对12层混合联肢PEC墙结构进行算例设计,并对算例进行Pushover分析和弹塑性动力时程分析评估其抗震性能,验证混合联肢PEC墙结构基于合理失效模式的性能化设计方法的可行性。

1 基于合理失效模式的性能化设计方法

1.1 合理失效模式

依据文献[13]可知,CRp在27%～54%之间的混合联肢PEC墙结构抗震性能好、失效模式合理。这种合理失效模式可表述为:在大震作用下,沿墙高布置的钢连梁首先顺序剪切屈服耗散能量,并承担主要耗能工作,延缓PEC墙肢的屈服,然后在PEC墙肢底部形成弯曲塑性铰耗散能量,塑性铰充分发展后达结构承载能力极限状态,如图1所示。此失效模式的合理性主要体现在以下两个方面:

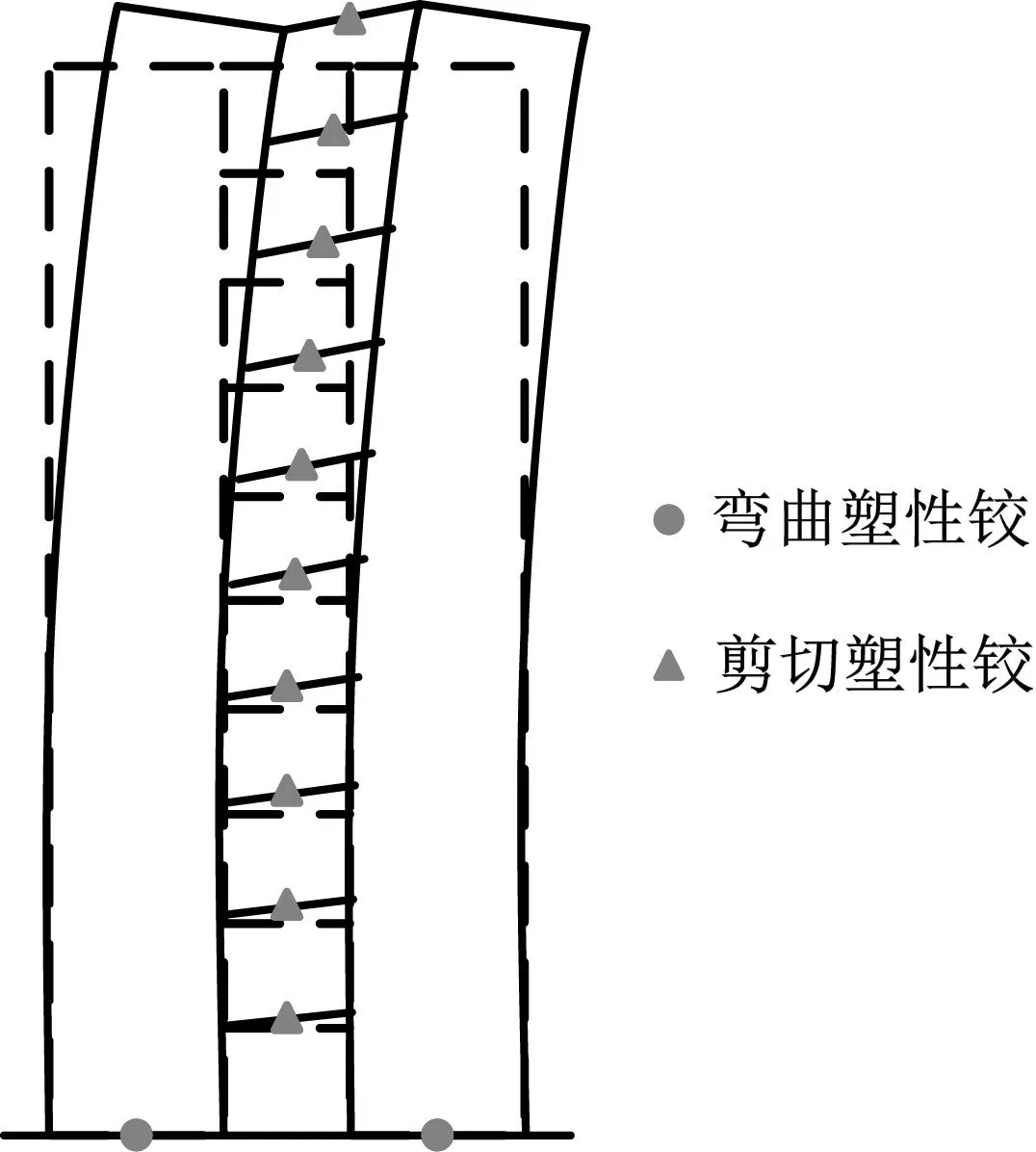
图1 混合联肢PEC墙结构合理失效模式Fig.1 Reasonable failure mode of hybrid coupled PEC wall

(1) 失效模式具有“有序”性,即混合联肢PEC墙结构中各构件的屈服按照预定顺序依次发生,使延性好、耗能能力强的钢连梁首先屈服耗能,保护结构中的关键构件(PEC墙肢),延缓其屈服,减轻其损伤。

(2) 失效模式具有“渐近”性,即混合联肢PEC墙结构的抗震具有层次性,不会因某部分构件屈服而出现刚度大幅降低的情况。

1.2 性能目标

依据我国抗规中的三水准抗震设防目标,结合上述关于混合联肢PEC墙结构合理失效模式的定义,在基于合理失效模式的性能化设计中,对混合联肢PEC墙结构中各构件的性能目标表述如下:

(1) 小震作用下钢连梁和PEC墙肢均处于弹性状态。

(2) 中震作用下大部分钢连梁进入塑性状态,但屈服程度低,而PEC墙肢基本不屈服,仍然处于弹性阶段。震后修复主要集中于钢连梁。

(3) 大震作用下沿墙高布置的钢连梁大量屈服,且屈服程度较高,承担主要耗能,PEC墙肢底部也进入塑性状态,开始辅助耗能。

2 目标位移角

目标位移角作为基于合理失效模式的性能化设计方法中的重要参数,其值准确性直接影响结构设计基底剪力准确性,进而影响设计结构合理性。而不同抗侧力结构,目标位移角均存在差异。对于本文提出的混合联肢PEC墙结构体系,鉴于其变形能力介于钢筋混凝土结构与纯钢结构之间,参考JGJ/T 380—2015《钢板剪力墙技术规程》[16]3.4节对钢板组合剪力墙变形限值要求,取混合联肢PEC墙结构弹性和弹塑性层间位移角限值分别为1/400和1/80。同时依据抗规附录M条文说明,对结构在不同破坏状态下变形参考值与其弹性和弹塑性层间位移角间关系的描述,可取混合联肢PEC墙结构在不同破坏状态下的层间位移角限值如表1所示。结合1.2节混合联肢PEC墙结构从承载力角度所取性能目标,从变形角度的性能目标为:①中震作用下,混合联肢PEC墙结构的最大层间位移角不大于1/130;②大震作用下,混合联肢PEC墙结构的最大层间位移角不大于1/90。

表1 混合联肢PEC墙结构不同破坏状态下的层间位移角限值Tab.1 Limits of inter-story drift ratio for hybrid coupled PEC wall under different failure states

2.1 设计基底剪力

基于合理失效模式的性能化设计依据能量守恒定律[17],将结构单向推覆至目标位移,结构达合理失效模式时,外力所做功应等于等效理想弹塑性单自由度体系(EPP-SDOF)达相同状态时所需能量,EPP-SDOF的最大地震输入能则可用多个等效弹性单自由度体系(E-SDOF)最大地震输入能之和EI的γ倍来表征,γ为最大地震输入能修正系数,如图2所示。

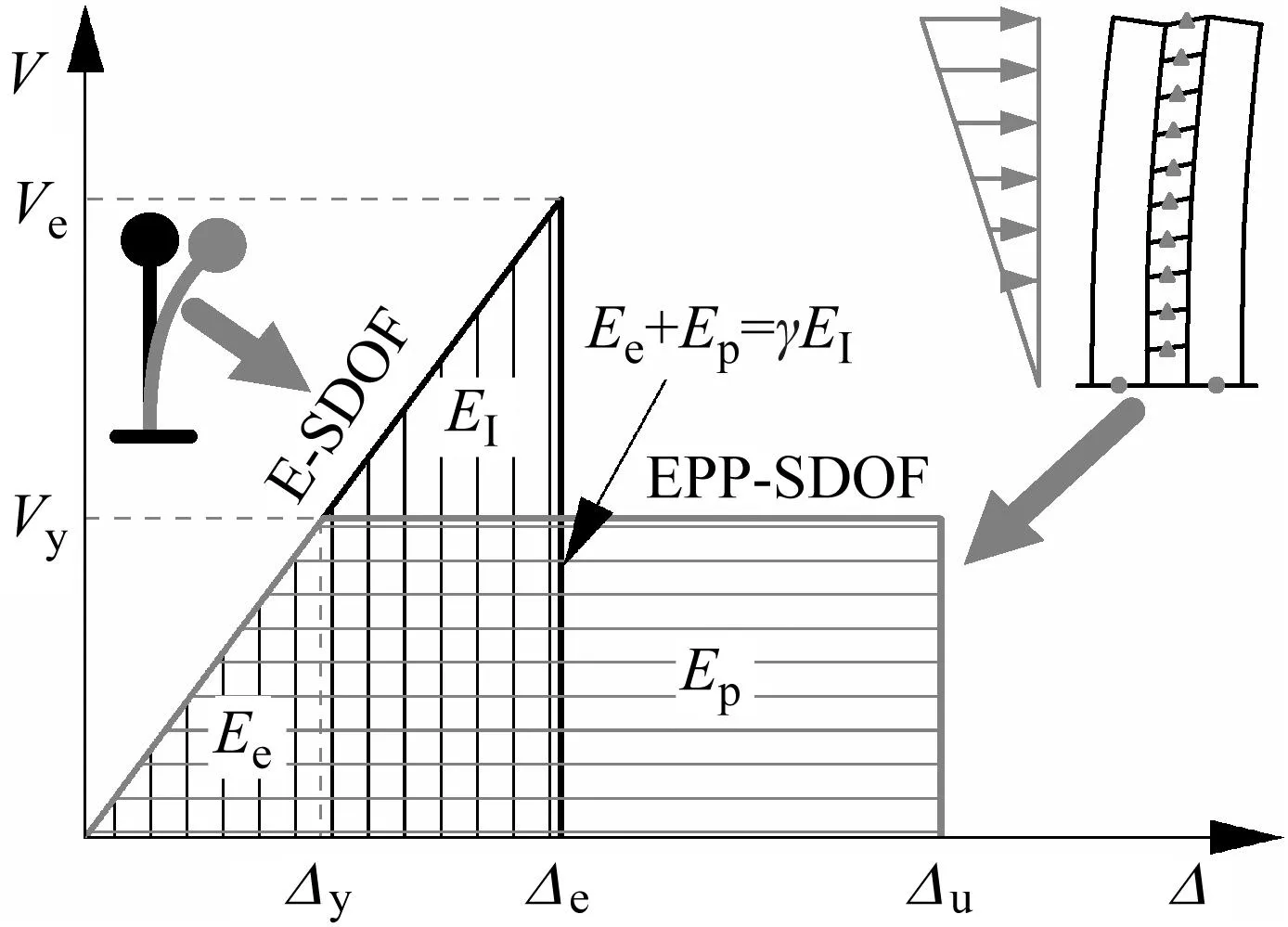
图2 能量平衡概念Fig.2 Concept of energy balance

考虑到上述假定中,将结构的能力曲线假定为理想弹塑性,且在单向推覆分析中无法考虑结构滞回性能。而混合联肢PEC墙结构的滞回曲线与理想弹塑性结构的滞回曲线还存在差异,因此,白久林[18]提出了考虑结构不同滞回特性的能量平衡方程,引入折减系数η修正结构累积滞回耗能Ep

Ee+ηEp=γEI

(1)

其中

(2)

式中:η为滞回耗能修正系数;A1和A2分别为结构实际滞回环面积及其对应的EPP-SDOF滞回环面积,如图3所示。

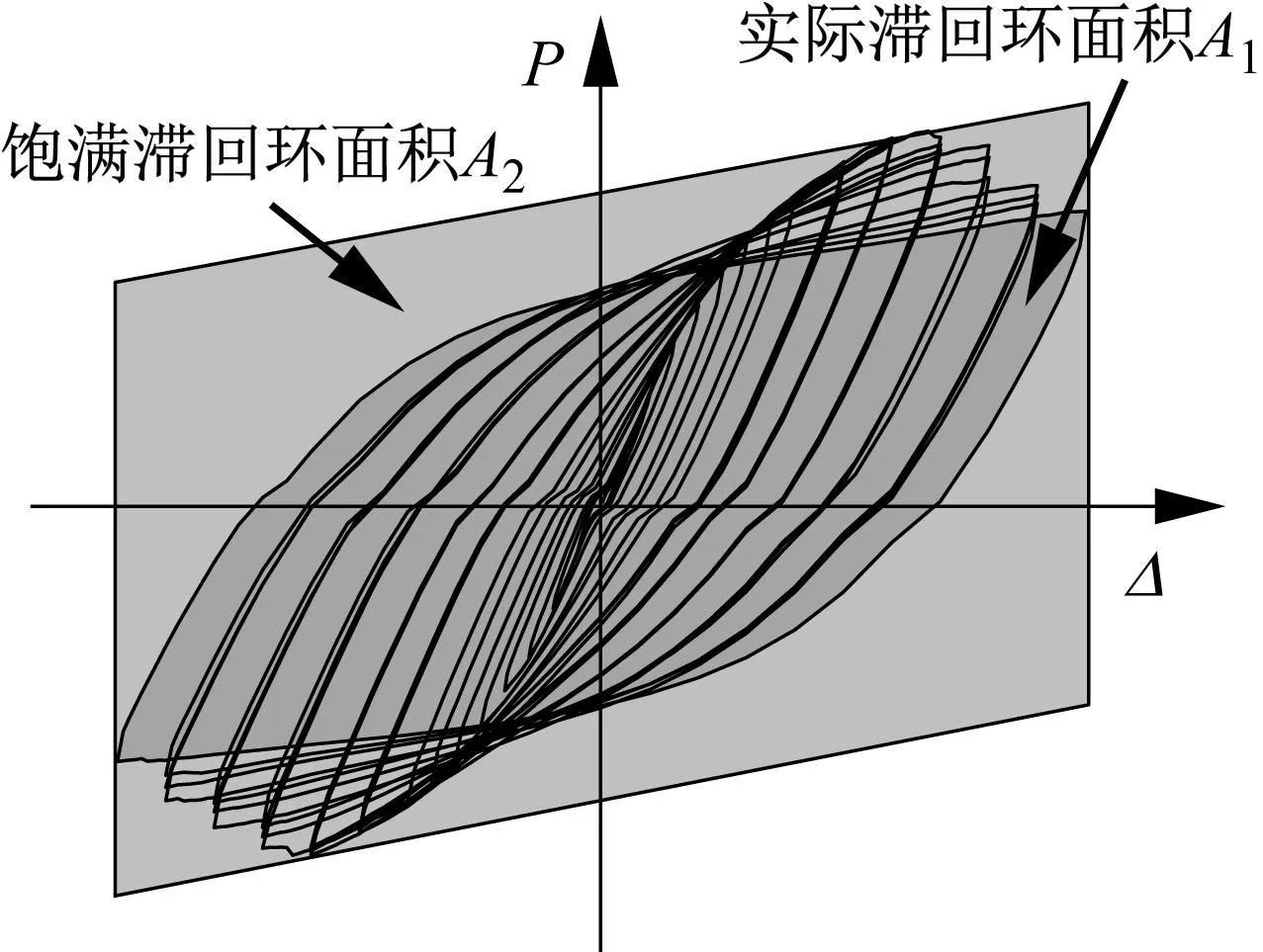
图3 滞回耗能修正系数计算Fig.3 Calculation for correction coefficient of hysteretic energy dissipation

白久林指出,钢筋混凝土剪力墙结构的滞回耗能修正系数η可采用Small Takeda模型计算,当结构等效周期大于1 s时,可取为定值0.588。鉴于本文的混合联肢PEC墙结构等效周期大于1 s,且滞回性能优于钢筋混凝土剪力墙结构,偏于保守的取η为0.588。

对于最大地震输入能修正系数γ,由式(1)可得

(3)

则

(4)

其中

(5)

(6)

式中:Ve和Δe分别为E-SDOF的基底剪力和侧向位移;Vy、Δy及Δu分别为EPP-SDOF的基底屈服剪力、屈服位移及目标位移;μΔ和Rμ分别为结构的延性系数和延性折减系数。

由上述分析可知,最大地震输入能修正系数与延性系数和延性折减系数直接相关。针对延性系数、延性折减系数及自振周期三者关系,国内外学者进行了系统研究,本文采用Newmark等[19]提出的关系式,如表2所示。

表2 不同T范围内μΔ和Rμ的关系Tab.2 Relationship between μΔ and Rμ within different range of T

给定地震水准作用下,EPP-SDOF最大地震输入能γEI可表示为

(7)

式中:M为结构等效总重量;Sv和Sa分别为谱速度和谱加速度;T为结构基本自振周期;g为重力加速度。

对于弹性振动能Ee,基于Akiyama[20]的研究,可采用下式计算

(8)

式中,G为结构总重力荷载代表值。

由前述假定可知,结构的累积滞回耗能Ep等于作用于结构的侧向力在结构屈服后所做的功,对于如图1所示合理失效模式有

(9)

式中:Fi=λiVy为结构第i层的水平地震作用,λi为楼层侧向力分布系数,计算方法见2.2节;Hi为结构第i层离地面的高度;θp为结构塑性位移角,按下式计算

θp=θu-θy

(10)

式中,θu和θy分别为结构目标位移角和屈服位移角。

目标位移角θu的取值参看第2章。对于屈服位移角θy,依据文献[13]可知,CRp范围适中的混合联肢PEC墙结构,所有钢连梁屈服时位移角在1/351～1/204之间。故本文混合联肢PEC墙结构的屈服位移角θy取为1/200。

将式(7)、(8)和(9)代入能量平衡方程式(1),取M=G/g,得:

(11)

整理得

(12)

则:

(13)

式中,w为无量纲参数,采用下式计算

(14)

且

(15)

2.2 侧向力分布

侧向力分布模式是否准确反映结构在地震作用下的层剪力分布情况,直接决定了设计结构的合理性,而现行规范给出的侧向力分布模式基于弹性分析建立,不能准确反映结构进入塑性状态后的受力情况。Chao等[21]基于大量的非线性动力时程分析结果,研究了不同类型结构体系弹塑性响应,提出了一种新的侧向力分布模式,该侧向力分布模式能更精确地反映结构在塑性状态下的层剪力分布,并考虑结构高阶振型影响。本文采用该侧向力分布模式

(16)

(17)

式中:βi为楼层剪力分布系数;α为与结构体系有关的无量纲参数,参考文献[22]本文α取为0.6;Gj和Gn分别为第j层和结构顶层的重力荷载代表值;Vi和Vn分别为结构第i层和顶层的层剪力。

3 构件设计

基于合理失效模式的性能化设计方法,以整体结构达目标位移时实现合理失效模式为主要控制目标。对于混合联肢PEC墙结构,合理失效模式见图1。非弹性变形集中于沿墙高布置的钢连梁及PEC墙肢底部截面,二者成为塑性设计中的关键构件。依据功能关系,外荷载功等于内力功,同时由于钢连梁发生反对称变形,重力荷载所做外力功等于零,则:

(18)

式中:Mpw为各PEC墙肢底部截面的塑性抗弯承载力之和;Vpb,i为第i层钢连梁的塑性抗剪承载力;b为钢连梁净跨度;γp为钢连梁塑性转角,且γp=(L/b)θp,L为两PEC墙肢形心线的间距。

3.1 钢连梁设计

为对钢连梁截面进行设计,首先要得到各层钢连梁剪力需求。依据耦连比定义,基于选定目标CRp,钢连梁的总剪力需求为

(19)

式中:MOTM为结构底部总倾覆力矩;Vb,i为结构第i层钢连梁的剪力需求。

所有钢连梁的总剪力需求确定后,由式(20)得到各层钢连梁的剪力需求[23]

(20)

确定了各层钢连梁的剪力需求后,便可按相关规范对其截面进行设计。由文献[13]可知,混合联肢PEC墙结构中的钢连梁与偏心支撑钢框架中的耗能梁段受力性能相似,在地震作用下首先剪切屈服耗散能量。故可按我国JGJ 99—2015《高层民用建筑钢结构技术规程》[24]中有关偏心支撑耗能梁段的相关条款进行设计。

3.2 PEC墙肢底部加强区截面设计

在确定了混合联肢PEC墙结构中,由钢连梁耦连作用抵抗的倾覆力矩后,即可通过式(18)计算得到PEC墙肢底部截面所抵抗的倾覆力矩Mpw,该倾覆力矩应该按一定比例分配给受拉和受压侧PEC墙肢承担,分配比例如表3所示。

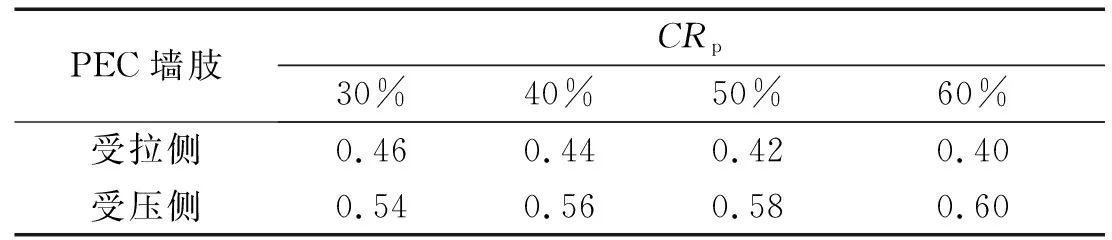
表3 混合双肢PEC墙力矩分配比例Tab.3 Moment distribution ratio of hybrid coupled PEC wall

为保证实现“强墙肢弱连梁”的合理失效模式,在对PEC墙肢底部加强区截面进行设计时,考虑钢连梁屈服后的强化,对按上述分配得到的PEC墙肢底部加强区截面弯矩乘超强系数γw

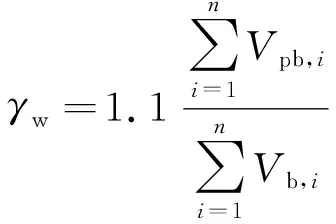
(21)

式中,Vpb,i和Vb,i分别为第i层钢连梁的塑性抗剪承载力和塑性抗剪承载力需求。

Paulay等[25]研究发现,受高阶振型的影响,地震作用下剪力墙结构的最大动态基底剪力远大于设计基底剪力,故为保证剪力墙的破坏仍以延性较好的弯曲变形为主,Paulay等引入了一个动态剪力修正系数ω对剪力墙结构设计基底剪力进行修正

(22)

本文对混合联肢PEC墙结构进行设计时采用上述ω考虑高阶振型的影响。

3.3 PEC墙肢非加强区截面设计

对PEC墙肢非加强区截面进行设计时,可将混合联肢PEC墙结构沿钢连梁中部切开,成为独立的左右两侧PEC墙肢隔离体,如图4所示。对两侧墙肢隔离体进行受力分析时,为保证静力平衡,有如下假定:①各层钢连梁都达到其极限状态,即钢连梁发生剪切屈服达到其塑性抗剪承载力;②墙肢底部截面也达到不考虑超强系数下的塑性抗弯承载力;③两侧墙肢的侧向力分布模式与设计侧向力分布模式保持一致。则受拉侧和受压侧PEC墙肢的基底剪力可按下式计算

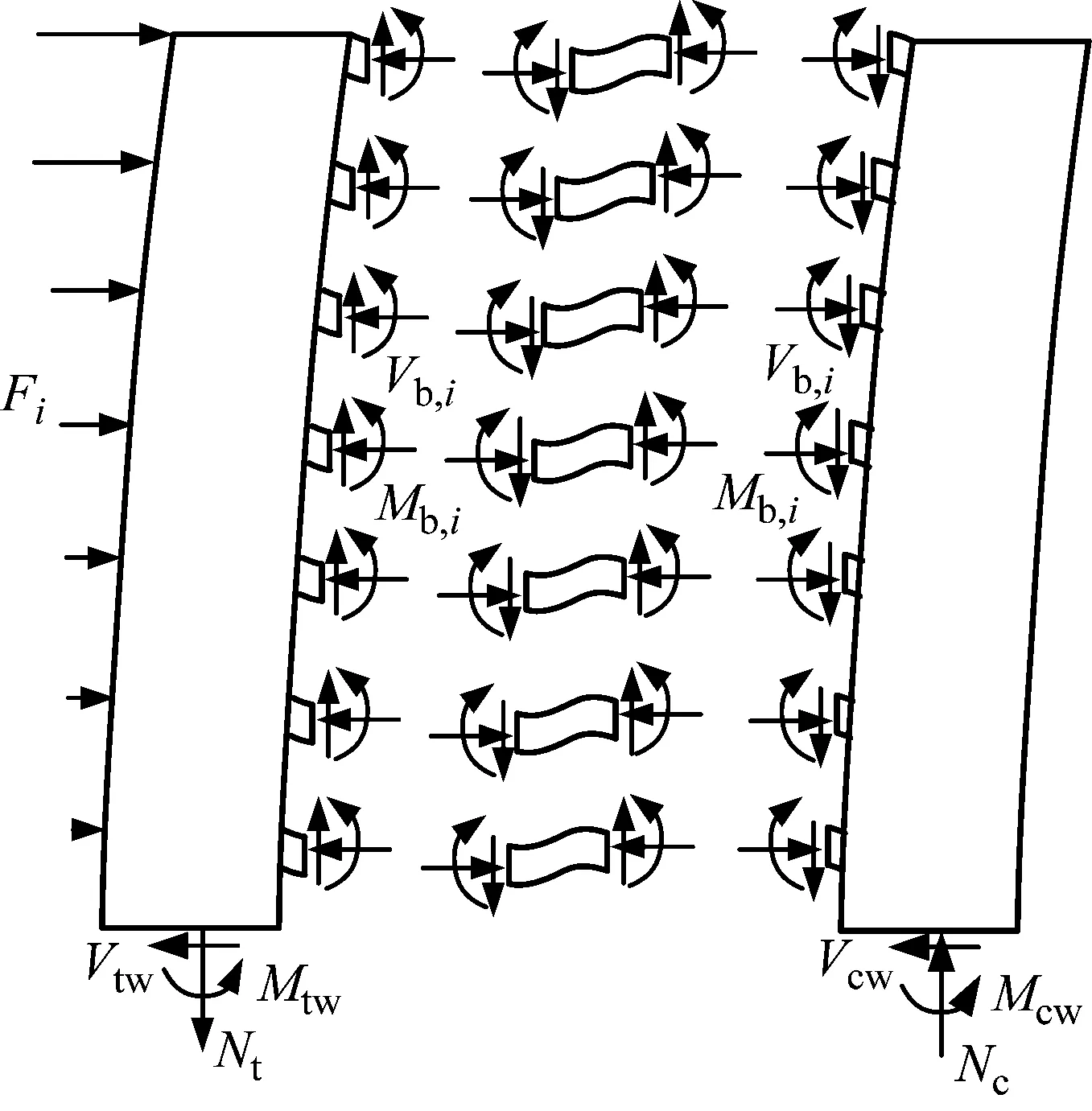
图4 混合联肢PEC墙结构隔离体示意图Fig.4 Free body diagram of hybrid coupled PEC wall

(23)

(24)

式中:hw为PEC墙肢的截面高度;Mb,i=Vpb,i×b/2为钢连梁剪切屈服时的端部弯矩。

获得两侧墙肢的基底剪力后按2.2节侧向力分布模式对其进行分配,得到两侧墙肢每层的侧向力,结合每层钢连梁端部弯矩和剪力即可计算得到两侧墙肢每层弯矩和剪力,最后按文献[26]给出的承载力计算公式进行PEC墙肢截面设计。

4 混合联肢PEC墙结构基于合理失效模式的性能化设计步骤

(1) 依据设计地震水准及性能目标,确定结构合理失效模式及目标位移角θu,结合结构屈服位移角θy,计算得到结构塑性位移角θp和延性系数μΔ。

(2) 依据GB 50009—2012《建筑结构荷载规定》[27]估算结构基本自振周期T,按表2计算延性折减系数Rμ及最大地震输入能修正系数γ。

(3) 基于(1)、(2)步确定的设计参数和给定地震水准下的设计谱加速度Sa,利用式(13)即可求得结构的设计基底剪力Vy。

(4) 按式(16)确定结构设计用侧向力Fi及其分布,由下式计算得到结构底部总倾覆力矩

(25)

(5) 选择目标CRp,分别由式(19)、(20)计算所有钢连梁的总剪力需求和各层钢连梁的剪力需求。

(6) 将第(5)步中确定的钢连梁剪力需求代入式(18),求出PEC墙肢底部截面所需抵抗的总倾覆弯矩Mpw,并依据表3在受拉和受压侧PEC墙肢中进行分配。

(7) 依据静力平衡条件,分别由式(23)和(24)计算得到受拉侧和受压侧PEC墙肢基底剪力Vtw和Vcw,并沿高度按式(16)进行分配。

(8) 结合每层钢连梁端部的剪力、弯矩以及第(7)步中分配给受拉侧和受压侧PEC墙肢每层的侧向力,计算受拉侧和受压侧PEC墙肢每层的剪力和弯矩。

(9) 对钢连梁和PEC墙肢底部加强区截面按式(26)进行承载力计算,对PEC墙肢非加强区截面按式(27)进行承载力计算。

SGE+SEk≤Rk

(26)

γGSGE+γESEk≤R/γRE

(27)

式中:SGE为重力荷载代表值效应;SEk为水平地震作用标准值效应;Rk和R分别为按材料标准值计算的承载力和按材料设计值计算的承载力;γG和γE分别为重力荷载分项系数和水平地震作用分项系数;γRE为抗震承载力调整系数。

(10) 采用塑性方法设计钢连梁和PEC墙肢底部加强区截面,采用弹性设计方法设计PEC墙肢非加强区截面。对于PEC墙肢截面,采用文献[26]提出的简化力学分析模型和承载力计算公式进行计算。

图5给出了混合联肢PEC墙结构基于合理失效模式的性能化设计流程图,便于更直观地理解其计算过程。

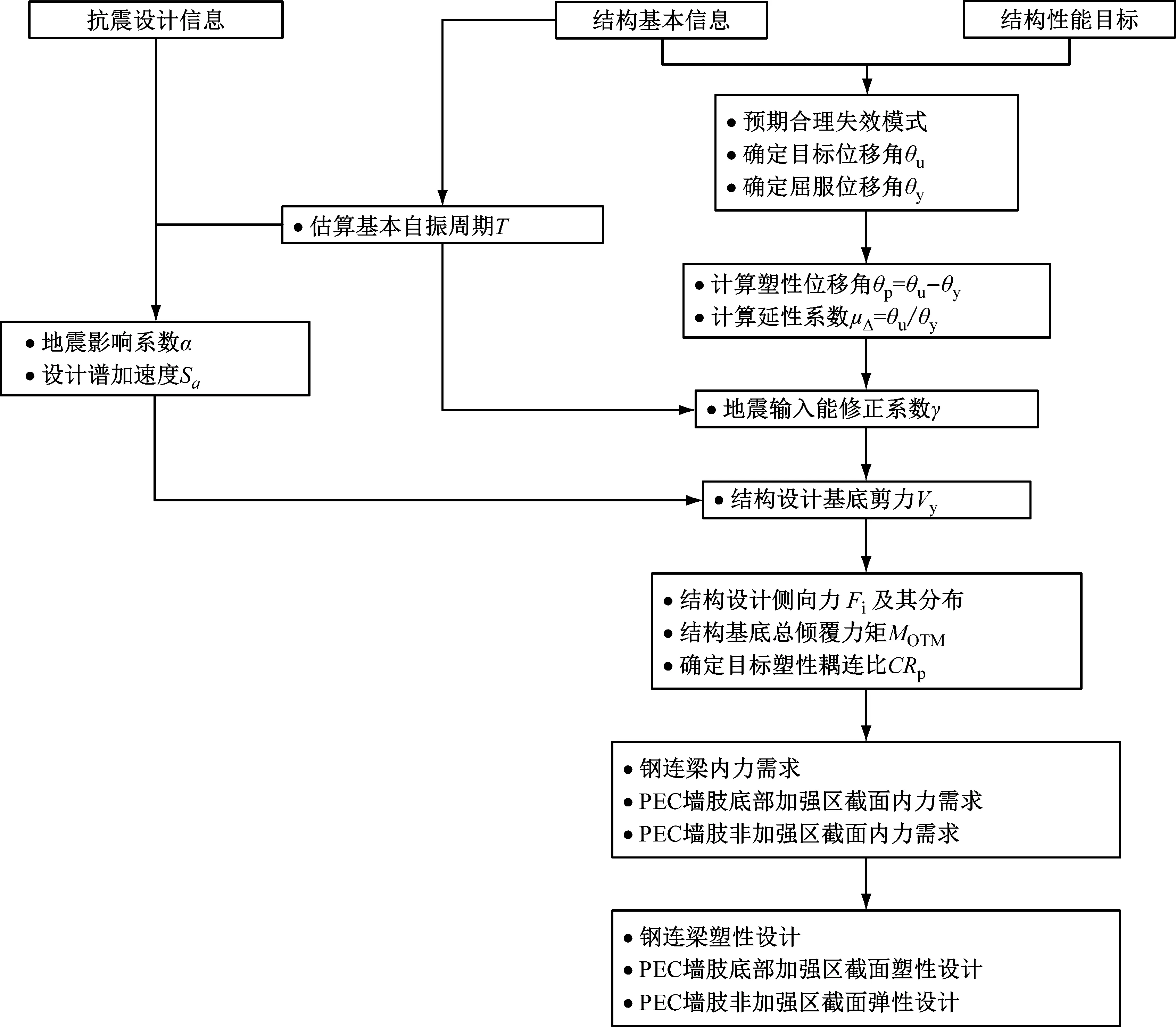
图5 混合联肢PEC墙结构基于合理失效模式的性能化设计流程Fig.5 Performance-based design method flow chart of the hybrid coupled PEC wall based on the reasonable failure mode

5 算例设计及分析

为验证基于合理失效模式的性能化设计方法的有效性及适用性,本节采用上述设计方法设计了12层混合联肢PEC墙结构算例,并利用ABAQUS对其进行Pushover分析和动力弹塑性时程分析。

5.1 工程概况

该12层混合联肢PEC墙结构平面布置如图6所示。PEC墙肢长3 m,钢连梁跨度为1 m,两者厚度均为0.25 m。结构位于抗震设防烈度8度(0.2g)地区,总高36 m,每层均为3 m。设计地震分组为第二组,场地类别为Ⅱ类。PEC墙肢内钢板和钢连梁钢材均为Q345B;U型-横向拉结筋为HRB400;混凝土强度等级为C40;每层集中重力荷载代表值为1 200 kN。

图6 算例平面布置(mm)Fig.6 Plane layout of model (mm)

5.2 算例设计

表4给出了算例结构基于合理失效模式的性能化设计方法中震和大震作用下的主要设计参数。由表可知,大震作用下算例结构的设计基底剪力Vy为中震作用下的1.360倍,故本文算例结构设计以性能目标为1/90控制。

确定结构的控制作用及Vy后,按式(16)给出结构侧向力及其分布,然后按式(25)计算得到MOTM,并通过目标CRp确定钢连梁总剪力需求及拉/压侧PEC墙肢底部弯矩。取CRp=40%,则算例结构在大震作用下各部分内力需求如表5所示。确定结构各部分内力需求后,便可按第3章对各构件进行设计。设计的混合联肢PEC墙结构的PEC墙肢和钢连梁截面尺寸如图7和表6所示。

表5 算例结构各构件内力需求Tab.5 Internal force demand of components

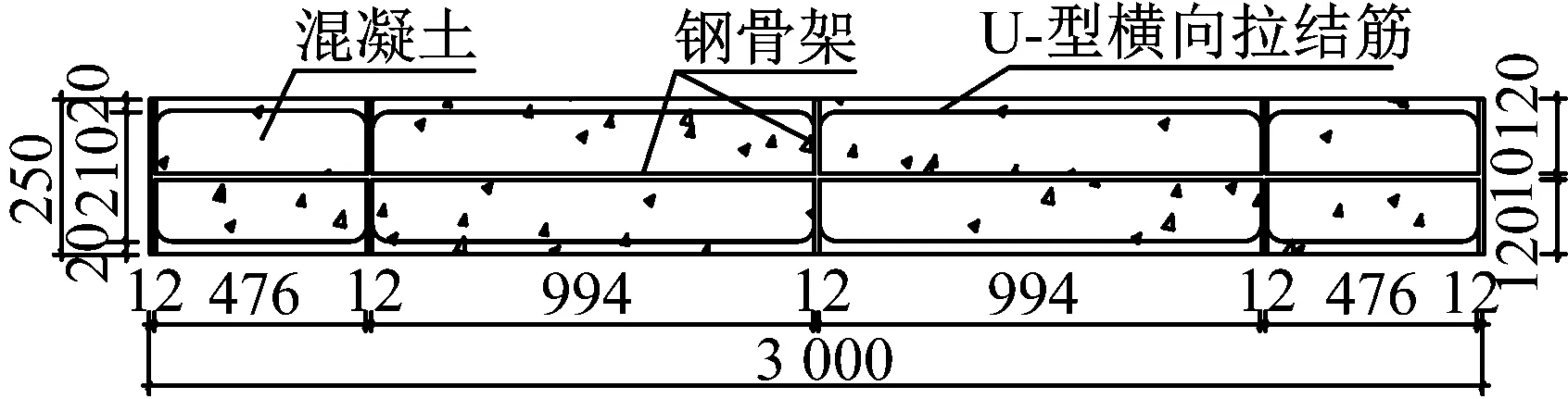
图7 PEC墙肢截面尺寸Fig.7 Section size of PEC wall pier

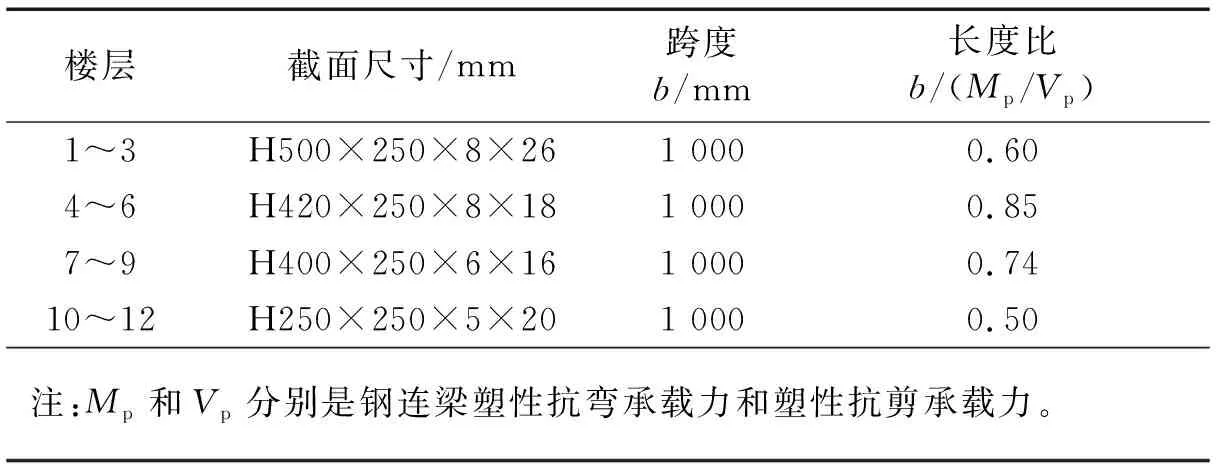
表6 钢连梁截面尺寸Tab.6 Section size of steel coupling beams

5.3 有限元模型建立和验证

在ABAQUS中建立算例结构的有限元模型。混凝土采用实体单元C3D8R进行模拟,型钢采用壳单元S4R进行模拟,横向拉结筋采用可考虑横向剪切变形的梁单元B31模拟。钢材采用线性随动强化模型,强化模量取为0.01;混凝土采用塑性损伤模型,塑性特征参数如表7所示。单轴应力-应变关系则参考GB 50010—2010《混凝土结构设计规范》[28]附录C。钢连梁与墙肢型钢内翼缘的对接焊缝采用“Tie”模拟,其余焊缝则采用“Merge”模拟,横向拉结筋通过“Embedded”嵌入混凝土中,墙肢型钢与混凝土间的接触关系则采用 “General contact”模拟,法向为“Hard contact”,切向为“Penalty”摩擦因数取为0.4。

表7 混凝土塑性特征参数[29]Tab.7 Plastic characteristic parameters of concrete[29]

为验证有限元建模方法的准确性,对文献[12]中的混合联肢PEC墙试件进行建模分析。图8为试验和有限元分析得到的滞回曲线对比,二者滞回曲线形状相似,有限元模型滞回曲线基本能捕捉到试验滞回曲线的特征。图9为试验和有限元模型最终破坏模式对比,二者吻合程度较高,破坏均集中在钢连梁腹板和PEC墙肢底部。试验和有限元结果正、反向极限承载力误差分别为6.7%和2.2%,均低于10%。有限元建模方法准确可靠,可以用于模拟混合联肢PEC墙结构实际受力性能。

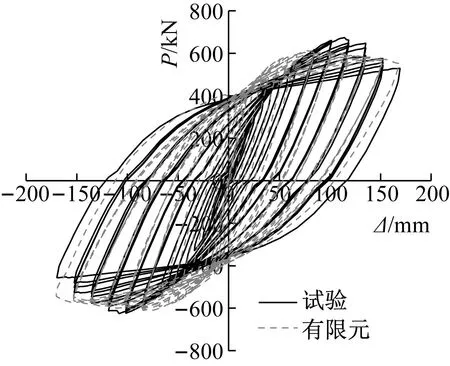
图8 滞回曲线对比Fig.8 Comparison of hysteretic curve

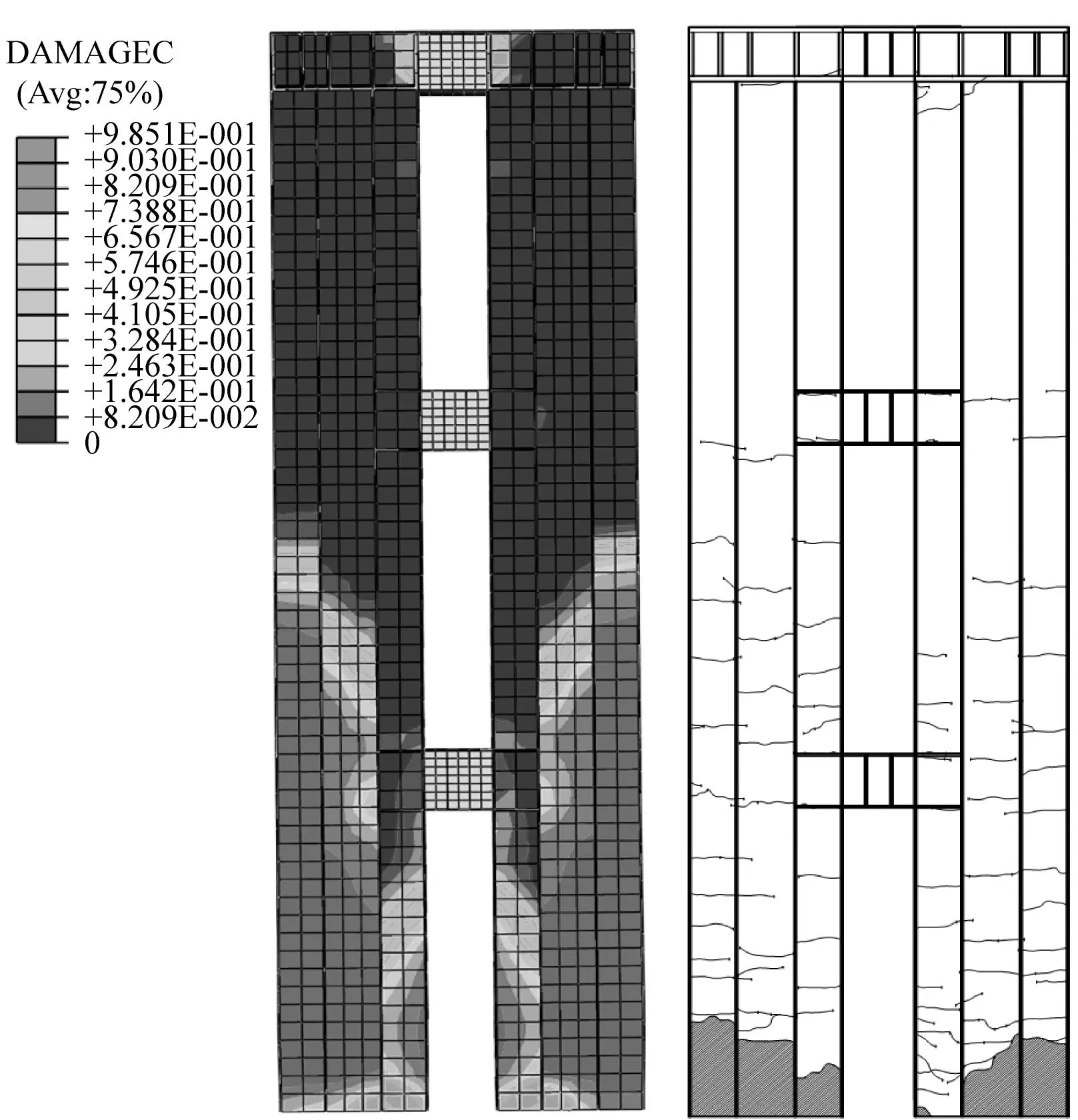
图9 破坏模式对比Fig.9 Comparison of failure mode

5.4 Pushover分析

(1) 推覆曲线

按1.5节给定的侧向力分布模式对算例结构有限元模型进行Pushover分析,得到的推覆曲线如图10所示。其上标注了“50%钢连梁腹板屈服”、“所有钢连梁腹板屈服”及“PEC墙肢底部型钢屈服”三状态对应的特征点。图11为特征点处结构的塑性铰分布情况。由图11可知,算例结构中部50%钢连梁腹板屈服时顶层位移角为1/449,小于给定结构屈服位移角1/200,而各层钢连梁腹板都发生剪切屈服时的顶层位移角达1/180,说明结构大部分钢连梁在中震作用下剪切屈服耗能,同时,算例结构PEC墙肢底部形成弯曲塑性铰的顶层位移角为1/114,大于中震作用下位移角需求1/130,即墙肢在中震作用下不屈服,在大震作用下才屈服,表明算例结构实现了合理失效模式,符合预定的性能目标。

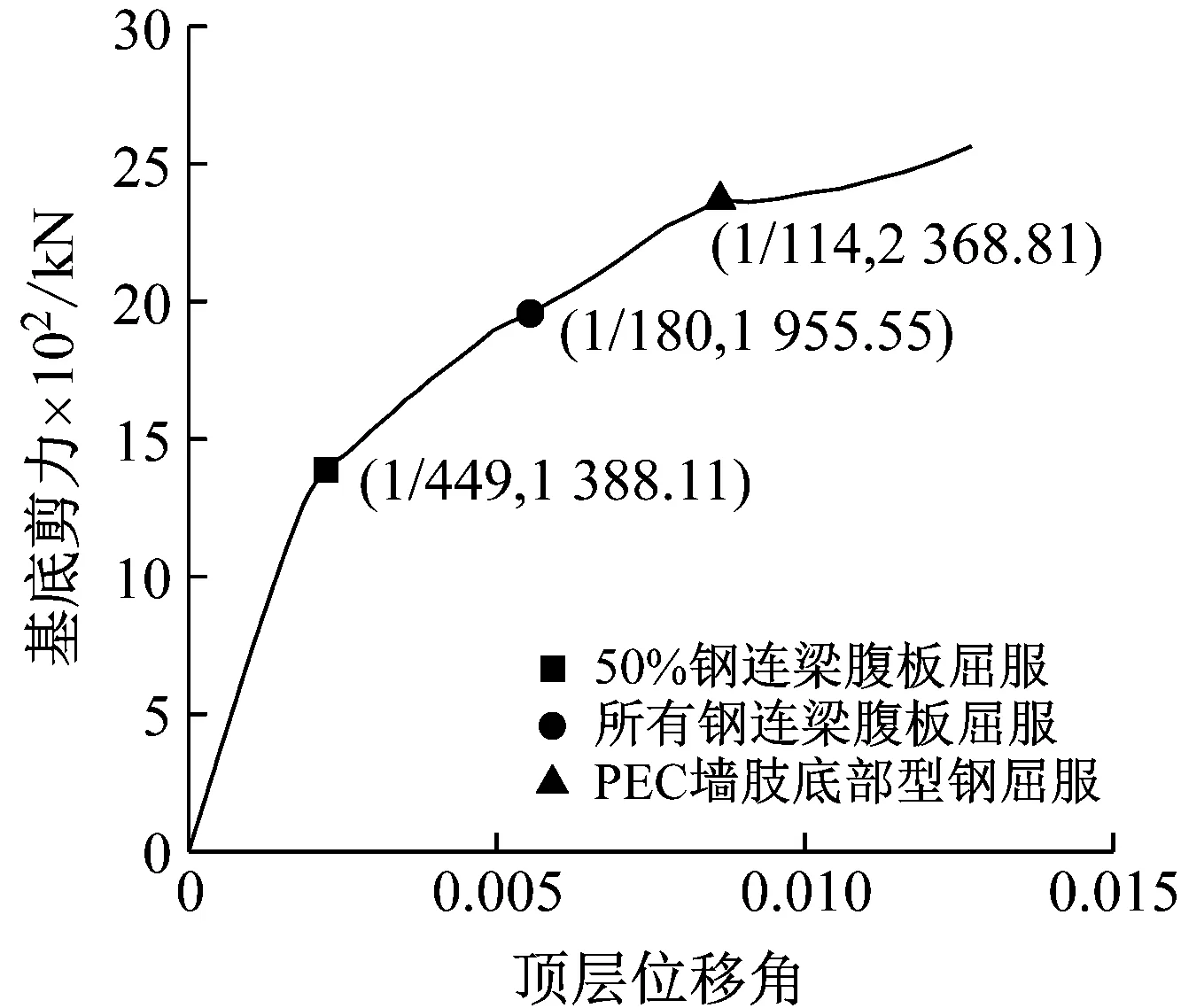
图10 推覆曲线Fig.10 Pushover curve

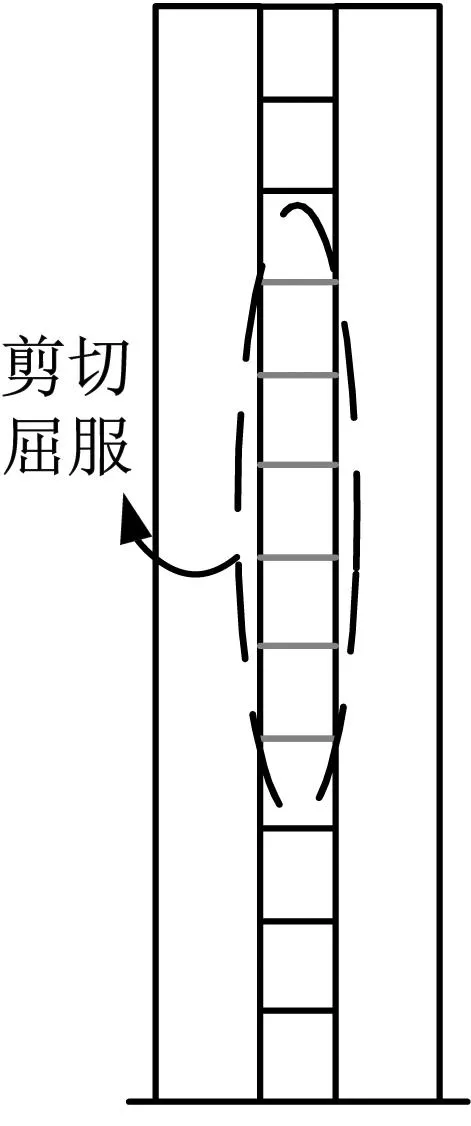
(a) 1/449

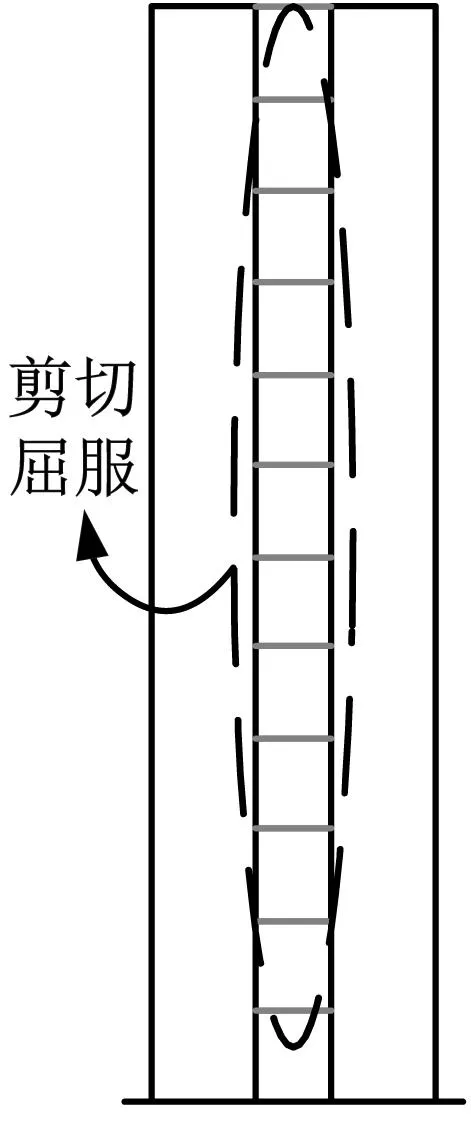
(b) 1/180

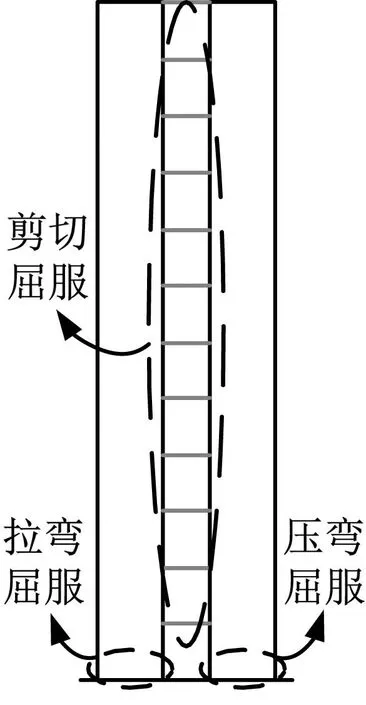
(c) 1/114图11 塑性铰发展过程Fig.11 Development of plastic hinges

总体来说,在Pushover分析中,算例结构首先在沿墙高布置的钢连梁中形成剪切塑性铰,然后随水平荷载增加,PEC墙肢底部外翼缘钢板开始进入塑性,水平荷载继续增加,墙肢底部屈服程度逐渐扩展向墙肢中上部延伸,最终形成弯曲塑性铰,结构达承载能力极限状态,与预期破坏模式相符。结构的破坏过程呈现良好的延性,沿墙高布置的钢连梁作为第一道抗震防线首先剪切屈服耗散能量,然后PEC墙肢作为第二道抗震防线底部形成弯曲塑性铰与钢连梁一起耗散能量,实现了“两阶段耗能体系”设计目标。

(2) 内力

图12给出了两侧PEC墙肢底部截面弯矩随结构顶层位移角的变化情况。加载初期,两侧墙肢抵抗的倾覆力矩接近,但随加载进行,由于墙肢混凝土开裂、钢连梁耦连作用等的影响,结构发生内力重分布,在顶层位移角达1/840后,二者承担的倾覆力矩比例发生改变,受压侧墙肢抵抗的力矩比例增加,受拉侧墙肢抵抗的力矩比例减小。当算例结构的顶层位移角达1/114,即各层钢连梁均已发生剪切屈服,两侧PEC墙肢底部也均形成弯曲塑性铰时,受拉侧墙肢与受压侧墙肢间抵抗倾覆力矩的比例约为:0.44∶0.56,与表3给出的力矩分配比例一致。

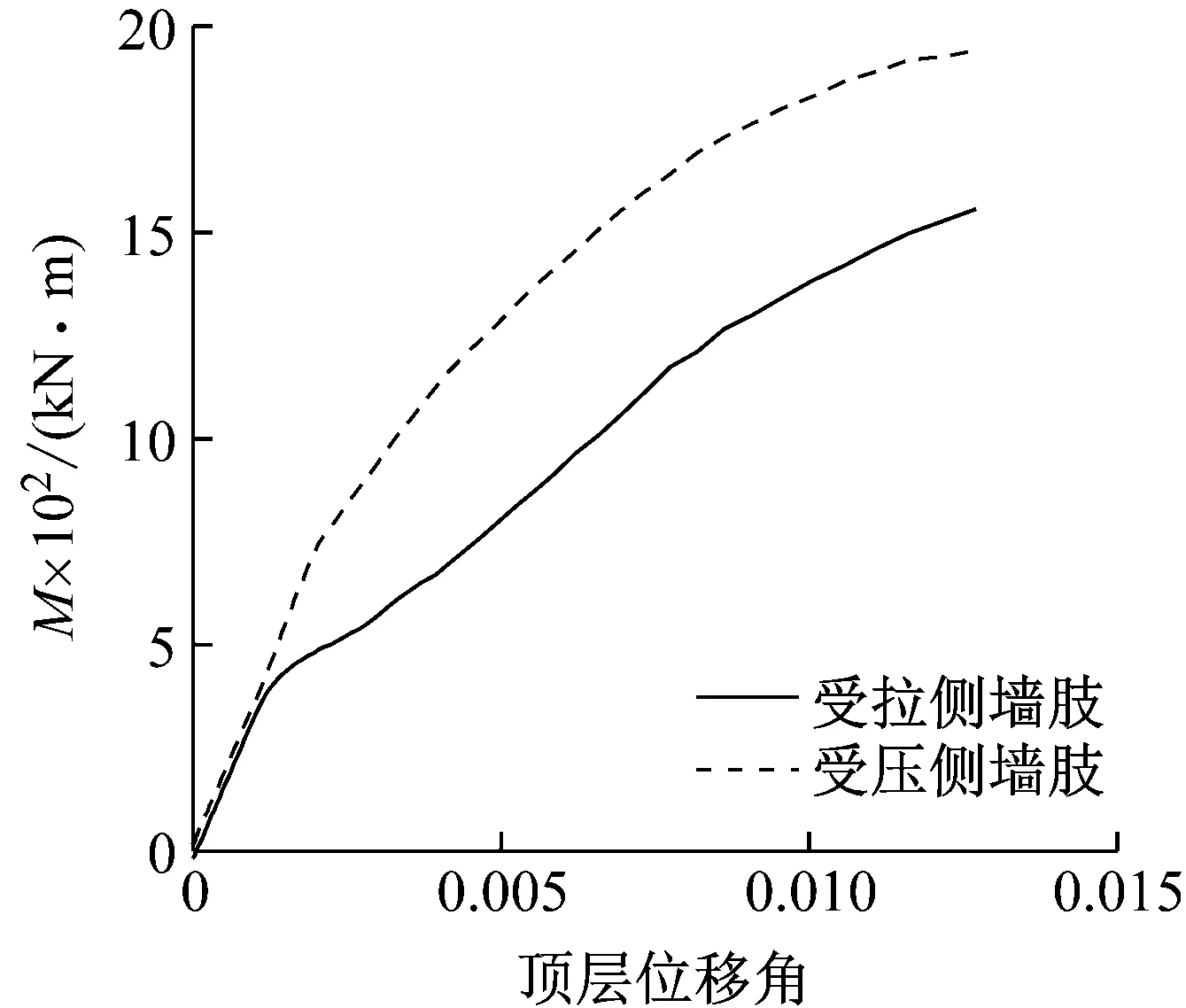
图12 PEC墙肢底面截面弯矩Fig.12 Bending moment of the bottom of PEC wall piers

图13为算例结构各特征点处钢连梁的剪力分布。由图13可知,不同阶段钢连梁剪力均呈中间大两边小的分布,与其他类型联肢墙结构连梁剪力分布类似;结构处于弹性状态(即50%钢连梁腹板屈服前)时,连梁剪力不均匀程度较高,随各构件开始屈服进入塑性状态,结构发生塑性内力重分布,连梁剪力不均匀程度逐渐降低。为更进一步研究钢连梁剪力分布情况,图14给出了算例结构各特征点处钢连梁归一化剪力(即各层连梁剪力/顶层连梁剪力)分布。由图14可知,中上部连梁归一化设计剪力与算例结构Pushover分析结果吻合较好,而下部尤其是底部连梁归一化设计剪力偏大,在弹性阶段,底层连梁归一化设计剪力为有限元结果的2.0倍,但在结构进入塑性后降至约1.2倍,证明本文采用的钢连梁剪力设计分布模式精度较高。故可偏于保守的基于层剪力分布系数βi确定的钢连梁剪力需求,进行混合联肢PEC墙结构中钢连梁的截面设计。

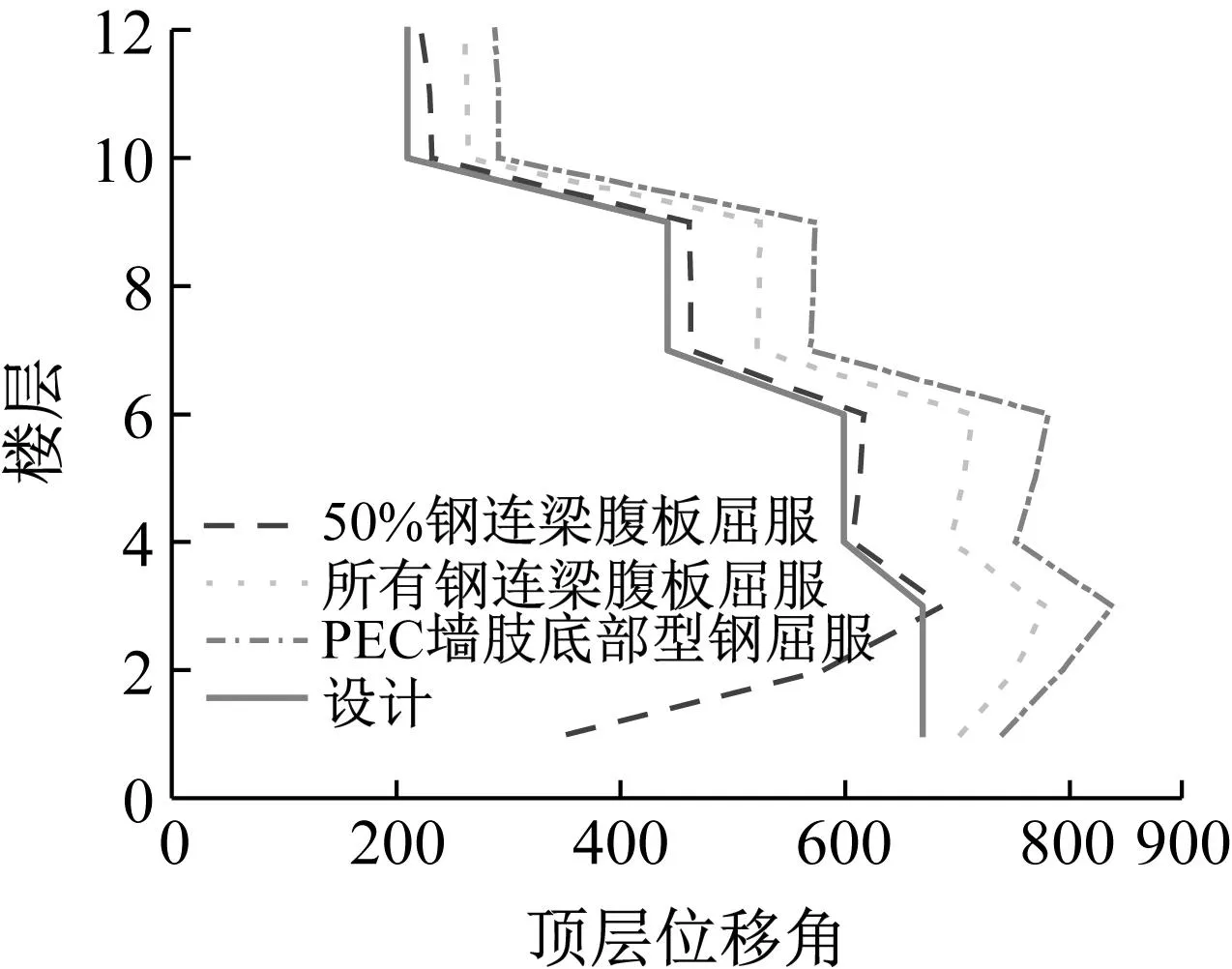
图13 钢连梁剪力分布Fig.13 Shear distribution of steel coupling beams

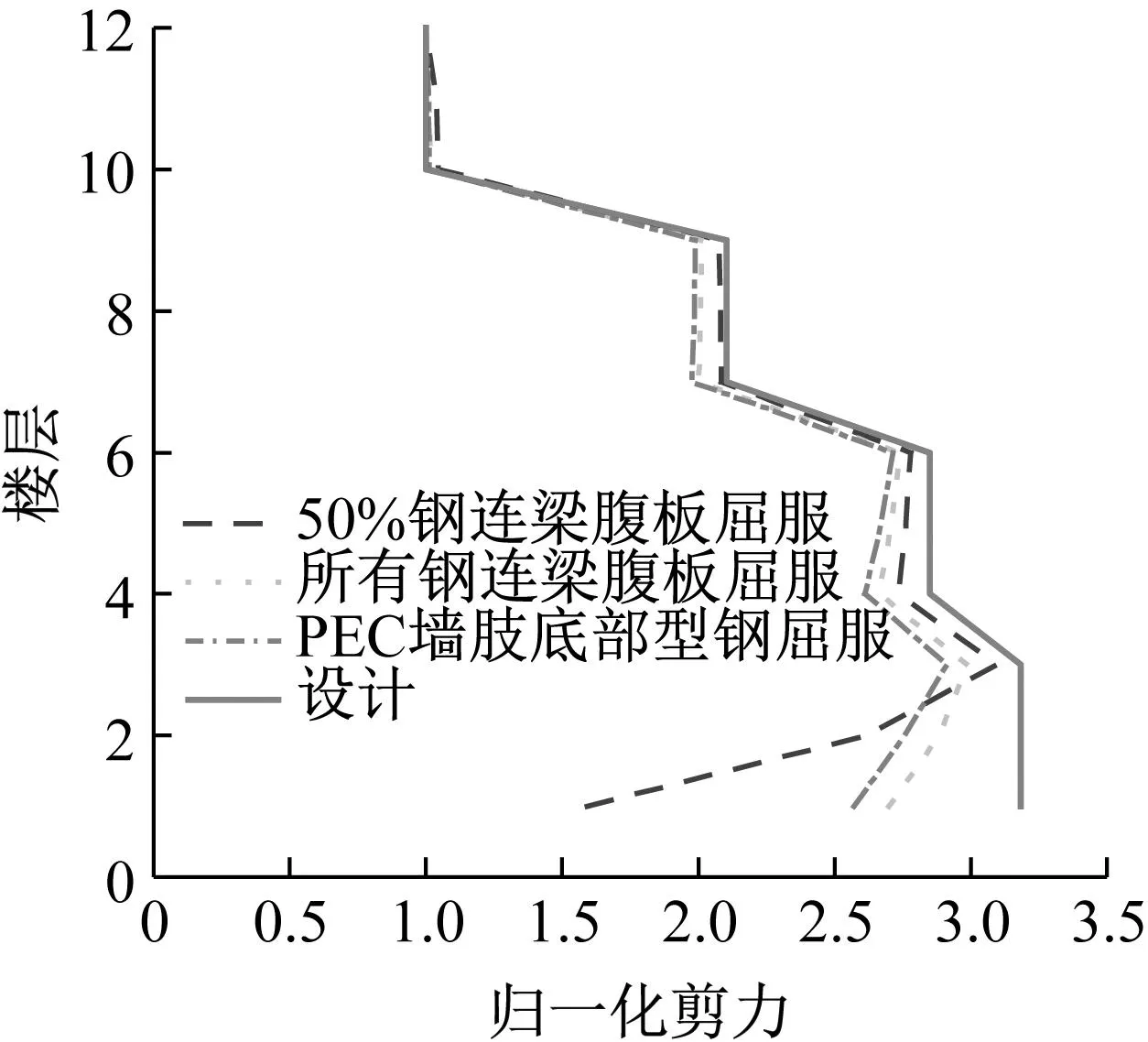
图14 钢连梁归一化剪力分布Fig.14 Normalized shear distribution of steel coupling beams

(3) 变形

图15给出了算例结构特征点处层位移和层间位移角。由图15可知,混合联肢PEC墙结构表现出明显的弯曲变形特征,结构的层位移和层间位移角均随高度的增加而增加,最大值均出现在顶层。各特征点处,层位移曲线均在一层出现明显转折,层间位移角曲线则在一层差异最大。观察算例结构层间位移角的分布情况可知,同一状态下,层间位移角差异随楼层数增加而减小,底部三层差异较大;不同状态下,层间位移角差异随结构塑性发展程度提高而增大。

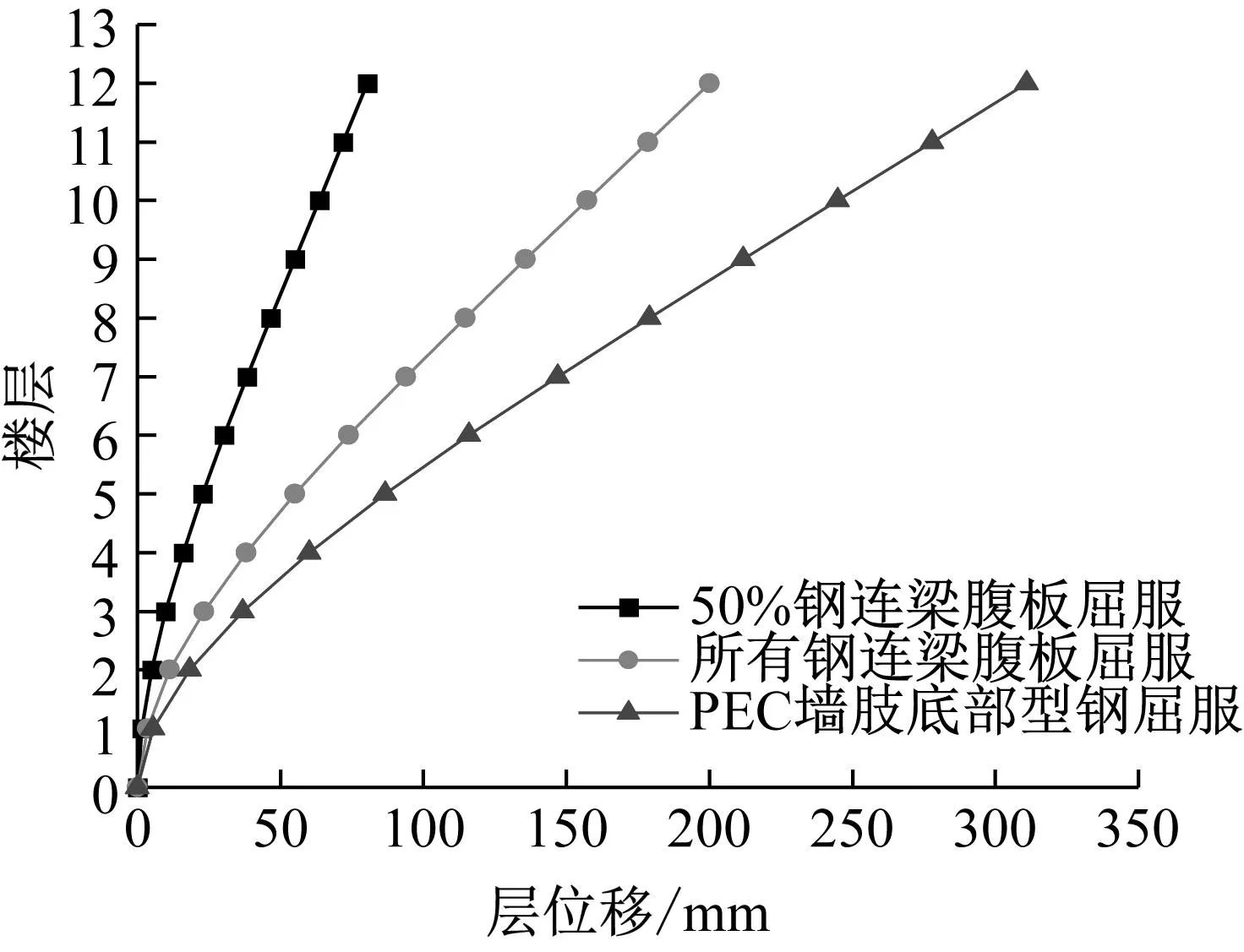
(a) 层位移

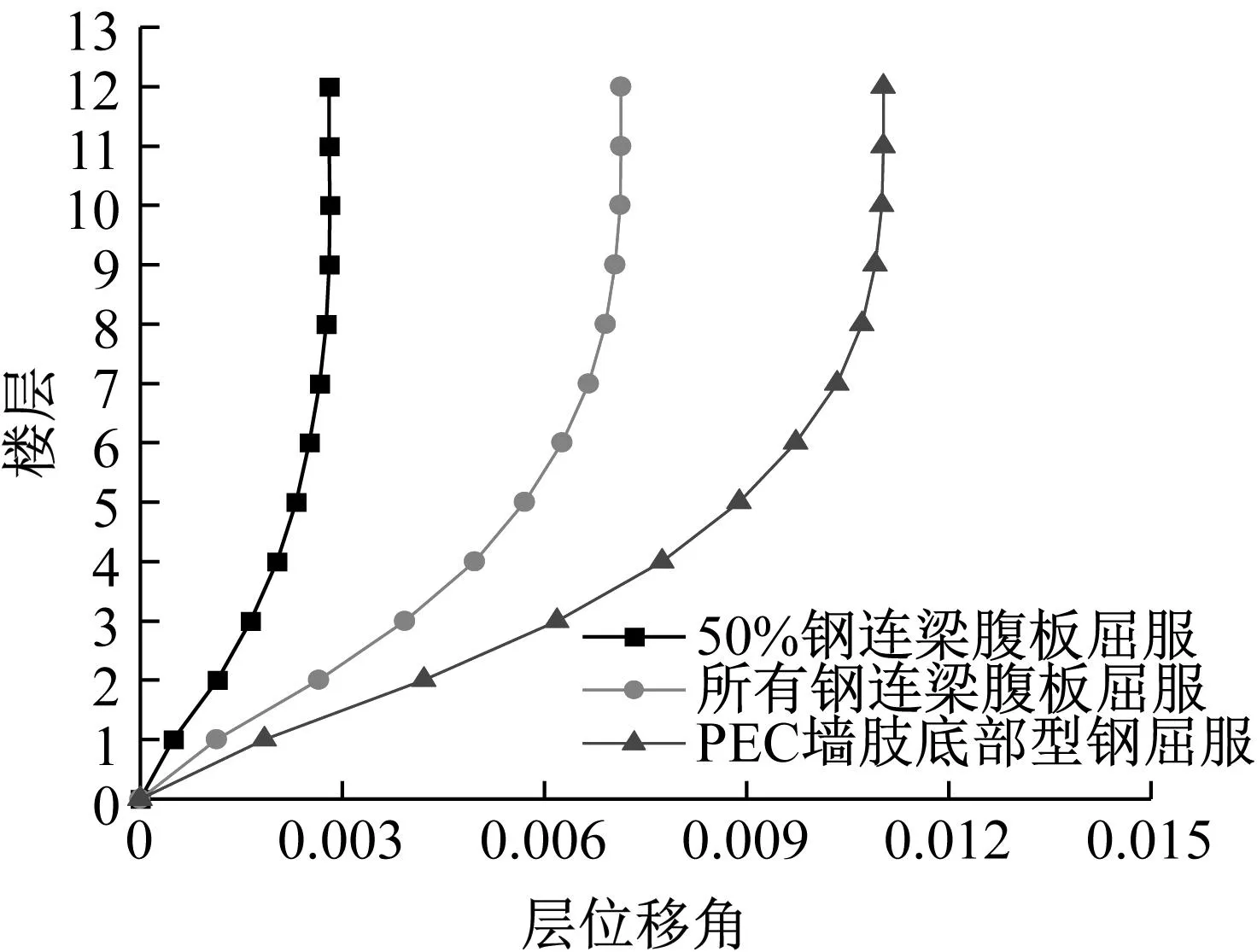
(b) 层间位移角图15 算例结构特征点处层位移和层间位移角Fig.15 Story displacement and inter-story drift ratio at the characteristic points of the model

5.5 时程分析

为对算例结构进行弹塑性动力时程分析,采用基于设计反应谱的选波方法,选取5条天然地震波,并生成2条人工波,共同组成时程分析地震波记录选择集,如表8所示。图16对比了7条地震波调幅后的平均反应谱与目标反应谱,可见二者吻合程度较高,满足我国抗规中“统计意义上相符”的规定,后续将采用该7条地震波作为算例结构弹塑性动力时程分析的地震动输入。

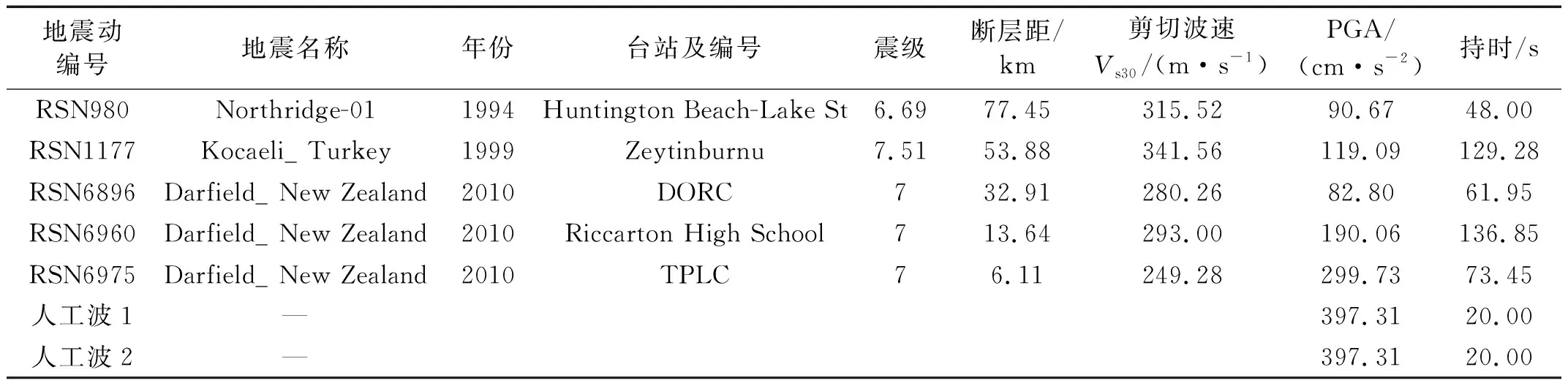
表8 地震波记录选择集Tab.8 Selection set of seismic wave

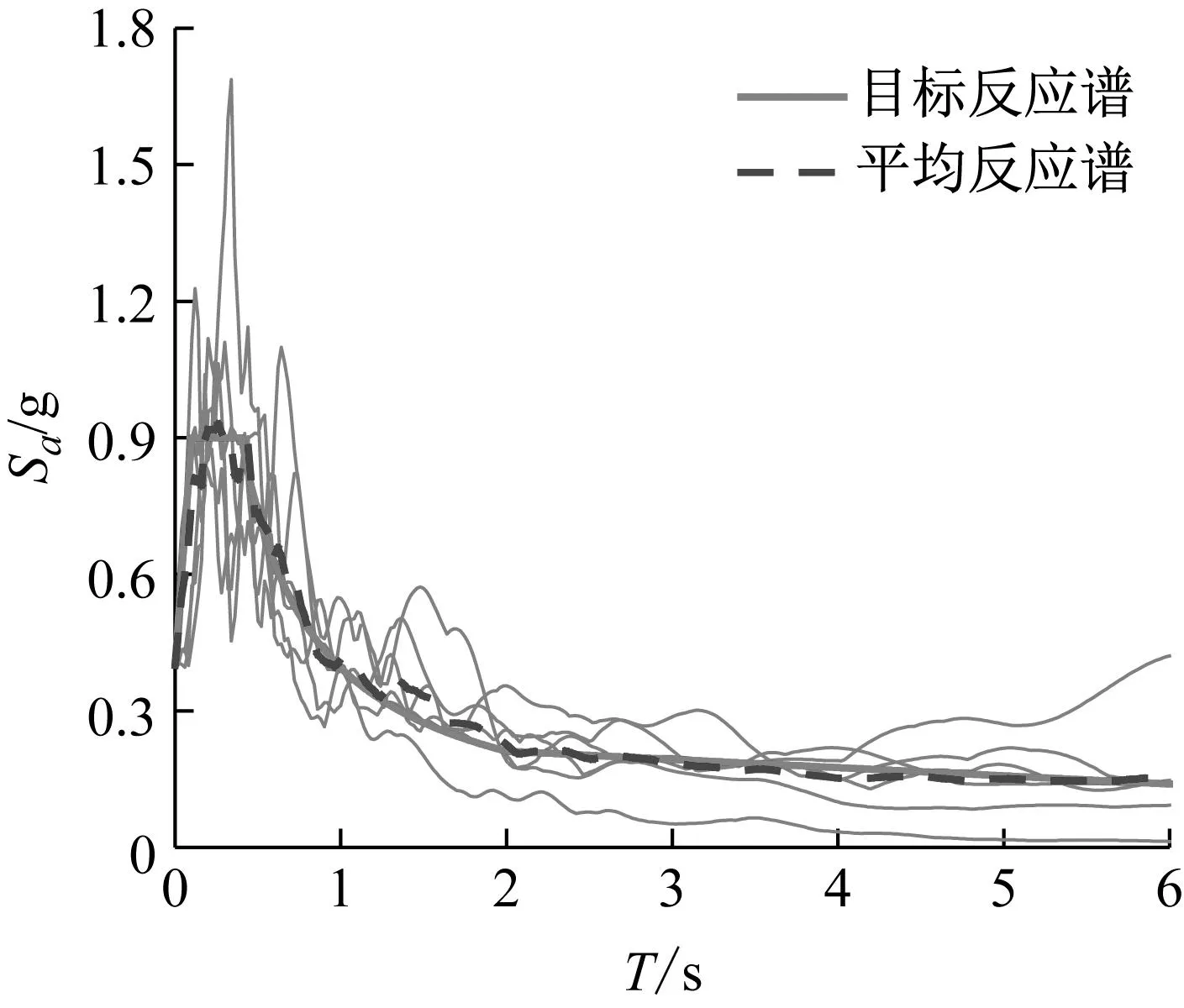
图16 反应谱对比Fig.16 Comparison of response spectrum

(1) 钢连梁剪力

算例结构罕遇地震作用下钢连梁最大剪力及归一化最大剪力分布如图17和图18所示。罕遇地震作用下,各层钢连梁剪力均已超过连梁设计屈服剪力,进入塑性状态。与Pushover分析结果类似,中上部连梁归一化设计剪力分布与七条地震波时程分析结果吻合较好,而底部连梁归一化设计剪力稍大于时程分析结果平均值。总的来说,基于层剪力分布系数βi确定的钢连梁剪力分布模式与混合联肢PEC墙结构中各层钢连梁剪力分布情况基本相符。

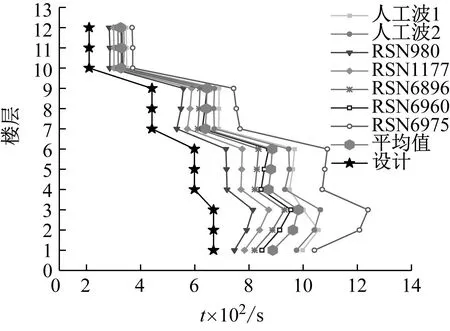
图17 钢连梁最大剪力分布Fig.17 Maximum shear distribution of steel coupling beams

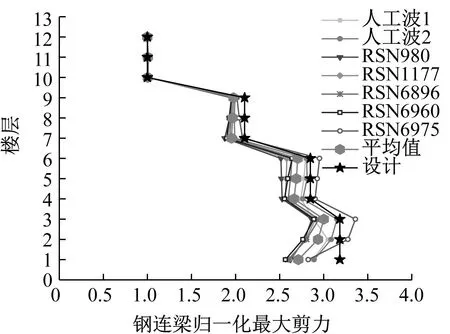
图18 钢连梁归一化最大剪力分布Fig.18 Normalized maximum shear distribution of steel coupling beams

(2) 变形

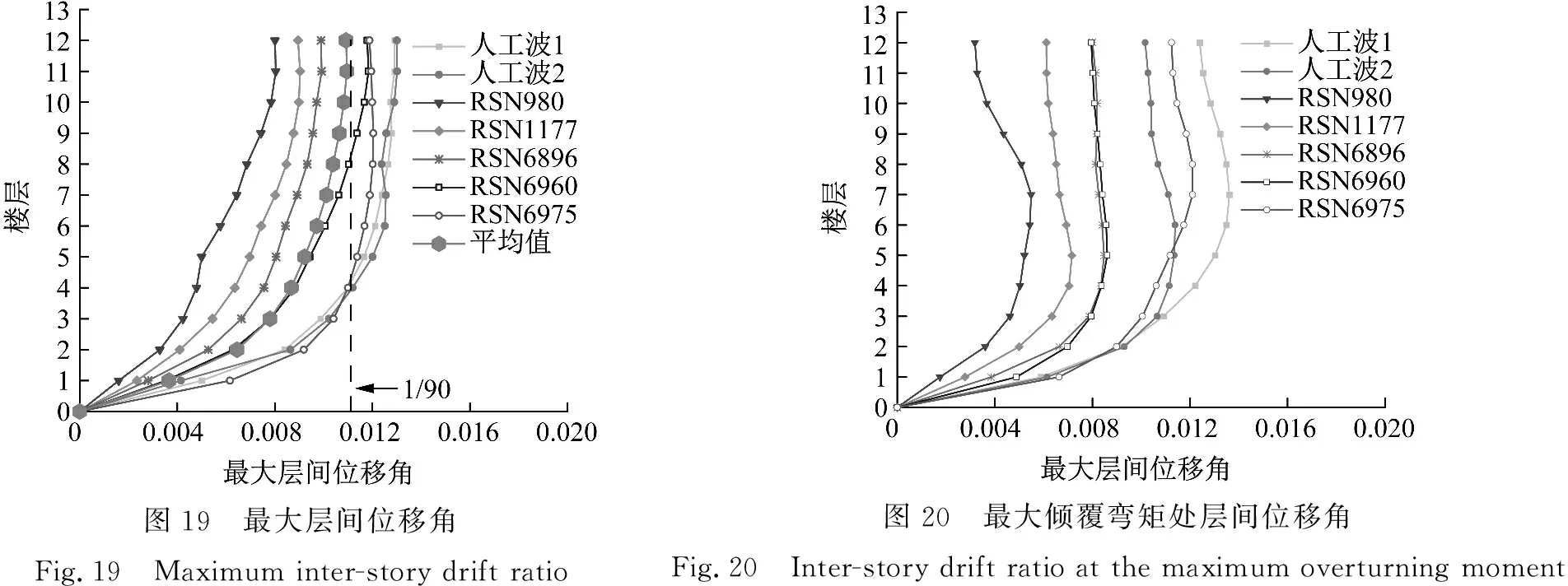
算例结构在罕遇地震作用下的最大层间位移角分布,如图19所示。罕遇地震作用下,结构各层最大层间位移角平均值均小于1/90,满足给定性能目标。图20给出了结构在7条地震波作用下最大倾覆弯矩处层间位移角分布,与Pushover分析结果不同,地震作用下层间位移角最大值出现在结构中部而不是上部,不再表现出明显的弯曲变形特征,表明结构受高阶振型影响显著。

(3) 塑性铰分布

以人工波1为例,给出算例结构钢构件在罕遇地震作用下的Von Mises应力分布,如图21所示。通过钢构件应力是否达屈服强度来判断其是否进入塑性,形成塑性铰。由图可知,算例结构塑性铰集中于各层钢连梁腹板以及PEC墙肢底部,且各层钢连梁腹板全截面进入屈服,塑性发展充分,墙肢则仅在底部形成塑性铰,与预先选定的破坏模式相符,实现了沿墙高布置钢连梁首先剪切屈服耗散能量,然后PEC墙肢底部形成弯曲塑性铰的“两阶段耗能体系”性能目标。

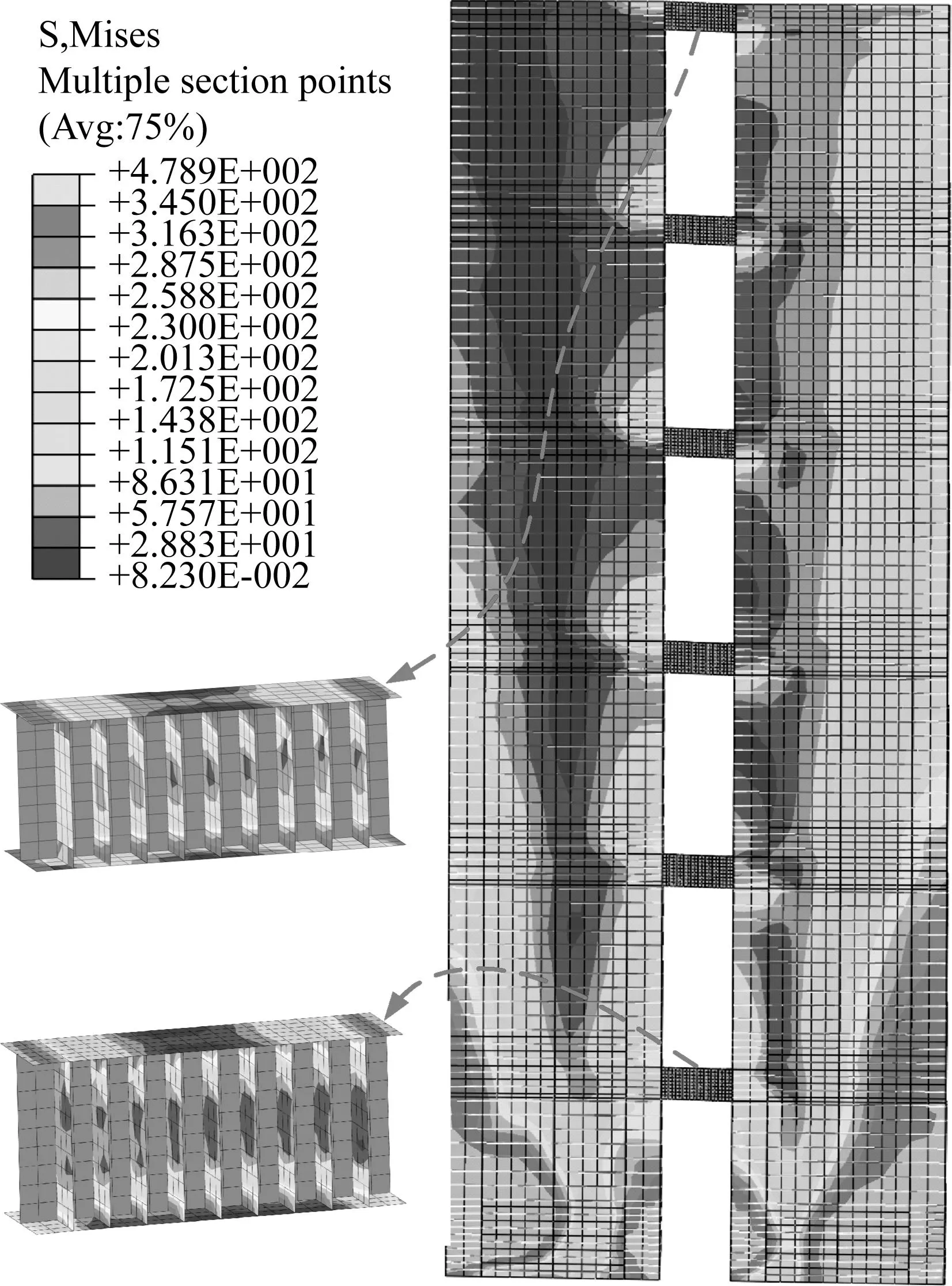
(a) 1～6层钢构件应力分布

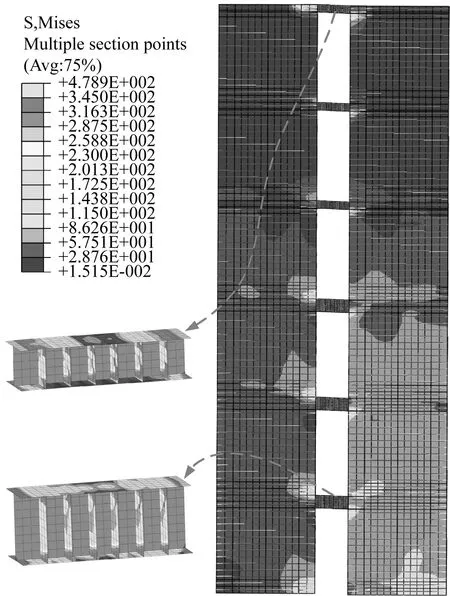
(b) 7～12层钢构件应力分布图21 钢构件Von Mises应力分布Fig.21 Von Mises stress distribution of steel members

6 结 论

基于性能化设计理念,提出混合联肢PEC墙结构基于合理失效模式的性能化设计方法,并给出完整设计流程。在此基础上,为验证基于合理失效模式的性能化设计方法的可行性,设计了12层混合联肢PEC墙结构,并在ABAQUS软件中进行Pushover分析和弹塑性动力时程分析评估其抗震性能。主要结论如下:

(1) 基于合理失效模式的性能化设计方法以结构达目标位移时实现合理的失效模式为性能目标,在结构设计过程中考虑其非弹性性能。采用基于合理失效模式的性能化设计方法设计的混合联肢PEC墙结构,在地震作用下表现出可控的非弹性性能及良好的抗震性能。

(2) 采用的设计基底剪力是基于混合联肢PEC墙结构实现预定的性能目标,达目标位移时实现合理的失效模式,结构处于弹塑性状态计算得到,能够较为准确地控制结构的塑性分布及破坏模式。

(3) 对采用基于合理失效模式的性能化设计方法设计的混合联肢PEC墙结构,进行了Pushover分析和弹塑性动力时程分析,验证了基于合理失效模式的性能化设计方法的可行性。基于合理失效模式的性能化设计方法设计的混合联肢PEC墙结构抗震性能良好,地震作用下,各层钢连梁首先剪切屈服耗散能量,然后PEC墙肢底部形成弯曲塑性铰,塑性铰分布及发展过程符合预期,实现了“两阶段耗能体系”的设计目标。

(4) Pushover分析和弹塑性动力时程分析结果均表明,基于层剪力分布系数βi确定的钢连梁剪力分布模式与混合联肢PEC墙结构中钢连梁剪力分布情况基本相符,可偏于保守的基于层剪力分布系数确定钢连梁剪力需求,然后进行钢连梁截面设计。