基于RBFNN-ISSA的特大跨径悬索桥有限元模型修正

王祺顺, 何 维, 吴 欣, 郭伟奇1,, 雷顺成

(1. 湖南省交通科学研究院有限公司, 交通建设工程湖南省重点实验室, 长沙 410015;2. 长沙理工大学 土木工程学院 桥梁工程安全控制省部共建教育部重点实验室, 长沙 410015;3. 湖南大学 土木工程学院 风工程与桥梁工程湖南省重点实验室, 长沙 410082)

在对现役桥梁结构进行静、动力特性研究时,往往依赖于合理的有限元模型,而基于桥梁设计图纸等资料建立的有限元模型在一定程度上仅能反映桥梁结构在理论上的力学特性。实际上,有限元模型对于真实桥梁结构模拟的精度十分依赖于自身参数的准确性,真实的桥梁结构在环境因素和外界荷载的作用下的结构响应规律并不一定与理论模型十分吻合,因此,为减小有限元模型的模拟误差,在对真实桥梁结构进行荷载试验获取实测数据的基础上,反向修正基于设计资料建立的初始有限元模型,是准确研究桥梁结构力学特性的重要手段。

目前常用的有限元模型修正方法分为两类,一类是以响应面代理模型为核心的有限元模型修正[1],另一类是将有限元模型修正转化为数学优化问题,采用合适的算法进行迭代寻优求解,以上两个方向均有众多专家学者做了深入研究。支持向量机、神经网络、贝叶斯网络和Kriging等模型理论是有限元模型修正时常用的响应面代理模型,王一航等[2]基于Kriging理论建立了某机械结构的有限元模型,通过实测模态频率修正了初始有限元模型的边界参数,保证了理论模型与实际结构动力特性的一致性;卢彭真等[3]针对变截面桥梁有限元模型修正问题提出了基于Kriging代理模型和动载试验的修正方法,根据修正后模型结构响应与实测值的对比验证了该方法的可行性;Wu等[4-5]同样采用Kriging理论对大跨径拱桥有限元模型材料参数的修正进行了研究;Jaishi等[6]提出了基于灵敏度理论,以静、动力特征差异为目标函数对钢管混凝土拱桥有限元进行了模型修正;刘才玮等[7-12]一些专家学者基于支持向量机等机器学习理论提出了有限元模型的快速修正方法,从相关研究结果可知,支持向量机等机器学习算法建立的代理模型可以在保证有限元拟合精度的前提下大幅提升模型修正效率,但仍然存在修正精度不高的问题。

以上研究均验证了响应面代理模型方法在有限元模型修正中的可靠性,随着计算机技术的发展与更新,部分专家学者尝试改进不同类型的智能算法并应用于工程参数的优化求解中[13-16]。唐煜等[17]基于人工蜂群算法对桥梁有限元模型局部刚度进行了修正;付雷等[18]依托桥梁健康监测系统,采用鲸鱼优化算法对桥梁初始有限元模型静动力特性进行了修正;Perera等[19]提出了混合粒子群算法和遗传算法的桥梁模型修正方法;此外,还有一些专家学者也通过不同的智能算法进行了相应的研究[20-22],由相关研究结果可知,目前智能算法在对大型复杂结构的有限元模型修正参数进行修正时,修正精度和效率往往依赖于算法本身的寻优性能,且部分智能算法的适用性问题仍值得进一步考证。

大跨径悬索桥工程规模庞大,结构构件之间的耦合关系复杂,在对该类工程进行有限元模型修正时,常规的修正方法往往不能达到理想的效果,且模型修正的计算成本非常高昂。基于此,为实现大跨径悬索桥结构等大型工程有限元模型的快速准确修正,本文提出一种联合RBF神经网络子结构代理模型与改进麻雀搜索算法的有限元模型参数修正方法。基于子结构理论和RBF神经网络对初始有限元模型进行解构重组和拟合,将有限元模型的参数修正问题转化为静、动力特征计算误差下的参数优化问题。新方法通过Tent混沌映射、黄金正弦收敛和柯西变异混合策略改进了标准麻雀搜索算法,并基于MATLAB平台设计了基于RBF神经网络和改进麻雀搜索算法的高效联合求解流程。在杭瑞高速洞庭湖大桥上进行现场试验,基于实测数据验证了该方法的准确性。结果表明,利用新方法建立了大跨径悬索桥梁的准确有限元模型,并且计算效率和稳定性获得了显著的提高。

1 工程概况及初始有限元模型建立

1.1 工程背景

杭瑞高速洞庭湖大桥为杭州至瑞丽国家高速公路上的一座双塔双跨钢桁梁悬索桥,主跨跨径1 480 m,是目前世界最大跨径的板桁结合型加劲梁悬索桥,系中国第二、湖南省第一大跨径的钢桁梁悬索桥。大桥主缆跨径布置为460 m+1 480 m+491 m,主梁全长1 933.6 m。主桥位于直线上,沿主桥跨中设双向1.5%纵坡,曲率半径为49 000 m,横桥向设2%横坡,桥面系宽33.5 m,加劲梁全宽35.4 m。采用两根主缆,中跨主缆垂跨比为F/L=1/10,主缆中心间距为35.4 m,采用平面索布置。每根主缆中从君山侧锚碇到岳阳侧锚碇的通长索股有175股,君山侧边跨另设6根索股(背索)在君山侧主索鞍上锚固,主缆在架设时竖向排列成尖顶的近似六边形,紧缆后主缆呈圆形。全桥共117对吊杆,吊杆标准间距为16.8 m,跨中吊杆的间距为17.6 m。桥面系采用正交异性钢桥面板,面板厚12 mm,下设U形加劲肋和板式加劲肋。

根据桥梁的实际情况,对桥梁结构进行成桥状态初始检查,进行静力及动力荷载试验。采用有限元软件对理想状态桥梁进行计算分析,根据结构整体及局部最不利受力状态,同时参考设计施工时颁布的相关规范[23],最终确定大桥静载试验的内容,试验加载车辆和试验项目的荷载效率系数满足JTG/T J20-01—2015《公路桥梁荷载试验规程》要求[24-25]。静载试验为98辆满载为40 t的后八轮工程车,通过分级加载形式进行加载,本文选取第一级和第四级两个静载试验工况,P1、P2分别为加载车辆前、后轴轴重,加载效率分别为27%、76%,采用全站仪测量各测点竖向挠度。模态试验基于无线振动测试系统进行模态测试。桥型及实桥测点和车辆加载布置图如图1所示。钢桁架标准横断面如图2所示。荷载试验现场照片如图3所示。

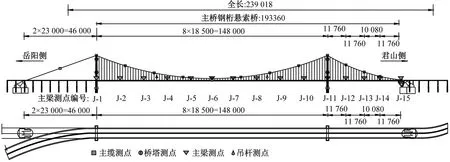
(a) 桥型及测点布置图(cm)

(b) 加载示意图 (kN)图1 测点及加载布置图Fig.1 Layout of measuring points and loading

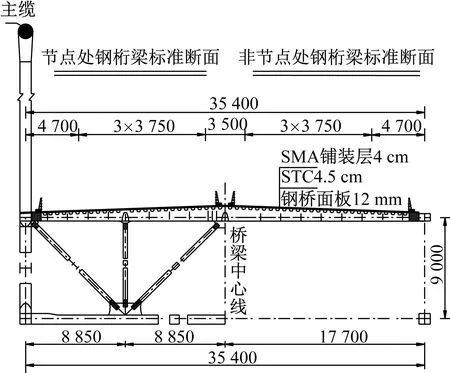
图2 钢桁架标准横断面图(mm)Fig.2 Standard cross section of steel truss (mm)

(a) 现场观测照片

(b) 静载试验图3 荷载试验照片Fig.3 Static load test photos

1.2 初始有限元模型建立

采用大型通用有限元软件ANSYS建立杭瑞高速洞庭湖大桥的初始有限元模型。桥塔、主梁采用BEAM44变截面三维梁单元进行模拟,主缆及吊杆采用LINK10单元进行模拟,桥面铺装等采用MASS21质量单元进行模拟。锚索、桥塔边界采用全固结约束,采用扫掠分网、结构化分网方式对模型进行网格划分。桥梁初始有限元模型主要材料参数如表1所示。有限元模型如图4所示。

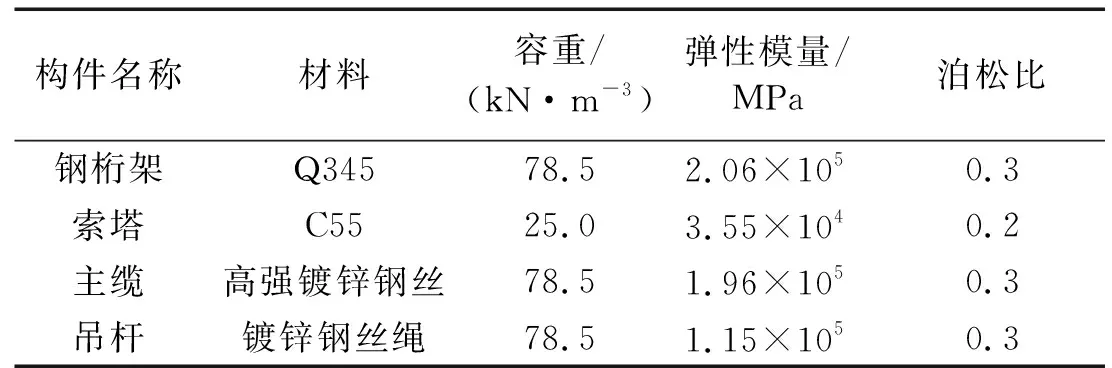
表1 初始有限元模型主要材料参数Tab.1 Initial finite element model material parameters

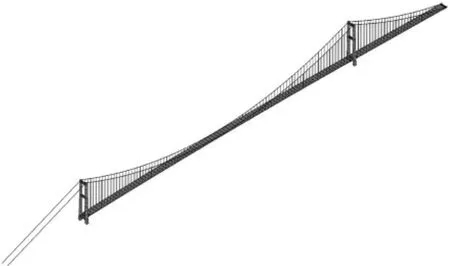
图4 桥梁初始有限元模型Fig.4 Original finite element model of the bridge

2 RBFNN子结构代理模型

2.1 RBF神经网络

在对悬索桥模型进行参数修正时,应采用恰当的结构代理模型作为迭代计算模型进行优化分析,径向基神经网络(radial basis function neural network, RBFNN)是一种前馈型神经网络,基于聚类算法的径向基神经网络能够快速获取隐含层节点,对于结构非线性映射关系的拟合具有良好的适应性,故本文采用聚类算法径向基神经网络建立大跨径悬索桥的结构代理模型。

RBFNN的标准结构为三层,分别为表示设计变量的输入层、表示目标变量的输出层和以径向基函数作为激活函数的隐含层。与其他人工神经网络采取全局逼近的方式不同,径向基神经网络是一种局部逼近神经网络,隐含层到输出层采用线性权进行映射,学习泛化速度快,其网络结构如图5所示。

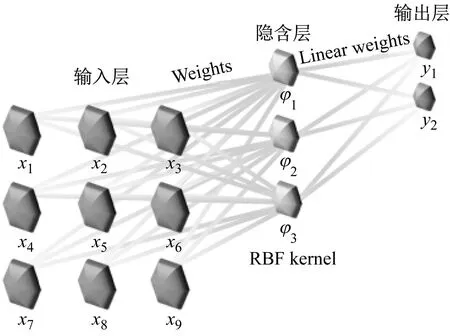
图5 三层径向基神经网络结构示意Fig.5 Radial basis function neural network structure

以悬索桥关键设计材料参数为输入层设计变量,桥梁在荷载效应下的结构响应作为输出层目标变量,隐含层采用高斯径向基函数建立设计变量与目标变量之间的非线性映射关系,高斯径向基函数的表达形式如式(1)所示

(1)

式中,σ为径向基函数的均方差。

2.2 子结构代理模型

由于悬索桥结构工程较为复杂,将悬索桥整体结构作为有限元模型修正的基本单元时,设计变量较多,迭代计算量较大,因此本文采用子结构法建立悬索桥的有限元修正代理模型[26]。子结构方法将悬索桥整体划分为若干子结构单元,通过不同子结构单元上的位移协调条件和力平衡条件进行组合,得到整体结构特性的过程。基于子结构缩聚简化理论建立的特征方程如式(2)所示

(2)

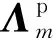
通过子结构方法对大跨度悬索桥整体模型进行解构重组,可以在保证有限元模型计算精度的基础上大幅提升修正阶段的模型迭代效率,降低优化计算成本。

3 改进麻雀搜索算法

3.1 标准麻雀搜索算法

结构有限元模型修正过程实质上可以描述为数学优化模型,并进行优化求解。为提高有限元模型修正的精度与效率,本文提出一种改进的麻雀搜索算法对数学优化问题进行寻优计算。

标准麻雀搜索算法通过模仿麻雀觅食与反捕食的社会性行为实现种群整体向搜索空间中最优位置迁徙[27-30],定义麻雀种群中负责觅食的群体为探索者,其在d维搜索空间的位置更新公式如式(3)所示

(3)

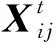
定义麻雀中适应度值较低的个体为追随者,追随者根据探索者的位置更新自己的位置,其位置更新公式如式(4)所示

(4)

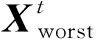
定义搜索空间中存在安全区域,麻雀种群中一定数量个体受到天敌威胁,按适应度值对其位置进行扰动,受威胁麻雀个体的位置更新扰动如式(5)所示

(5)

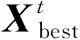
3.2 融合混沌映射和柯西扰动的改进策略

标准麻雀搜索算法相较于其他同类智能优化算法,对高维优化问题具有一定的适应性,但在实际工程中,仍然存在收敛速度慢,寻优鲁棒性不足等问题。为改善麻雀搜索算法的寻优性能,使其适应RBF神经网络子结构有限元代理模型的参数修正问题,提出一种混合策略改进的麻雀搜索算法(improved sparrow search algorithm, ISSA),首先在初始化阶段放弃随机初始化种群策略,引入一种Tent混沌映射策略进行初始化种群操作,其次针对原探索者的自然常数指数型位置更新策略进行改进,引入基于黄金正弦分割的位置更新策略进行位置更新,最后采用柯西函数对麻雀种群进行变异扰动,保留最优个体。

Tent混沌映射又称帐篷映射,相较于确定性系统分析,Tent混沌映射在系统中具有较为均匀的分布函数和良好的相关性[31]。对于初始化种群策略而言,非线性的混沌系统具有天然的优势,可以使种群在搜索空间中具有更加广阔的遍历性,提高对最优解的收敛速度,避免种群陷入局部最优的情况。混沌映射定义如式(6)所示

(6)

式中,α为Tent混沌映射参数。

取α=0.499,图6给出了Tent混沌映射在5 000维度内的分布情况。从图6可以看出,Tent混沌值位于0～1之间,分布均匀。图7给出了混沌值分布的频数范围。从图7可以看出,[0,1]区间内各阶段混沌值频数基本分布均匀,效果显著。

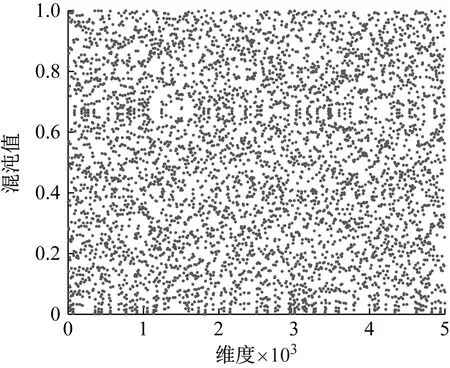
图6 Tent混沌映射分布Fig.6 Tent chaotic map distribution

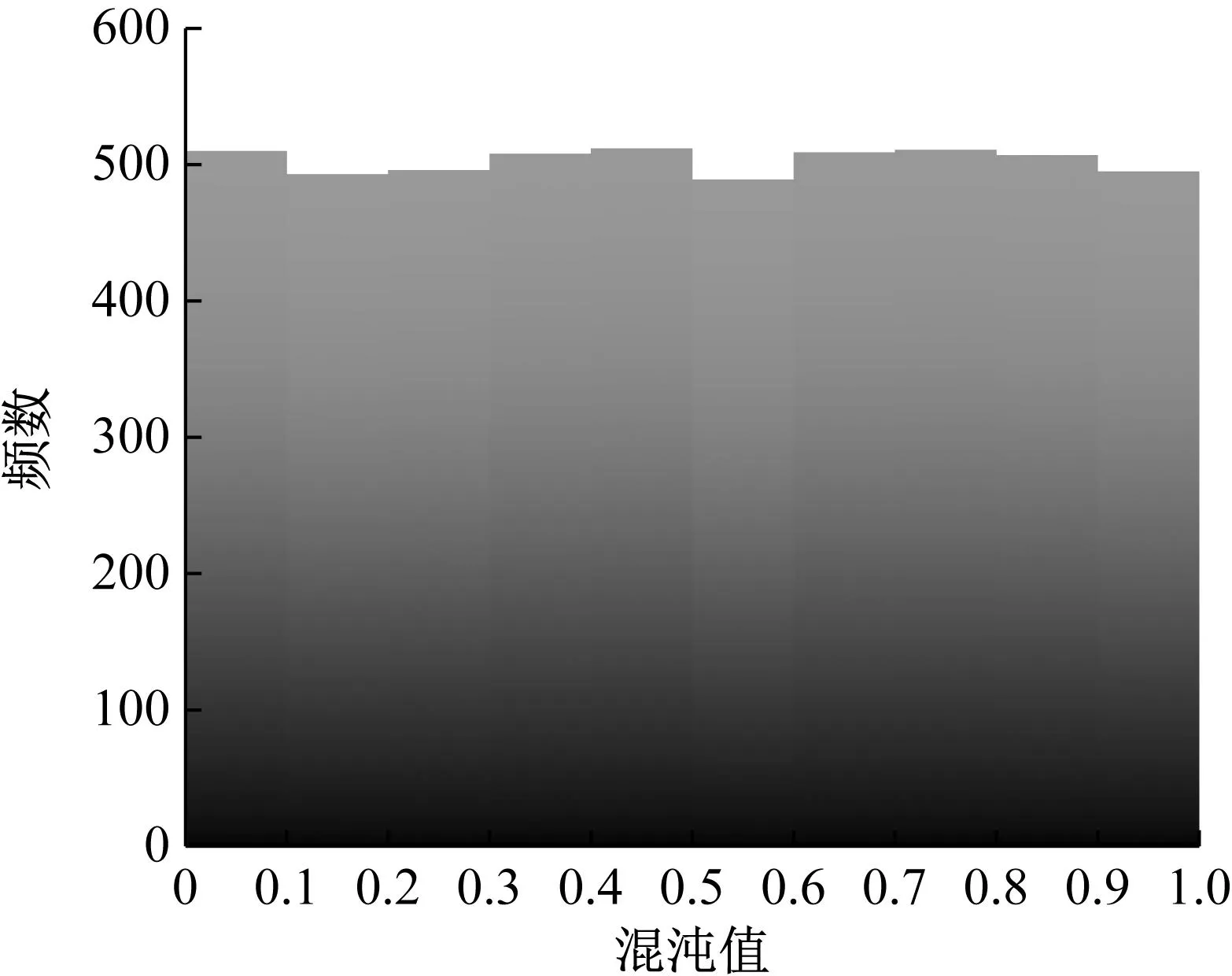
图7 Tent混沌值分布区间(样本总数: 5 000)Fig.7 Tent chaos value distribution interval(total number of samples: 5 000)

黄金正弦算法是一种基于正弦函数的迭代寻优的计算方法[32],为平衡麻雀种群有限元模型参数寻优过程中全局搜索和局部开发偏好的平衡,引入黄金分割比改进探索者的位置更新过程,改进后的探索者位置更新策略如式(7)所示

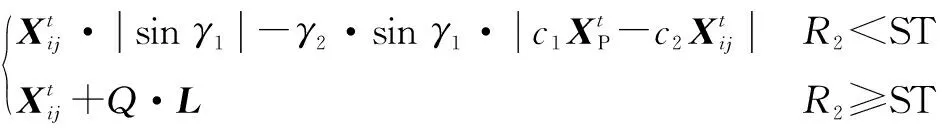
(7)

(8)

式中:γ1为[0,2π]上的随机数;γ2为[0,π]上的随机数;c1、c2为黄金分割系数;g为黄金分割参数。

对于有限元模型修正的数学优化问题,同一个模型参数在不同取值区间段的均可能达到令模型误差减小的效果,在麻雀搜索算法中则表征为麻雀个体在搜索空间中存在多个处于相邻位置的局部极值。为提升麻雀种群的鲁棒性,本文提出一种基于柯西分布的扰动函数对受威胁个体进行位置变异操作,见式(9)

(9)

式中:Cauchy为标准柯西分布函数,其表达式为Cauchy(x)=1/[π(1+x2)];σ2为柯西分布标准差;fC为基于柯西扰动的新麻雀个体适应度值。

图8给出了标准正态分布和标准柯西分布的函数图像。从图8可以看出,相较于标准正态分布,柯西函数的分布范围更加宽泛。采用柯西函数对麻雀个体进行变异扰动后,对新个体采取贪心保留策略,即保留变异后适应度较高的个体,舍弃变异后适应度较低的个体,以保证麻雀种群向搜索空间中的最优区域逼近。

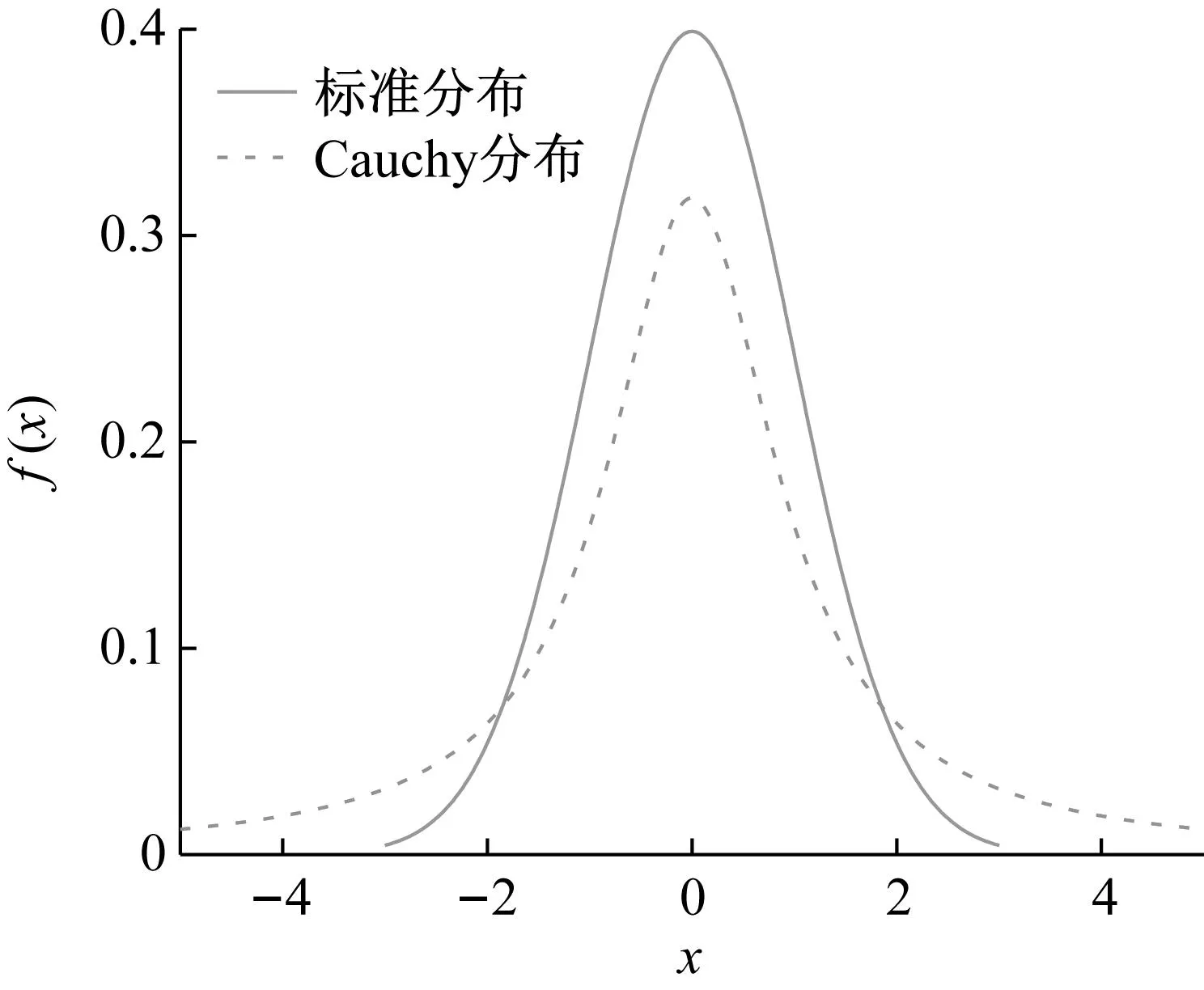
图8 Cauchy分布函数Fig.8 Cauchy distribution function

3.3 基准函数测试

如表2所示,采用4个不定维基准测试函数对混合改进策略改进的麻雀搜索算法(ISSA)进行收敛能力测试[33]。同时,引入标准麻雀搜索算法(SSA),标准粒子群算法(PSO)横向对比算法性能,所有算法种群规模均取40,最大迭代次数为500次,函数维度设置为20,算法基本参数如表3所示。

表2 测试函数信息Tab.2 Test function information

表3 算法参数设置Tab.3 Algorithm parameter settings

各算法独立运行30次,采用平均值(AVG)、最优值(BEST)和标准差(STD)衡量各算法的寻优精度及稳定性,表4给出了各算法在不同测试函数下的寻优结果。从表4可以看出,对于单峰测试函数F1,PSO、SSA和ISSA算法所有种群个体均能收敛至理论全局最优。对于多峰测试函数F2、F3和F4,PSO算法和SSA算法的寻优结果没有形成明显的差距,但ISSA在多峰测试函数F2、F3和F4中表现出了较高的收敛精度和寻优稳定性,30次算法的平均值、最优值和标准差均为测试算法中最优秀的水平。从算法性能测试的结果可以看出,ISSA对于多峰测试函数局部极值的逃逸能力更强,整体寻优效率更高,混合改进策略的引入大幅提升了麻雀搜索算法的寻优能力和鲁棒性,ISSA相较于标准算法和同类算法在复杂问题的处理上更具优势。

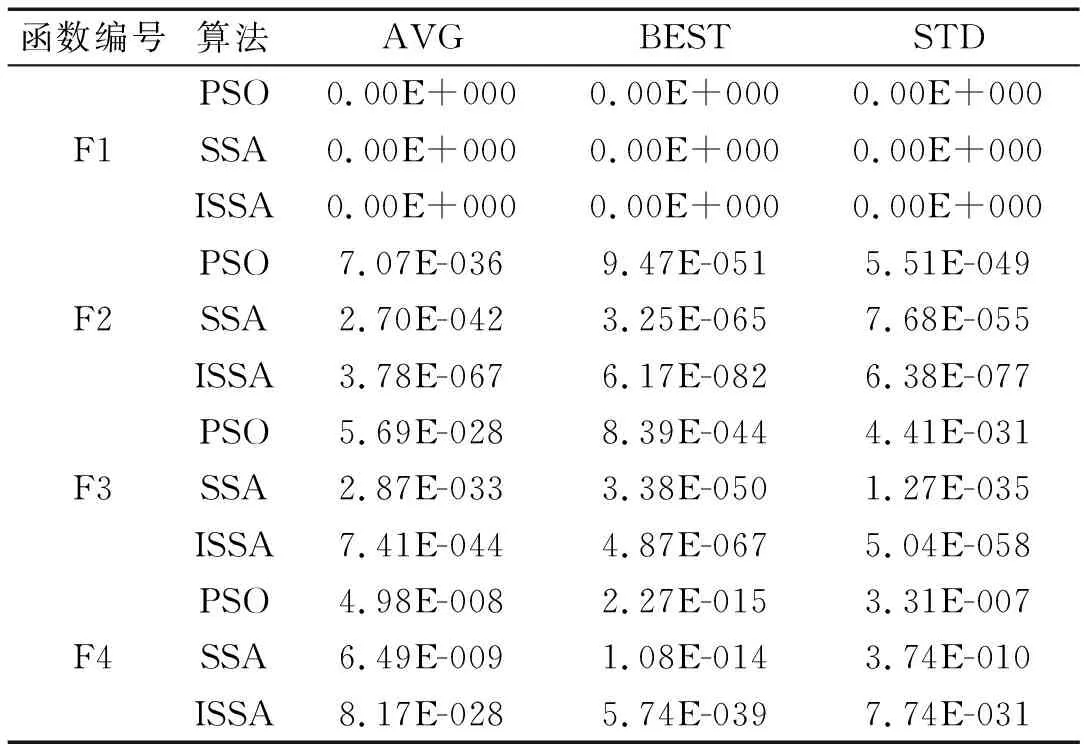
表4 算法性能测试表Tab.4 Algorithm Performance Test Table

4 基于RBFNN-ISSA算法的有限元模型修正

基于RBFNN子结构模型和ISSA算法的有限元模型修正流程如下:

(1) 确定子结构模型划分。根据RBFNN子结构映射模型与提出的ISSA算法,对大跨径悬索桥有限元模型参数进行修正研究。首先,确定大跨径悬索桥的RBFNN子结构模型,根据大跨径悬索桥的结构特性以及材料分布特征,将全桥划分为4个子结构模型,如表5所示。

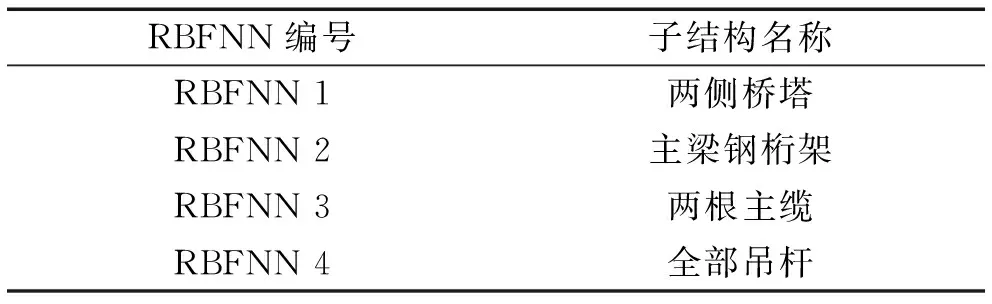
表5 全桥子结构划分Tab.5 Division of Substructure of the whole bridge

(2) 确定设计变量。选取桥塔、主梁、弹性模量变量进行灵敏度分析,采用式(10)计算各变量对结构静、动力响应的灵敏度[34-35]。

(10)

式中:SSEN为修正参数对结构响应的灵敏度;Δv为主梁挠度响应在待修正参数变化后的改变量;v为主梁挠度响应值;Δφ为一阶特征值在待修正参数改变后的改变量;φ为一阶特征值;Δp为待修正参数的摄动量;p为待修正参数的初始值;λ1、λ2分别为静、动力灵敏度的权重,本文综合考虑材料参数对静、动力响应的影响,取λ1=λ2=0.5。

选取各子结构弹性模量和质量密度进行灵敏度分析,表6给出了各待修正变量灵敏度分析结果。由表6可知,各待修正参数对悬索桥结构响应均存在不同程度的影响,其中主梁的材料参数对桥梁结构响应的影响最大。为有效提升结构有限元模型修正的精度,选取各子结构模型的弹性模量和质量密度作为设计变量。考虑到ISSA算法在对有限元模型参数进行修正时应符合参数的实际取值情况,故设计变量的约束条件设计为初始材料参数0.8倍～1.2倍取值区间,设计变量初值见表1。

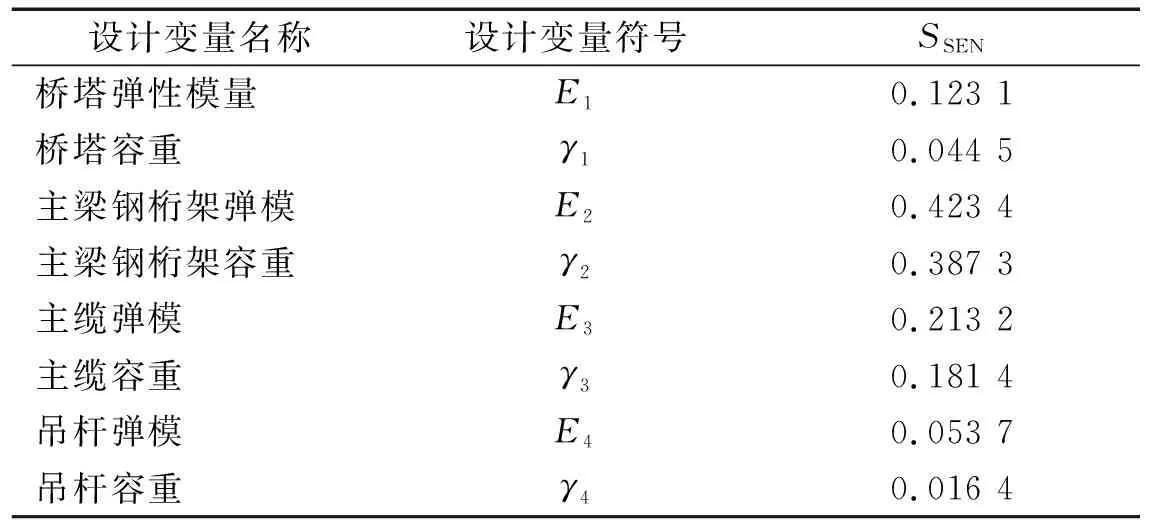
表6 待修正变量灵敏度分析结果Tab.6 Sensitivity analysis results of variables to be corrected

(3) 确定RBF神经网络结构,基于有限元模型计算结果建立材料设计变量与结构响应变量之间的非线性映射关系,采用残差平方和(sum of squares for error, SSE)和复相关系数的平方(R2)检验RBF神经网络对初始有限元模型的拟合精度,SSE越接近0、R2越接近1表示模型拟合精度越高,若R2>0.97则认为RBF神经网络的训练精度满足参数修正的基本要求。SSE和R2计算分别如式(11)、式(12)所示

(11)

(12)

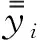
(4) 构建大跨度悬索桥有限元模型修正的数学优化模型。有限元模型修正问题是多约束条件下的最优化问题,根据大跨度悬索桥的实测数据,以修正后的有限元模型结构响应和悬索桥结构实测结构响应一致为优化目标,考虑有限元模型的静、动力特性响应结果,建立结构静、动力特征联合优化目标函数如式(13)所示

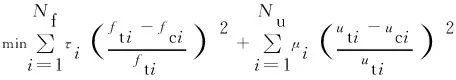
(13)

式中:F(x)为联合静、动力特征目标函数;Nf和Nu分别为频率以及静力位移特征点的数量;fti和fci分别为模型预测频率和结构实测频率;uti和uci分别为模型预测静力位移和结构实测静力位移;τi、μi分别为动、静力误差的权重系数。

为减小测量误差对目标函数的影响,本文采用测量变异系数加权的方法确定动、静力误差权重系数,对测量误差较大的项给予较小的权重系数,对测量误差较小的项给予较大的权重系数,如式(14)所示[36]

(14)

式中,CVτ、CVμ分别为动、静力特征实测值变异系数。

(5) 基于ISSA的最优参数求解。将待修正的设计变量编译为ISSA算法的位置向量,麻雀个体在搜索空间中的位置代表一组设计向量的解集,基于大跨径悬索桥结构静、动力响应的实测结果,通过目标函数值表征麻雀在搜索空间中的适应情况,根据麻雀种群的寻优结果反向编译待修正设计变量的优化结果。

(6) 验证有限元模型修正结果。根据ISSA算法对设计变量的寻优结果对初始有限元模型(Fbefore)进行参数修正,得到优化后的有限元模型(Fafter)。对优化后的有限元模型进行静力及动力计算,与结构荷载试验的实测结果进行对比分析,验证有限元模型修正的效果。采用MATLAB平台建立基于ISSA算法的参数修正流程如图9所示。

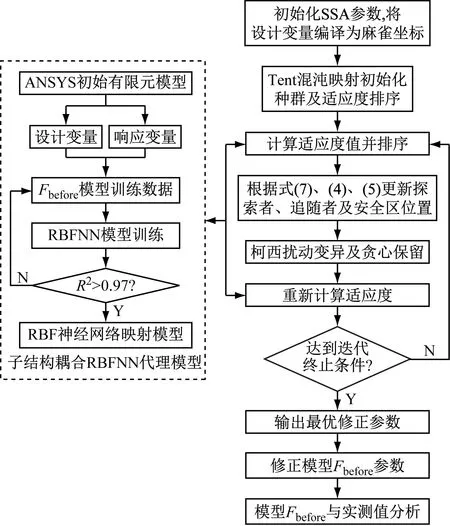
图9 基于ISSA的有限元模型修正流程Fig.9 Finite element model revision process based on ISSA

5 结果验证与分析

根据拉丁超立方设计原则,基于初始ANSYS有限元模型生成悬索桥在荷载作用下的设计变量-结构响应的训练样本与验证样本[37],结构响应选取成桥线形及前八阶模态频率,为避免不同变量单位的影响,对所有变量采取归一化处理,归一化区间取(0,0.1),RBFNN密度常数spread取1.2,采用MATLAB 2018b建立基于子结构联合的RBFNN代理模型,图10给出了50个检验点下的拟合情况。从图10可以看出,50个检验点下的RBFNN网络输出与原有限元模型计算结果拟合效果良好,残差平方和SSE仅为5.11×10-4,复相关系数平方R2为0.979 4,可见训练得到的RBFNN可作为初始有限元模型的代理模型进行模型修正。

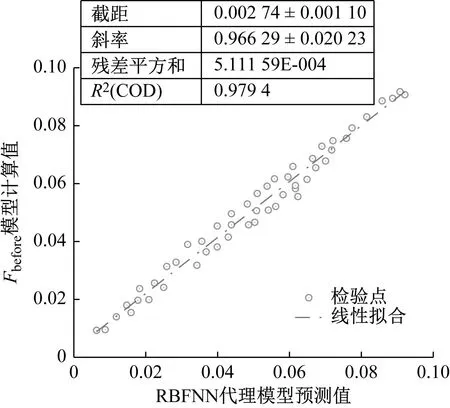
图10 子结构RBFNN拟合精度Fig.10 Substructure RBFNN fitting accuracy

为验证基于子结构耦合的RBFNN代理模型对特大跨径悬索桥工程结构特性模拟的准确性,引入支持向量机、Kriging模型对同一批训练样本进行训练拟合,随机抽取10个验证点,采用不同机器学习模型检验第一阶模态频率与主梁挠度的预测精度,图11给出了10个验证点处各机器学习模型的拟合结果。从图11可以看出,基于子结构耦合的RBFNN模型无论是动力还是静力特征预测结果明显更逼近有限元模型理论值,图中坐标均匀分布在有限元理论计算值附近,而标准RBFNN模型、SVM模型和Kriging模型均与有限元计算结果存在一定偏差,且其他标准模型的预测稳定性较差。图12给出了不同机器学习模型10个检验点的平均相对误差结果。从图12可以看出,基于子结构耦合的RBFNN模型预测精度最高,静、动力特征指标的平均相对误差约为2%,而其他三种机器学习模型预测精度大致相同,Kriging模型预测精度略高于整体RBFNN和SVM。

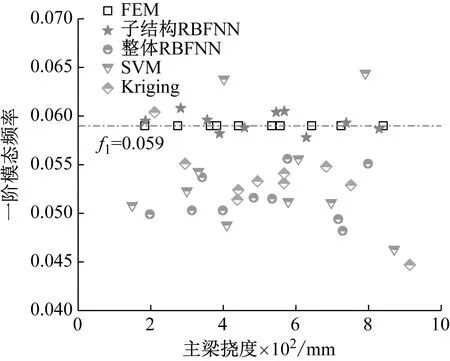
图11 不同机器学习模型预测结果Fig.11 Prediction results of different machine learning models

为验证融合Tent混沌映射和黄金正弦分割改进的麻雀搜索算法对悬索桥有限元模型修正优化问题的有效性,引入标准麻雀搜索算法进行对比分析。设置Tent混沌映射调整参数α为0.499,麻雀种群规模40,最大迭代次数Tmax为300,根据设计变量个数设定麻雀个体维度d为8,探索者初始比例为20%,受威胁的麻雀群体比例为20%,安全阈值ST为0.8。图13给出了标准SSA和ISSA 300次迭代的适应度变化曲线,对比图13最佳适应度曲线可以看出,ISSA的Tent混沌映射策略使得在迭代初期已有部分麻雀个体映射至全局最优解附近,初始最佳适应度值相较于SSA算法更优,从最佳适应度的收敛速率可以看出,ISSA与SSA的收敛速度大致相同,但是SSA算法在第56代左右出现算法收敛停滞的情况,而ISSA算法在第35代即有部分个体收敛至全局最优解。对比平均适应度曲线可以看出,ISSA算法收敛速度远高于SSA算法,且90代左右全体种群基本收敛至全局最优解。SSA算法虽然前期的寻优效率保持在较高的水平,但算法中后期对于局部极值的摆脱能力欠佳,于第160代陷入局部最优解,停止进化后 SSA平均适应度曲线与最佳适应度曲线间仍存在一定差距,证明种群中存在部分个体未收敛至当前的最佳适应度区域。

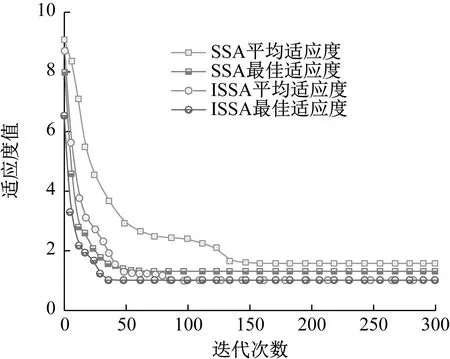
图13 麻雀搜索算法适应度曲线Fig.13 Fitness curve of sparrow search algorithm

反编译ISSA算法输出的最优解集各维度参数,得到修正后的设计变量如表7所示。从表7可以看出,RBFNN-ISSA模型修正后的材料参数与修正前大致相同,但对不同材料的修正方向存在一定的区别,对于混凝土材料的桥塔,修正后的弹性模量及容重均存在小幅度的降低,而对于主梁钢桁架、主缆及吊杆,弹性模量和容重均存在小幅的增加,其中钢结构的弹性模量均增加2%以上,容重增加幅度均小于1%。

表7 设计变量修正结果Tab.7 Design variable correction results

将修正后的材料参数输入原始有限元模型Fbefore,得到修正的有限元模型Fafter。分别计算模型Fbefore和模型Fafter在成桥状态下的结构响应,并与荷载试验实测结果进行对比分析。

由于J1、J15号测点位于大桥两侧支点位置,主梁竖向挠度数值不具备可参考性,故对主梁J2～J14号测点进行静力特征分析。图14(a)、图15(a)分别给出了修正前后钢桁架主梁在第一级(27%加载效率)、第四级静载工况(76%加载效率)下13个有效测点的竖向挠度对比,从图14(a)、图15(a)可以看出,修正前后有限元模型的理论计算挠度与实测挠度趋势大致相同,主跨跨中位置J6测点钢桁架竖向挠度达到峰值,君山侧桥塔处J11测点挠度趋于0,其余各测点挠度分布规律与加载车辆布置相关,第一级加载由于车辆荷载主要集中在跨中位置,故挠度曲线出现明显的陡峰,第四级加载时车辆荷载的作用区间更大,故挠度曲线峰值区域分布范围也较第一级加载更广。从有限元模型计算的理论值分析,修正前的有限元模型钢桁架主梁的挠度计算结果与实测值之间存在较大的偏差,修正后的有限元模型理论计算挠度与实测值拟合程度较高。图14(b)、图15(b)给出了主梁各测点修正前后有限元模型理论计算值与实测值之间的相对误差结果,由图14(b)分析可知,第一级加载工况下,修正前模型13个有效挠度测点的平均相对误差为30.99%,最大相对误差为49.67%(J2测点)。修正后模型13个有效挠度测点的平均相对误差为5.74%,最大相对误差为7.39%(J6测点)。由图15(b)分析可知,第四级加载工况下,修正前模型13个有效挠度测点的平均相对误差为33.48%,最大相对误差为56.22%(J2测点)。修正后模型13个有效挠度测点的平均相对误差为5.92%,最大相对误差为7.87%(J10测点)。

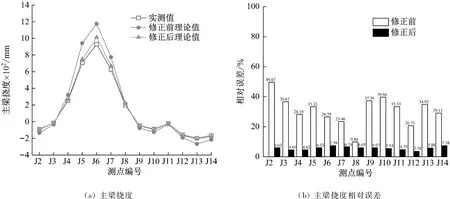
图14 第一级静载试验主梁挠度Fig.14 First level static load test main beam deflection

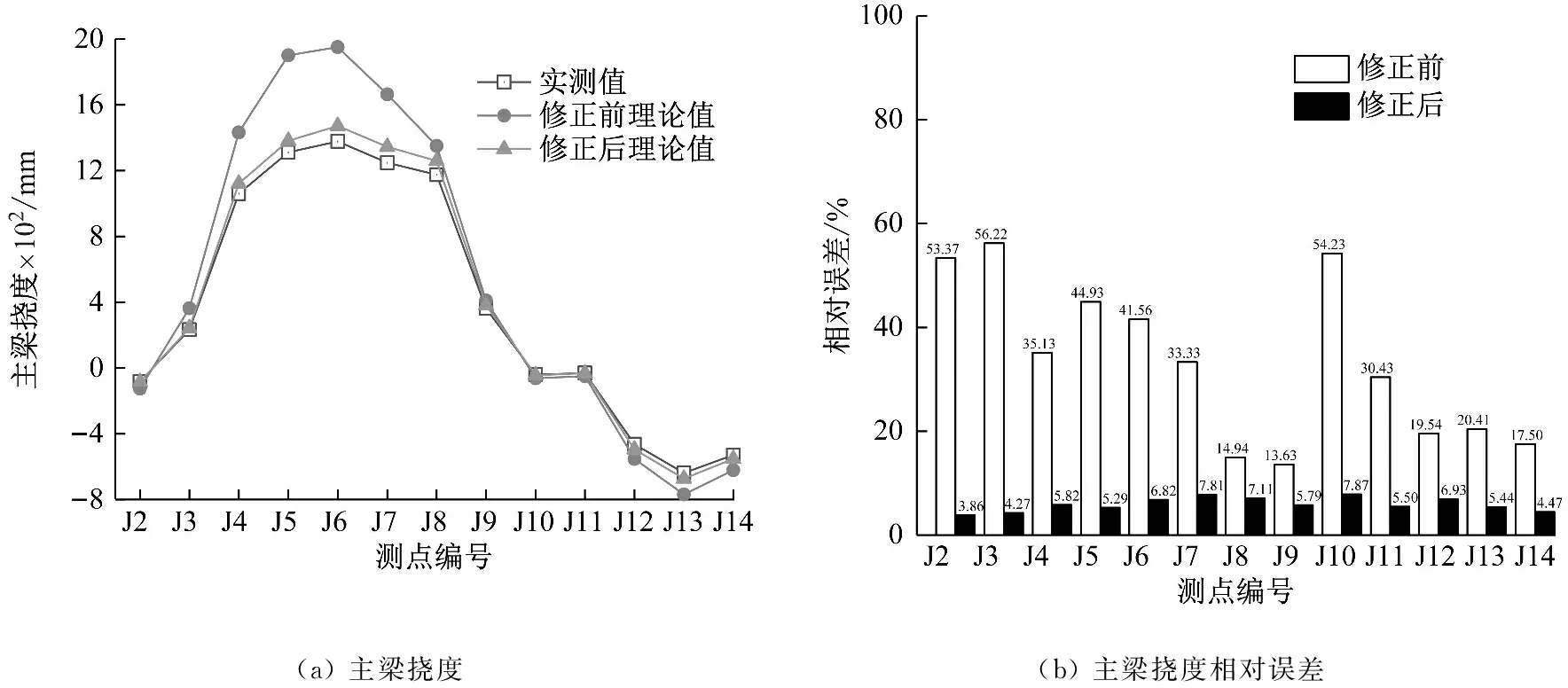
图15 第四级静载试验主梁挠度Fig.15 Fourth level static load test main beam deflection

从各有效测点修正前后有限元模型挠度理论计算值与实测值之间的相对误差结果可知,修正前有限元模型理论计算值与静载试验实测值出入过大,在实际工程中该模型已不具备可参考性。而修正后的有限元模型对悬索桥在静力工况下的钢桁架主梁竖向挠度具有较高的计算精度,更能反映桥梁在静力荷载下的实际受力特性。

表8给出了修正前后模型的前8阶频率计算结果。从表8可以看出,修正前有限元模型对于大跨径悬索桥前4阶动力特性的模拟存在较大的失真,而对于5～8阶模态频率的模拟精度尚可,修正前的前4阶模态频率平均相对误差达到12.17%。修正后的有限元模型明显改善了前4阶的动力特性模拟精度,修正后前4阶模态频率相对误差仅为3.61%。观察第7、8阶模态频率计算结果可知,修正后模型相较于修正前模型对于高阶模态的计算精度存在小幅降低,但仍保持了较高的模拟精度。

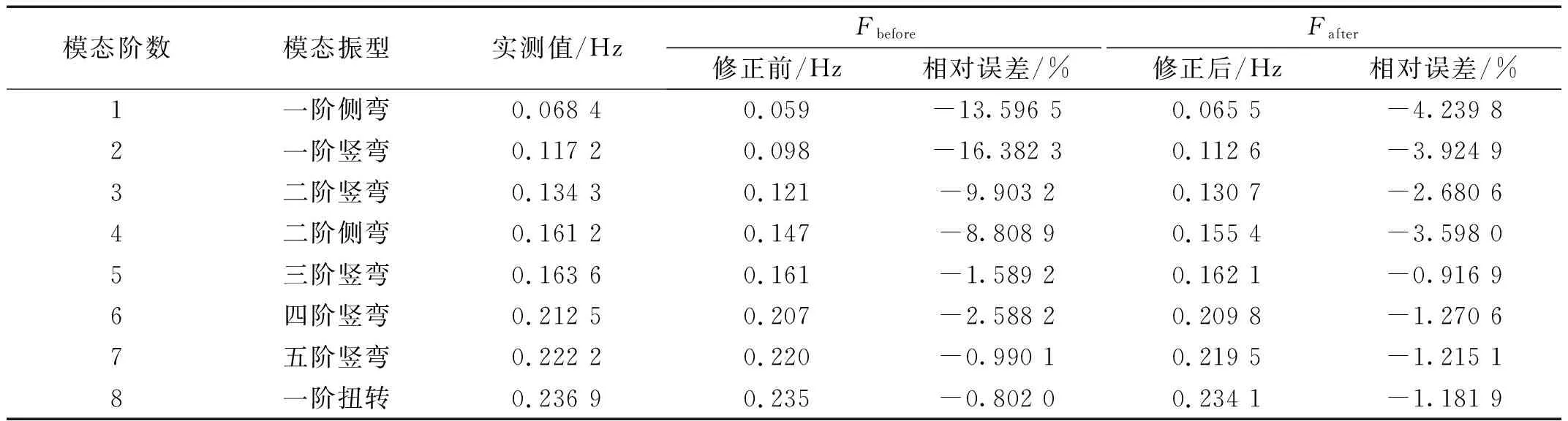
表8 修正前后模态分析结果Tab.8 Modal analysis results before and after correction

为验证修正后的有限元模型与实测振型的匹配情况,采用模态置信准则MAC检查两阶模态之间的相互独立性和一致性。图16给出了前八阶模态理论振动与实测振动MAC值分布。从图16可以得知,前八阶模态MAC值均大于0.9,证明修正后的有限元模型能够较好地逼近杭瑞高速洞庭湖大桥的真实情况,可以准确地反映出大桥的实际振动状态。

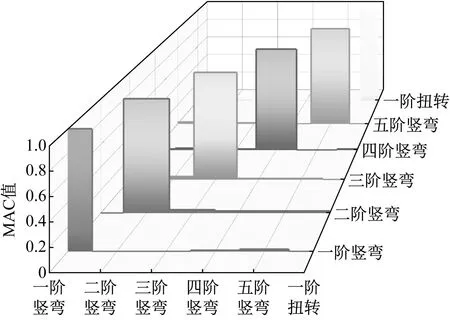
(a) 前八阶竖向模态MAC值图形

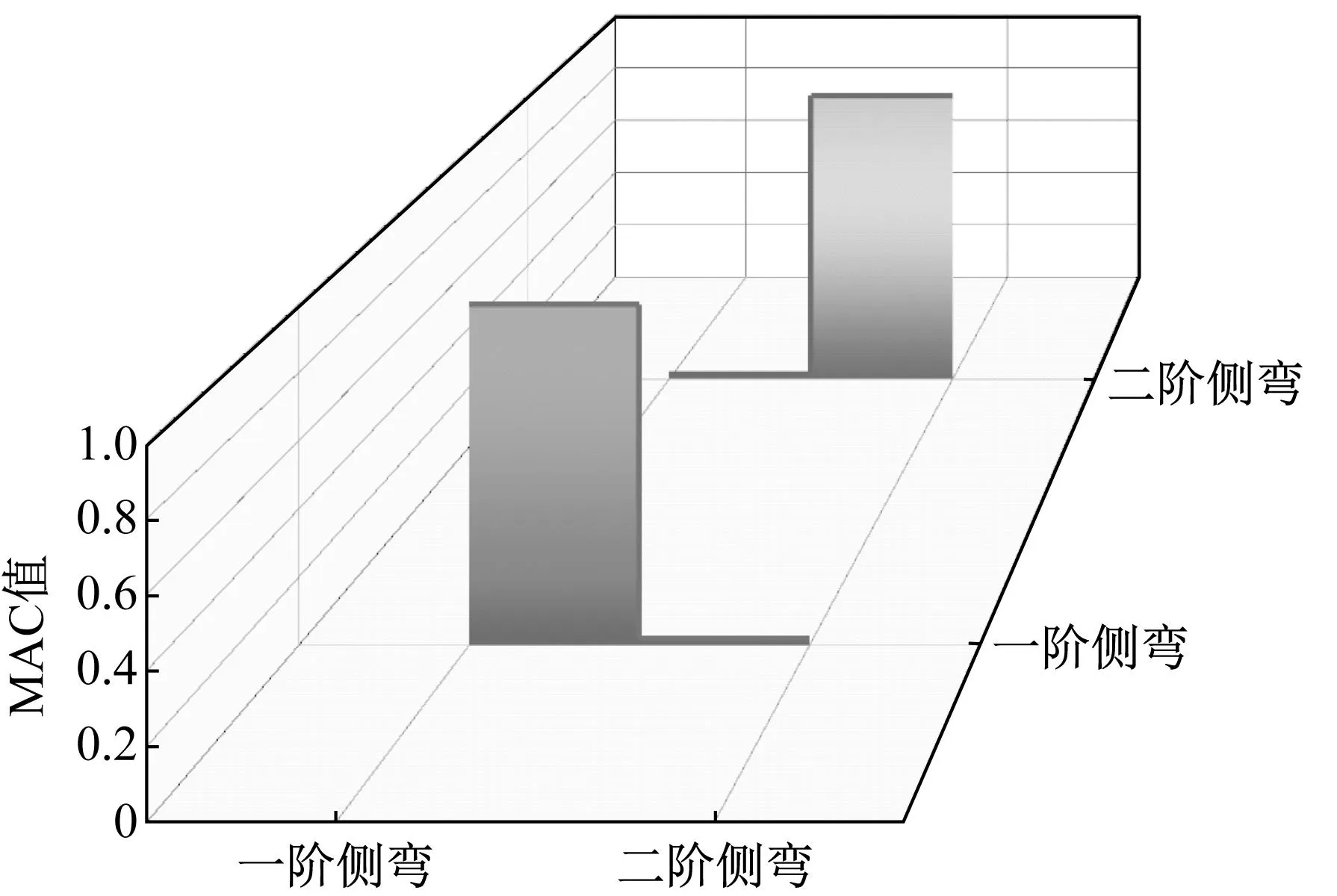
(b) 前八阶横向模态MAC值图形图16 前八阶模态理论振动与实测振动MAC值图形Fig.16 Graph of MAC values for theoretical and measured vibrations of the first eight modes

从静力、动力特征的模拟结果可以得出,基于RBFNN-ISSA的有限元模型修正方法对于大跨径悬索桥有限元模型的修正具有良好的适用性,有效改善了结构有限元模型模拟失真的情况,验证了该有限元模型修正方法的可行性。

6 结 论

针对大跨径悬索桥结构有限元模型修正精度不高、效率低问题,提出了径向基神经网络子结构代理模型与混合策略改进麻雀搜索算法的有限元模型修正方法。该方法基于桥梁响应测试数据建立以模型静、动力特性误差为目标函数的有限元参数修正的数学模型,通过径向基神经网络代理模型与改进麻雀搜索算法进行交互,避免了传统有限元模型庞大的计算成本。以杭瑞高速洞庭湖大桥实测数据为依托,在两个静力加载工况和模态测试结果支撑下验证了该有限元修正方法的有效性与泛化能力。结果表明,本文方法在精度、效率与可靠性上具有明显提升,可应用于类似复杂工程的模型修正。具体结论如下:

(1) 对于大跨径悬索桥一类的大型复杂工程,在进行有限元模型修正时,采用子结构模拟的方法将整体结构以子单元形式进行解构重组,可以同步提升模型修正精度和整体结构修正时的迭代计算效率。

(2) 提出的RBFNN-ISSA的有限元模型修正方法对于大跨径悬索桥有限元模型修正问题具有良好的适用性,修正后模型在静力、动力特征的模拟精度均远高于初始有限元模型。实验发现,两级加载工况下主梁挠度平均相对误差降低约25%以上,模态频率平均相对误差修正后也由-6.83%降至了-2.38%,MAC值结果表明修正后的有限元模型能够准确反映出桥梁的实际振动状态,有效改善了初始模型模拟失真的问题,实现了有限元模型的合理精准修正;

(3) 融合Tent混沌映射、黄金正弦和柯西变异策略改进的麻雀搜索算法(ISSA),相较于标准麻雀搜索算法(SSA)在收敛速度与稳定性上也有较大优势。在杭瑞高速洞庭湖大桥有限元模型参数寻优的实际问题中,ISSA仅在90代左右即收敛至全局最优解,而SSA算法种群未能摆脱局部极值的干扰,说明本文提出的复杂结构模型修正方法具有良好的可靠性;

(4) 基于径向基神经网络的子结构代理模型对结构材料参数与静、动力响应之间的非线性映射关系拟合良好,50个检验点的残差平方和仅为5.11×10-4,复相关系数的平方R2为0.979 4,具有较强的学习泛化能力,未来可研究应用于类似复杂结构工程代理模型的建立。